Restless Multi-Armed Bandits (RMABs) are a powerful framework for sequential decision-making, widely applied in resource allocation and intervention optimization challenges in public health. However, traditional RMABs assume independence among arms, limiting their ability to account for interactions between individuals that can be common and significant in a real-world environment. This paper introduces Networked RMAB, a novel framework that integrates the RMAB model with the independent cascade model to capture interactions between arms in networked environments. We define the Bellman equation for networked RMAB and present its computational challenge due to exponentially large action and state spaces. To resolve the computational challenge, we establish the submodularity of Bellman equation and apply the hill-climbing algorithm to achieve a $1-\frac{1}{e}$ approximation guarantee in Bellman updates. Lastly, we prove that the approximate Bellman updates are guaranteed to converge by a modified contraction analysis. We experimentally verify these results by developing an efficient Q-learning algorithm tailored to the networked setting. Experimental results on real-world graph data demonstrate that our Q-learning approach outperforms both $k$-step look-ahead and network-blind approaches, highlighting the importance of capturing and leveraging network effects where they exist.
Public health challenges such as infectious disease control, vaccination strategies, and chronic illness management require sophisticated sequential decision-making under uncertainty, where timely decisions can significantly impact population health outcomes [World Health Organization, 2019]. The Restless Multi-Armed Bandit (RMAB) framework has emerged as a powerful tool for addressing such sequential decision-making problems under resource constraints. Prior work has successfully applied variations of RMABs to various public health settings, such as optimizing treatment strategies for infectious diseases [Mate et al., 2020], designing treatment policies for tuberculosis patients [Mate et al., 2021], efficient streaming-patient intervention planning [Mate et al., 2022], and fair resource allocation across patient cohorts [Li and Varakantham, 2022].
However, a significant limitation of traditional RMAB models is the assumption of independence among arms. In many public health applications, the state of one individual directly affects others due to network effects. For example, in epidemic processes infection propagates along contact networks, so an individual’s health status changes the risk faced by their neighbors [Pastor-Satorras and Vespignani, 2001, Wang et al., 2003, Pastor-Satorras et al., 2015, Kiss et al., 2017]. During the COVID-19 pandemic, the impact of interventions such as vaccination or quarantine depended not only on who was targeted but also on the topology of the underlying interaction graph [World Health Organization, 2020, Funk et al., 2010]. Ignoring such dependencies can yield sub-optimal resource allocation, higher transmission rates, and increased morbidity. To model such interactions, the Independent Cascade (IC) model has been widely used to capture the probabilistic spread of influence through a network [Kempe et al., 2003].
Our work introduces the Networked Restless Multi-Armed Bandit (NRMAB) framework, which integrates the RMAB model with the Independent Cascade model to account for network effects. This enables more realistic representations of how interventions on one individual can influence the health states of others. By incorporating network effects, our model allows the action on one arm to influence not only its own state transitions but also those of neighboring arms through cascades.
We formulate Bellman’s equation for this networked problem and prove that the value function is submodular. Because activation is probabilistic and arms can passively change states, traditional submodularity proofs for independent cascade no longer work [Kempe et al., 2003].We adapt the original proof to this setting, accommodating probabilistic activation and passive state changes. Submodularity in turn unlocks a greedy hill-climbing action-selection policy for Bellman equation whose return is at least (1 -1/e) of the optimal [Nemhauser et al., 1978].
We then establish that the Bellman operator with hill-climbing action selection is a γ-contraction. Because greedy selection can be sub-optimal, classical contraction proofs that rely on optimal action selection no longer apply. We design an equivalent multi-bellman operator with a meta-MDP and show this operator contracts under the supremum norm [Carvalho et al., 2023]. Value iteration converges linearly, and finite-horizon implementations inherit tight error bounds, ensuring practical algorithms remain stable and sample-efficient.
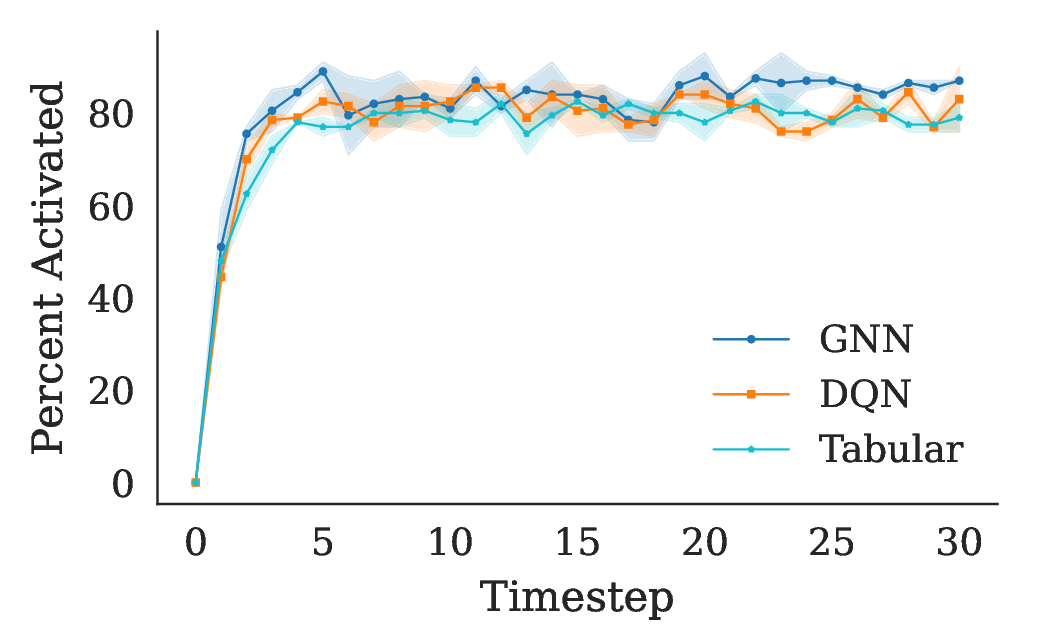
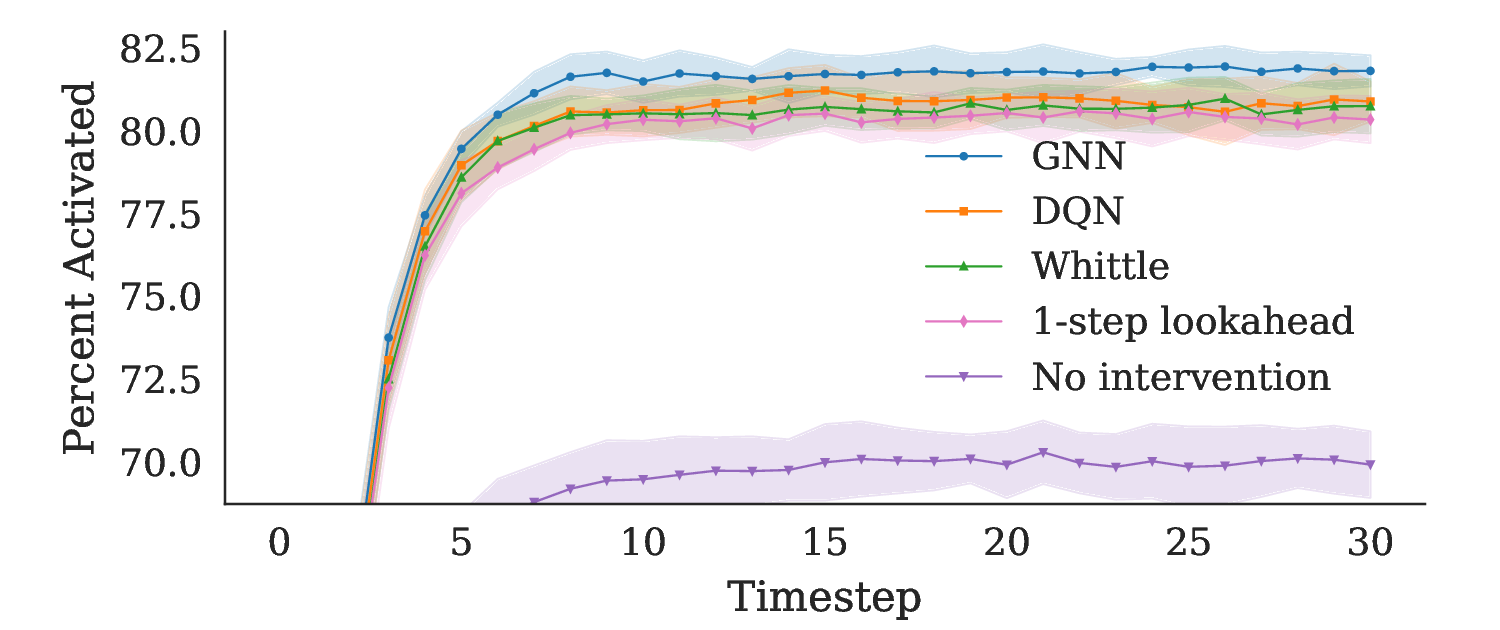
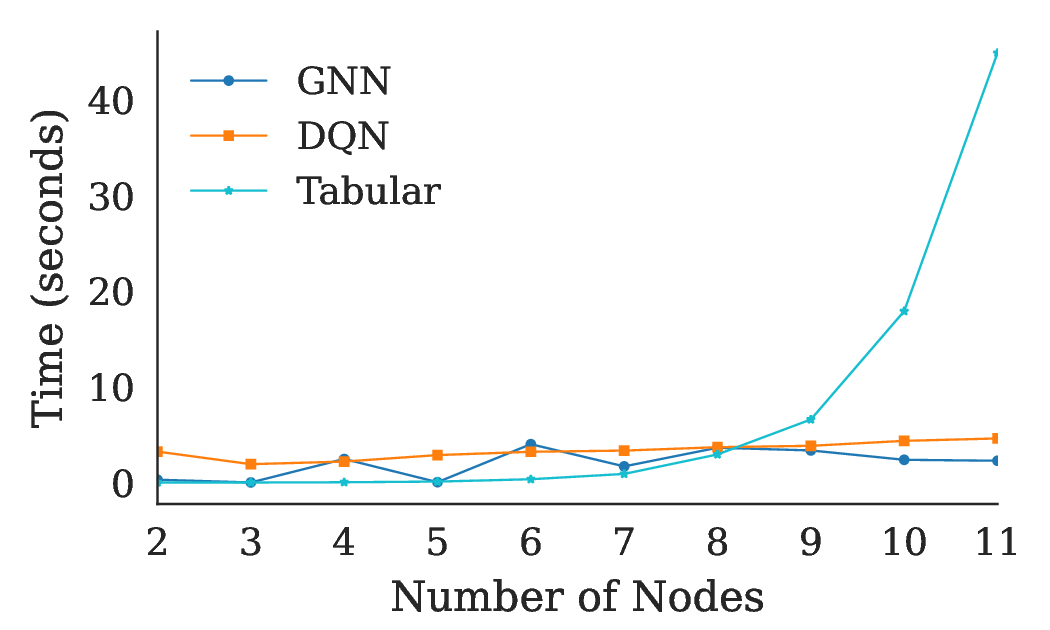
Building on this theoretical foundation, we develop a Q-learning algorithm for NRMABs. Our algorithm uses hillclimbing action selection for the Bellman equation to approximate the optimal policy without the need to compute the exact value function, which is computationally infeasible in large networks. We validate our approach through experiments on synthetic networks, demonstrating that our network-aware algorithm outperforms network-blind baselines, including the traditional Whittle Index policy [Whittle, 1988]. These results highlight the importance of capturing network effects in sequential decision-making problems and suggest that NRMABs can provide more effective intervention strategies in public health and other domains where networked interactions are significant.
Restless multi-armed bandits RMABs, first introduced by Whittle [1988], extend the classic Multi-Armed Bandit framework to scenarios where each arm evolves over time regardless of whether it is selected, making a powerful model for decision-making problems in uncertain and evolving environments. Finding optimal policies for RMABs is PSPACEhard [Papadimitriou and Tsitsiklis, 1999], leading to the development of various approximation algorithms, such as the Whittle index policy [Whittle, 1988]. RMABs have been applied in domains such as machine maintenance [Glazebrook et al., 2005], healthcare [Mate et al., 2020], and communication systems [Liu and Zhao, 2010].
The Independent Cascade model, introduced by Kempe et al. [2003], captures the pr
This content is AI-processed based on open access ArXiv data.