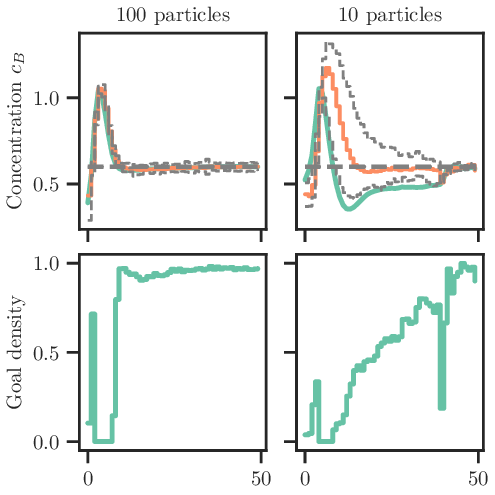
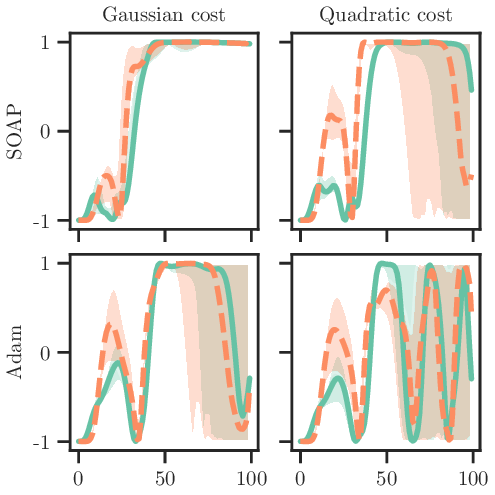
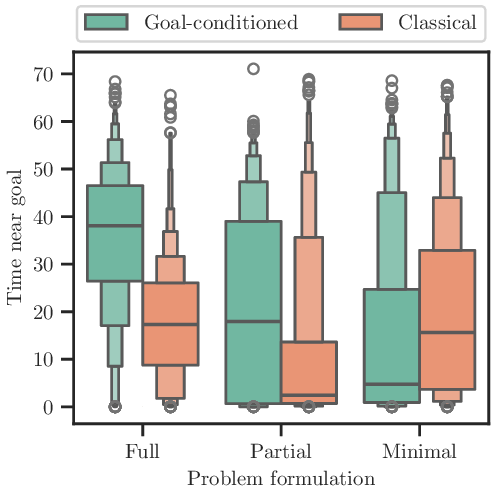
Goal-conditioned reinforcement learning (RL) concerns the problem of training an agent to maximize the probability of reaching target goal states. This paper presents an analysis of the goal-conditioned setting based on optimal control. In particular, we derive an optimality gap between more classical, often quadratic, objectives and the goal-conditioned reward, elucidating the success of goal-conditioned RL and why classical ``dense'' rewards can falter. We then consider the partially observed Markov decision setting and connect state estimation to our probabilistic reward, further making the goal-conditioned reward well suited to dual control problems. The advantages of goal-conditioned policies are validated on nonlinear and uncertain environments using both RL and predictive control techniques.
Dynamic programming is at the heart of optimal decisionmaking under uncertainty, giving general optimality conditions for an agent to satisfy (Bertsekas, 2012). Traditionally, the optimal control problem consists of two distinct objects: a reward and an uncertain model. This paper sits in the general setting of dynamic programming, but reexamines the role of the reward function. In particular, we leverage the dynamic uncertainty to not only estimate the hidden state, but also the probability of reaching target states. This results in a dual control problem in which the objective is an "intrinsic" quantity that directly stems from the system uncertainty.
The notion of a probabilistic reward function has been proposed in the goal-conditioned reinforcement learning (RL) literature (Eysenbach et al., 2022), and has connections to indicator-type rewards (Eysenbach et al., 2021;Liu et al., 2022;Lawrence et al., 2025). However, solution methods by Eysenbach et al. (2021Eysenbach et al. ( , 2022) ) are indirect, employing contrastive learning techniques for learning policies. This is because direct approaches may be intractable either due to lack of model knowledge or sparsity of the probabilistic reward function. Meanwhile, classic control typically uses a quadratic cost to formulate optimal control problems; in the RL literature these are so-called “dense” rewards. While such rewards are not sparse, they can still be difficult to configure towards good performance, making them nuisance parameters in goal-reaching tasks.
Despite strong evidence that goal-oriented rewards are effective for solving complex control tasks, it is unclear ⋆ This work has been submitted to IFAC for possible publication. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences under award number DE-SC0024472. why this is the case, or more precisely, why there is a significant performance gap between dense and probabilistic rewards. This paper sheds light on probabilistic rewards from the vantage point of classic optimal control. We take a direct, value-based approach towards analyzing the goaloriented objective. More specifically, our contributions are summarized as follows:
(1) An inequality that directly lower bounds the objective of goal-oriented policies in terms of “classical” formulations, corroborating folklore that dense rewards may not be suitable for goal-oriented planning (Section 3.1). (2) Extension to the partially observed setting in which we draw connections to dual control. In this setting, the reward itself is intimately tied to state estimation, yielding a control problem defined entirely by system uncertainty (Section 3.2). (3) Case studies in challenging nonlinear and uncertain environments where we employ a broad range of techniques (Section 4), emphasizing that the above benefits are related to the control objective itself and not necessarily the underlying algorithms (Section 5).
Similarly, we show how the same methods but with classical objective functions can falter.
The crux of this paper is captured in the distinction between the following two control objectives:
Objectives of the former style are referred to as classic control. The inner term is a familiar quadratic cost, while the exponentiation relates the costs to probabilities, leading to maximum-entropy (Levine, 2018), dual (Todorov, 2008), and robust (Jacobson, 1973) control formulations. We will refer to the latter objective as goal-oriented.
The goal-oriented objective is motivated as follows. An idealized reward for goal-directed behavior would be of an indicator type, providing positive feedback only when a goal state is achieved. However, such feedback is vanishingly sparse, as in a continuous and stochastic environment a learning agent will never reach the precise goal (with probability one). Instead, the goal-oriented objective can be seen as a sum of (unnormalized) probability densities around the origin:
1 Goal is achieved 0 Otherwise where ϵ > 0 is made arbitrarily small. Indicator type objectives with tunable tolerance ϵ are common in RL (Liu et al., 2022). Instead, this paper focuses on a goal-oriented framework with the density structure outlined above, as it reflects the intrinsic uncertainty of the environment, meaning it is the “true” objective, while the indicator type objective is an idealized representation.
To see the difference between the classical and goaloriented objectives, suppose the initial state is far from the origin, but the agent reaches its goal in T time steps. Then, the classic control objective becomes degenerate, as exp(-
depending entirely on the initial state. In contrast, the goal-oriented objective is approximately γ T /1-γ, depending entirely on T . This simple example indicates that the classic control objective (which uses a so-called “dense” reward) is sparse in the initial state space, whereas the goal-oriented objective is spars
This content is AI-processed based on open access ArXiv data.