Knot theory is an active field of mathematics, in which combinatorial and computational methods play an important role. One side of computational knot theory, that has gained interest in recent years, both for complexity analysis and practical algorithms, is quantum topology and the computation of topological invariants issued from the theory.
In this article, we leverage the rigidity brought by the representation-theoretic origins of the quantum invariants for algorithmic purposes. We do so by exploiting braids and the algebraic properties of the braid group to describe, analyze, and implement a fast algorithm to compute the Hecke representation of the braid group. We apply this construction to design a parameterized algorithm to compute the HOMFLY-PT polynomial of knots, and demonstrate its interest experimentally. Finally, we combine our fast Hecke representation algorithm with Garside theory, to implement a reservoir sampling search and find non-trivial braids with trivial Hecke representations with coefficients in $\mathbb{Z}/p\mathbb{Z}$. We find several such braids, in particular proving that the Hecke representation of $B_5$ with $\mathbb{Z}/2\mathbb{Z}$ coefficients is non-faithful, a previously unknown fact.
Geometrically, a braid on n strands is the embedding of n non-intersecting paths in the 3-dimensional space R 2 × [0, 1], such that every path connects a point (i, 0, 0), i ∈ {1, . . . , n} in the bottom plane to a point (j, 0, 1), j ∈ {1, . . . , n} in the top plane, and every path grows monotonically along the z-axis. Two braids are equivalent if there is an ambient isotopy of R 2 × [0, 1] fixing the bottom and top planes and taking one braid to the other. Braids are generally represented by braid diagrams, that are planar projections of a braid along the y-axis, keeping track of upper and under crossings; see Figure 1.
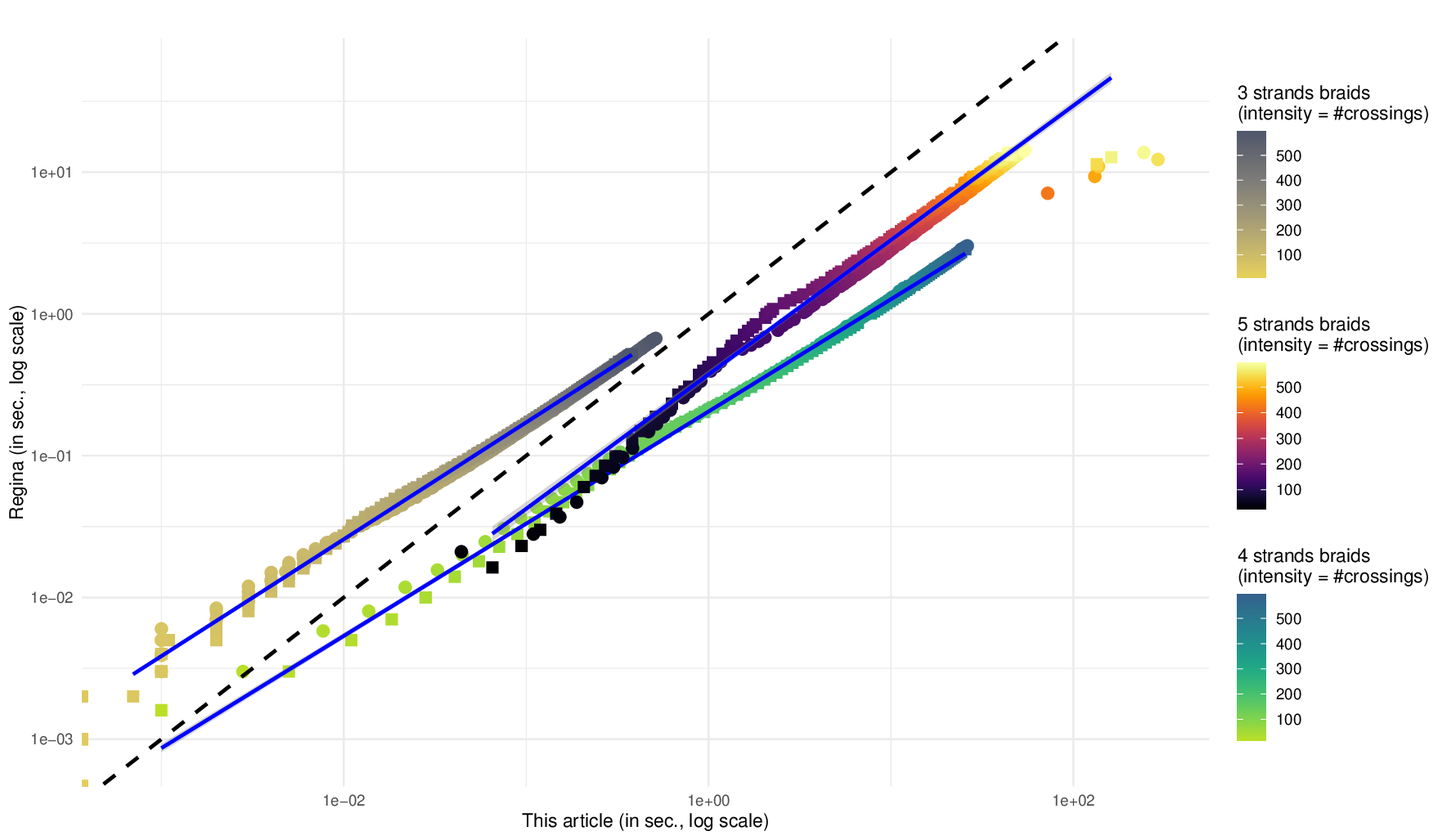
Braids are notably important in knot theory, as any link can be represented as the closure of a braid [1]. Knots have been studied extensively under the algorithmic lens. A famous problem is the computational complexity of recognizing the trivial knot from an input diagram, which is known to be in the complexity classes NP [20] and coNP [27], for which the best known worst case algorithm is exponential [20], but which experimentally exhibits a fast polynomial time behavior [12] with optimized implementation. In particular, the experimental aspects of computational knot theory play a fundamental role in the field, where mathematicians and computer scientists use efficient software, such as Regina [7,10] and SnapPy [13], as well as computer-constructed census of knots [9], to guess and challenge profound conjectures, e.g. [6,15,17]. Consequently, an important side of computational knot theory is the design and implementation of fast, highly optimized algorithms.
Motivated by a finer understanding of the complexity of problems related to knots as well as practically fast computation, a recent route of research uses tools from parameterized complexity to compute topological invariants of knots. This approach has been particularly successful for invariants constructed via quantum topology, a field of topology using tools from quantum mechanics. In particular, the treewidth of a graph is a parameter measuring how close the graph is to a tree and, similarly, the pathwidth measures the proximity to a path. They can be extended to knot theory by considering the graph obtained from a diagram by putting a vertex on each crossing and an edge for each strand connecting crossings.
These are important parameters capturing a certain notion of sparsity of the input, and they can be combined with algorithmic techniques such as dynamic programming to design algorithms whose complexity depends exponentially on the tree/pathwidth and only polynomially in the size of the input: in quantum topology, such algorithms have been designed for the Jones and Kauffman polynomials [30], the Reshetikhin-Turaev invariants [31], and the HOMFLY-PT polynomial [8], which are #P-hard to compute in general [26]. Note that these quantum invariants, together with theoretically and practically fast algorithms, have been applied to construct knot censuses [9].
Contrary to knots, braids on n-strands have a natural algebraic description as a group, the braid group B n , yielding rich algebraic properties. To our knowledge, braids have not received the same attention from the computer science community compared to knots.
Our results. The goal of this article is to describe fast algorithms and data structures for braids and the braid group, related to quantum topology, and to apply them to computational knot theory and experimental mathematics. As opposed to algorithms on knots mentioned above, these algorithms rely heavily on the algebraic structure of the braid group.
Our starting point is to consider the Hecke representation of a braid. The Hecke algebra H n is a fundamental concept in modern mathematics [32], deeply connected to group theory, number theory, and knot theory. The braid group B n admits a representation into the Hecke algebra H n , i.e., a map B n → H respecting the group structure. Knowing whether this map (with Z-coefficients) is faithful (i.e., only the trivial braid has trivial image) is a major open question [37,23,28,5], related to the detection of the unknot by the Jones polynomial [21].
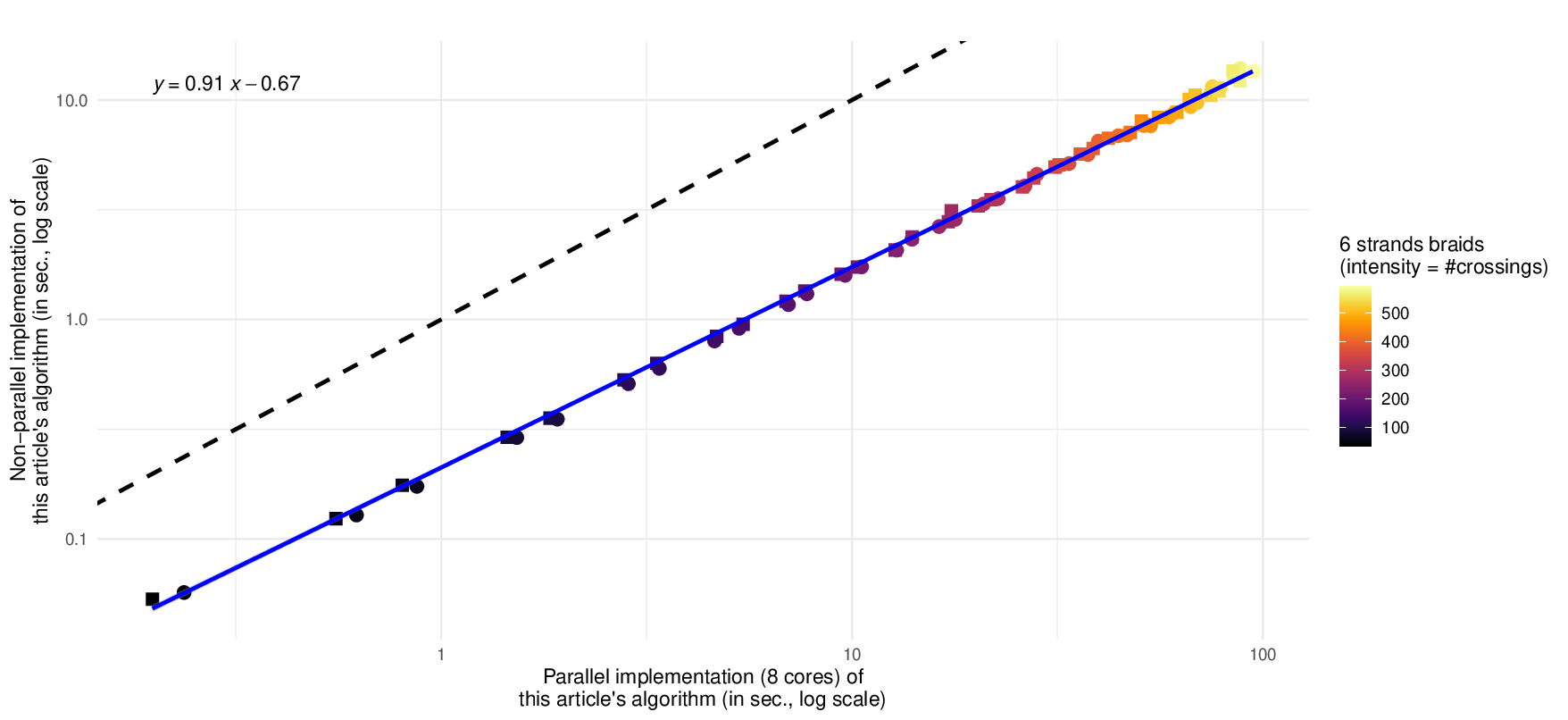
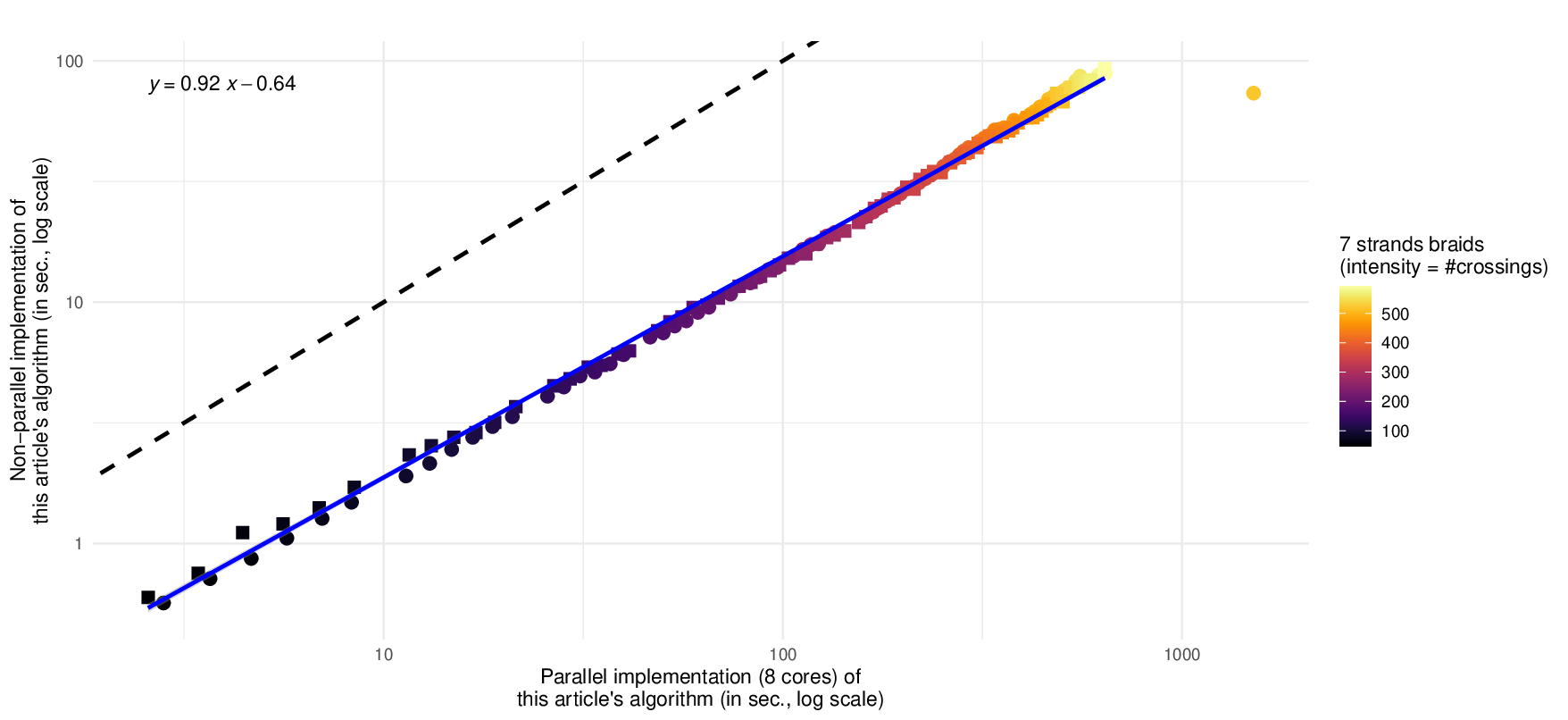
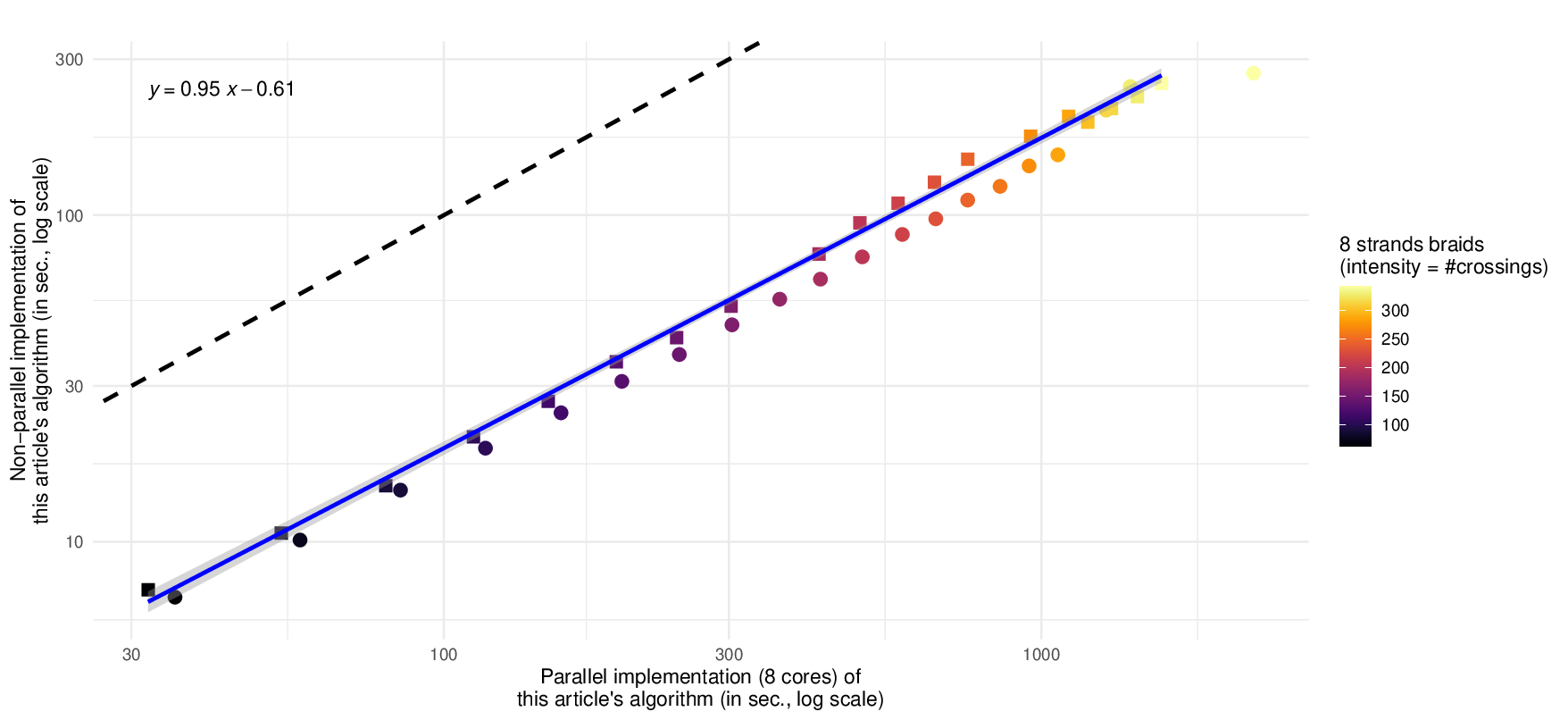
Our algorithm consists of scanning an input braid diagram from bottom to top, and updating the representation of the braid in a basis of H. This natural strategy of computation has already been used by Hugh Morton in 1985 [33]; the program that results from our work can be seen as a modern and optimized implementation of Morton’s high level ideas.
▶ Theorem 1 (see Theorem 11). Given a braid b ∈ B n on n strands and with N crossings, there is an algorithm to compute its Hecke representation in O(n!(n log n) × N ) operations and O(n! × N ) algebraic operations, storing n! + O(1) algebraic elements.
Every knot or link can be obtained from the braid closure of a braid [1]; see Figure 1. Additionally, the HOMFLY-PT polynomial of the knot/link obtained from the braid closure can be computed from the Hecke representation of th
This content is AI-processed based on open access ArXiv data.