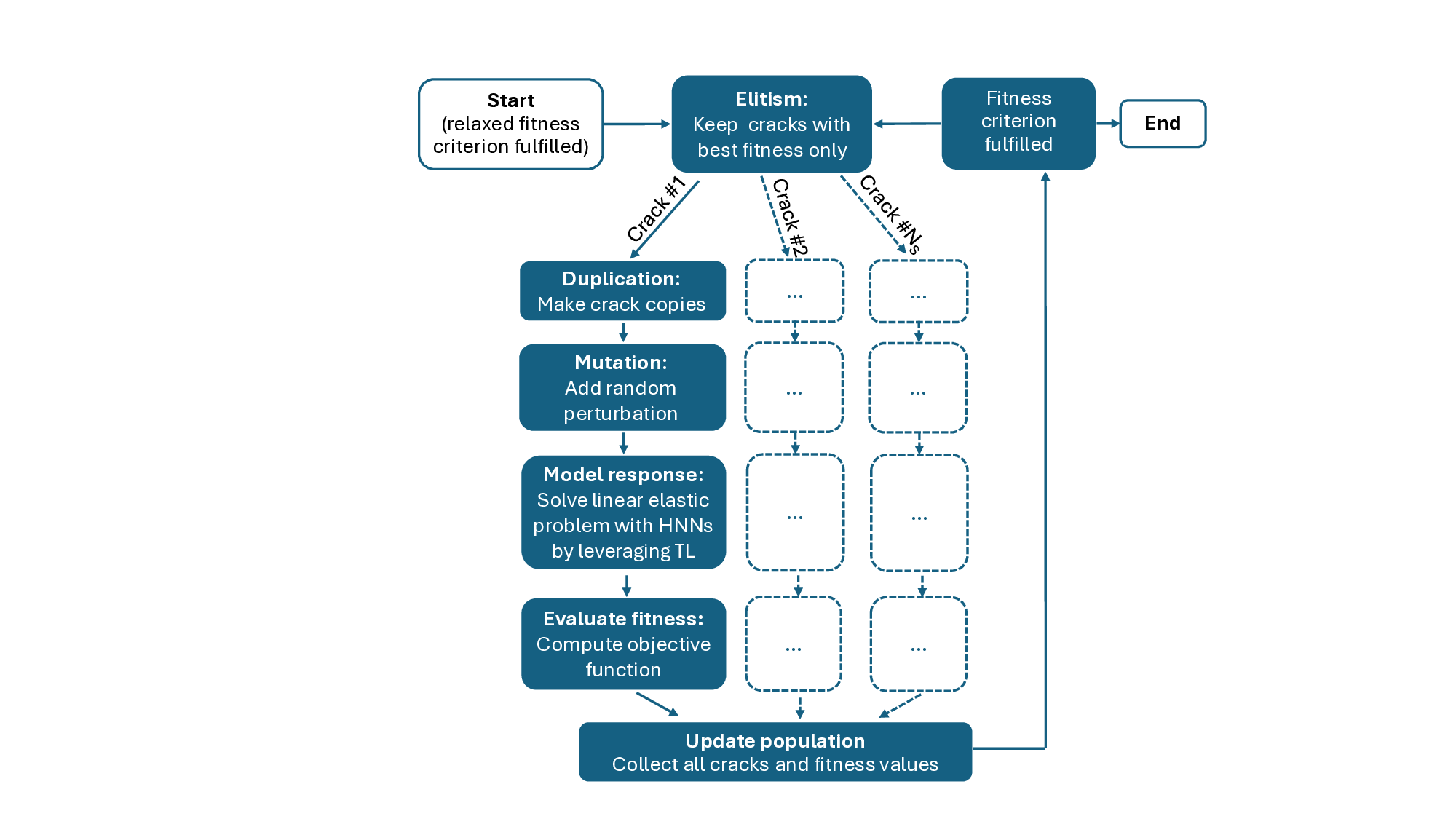
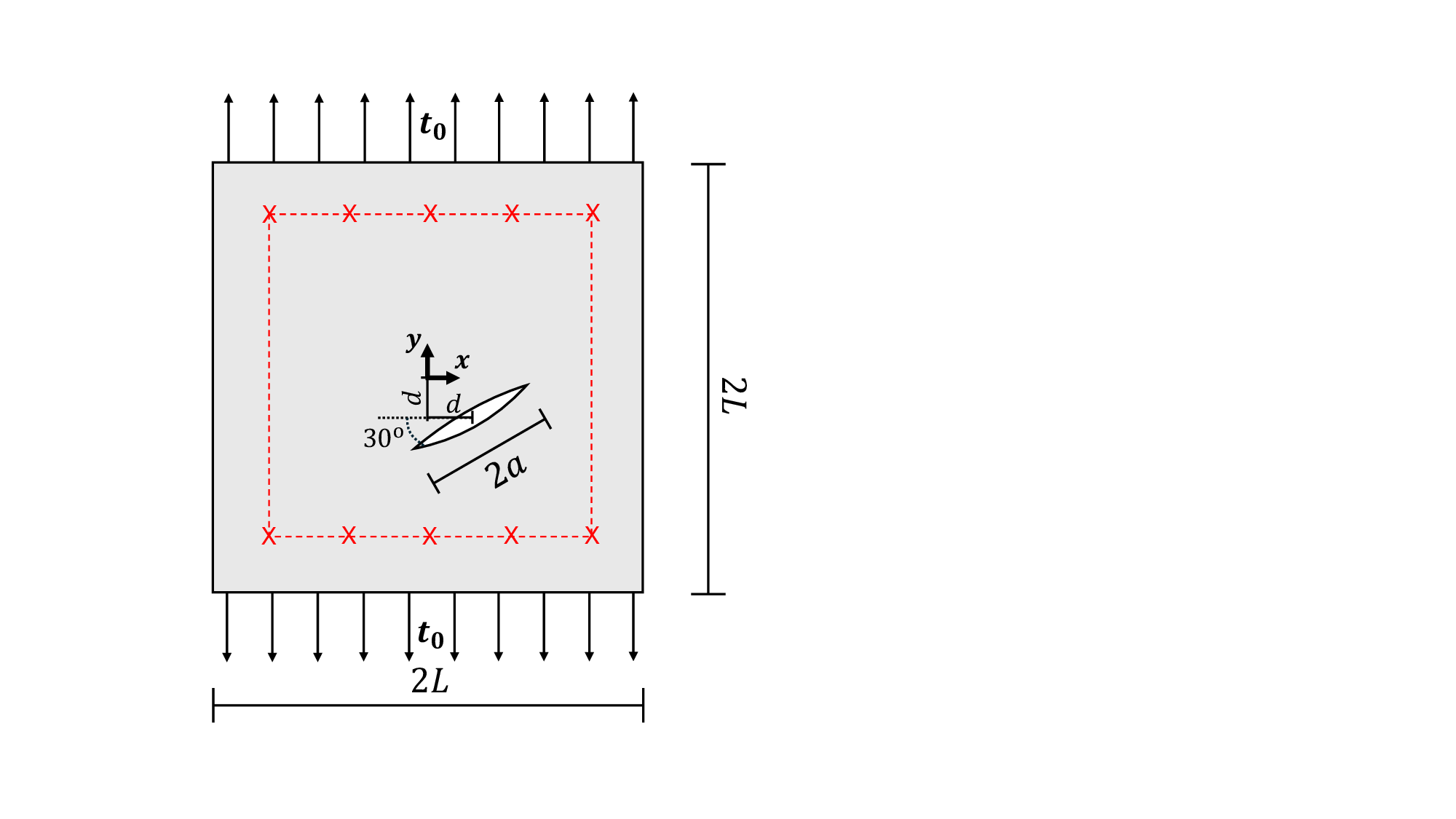
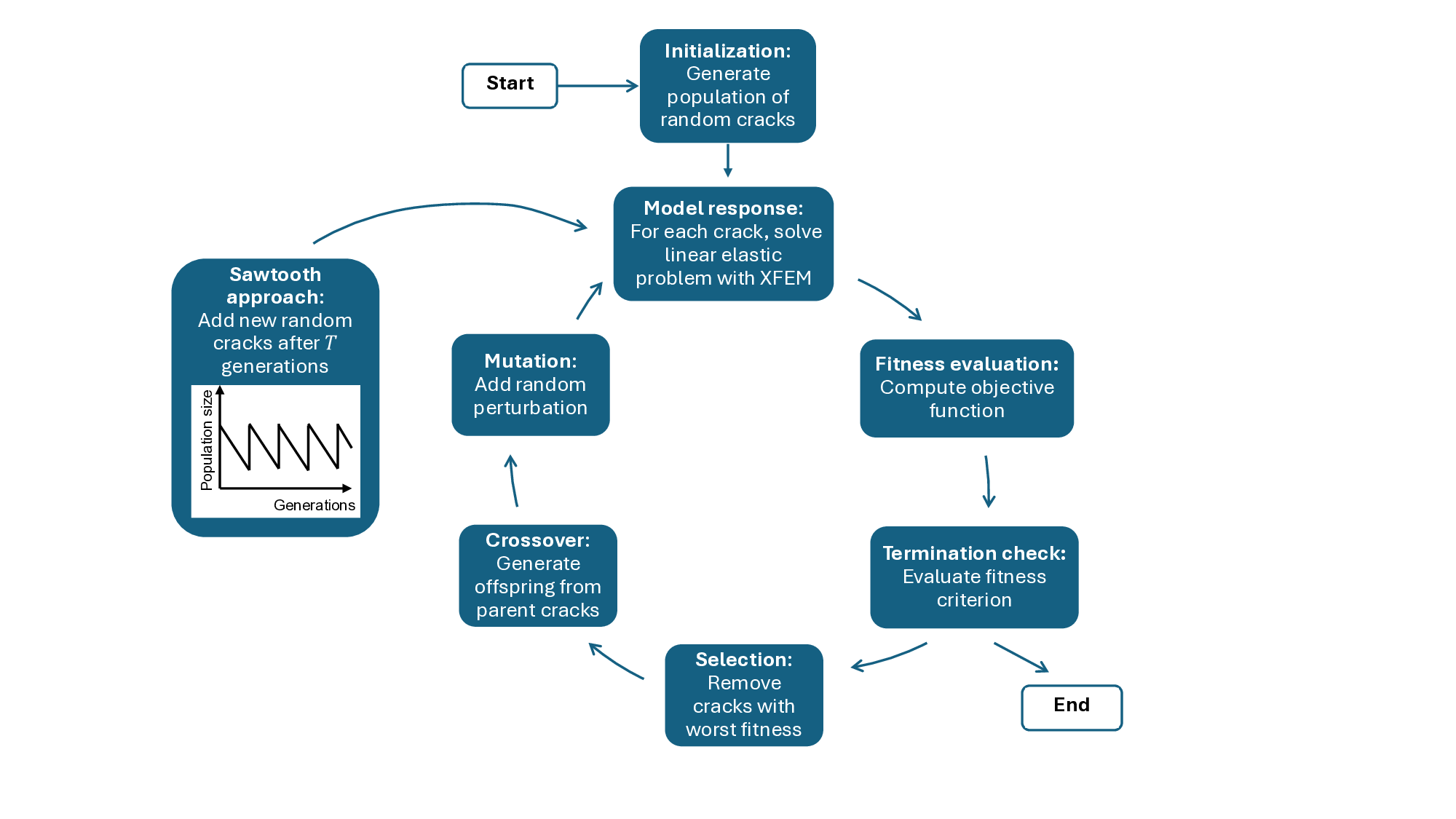
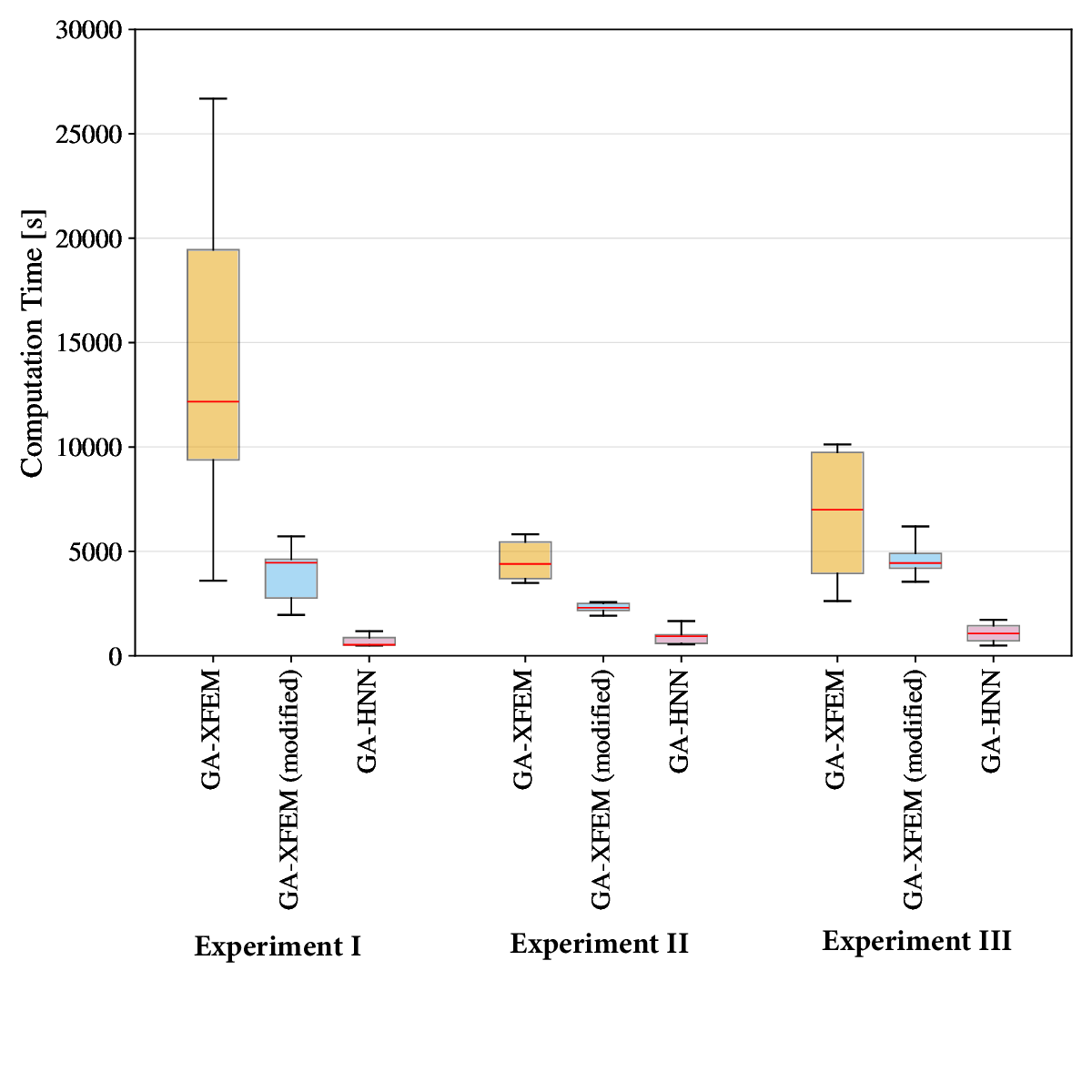
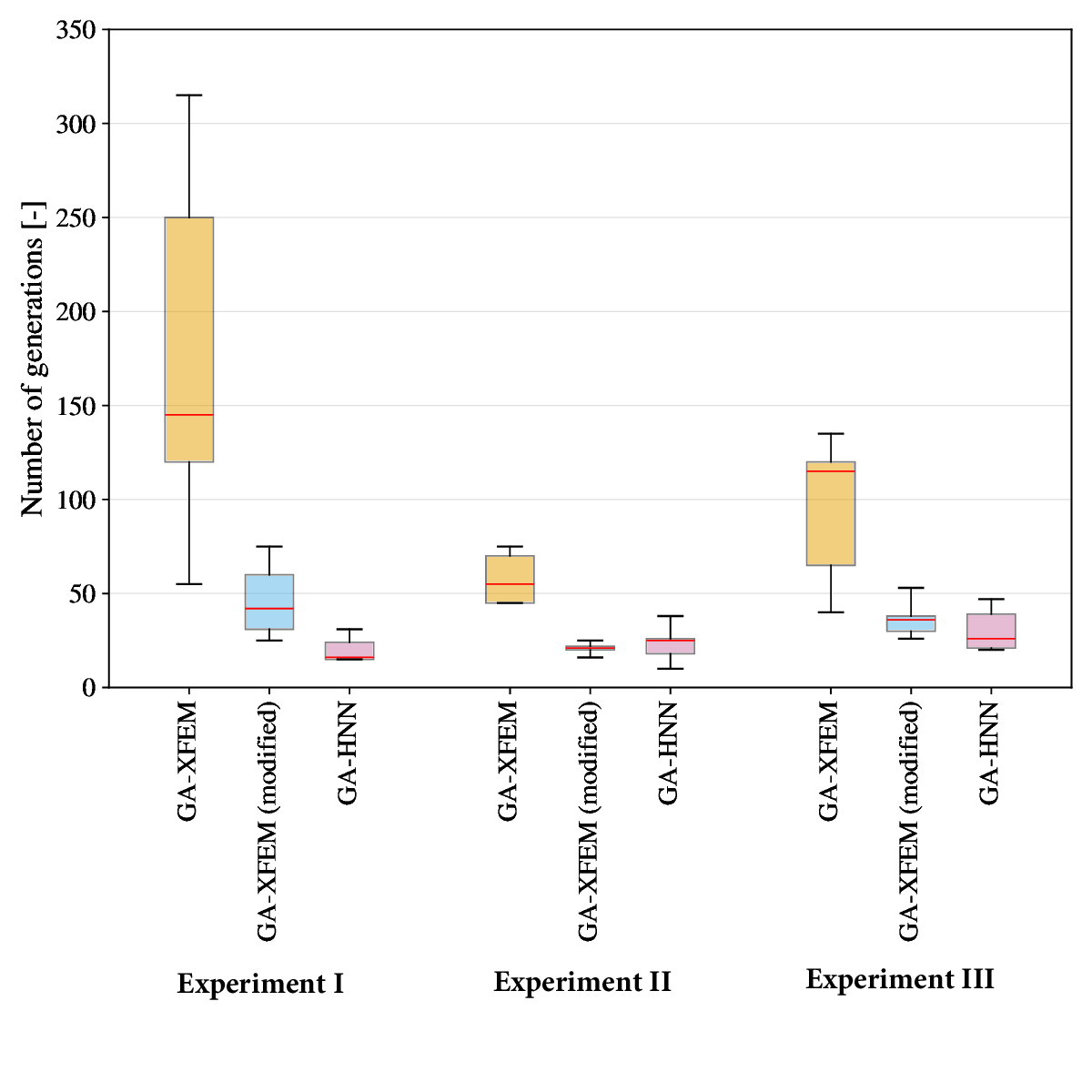
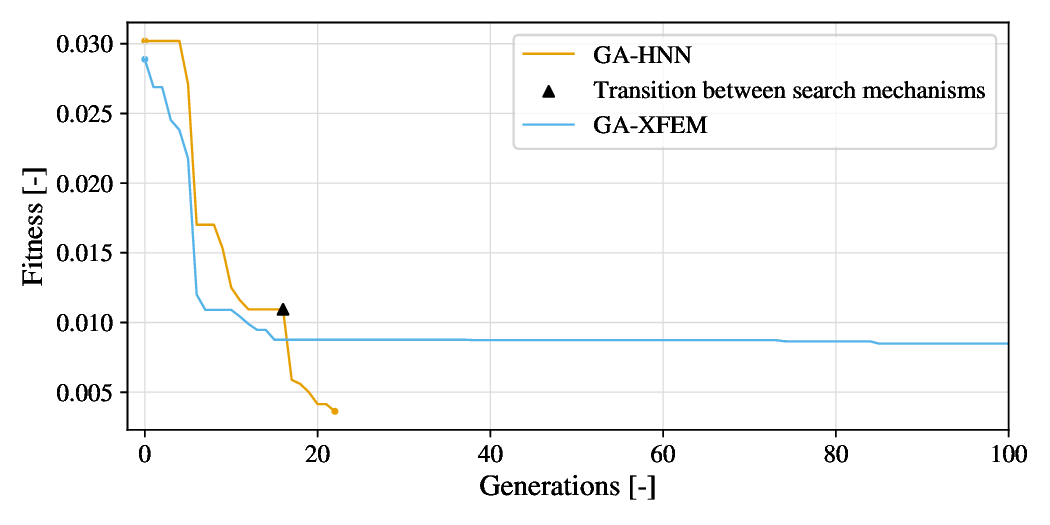
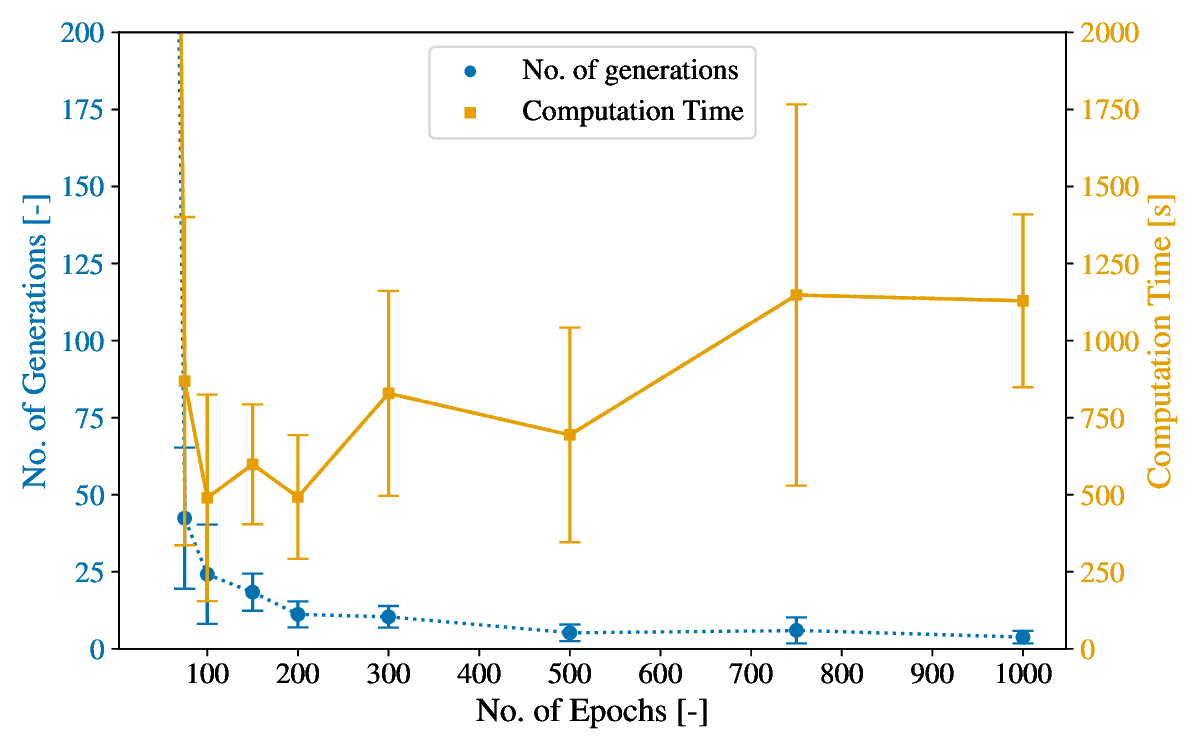
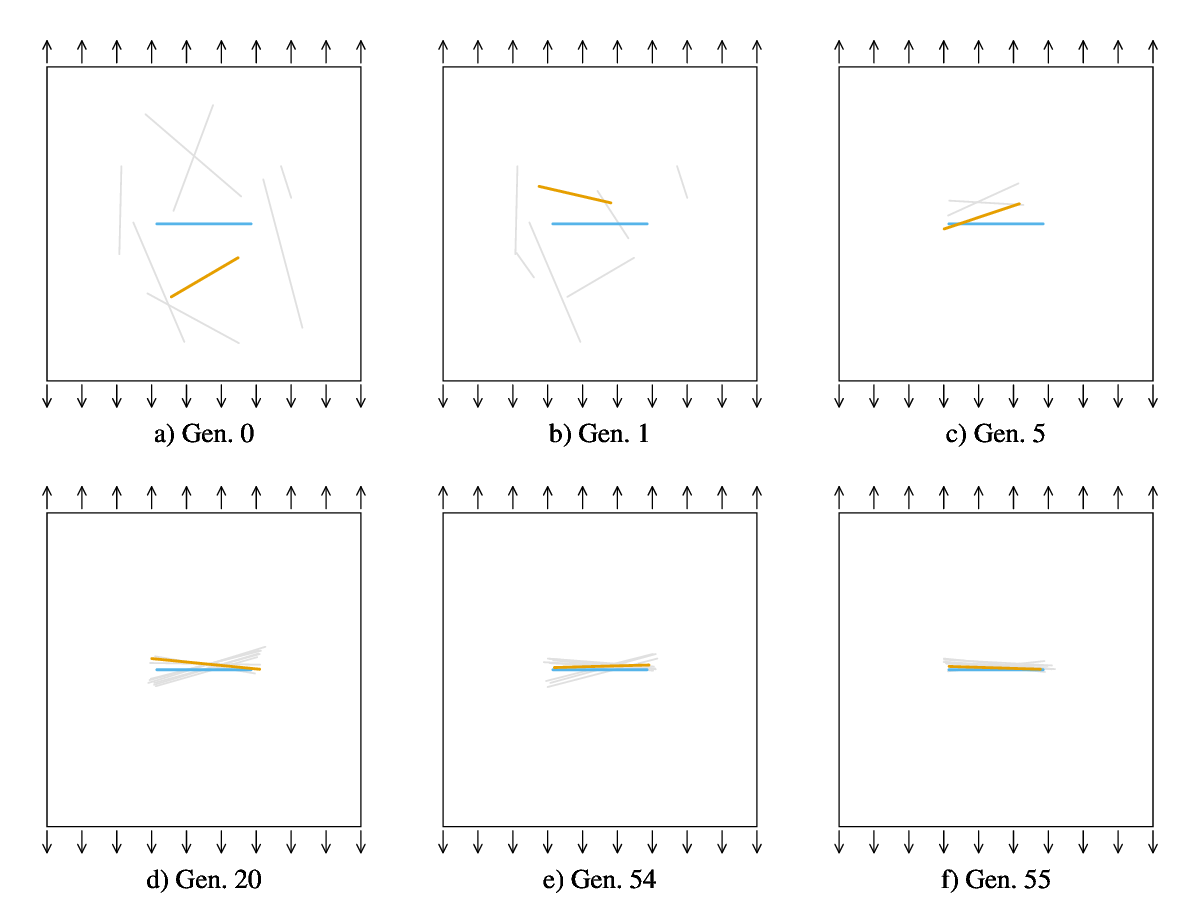
A new strategy for detecting cracks in 2D solids based on strain data is introduced. Crack detection is formulated as an inverse problem and solved using genetic optimization. The novelty lies in the evaluation of the model response at each generation. Specifically, the solution to the corresponding plane elasticity problem is expressed via holomorphic potentials, which are determined by training two holomorphic neural networks. As the potentials satisfy equilibrium and traction-free conditions along the crack faces a priori, the training proceeds quickly based solely on boundary information. Training efficiency is further improved by splitting the genetic search into long-range and short-range stages, enabling the use of transfer learning in the latter. The new strategy is tested on three benchmark problems, showing that an optimal number of training epochs exists that provides the best overall performance. A comparison is also made with a popular crack detection approach that uses XFEM to compute the model response. Under the assumption of identical stress-field representation accuracy, the proposed method is found to be between 7 and 23 times faster than the XFEM-based approach. While the strategy is presented here for the simplified case of a single internal crack, generalization is feasible. Overall, the present findings demonstrate that combining genetic optimization with holomorphic neural networks and transfer learning offers a promising avenue for developing crack detection strategies with higher efficiency than those currently available.
The capability to detect, locate, and evaluate damage or degradation in structures to ensure their reliability and performance throughout their service life is crucial for modern society. In this context, research on structural health monitoring has received considerable attention over the past decades [1].
Structural health monitoring can be defined as the assessment of a structure’s condition through integrated sensing, data acquisition, and analysis techniques [2,3]. Several well-established sensing methodologies are now available to detect early signs of degradation, predict structural failures, and ensure overall safety. These include temperature sensing, electrical and electrochemical sensing, local strain measurement, ultrasonic testing, automated visual inspection, vibration-based methods, and acoustic emission techniques [4]. Based on the recorded signals, damage detection is typically conducted either using a reference model of the structure (physics-based approaches) or through signal-processing-based techniques (data-driven approaches) [1].
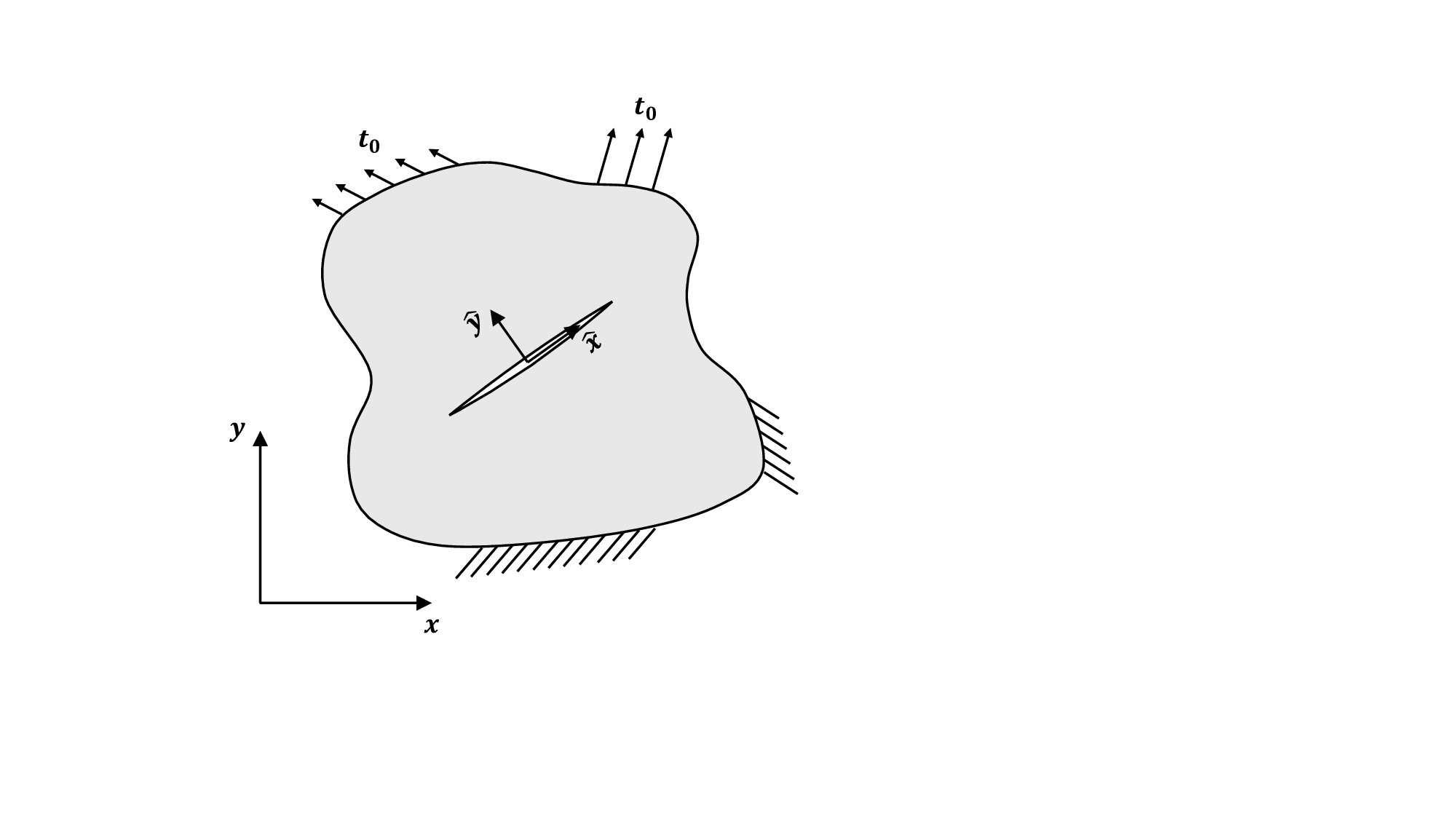
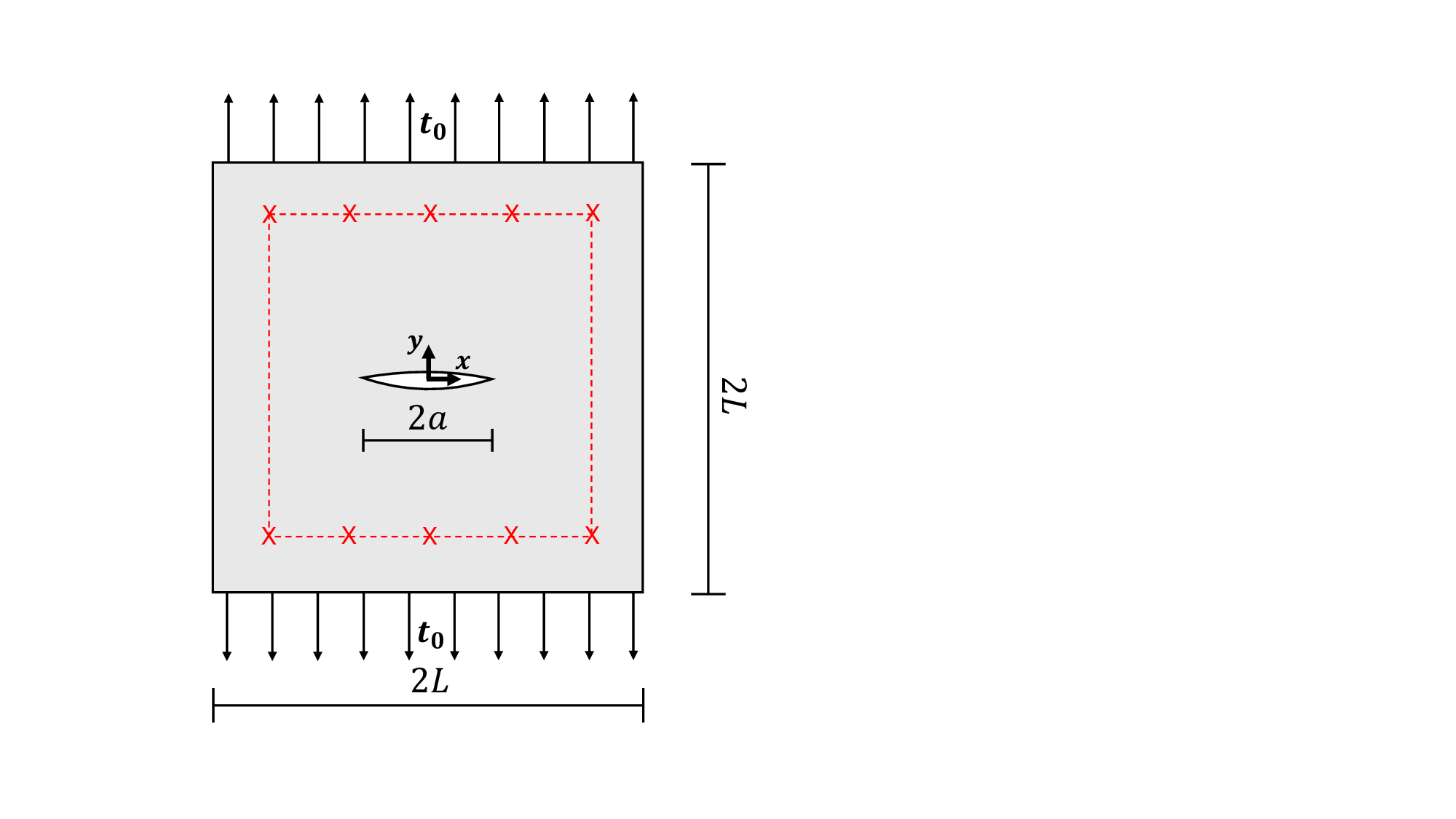
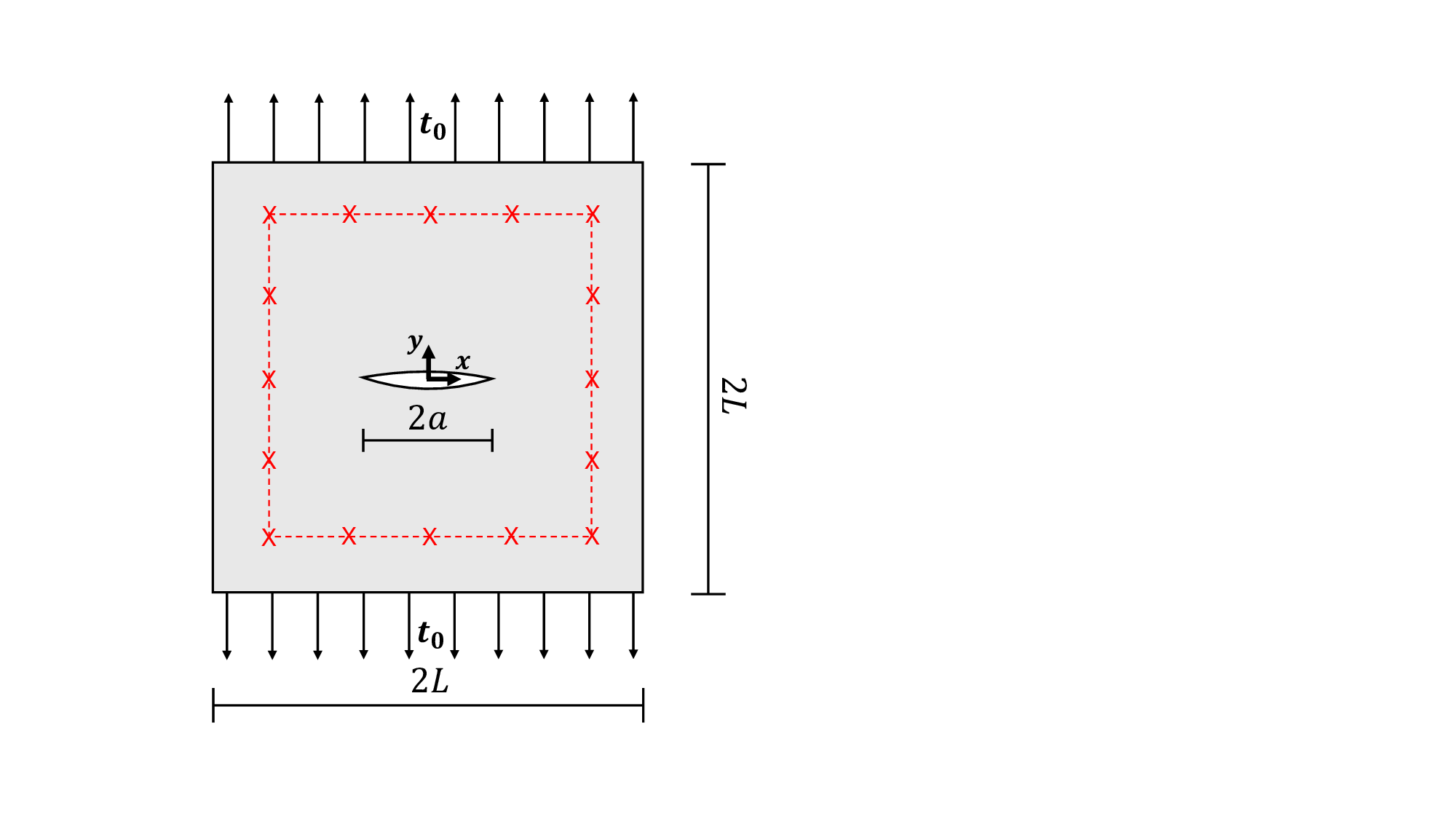
In physics-based approaches, damage is detected via an inverse procedure that aims to minimize the discrepancies between the model response and the sensor data [5]. In the specific case of crack detection based on strain measurements, this procedure is formulated as an optimization problem in which model parameters such as crack location, orientation, and size are progressively updated until the model response matches the sensor data. The combination of the extended finite element method (XFEM) and genetic algorithms (GAs) has proved particularly effective for solving such inverse problem [6,7,8,9]. This effectiveness arises from the ability of XFEM to evaluate the structural response for different crack parameter values without the need for remeshing, together with the capacity of GAs to explore a complex solution space without relying on gradient information, thereby reducing the risk of being trapped in local minima.
While the GA-XFEM combination offers excellent flexibility and robustness, its computational cost remains a significant drawback. Consequently, several strategies have been investigated to accelerate the inverse problem solution, including surrogate modeling approaches based on model-order reduction techniques [10,11] and, more recently, machine learning methods [12,13,14]. Although these approaches provide advantages in specific scenarios, the former are limited by the need to update the reduced space on-the-fly, whereas the latter require large amounts of training data, which may not be available.
The extensive amount of data required to train machine learning models has prompted numerous investigations in the rapidly growing field of physics-informed machine learning [15,16], and in particular, physics-informed neural networks (PINNs) [17,18]. These approaches require substantially less data, as they rely on enforcing physical constraints. In the simplest form of the PINN approach, a neural network is employed as a global ansatz function to solve a given boundary value problem. The network parameters (weights and biases) are optimized during training by minimizing a loss function that includes the residuals of the governing partial differential equations, the boundary conditions, and any deviations from available experimental data.
While a large number of studies have applied PINNs and their variants to solid mechanics, approaches tailored to problems within the scope of linear elastic fracture mechanics remain relatively less explored [19,20,21,22,23,24,25]. One possible reason is the discontinuous nature of the solution across the crack surfaces, combined with the singular behavior near the crack tips, which necessitates the adoption of specialized strategies to mitigate convergence and accuracy issues. On the other hand, as noted by Zhang et al. [26], the meshless nature of PINNs makes them potentially ideal for solving inverse problems involving the identification of material defects based on strain or displacement measurements at discrete sensor locations. Furthermore, transfer learning (TL) can significantly enhance the efficiency of PINNs when solving sequences of problems that differ only slightly in domain geometry, as demonstrated by Chen et al. [24] for crack propagation simulations.
In addition to these developments, the emergence of holomorphic neural networks (HNNs) has significantly accelerated training for problems whose solutions can be represented by holomorphic functions [27]. A notable example is plane linear elasticity, where the Kolosov-Muskhelishvili (KM) representation [28] allows expressing the solution in terms of two complex-valued, holomorphic potentials. Accordingly, HNNs have been shown to accelerate the solution of plane elasticity problems by one to two orders of magnitude compared to standard, real-valued PINNs [27]. This improvement arises because the holomorphic formulation focuses solely on learning
This content is AI-processed based on open access ArXiv data.