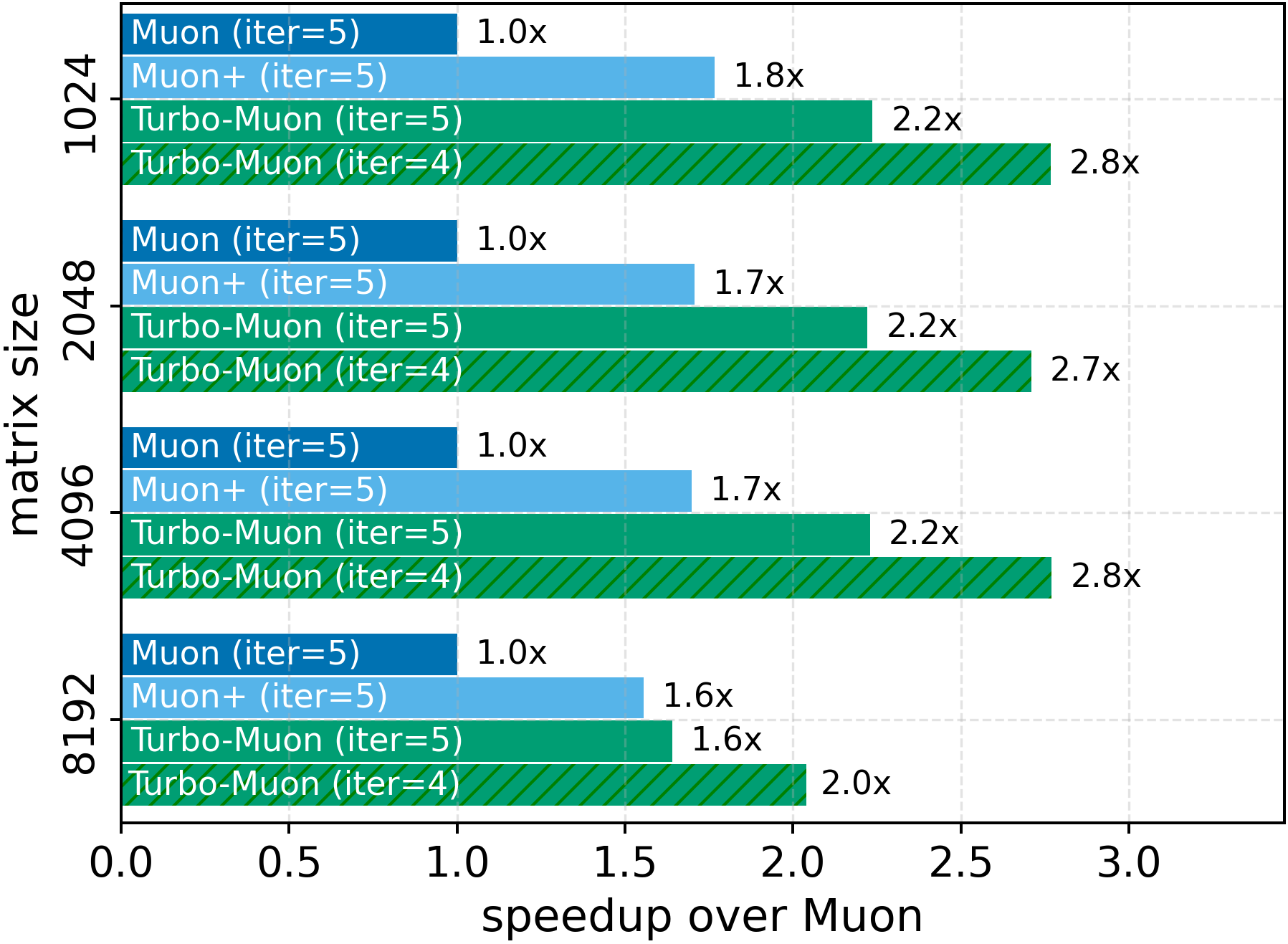
Orthogonality-based optimizers, such as Muon, have recently shown strong performance across large-scale training and community-driven efficiency challenges. However, these methods rely on a costly gradient orthogonalization step. Even efficient iterative approximations such as Newton-Schulz remain expensive, typically requiring dozens of matrix multiplications to converge. We introduce a preconditioning procedure that accelerates Newton-Schulz convergence and reduces its computational cost. We evaluate its impact and show that the overhead of our preconditioning can be made negligible. Furthermore, the faster convergence it enables allows us to remove one iteration out of the usual five without degrading approximation quality. Our publicly available implementation achieves up to a 2.8x speedup in the Newton-Schulz approximation. We also show that this has a direct impact on end-to-end training runtime with 5-10% improvement in realistic training scenarios across two efficiency-focused tasks. On challenging language or vision tasks, we validate that our method maintains equal or superior model performance while improving runtime. Crucially, these improvements require no hyperparameter tuning and can be adopted as a simple drop-in replacement. Our code is publicly available on github.
Orthogonalization of weight updates has recently become a central ingredient in several optimizers [5,6]. The most prominent example is the Muon optimizer [16], which has been shown to consistently surpass AdamW [18,25] across diverse training regimes [38] and has been adopted in large foundation models such as Kimi-K2 and GLM-4.5 [17,40]. Recent large-scale evaluations further report favorable scaling of Muon for LLM training [24,31]. In Muon and its † Core contributors. variants, updates are projected toward the orthogonal manifold to enable faster convergence, stabilize optimization, and enable robust hyperparameter transfer across model scales [4,6,22,27].
However, the computational cost of this projection remains the primary barrier to broad adoption at scale. Exact orthogonalization via SVD, while numerically precise, is impractical on modern accelerators due to its high cost and instability for large matrices in low precision. In practice, state of the art methods therefore rely on efficient but imprecise iterative schemes like the Newton-Schulz (NS) (also known as Björck) method [7,10].
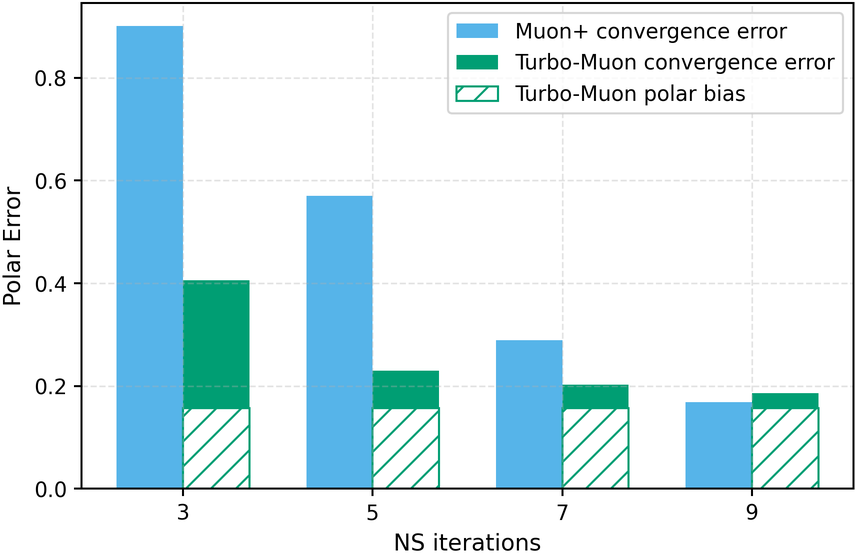
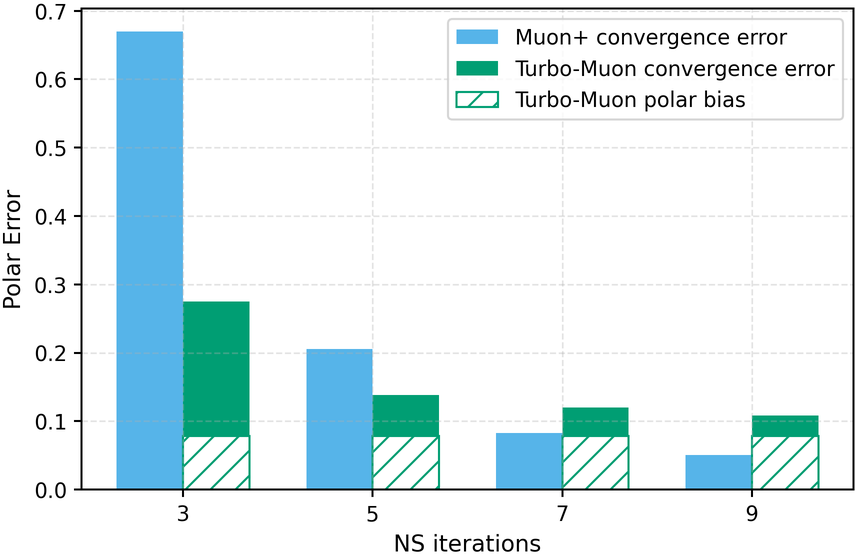
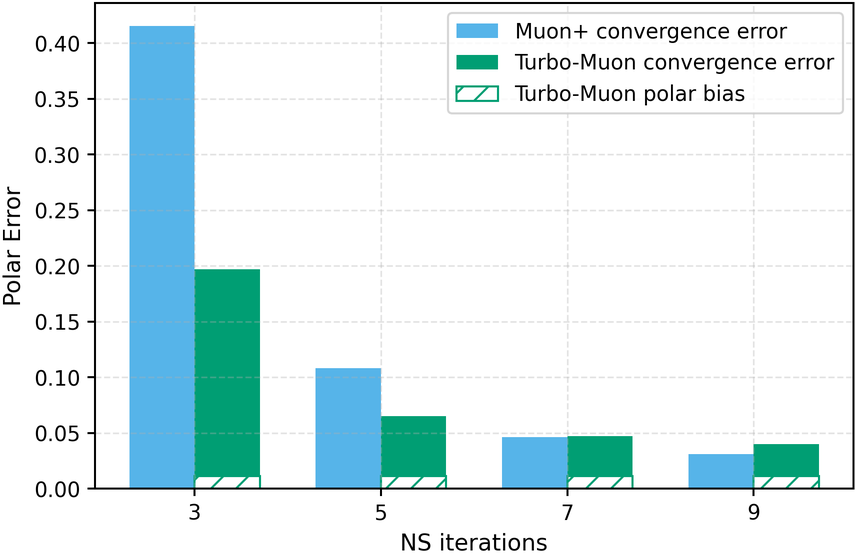
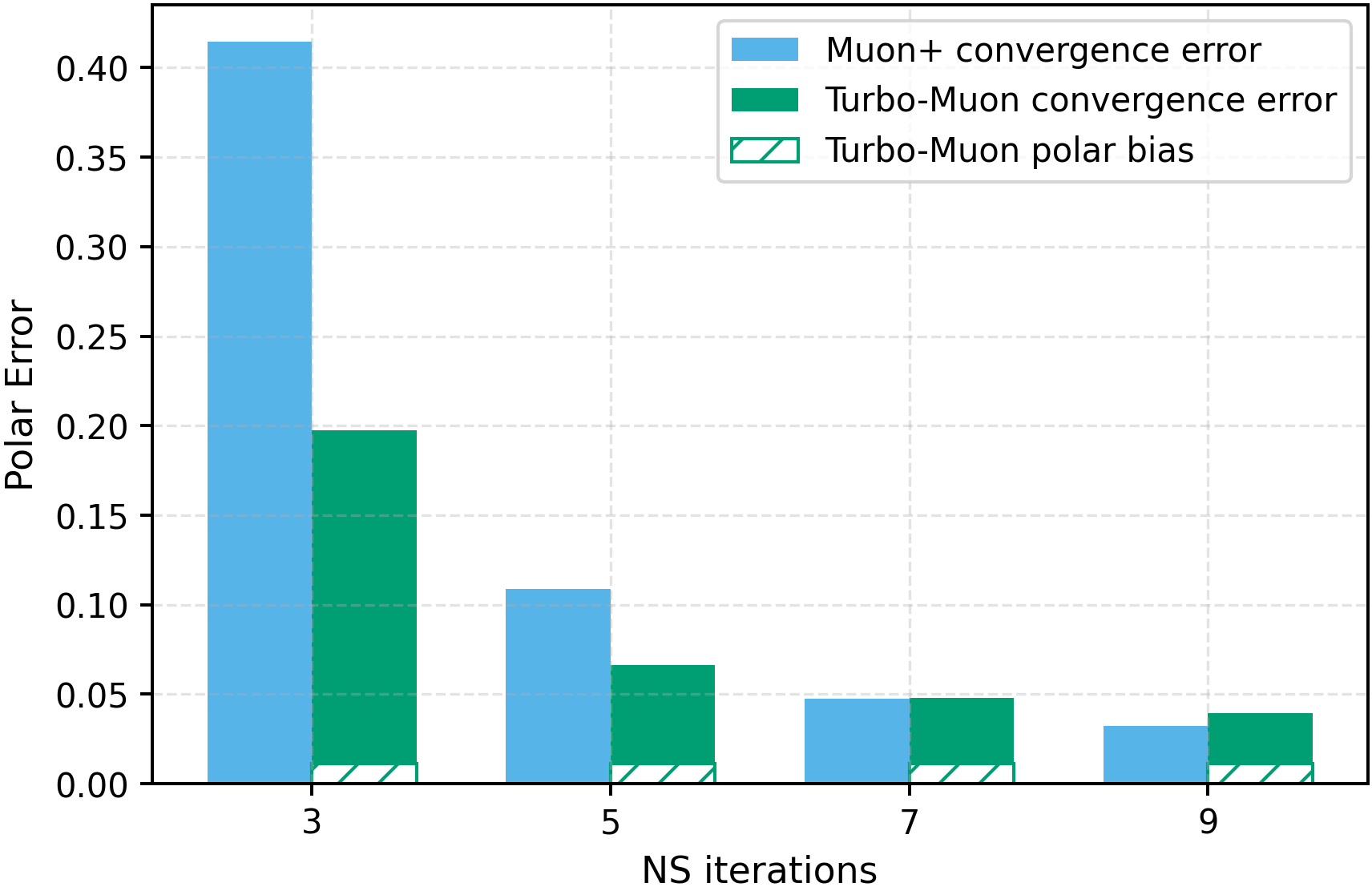
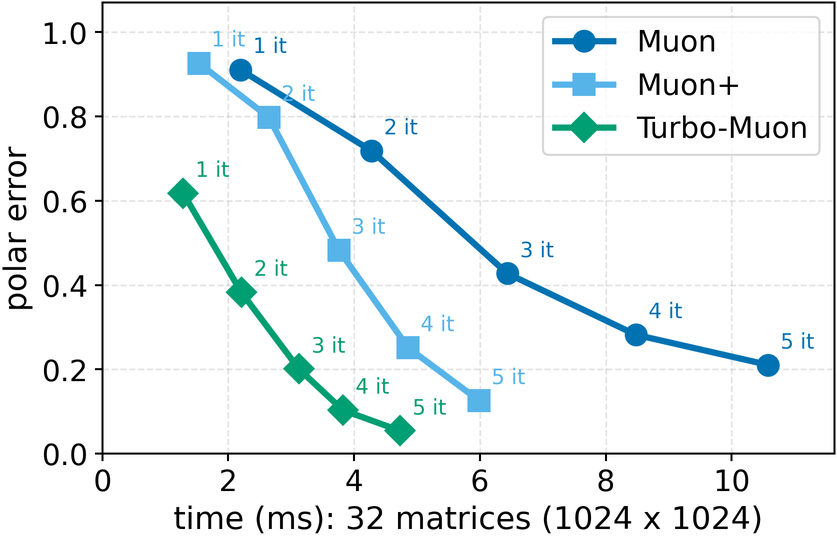
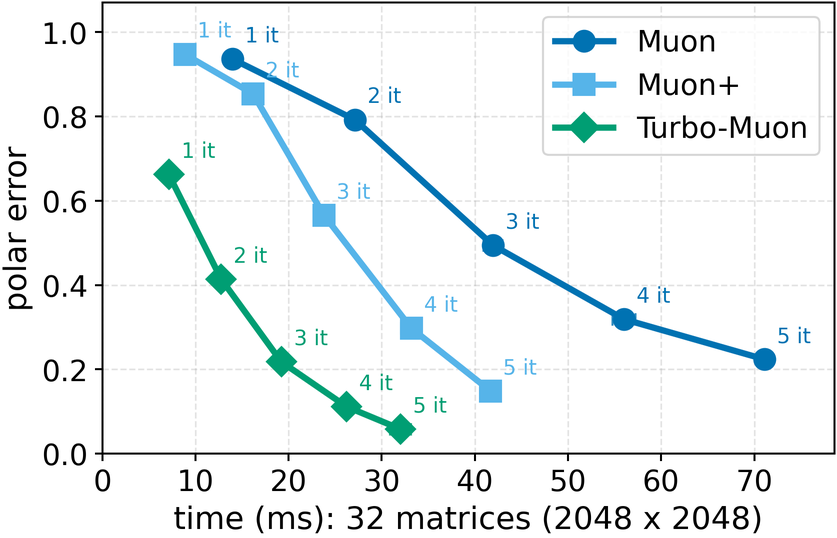
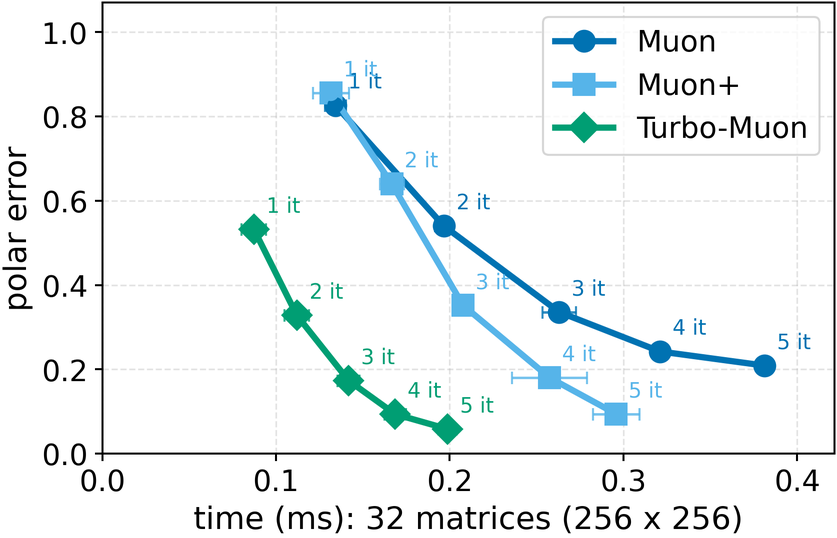
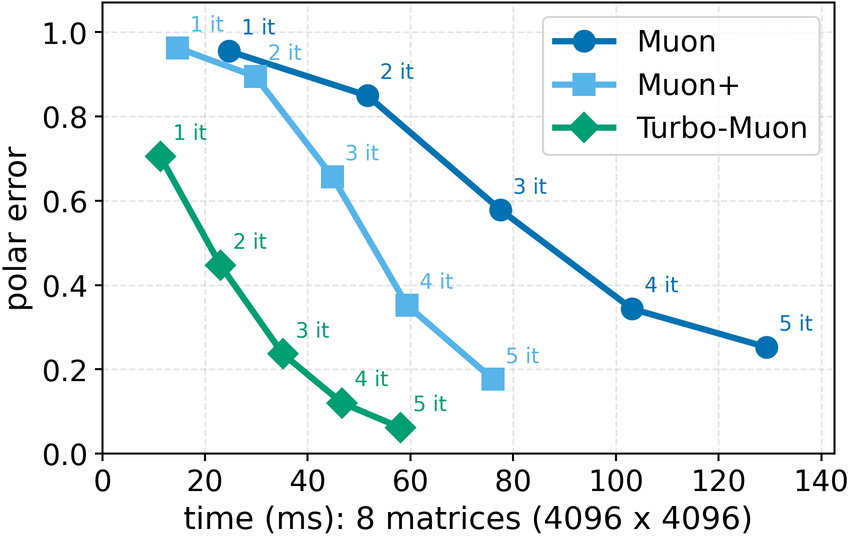
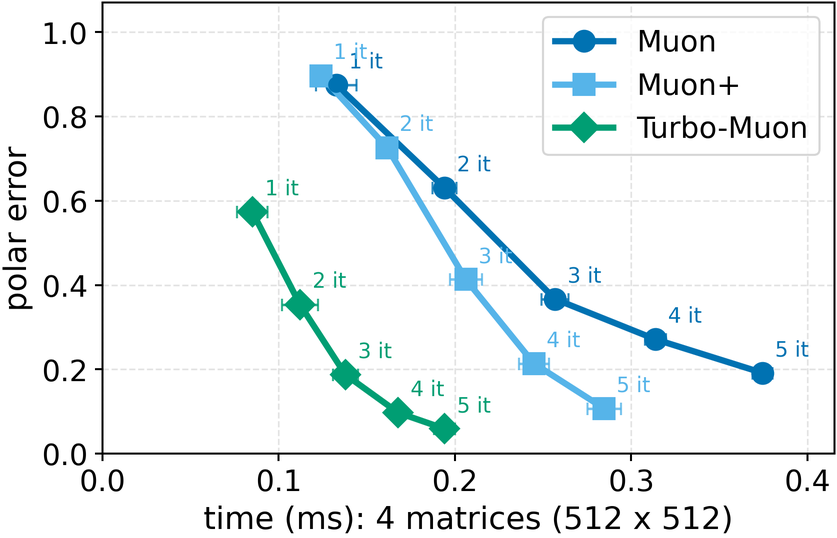
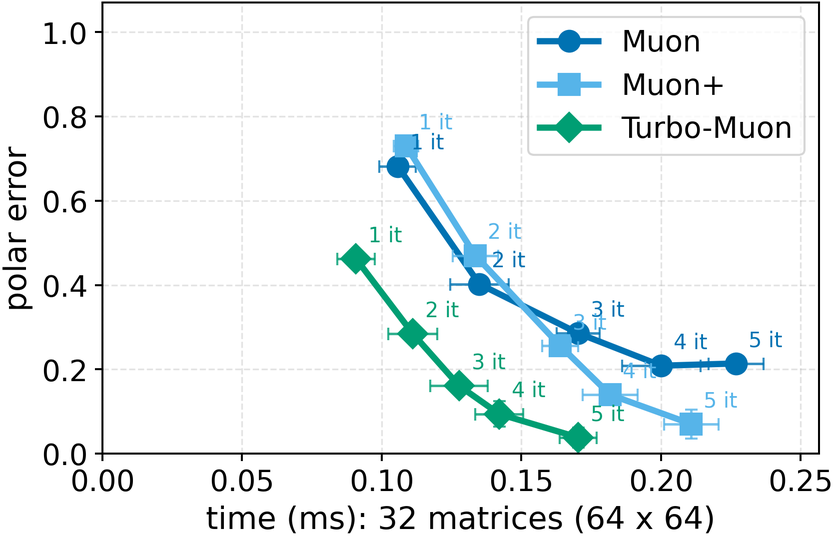
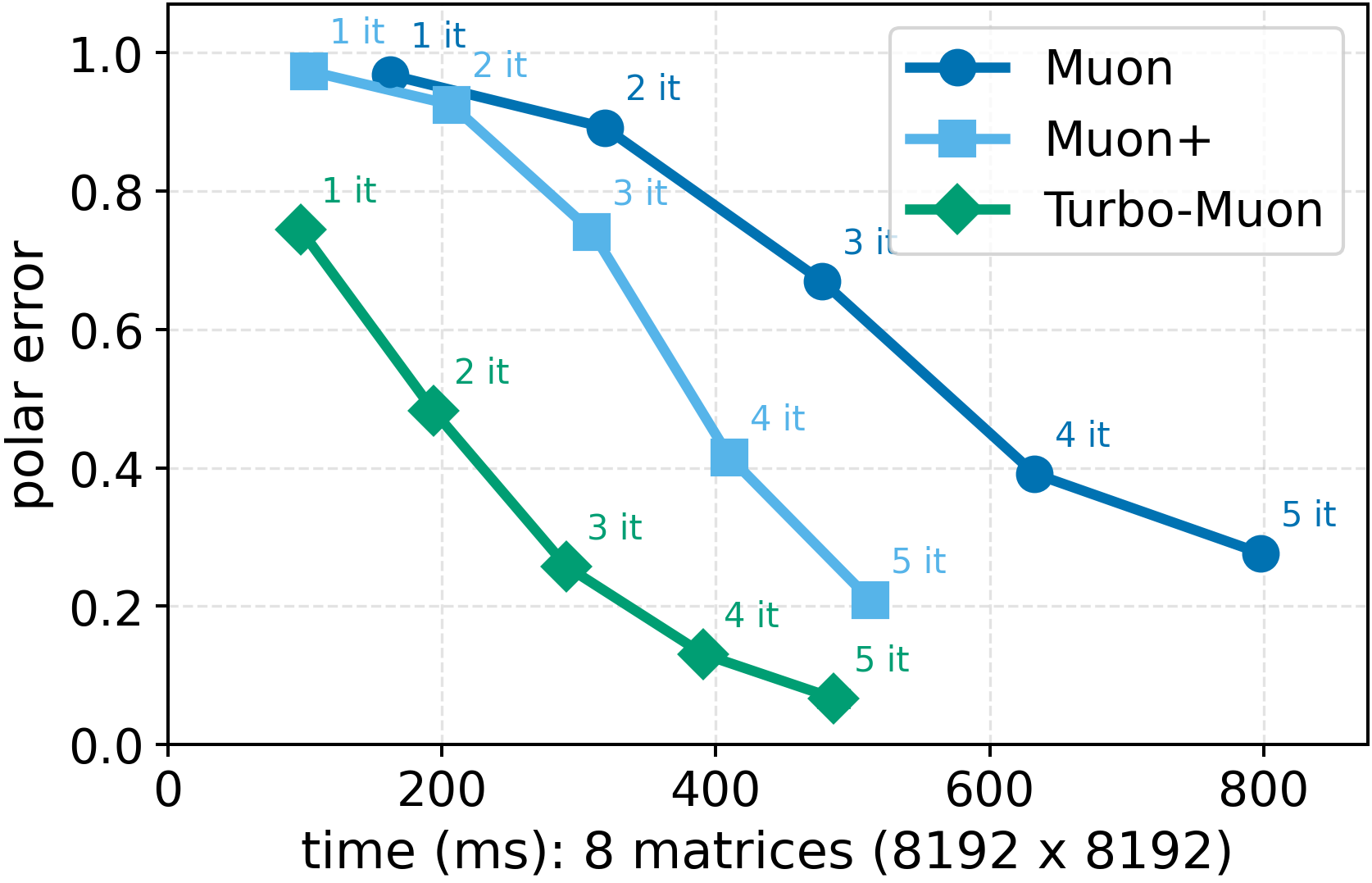
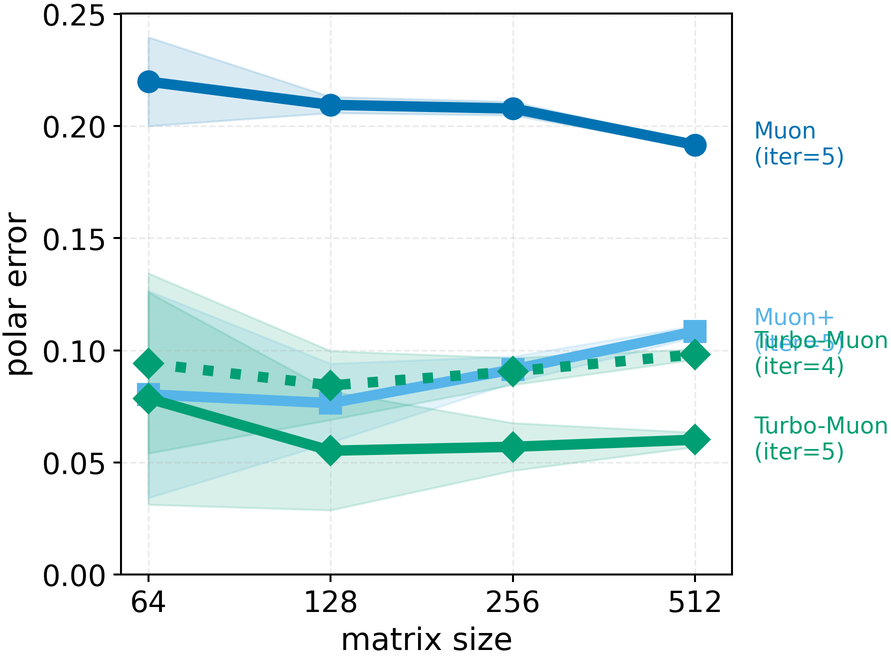
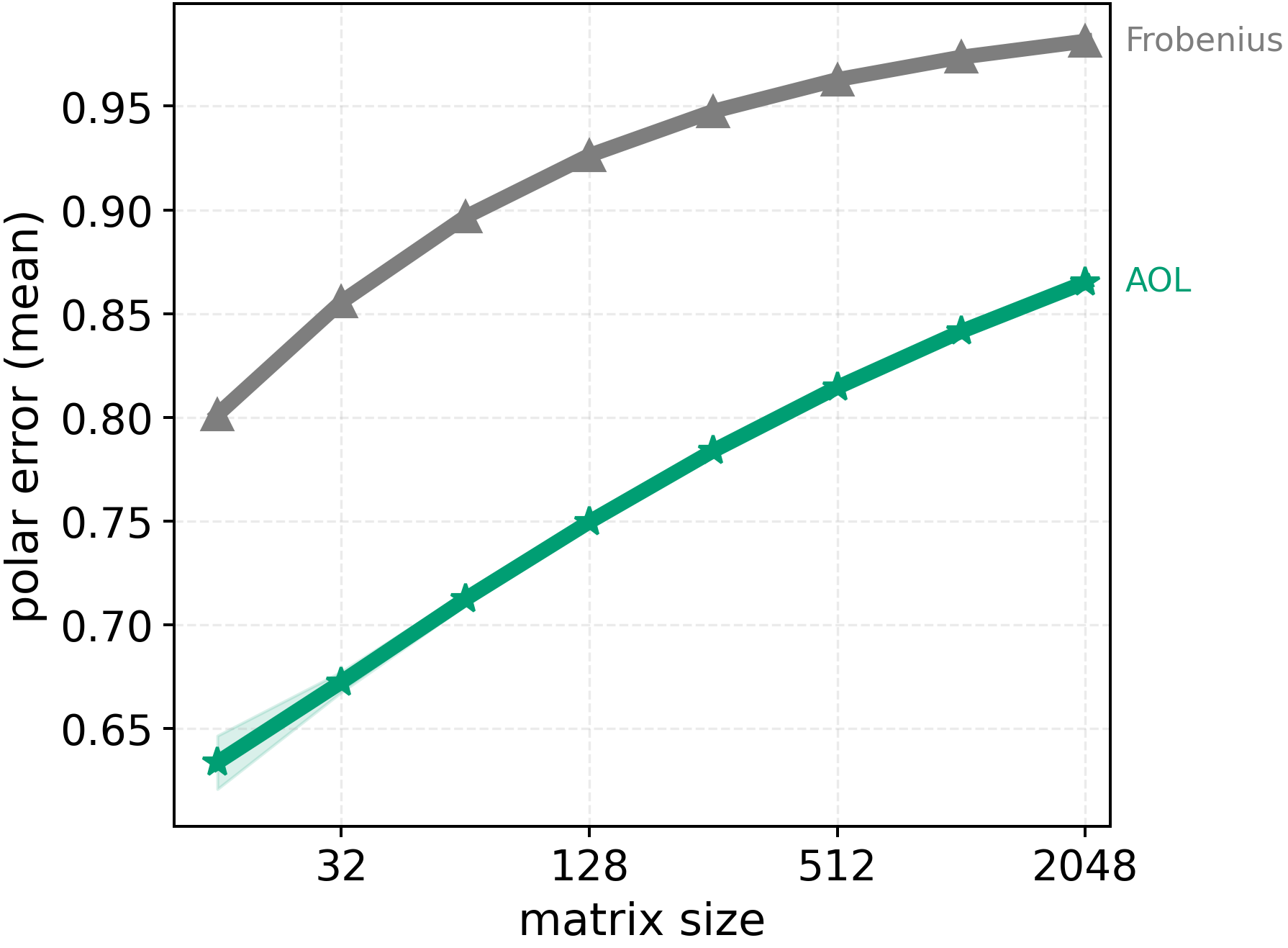
In these methods, wall-clock overhead scales with the number of iterative steps needed to achieve a target polar error (i.e., the Frobenius distance to the closest orthogonal matrix), creating a direct tension between runtime and optimization quality [32]. This paper. We introduce a preconditioned Newton-Schulz formulation based on almost-orthogonal (AOL) preconditioning [28]. Our key observation is that this preconditioner yields a substantially better initial approximation to the polar factor, especially for large matrices. In practice, this precision gain allows us to remove one Newton-Schulz iteration while improving or maintaining the numerical accuracy of the original algorithm, which typically runs in five iterations. Beyond this, the main computation cost of the preconditioner lies in an operation that can be reused, making its cost negligible. This results in an approach that yields an improved tradeoff between computation time and orthogonalization quality, as seen in Figure 1.
Finally, we test our method on a computer vision (CIFAR-10) and a language model training (nano-GPT) task and find consistent speed and convergence gains over already highly efficient baselines. Importantly, we improve training time by using a drop-in replacement for the orthogonalization step in Muon [16], our method improves runtime while preserving or improving downstream optimization performance.
Orthogonality based optimizers form a recent class of training algorithms that enforce or approximate orthogonal updates to improve conditioning and stability during deep network optimization. The foundational work of Muon [16] introduced the idea of orthogonalizing parameter updates via iterative matrix normalization, such as the Newton-Schulz method, yielding isotropic update directions and smoother convergence dynamics. Follow-ups like Deriving Muon [4] and Old Optimizer, New Norm [5] offered theoretical insights linking these methods to optimization under alternative geometries and norms. Scalable implementations such as Dion [1] extended the approach to distributed settings, while Gluon [30] and AdaMuon [33] incorporated adaptivity and layer-wise refinements, bridging the gap between theoretical LMO frameworks and practical large-model training. Empirical studies [15,17,38] further demonstrated that such orthogonalization can accelerate convergence, stabilize training under heavy-tailed gradients, and enhance performance across architectures from GPT-2 Nano to billion-parameter models. Together, these works position orthogonality-based optimization as a promising direction for efficient and stable large-scale learning.
Orthogonalization Methods. A variety of orthogonalization schemes have been proposed to construct weight matrices with orthogonal constraints. The Modified Gram-Schmidt QR factorization [21] finds the polar factor with an iterative process (one iteration per row). The Cayley transform [8] establishes a bijection between skew-symmetric and orthogonal matrices through (I -A)(I + A) -1 , though it incurs the cost of matrix inversion. The Exponential map [35] also leverages skew-symmetric matrices, generating Q = exp(A) while typically approximating the exponential via truncated series. Alternatively, the Cholesky-based method [13] orthogonalizes a matrix with a triangular decomposition M M ⊤ = LL ⊤ (where L is triangular) and solving for L -1 M , offering efficiency when numerical stability is maintained. Finally, the iterative Newton-Schulz algorithm [3,7] (also known as Björck-Bowie algorithm) projects matrices toward the Stiefel manifold via the computation of matrix polynomials, achieving fast convergence under spectral normalization. More recently, authors of [10,16] extended this algorithm with order five polynomials, achieving faster convergence. While these methods provide complementary trade-offs between ac
This content is AI-processed based on open access ArXiv data.