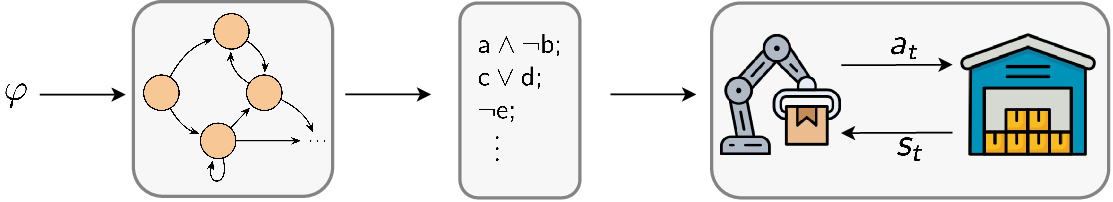Linear temporal logic (LTL) is a compelling framework for specifying complex, structured tasks for reinforcement learning (RL) agents. Recent work has shown that interpreting LTL instructions as finite automata, which can be seen as high-level programs monitoring task progress, enables learning a single generalist policy capable of executing arbitrary instructions at test time. However, existing approaches fall short in environments where multiple high-level events (i.e., atomic propositions) can be true at the same time and potentially interact in complicated ways. In this work, we propose a novel approach to learning a multi-task policy for following arbitrary LTL instructions that addresses this shortcoming. Our method conditions the policy on sequences of simple Boolean formulae, which directly align with transitions in the automaton, and are encoded via a graph neural network (GNN) to yield structured task representations. Experiments in a complex chess-based environment demonstrate the advantages of our approach.
In recent years, we have seen remarkable progress in training artificial intelligence (AI) agents to follow arbitrary instructions (Luketina et al., 2019;Liu et al., 2022;Paglieri et al., 2025;Klissarov et al., 2025). One of the central considerations in this line of work is which type of instruction should be provided to the agent; while many works focus on tasks expressed in natural language (Goyal et al., 2019;Hill et al., 2020;Carta et al., 2023), there recently has been increased interest in training agents to follow instructions specified in formal language (Jothimurugan et al., 2021;Vaezipoor et al., 2021;Qiu et al., 2023;Yalcinkaya et al., 2024;Jackermeier & Abate, 2025). As a type of programmatic task representation, formal specification languages offer several desirable properties, such as well-defined semantics and compositionality. This makes formal instructions especially appealing in safety-critical settings, in which we want to define precise tasks with a well-defined meaning, rather than giving ambiguous natural language commands to the agent (León et al., 2021).
One particular formal language that has proven to be a powerful and expressive tool for specifying tasks in reinforcement learning (RL) settings is linear temporal logic (LTL; Pnueli, 1977) (Hasanbeig et al., 2018;Hahn et al., 2019;Kuo et al., 2020;Vaezipoor et al., 2021;León et al., 2022;Liu et al., 2024). LTL instructions are defined over a set of atomic propositions, corresponding to high-level events that can hold true or false at each state of the environment. These atomic propositions are combined using logical and temporal operators, which allow for the specification of complex, non-Markovian behavior in a compositional manner, naturally incorporating aspects like safety constraints and long-term goals. Recent work has exploited the connection between LTL and corresponding automata structures (typically variants of Büchi automata; Büchi, 1966), which provide a programmatic way to monitor task progress, to train generalist policies capable of executing arbitrary LTL instructions at test time (Qiu et al., 2023;Jackermeier & Abate, 2025).
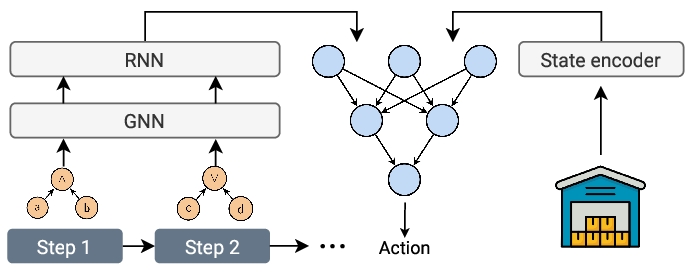
However, existing approaches often struggle in scenarios where multiple atomic propositions can hold true simultaneously. This is due to the fact that current methods treat possible assignments of propositions in isolation, and do not explicitly model the complex interactions that may occur between different high-level events. In this paper, we develop a novel approach that addresses these limitations. Our approach translates transitions in the automaton into equivalent Boolean formulae, which provide succinct, structured representations of the propositions that are relevant for making progress towards the given task, and explicitly capture the logical conditions for the transition. We show that encoding these formulae via a graph neural network (GNN) yields meaningful representations that can be used to train a policy conditioned on different ways of achieving a given task, enabling zero-shot generalization to novel LTL instructions at test time. Our main contributions are as follows:
• we develop a novel approach to learning policies for following arbitrary LTL instructions that can effectively handle complex interactions between atomic propositions;
• we propose representing LTL instructions as sequences of Boolean formulae, and show how existing policy learning approaches can be augmented with GNNs to improve representation learning;
• we introduce a novel, chess-like environment where many different propositions can be true simultaneously, which allows us to study the performance of existing approaches in this challenging setting;
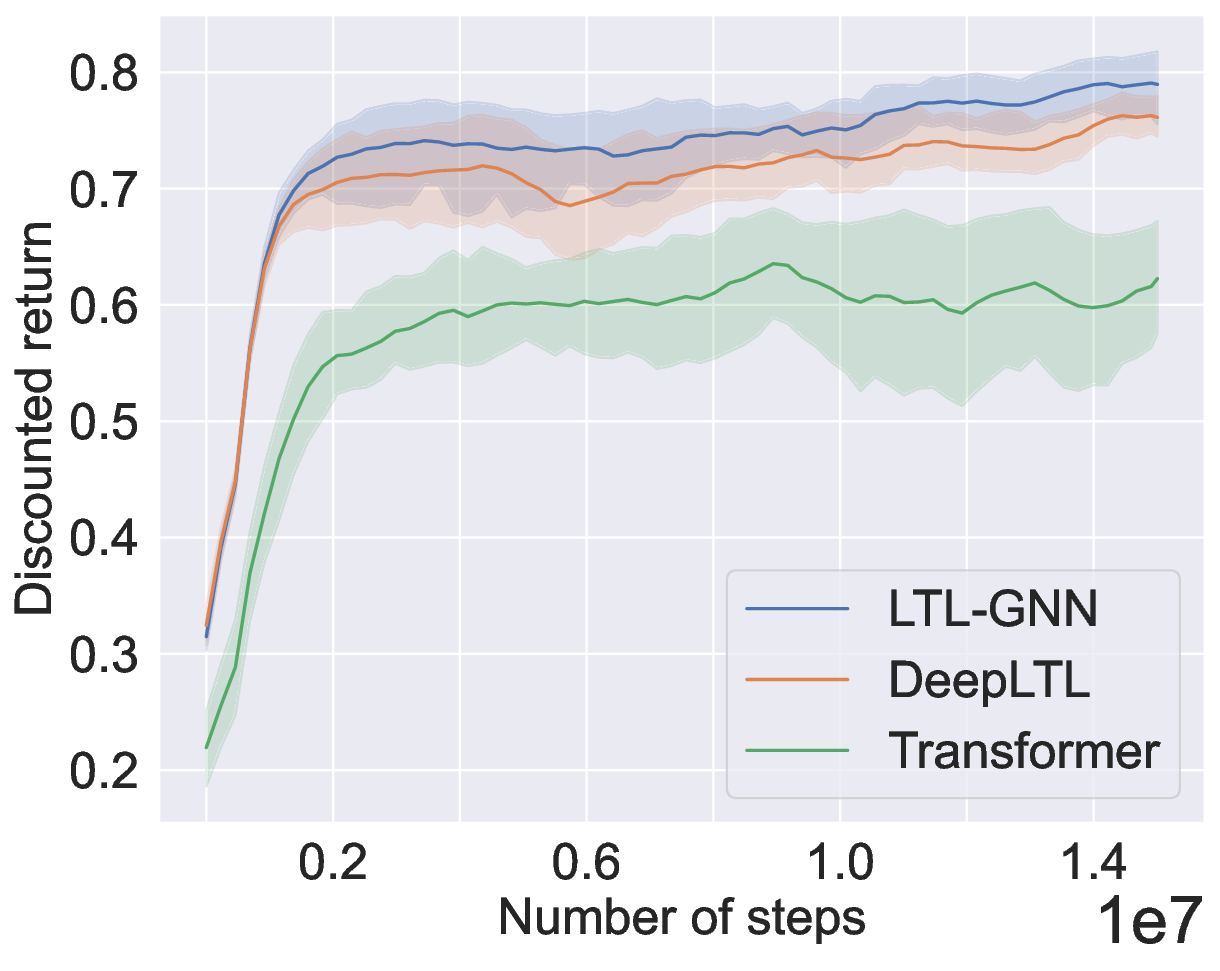
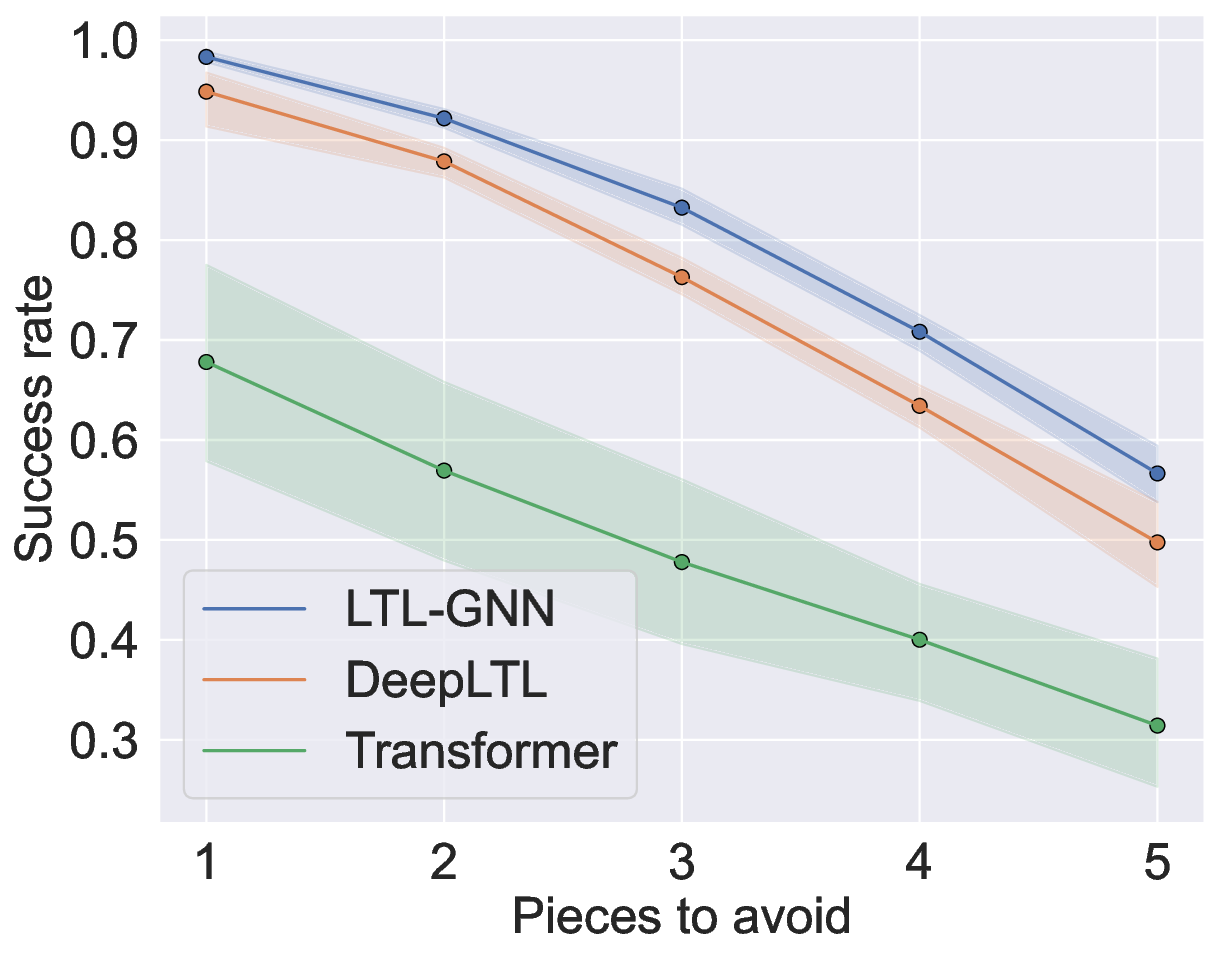
• lastly, we conduct an extensive empirical evaluation of our proposed method on this challenging environment, and show that it achieves state-of-the art results and outperforms existing methods.
While significant research effort has explored the use of LTL to specify tasks in RL (Fu & Topcu, 2014;De Giacomo et al., 2018;Hasanbeig et al., 2018;Camacho et al., 2019;Hahn et al., 2019;Bozkurt et al., 2020;Cai et al., 2021;Shao & Kwiatkowska, 2023;Voloshin et al., 2023;Le et al., 2024;Shah et al., 2025), most approaches are limited to training agents to satisfy a single specification that is fixed throughout training and evaluation. In contrast, we aim to learn a general policy that can zero-shot execute arbitrary LTL instructions at test time.
Several works have begun to tackle this challenge of learning generalist policies. Early methods, such as that of Kuo et al. (2020), propose composing recurrent neural networks (RNNs) that mirror the structure of LTL formulae, but this approach requires learning a non-stationary policy, which is generally challenging (Vaezipoor et al., 2021). Other approaches decompose LTL tasks into subtasks, which are then completed sequentially by a goal-conditioned policy (Araki et al., 2021;León et al., 2022;Liu et al., 2024;Xu &
This content is AI-processed based on open access ArXiv data.