Regime transitions routinely break stationarity in time series, making calibrated uncertainty as important as point accuracy. We study distribution-free uncertainty for regime-switching forecasting by coupling Deep Switching State Space Models with Adaptive Conformal Inference (ACI) and its aggregated variant (AgACI). We also introduce a unified conformal wrapper that sits atop strong sequence baselines including S4, MC-Dropout GRU, sparse Gaussian processes, and a change-point local model to produce online predictive bands with finite-sample marginal guarantees under nonstationarity and model misspecification. Across synthetic and real datasets, conformalized forecasters achieve near-nominal coverage with competitive accuracy and generally improved band efficiency.
Time-series forecasting often comprises hidden regime switches, which include abrupt transitions between latent operating modes characterized by changes in level, trend, volatility, or seasonality. Such shifts induce distributional nonstationarity, making not only point prediction but especially uncertainty quantification (UQ) highly challenging. By UQ, we mean the construction of wellcalibrated predictive intervals, rather than merely accurate mean forecasts, since reliable decisions depend on risk-aware intervals rather than single-value predictions.
Why UQ under regime switching is difficult. When regimes change, predictive distributions can become severely miscalibrated: intervals may undercover or inflate excessively, even when point errors remain small. Classical UQ approaches fail to handle in a proper way regime switches. For e.g., Gaussian processes with stationary kernels or Bayesian models with smooth priors implicitly assume differentiability or stationarity. These assumptions fail at regime boundaries, where the calibration typically fails. Thus, UQ in this setting requires methods that are both adaptive and robust to nonstationarity, capable of reacting online to structural shifts.
Our approach. We combine two complementary tools: (a) Deep Switching State-Space Model (DS 3 M) that explicitly incorporates a discrete regime variable to capture mode transitions while retaining continuous latent dynamics for within-regime forecasts Xu et al. [2021]; and (b) Adaptive Conformal Inference (ACI) and its aggregated variant (AgACI), which yield distribution-free predictive intervals by correcting miscoverage online in dependent time series Zaffran et al. [2022].This coupling achieves both explicit regime modeling and online calibration. In particular, DS 3 M provides regime-aware point forecasts, while ACI/AgACI ensures valid coverage guarantees despite temporal dependence and non-i.i.d. residuals. Whereas vanilla conformal prediction relies on exchangeability and fails under regime switches, adaptive updates combined with regime-aware residuals make the wrapper effective in streaming, nonstationary settings. In summary, our contributions are as follows:
• A new agnostic calibration protocol: We introduce a protocol-agnostic calibration layer for regime-switching forecasting by combining DS 3 M with adaptive conformal methods, yielding reliable, distribution-free prediction intervals.
• A new conformal-based wrapper: We propose a consistent residual-based conformal wrapper applicable across strong baselines (S4 Gu et al. [2022a], MC-Dropout GRU, CPD Truong et al. [2020], and Sparse GP), ensuring fair comparisons.
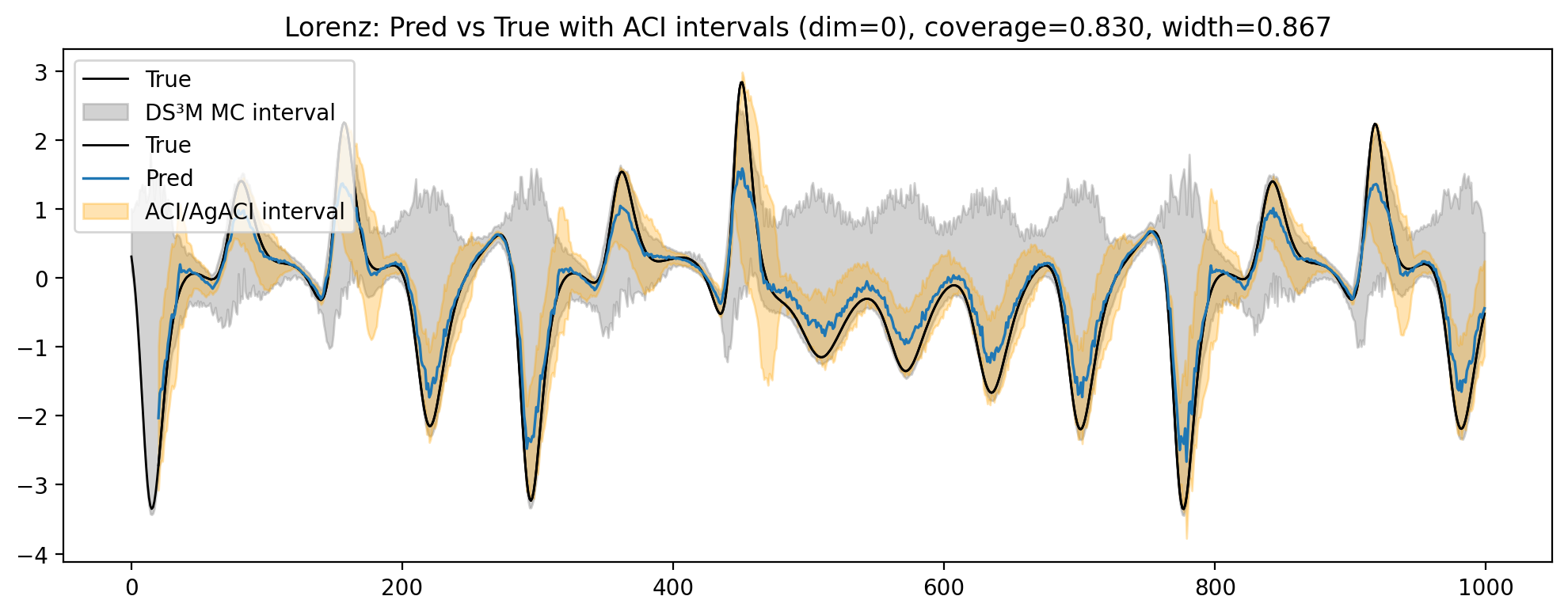
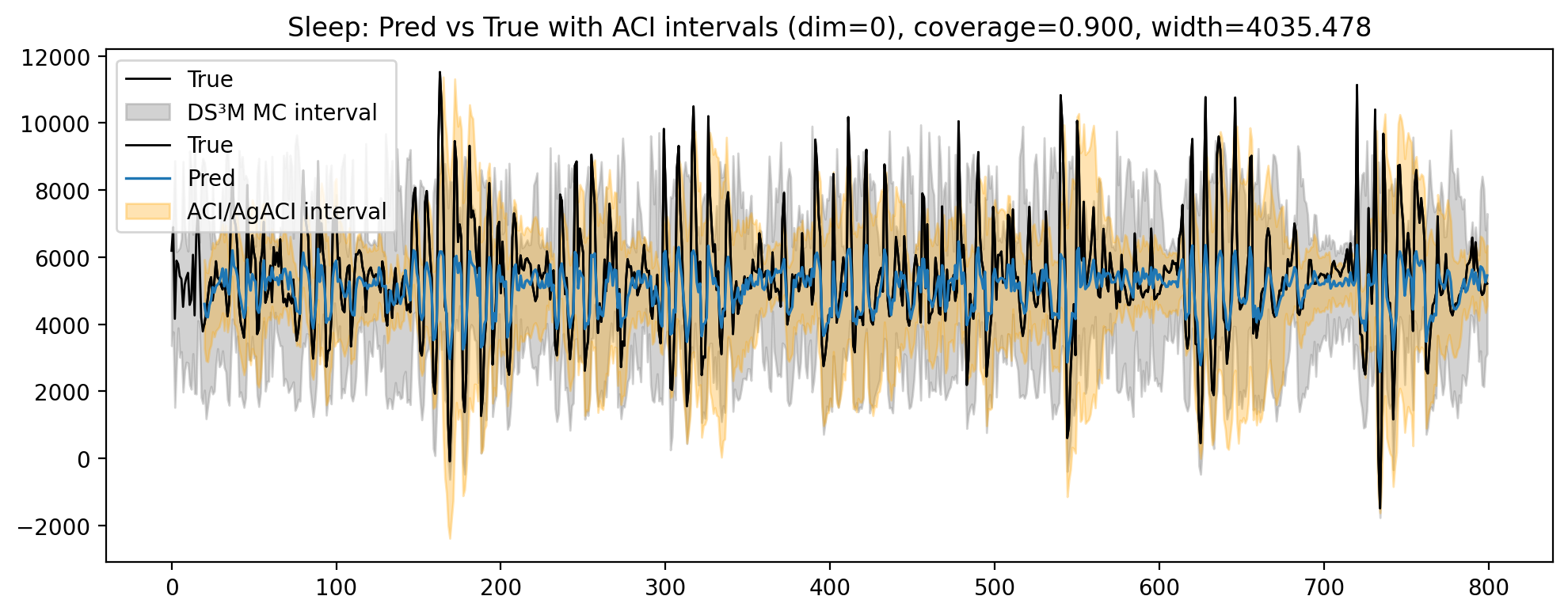
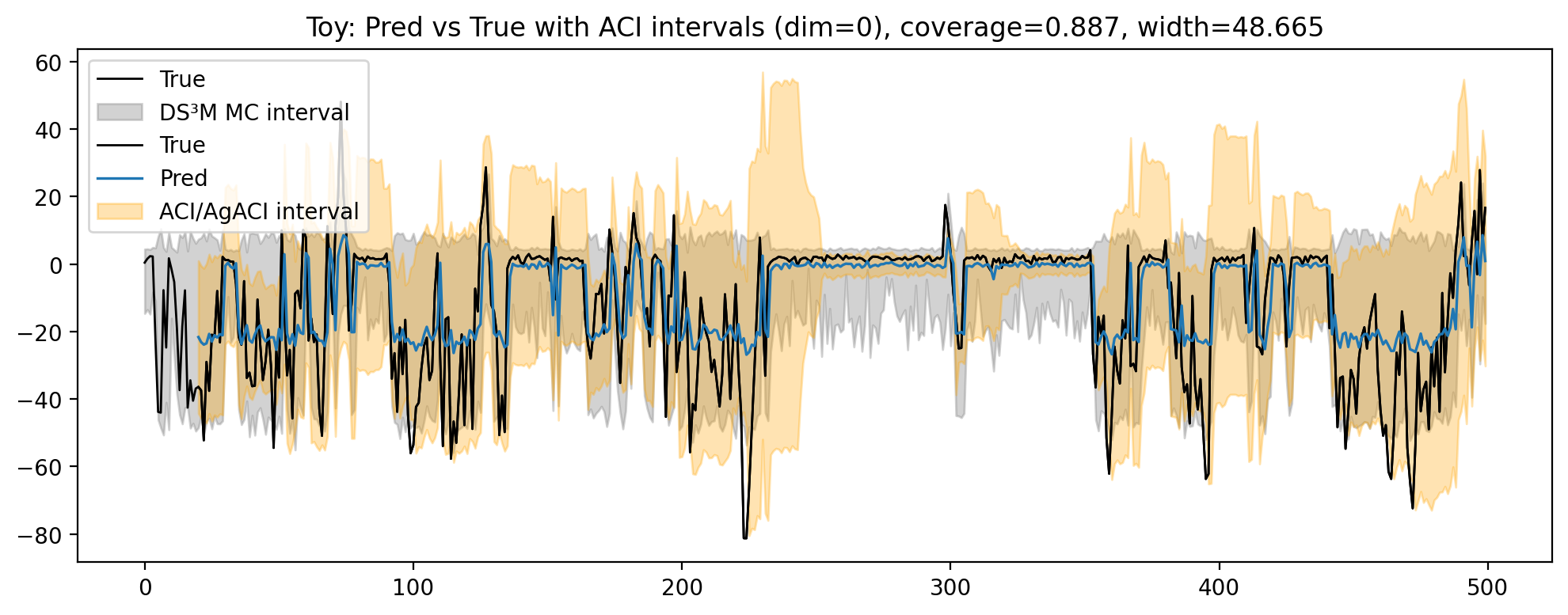
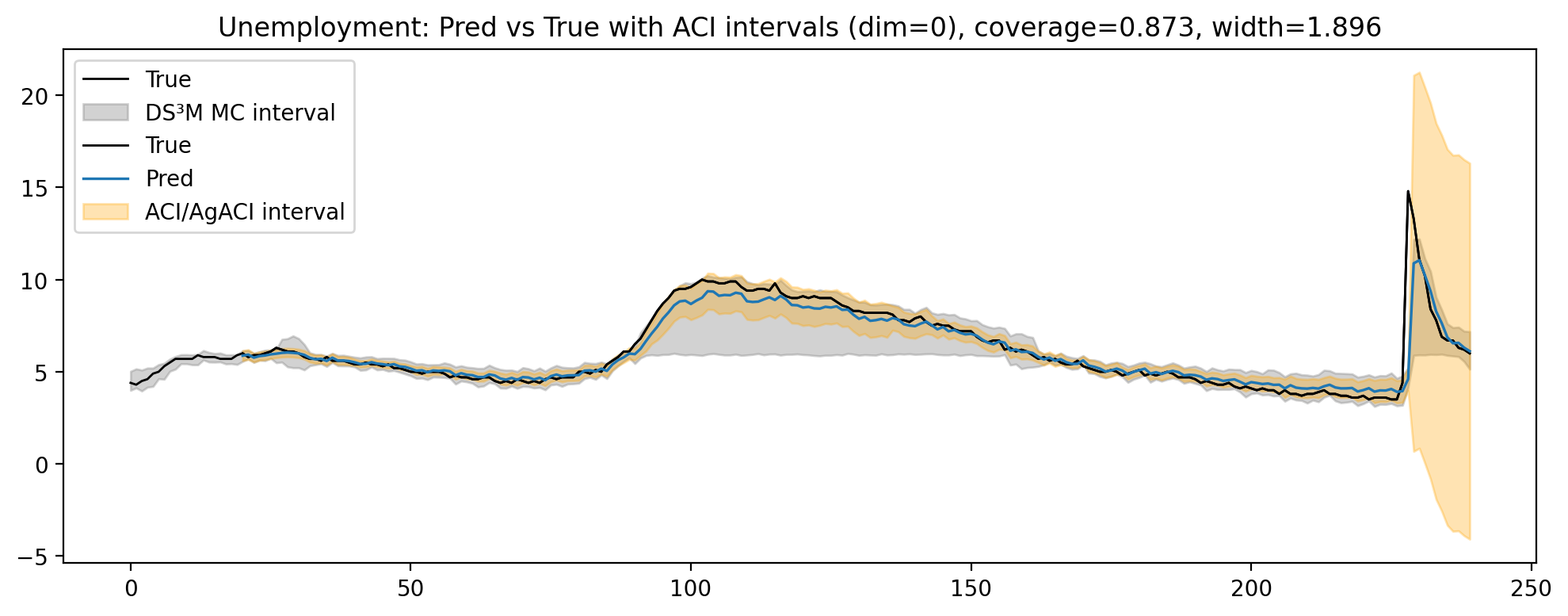
• Empirical validation in different datasets: We conduct experiments on synthetic and real datasets exhibiting regime changes, reporting coverage at 90% and median interval width. Experimental results demonstrate that our approach produces well-calibrated adaptive intervals that respond to regime shifts without sacrificing point accuracy.
Regime-switching state-space models. Classical switching state-space models (SSMs), as well as recent deep variants such as DS 3 M, incorporate a discrete regime variable to capture transitions while maintaining continuous latent states for within-regime dynamics. Variational inference enables scaling to long sequences Gu et al. [2022b]. These models offer robust regime-aware forecasting capabilities; however, their uncertainty quantification often relies on Bayesian approximations, which can be computationally expensive and prone to miscalibration following abrupt changes. Distribution-free uncertainty for time series. Conformal Prediction (CP) offers distribution-free guarantees of marginal coverage under exchangeability. However, the i.i.d. assumption breaks in time-series settings. Adaptive Conformal Inference (ACI) addresses this by correcting online for temporal dependence and distributional shifts, while Aggregated ACI (AgACI) stabilizes updates by combining multiple experts Zaffran et al. [2022]. These methods yield valid coverage in streaming data, but they do not explicitly model regime structures, limiting their responsiveness to abrupt mode changes.
Long-context state-space sequence models. Recent structured state-space layers, such as S4, efficiently capture long-range dependencies and have become strong neural backbones for sequential modeling Gu et al. [2022a]. While highly effective for point forecasting, they do not inherently address the challenges of calibrated UQ under regime switching.
Baselines for uncertainty. Several families of methods have been applied to uncertainty in nonstationary sequences. Change-point detection (CPD) explicitly segments data around structural breaks Truong et al. [2020], Bayesian deep nets such as MC-Dropout GRU Gal and Ghahramani [2016] provide scalable model-based uncertainty, and Gaussian processes (GPs) offer uncertainty quantification through kernels Li and Wang [2025]. Yet each faces limitations: G
This content is AI-processed based on open access ArXiv data.