Test-time policy optimization enables large language models (LLMs) to adapt to distribution shifts by leveraging feedback from self-generated rollouts. However, existing methods rely on fixed-budget majority voting to estimate rewards, incurring substantial computational redundancy. We propose Optimal Rollout Allocation for Test-time Policy Optimization (OptPO), a principled framework that adaptively allocates inference budgets. By formulating the voting process as a Bayesian sequential probability ratio test, OptPO dynamically halts sampling once the posterior confidence in a consensus answer exceeds a specified threshold. Crucially, it utilizes the retained rollouts for on-policy updates, seamlessly integrating with algorithms like PPO or GRPO without requiring ground-truth labels. Across diverse reasoning benchmarks, OptPO significantly reduces rollout overhead compared to fixed-sample baselines while preserving or improving accuracy. By unifying statistically optimal stopping with test-time learning, OptPO offers a computationally efficient paradigm for test-time adaptation. The source code will be open upon acceptance at https://open-upon-acceptance.
Large language models (LLMs) have achieved remarkable advances in natural language understanding, reasoning, and problem solving (Brown et al., 2020;Achiam et al., 2023). Yet, a persistent challenge emerges when models face distribution shifts at inference time, such as domain-specific terminology, unfamiliar reasoning styles, or linguistic variability, which can cause substantial performance degradation (Hu et al., 2025). To mitigate this, test-time adaptation that addresses these shifts dynamically has thus emerged as a critical research direction.
As a promising paradigm, test-time learning (TTL) enables models to learn to adapt during inference. Early methods primarily focused on light-weight adaptation without updating parameters, such as entropy minimization or batch normalization (Wang et al., 2020;Niu et al., 2022). More recent work extends these ideas to test-time training (TTT), with explicit parameter updates occurring at inference, which substantially enhances task-specific adaptability. For example, Akyürek et al. (2024) suggests that test-time training improves few-shot learning under distribution shift, while Hübotter et al. (2024) proposes active fine-tuning that selectively adapts LLMs using informative feedback signals.
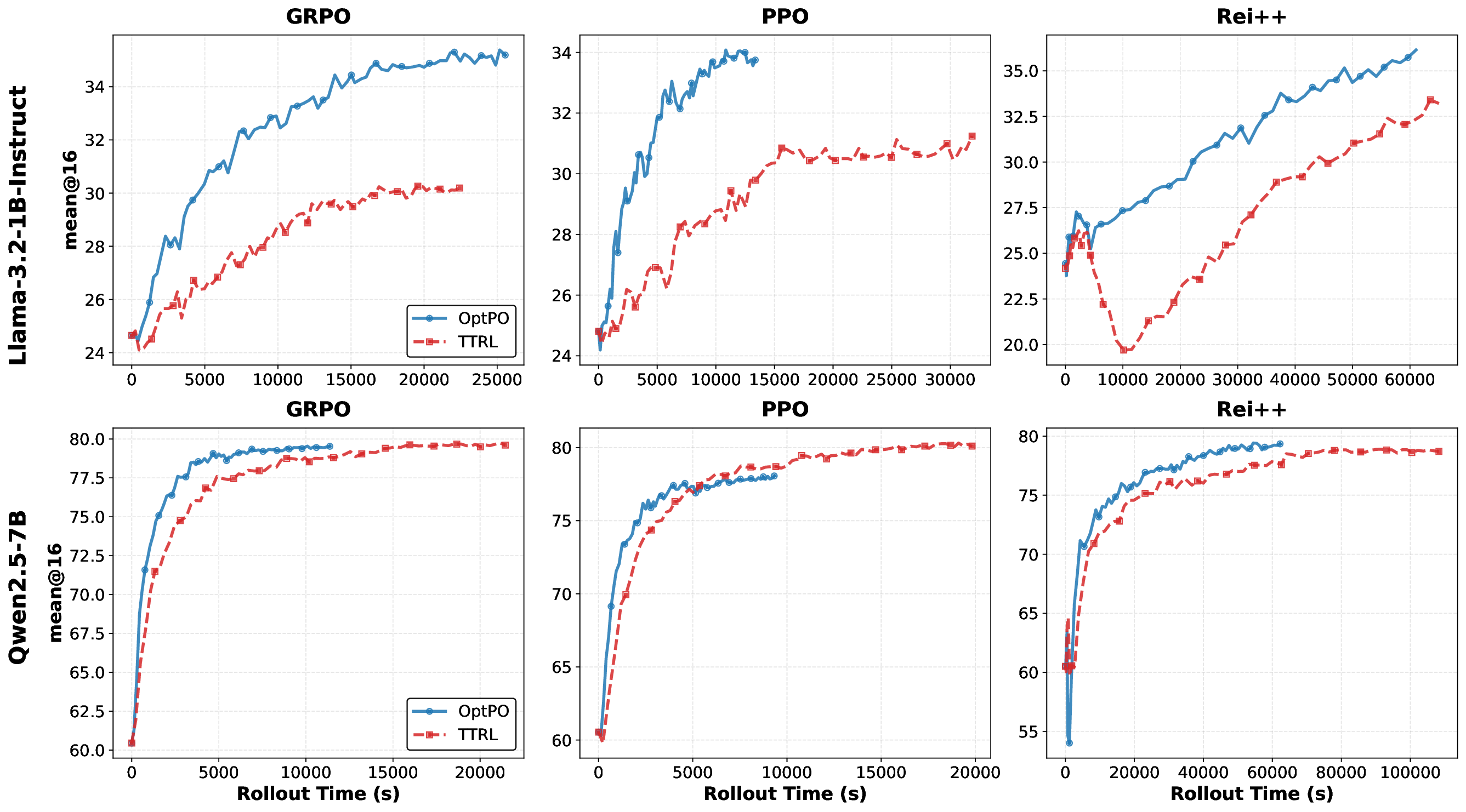
Within the TTT paradigm, a particularly emerging direction is test-time policy optimization. By treating the inference process as a reinforcement learning (RL) problem, methods such as RL with verifiable rewards (RLVR) (Wang et al., 2025) and TTRL (Zuo et al., 2025) utilize consensus-based feedback (e.g., majority voting) to guide policy updates. These approaches leverage the “wisdom of the crowd” from multiple rollouts to construct label-free rewards, effectively bridging the gap between reasoning consistency and correctness. However, a critical bottleneck remains: rollout inefficiency. Standard test-time RL methods typically mandate a fixed, large number of rollouts for every query to estimate rewards robustly. This “one-size-fits-all” strategy is computationally wasteful, as easy instances establish consensus quickly, while only hard instances require extensive sampling. Consequently, the heavy inference cost limits the practical deployment of test-time policy optimization. This paper introduces Optimal Rollout Allocation for Testtime Policy Optimization (OptPO), a general framework designed to address the efficiency-accuracy trade-off. Our key insight is to reframe reward estimation as a sequential hypothesis testing problem. Instead of pre-committing to a fixed sample budget, OptPO adaptively estimates the vote distribution using a Bayesian Sequential Probability Ratio Test (SPRT). Sampling halts as soon as the posterior evidence for a consensus answer satisfies a user-defined error tolerance. The accumulated rollouts are then immediately repurposed for policy optimization (e.g., via PPO (Schulman et al., 2017) or GRPO (Shao et al., 2024)), ensuring that compute is allocated only where necessary to reduce uncertainty. Furthermore, our OptPO can be broadly compatible with supervised fine-tuning for test-time training.
In summary, our contributions are as follows:
• We identify the fixed-budget rollout mechanism as a primary source of inefficiency in current test-time policy optimization approaches.
• We propose OptPO, a principled, plug-and-play framework for test-time policy optimization that adaptively allocates rollouts based on sequential majority voting with early stopping.
• We demonstrate that OptPO substantially reduces computational costs (e.g., over 40% savings in token consumption on the GPQA benchmark), while maintaining competitive accuracy across representative reasoning benchmarks.
By bridging ideas from test-time learning and reinforcement learning, we advance the broader goal of enabling LLMs to self-improve efficiently in dynamic environments.
Test-Time Adaptation for LLMs. Traditional machine learning assumes a fixed training-testing separation, with frozen model parameters at inference. However, models often encounter distribution shifts at test time, leading to degraded performance. Early approaches to test-time adaptation (TTA) proposed lightweight adjustments such as entropy minimization or updating normalization statistics on unlabeled test batches (Wang et al., 2020;Niu et al., 2022). These methods demonstrated effectiveness on computer vision benchmarks but remain limited in expressiveness for large language models (LLMs), where domain shift can involve complex reasoning and linguistic variability.
with D t ∈ {1, . . . , m} and cumulative vote history
Each instance is allowed a maximum rollout budget M and a minimum retained sample count N ≤ M . The goal is to form a reliable consensus pseudo-label a ⋆ using as few rollouts as possible, then update θ at test time using a small set of N retained rollouts.
Answer Probabilities. Conditioned on the true hypothesis H j , each vote equals j (the correct answer) with probability p 0 ∈ (0, 1
This content is AI-processed based on open access ArXiv data.