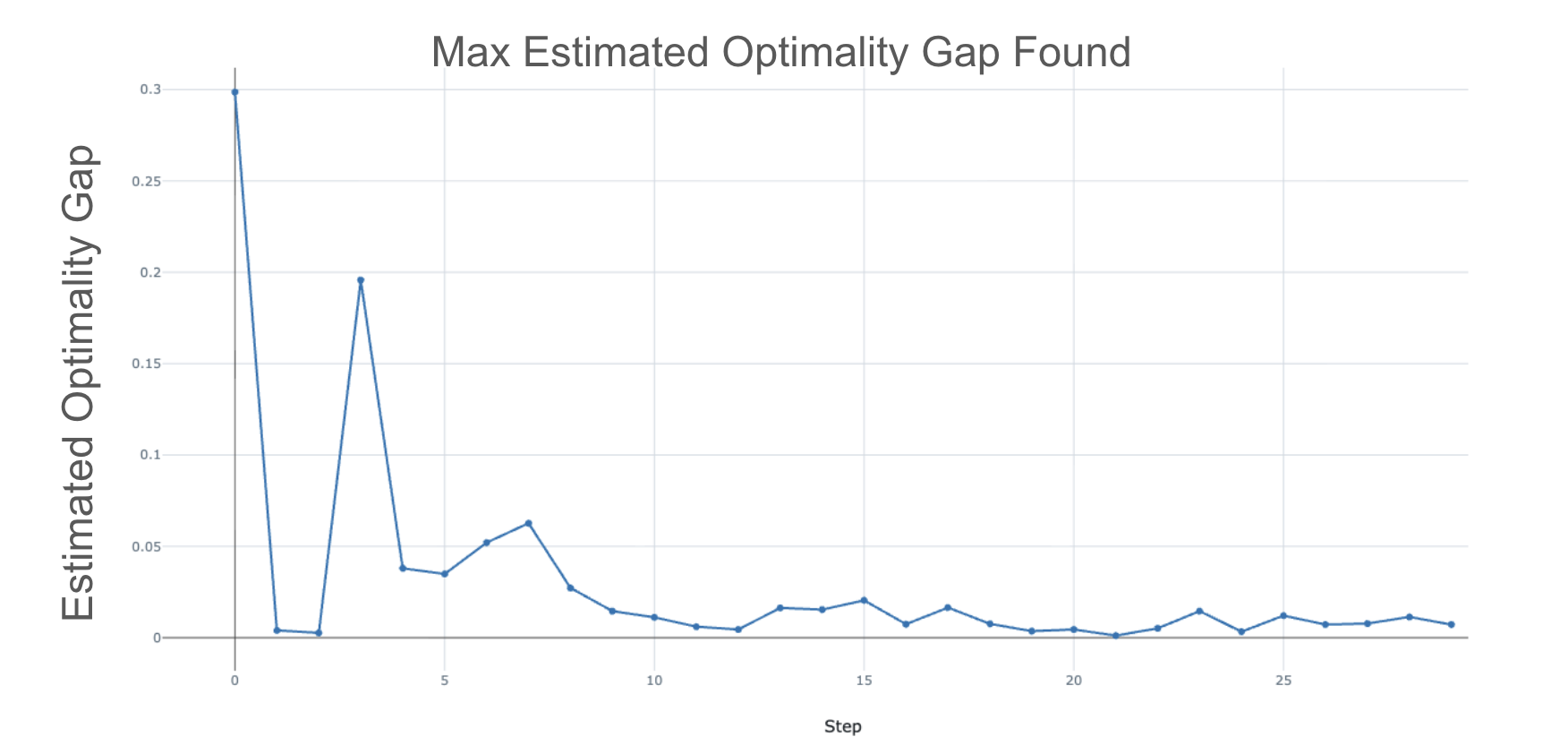
The development of tabular foundation models (TFMs) has accelerated in recent years, showing strong potential to outperform traditional ML methods for structured data. A key finding is that TFMs can be pretrained entirely on synthetic datasets, opening opportunities to design data generators that encourage desirable model properties. Prior work has mainly focused on crafting high-quality priors over generators to improve overall pretraining performance. Our insight is that parameterizing the generator distribution enables an adversarial robustness perspective: during training, we can adapt the generator to emphasize datasets that are particularly challenging for the model. We formalize this by introducing an optimality gap measure, given by the difference between TFM performance and the best achievable performance as estimated by strong baselines such as XGBoost, CatBoost, and Random Forests. Building on this idea, we propose Robust Tabular Foundation Models (RTFM), a model-agnostic adversarial training framework. Applied to the TabPFN V2 classifier, RTFM improves benchmark performance, with up to a 6% increase in mean normalized AUC over the original TabPFN and other baseline algorithms, while requiring less than 100k additional synthetic datasets. These results highlight a promising new direction for targeted adversarial training and fine-tuning of TFMs using synthetic data alone.
Recent survey studies have challenged the deep learning community to improve upon boosted tree methods for learning from structured data, having found a significant gap in performance remained between the paradigms [14]. In response, substantial progress has been made to close this gap, resulting in a variety of strong deep learning approaches being proposed over the past few years [24,13,15,16,5,27,30]. Among these new approaches, tabular foundation models (TFMs) which rely on in-context learning (ICL) [16,21,30] have emerged as a promising direction for classification and regression tasks with structured datasets. The benefits of this approach are two-fold. In many cases, the performance of the TFMs improves upon strong traditional baselines such as boosted trees [12,10]. Additionally, this performance is achieved in a zero-shot framework, enabling high-quality predictions on new datasets in milliseconds when GPU-accelerated. Further, as we will explore in this work, since these TFMs are pretrained using synthetic data, there is significant opportunity for improvement as the data generation process is expanded and improved.
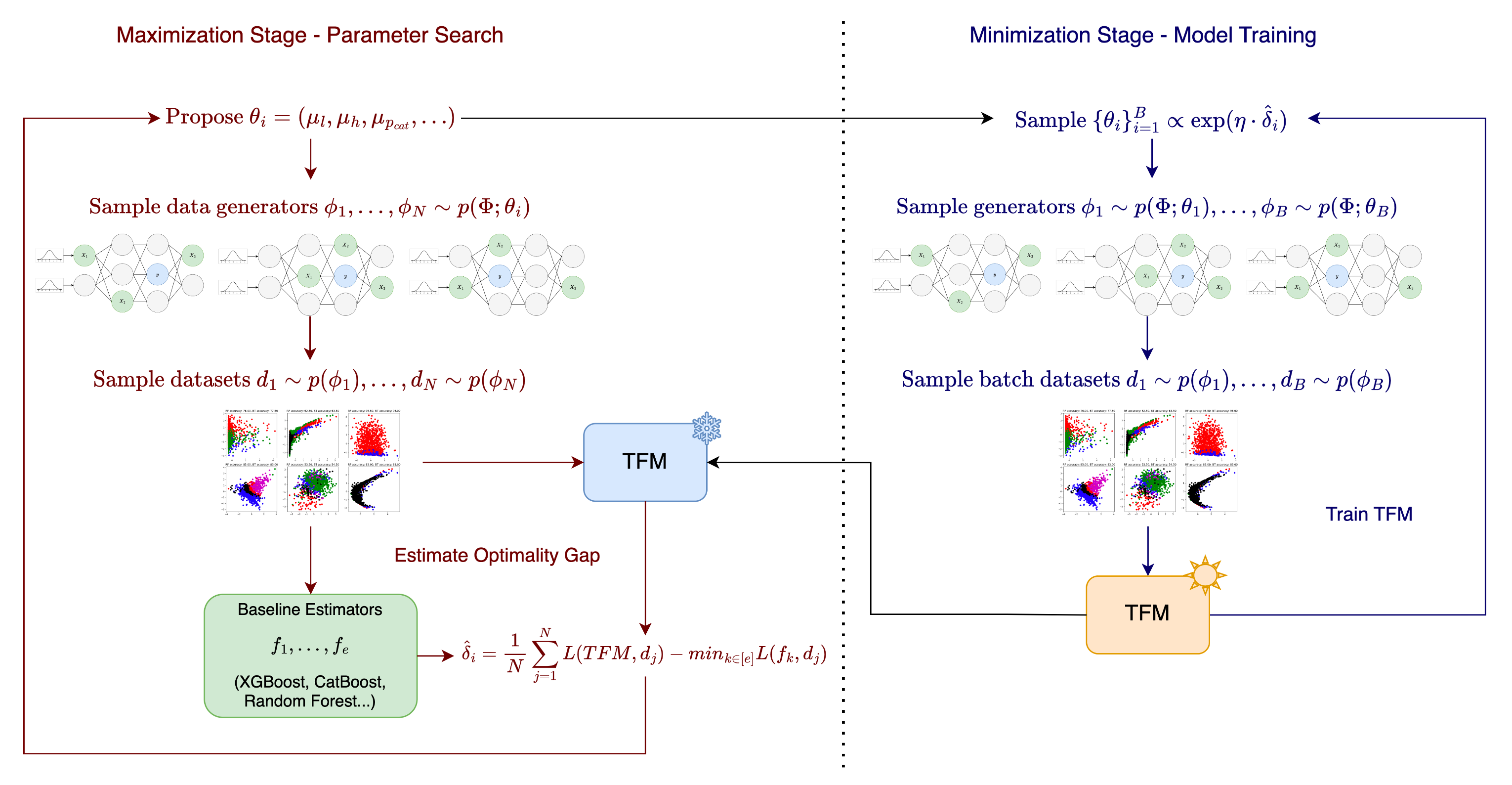
Training TFMs relies on generating a large amount of diverse synthetic datasets [16]. As we will formally define in the following section, this generation process relies on constructing structural causal models (SCMs) from which datasets can be sampled [20,23]. The structure of these SCMs is implicitly parameterized, giving significant control over the data generation process. All current publicly available, competitive TFMs [16,21,30] have been pretrained on datasets generated from a fixed prior distribution over these SCM parameters. However, fixed priors underrepresent certain regions of the parameter space, potentially degrading performance on real-world datasets with similar structure. This contributes to state-of-the-art TFMs still lagging behind tree-based methods on some benchmarks [19,29]. In this work, we leverage the significant control provided by the data generation process to frame TFM training from an adversarial robustness perspective [18]. Recent work by [26] also explores a narrower version of this idea, focusing on adjusting the weights of a specific class of SCMs in GANstyle training of TFMs. In this work, we focus on a broad and highly flexible framework for adversarially robust training of TFMs. Our contributions can be summarized as: 1) We formalize adversarial training over the SCM parameter space, allowing the model to adapt to challenging regions (e.g., varying numbers of features, categorical feature ratios, nonlinearities). We introduce an optimality gap concept and use it to target regions where the TFM underperforms relative to the best achievable performance. 2) We propose an efficient, model-agnostic two-stage adversarial training algorithm for TFMs, which we call ROBUST TABU-LAR FOUNDATION MODELS (RTFM). 3) We apply RTFM to TabPFN V2 [17], showing that with only 90k additional training datasets, we can significantly improve the ranking of TabPFN on several real-world tabular benchmarks.
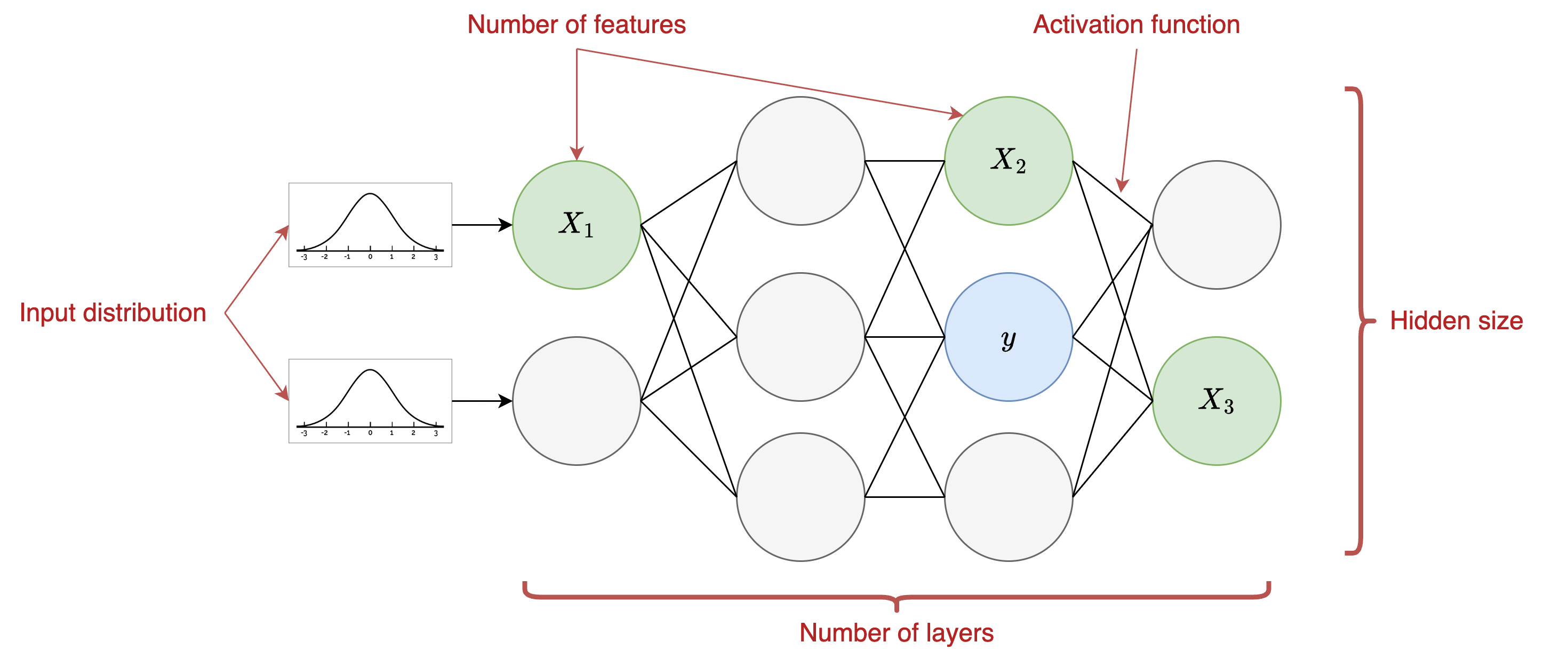
We begin by defining some notation, and then introduce our theoretical formulation for RTFM. Let Φ represent the space of hypothesis functions which define the relationship between features x and outcome y. The outcome y can be discrete or continuous, but for this work, we focus on classification tasks. Then a hypothesis ϕ ∈ Φ is a specific function which we can treat as a data generating mechanism. In the case of SCMs, Φ is the entire space of SCMs, and ϕ ∈ Φ is a specific instance of an SCM, from which a dataset D ∼ p(ϕ) can be generated. In this work, we implement SCMs as randomly initialized multi-layer perceptrons (MLPs), as introduced in [16]. Full details of this process are provided in Appendix B. For example, we can sample the number of layers l ∼ p(l), the hidden size h ∼ p(h), the activation function a ∼ p(a), and the ratio of categorical features r cat ∼ p(r cat ), among other dimensions. An SCM is generated by first sampling from the joint distribution over these hyperparameters, each of which is parameterized. For example, we might sample the ratio of categorical features r cat ∼ T runcN orm(µ rcat , a = 0, b = 1) from the truncated normal distribution with some mean µ rcat which parametrizes the distribution. Then, assuming we have similar parameterizations for the distribution over each hyperparameter, we define θ = (µ l , µ h , µ rcat , . . . ) as the parameterization of the joint distribution over all the hyperparameters. We define P as the space of the parameters, such that θ ∈ P. The generators are then sampled from ϕ ∼ p(Φ; θ).
We now define the original objective for the Prior-Fitted Network (PFN) learning task and provide our adversarially robust formulation. Let g W be our predictive model parameterized by weight matrix W. As a PFN, g W takes as input a sequence of labeled training samples and unlabeled test samples, and predicts labels for the
This content is AI-processed based on open access ArXiv data.