Graph Distance as Surprise: Free Energy Minimization in Knowledge Graph Reasoning

Graph Distance as Surprise: Free Energy Minimization in Knowledge Graph Reasoning Gaganpreet Jhajj1,*, Fuhua Lin1 1School of Computing and Information Systems, Athabasca University, Canada Abstract In this work, we propose that reasoning in knowledge graph (KG) networks can be guided by surprise minimization. Entities that are close in graph distance will have lower surprise than those farther apart. This connects the Free Energy Principle (FEP) [1] from neuroscience to KG systems, where the KG serves as the agent’s generative model. We formalize surprise using the shortest-path distance in directed graphs and provide a framework for KG-based agents. Graph distance appears in graph neural networks as message passing depth and in model-based reinforcement learning as world model trajectories. This work-in-progress study explores whether distance-based surprise can extend recent work showing that syntax minimizes surprise and free energy via tree structures [2]. Keywords Knowledge Graphs, Graph Neural Networks, Active Inference, Semantic Grounding, Agents 1. 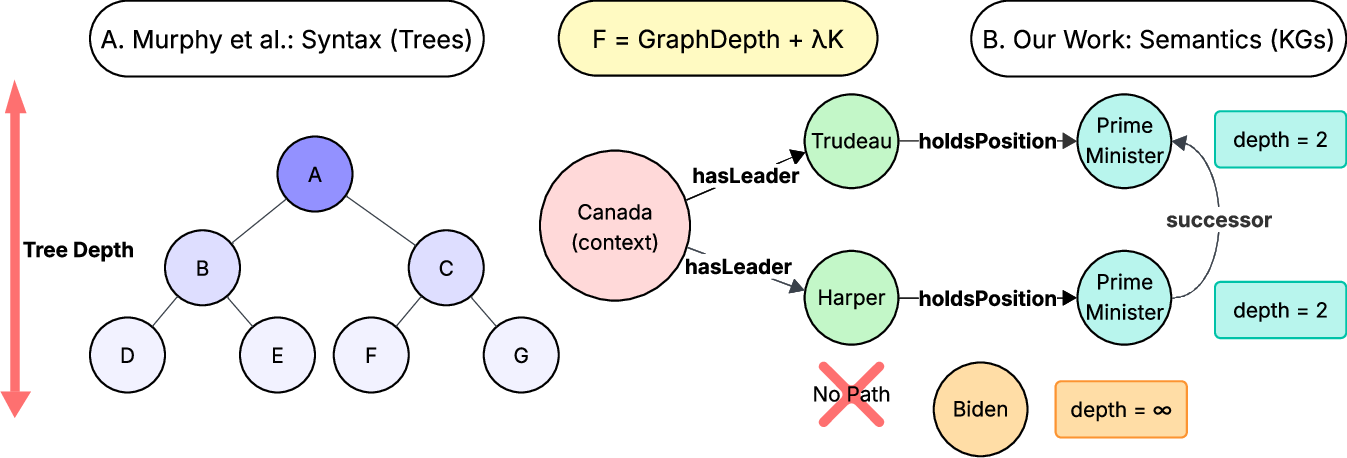Introduction The Free Energy Principle (FEP) suggests that biological systems minimize surprise by maintaining accurate world models [1, 3, 4]. Recently, Murphy et al. [2] demonstrated that syntactic operations minimize surprise through shallow tree structures. They quantified surprise via tree depth (geometric complexity) and Kolmogorov complexity (algorithmic complexity), approximated through Lempel-Ziv compression [5, 6]. In FEP, agents minimize variational free energy 𝐹= −log 𝑃(𝑜, 𝑠) −𝐻[𝑄(𝑠)], where 𝑜represents observations, 𝑠hidden states, 𝑃the generative model, and 𝑄the agent’s beliefs [1]. The first term, −log 𝑃(𝑜, 𝑠), quantifies surprise: entities with high probability under the generative model (high 𝑃(𝑜, 𝑠)) yield low surprise (low −log 𝑃(𝑜, 𝑠)). For syntactic trees, Murphy et al. [2] used tree depth to proxy this probability; we extend this principle to general graphs using shortest-path distance. In active inference, minimizing free energy drives both perception (updating beliefs 𝑄(𝑠)) and action (selecting policies that reduce uncertainty) [3]. We apply this principle to KG reasoning: entities at shorter graph distances have a higher probability under the agent’s graph-based generative model. The central question we address is: given a KG serving as an agent’s generative model, which entity groundings are plausible for a query in context? We propose one principled approach: plausibility inversely correlates with graph distance. Knowledge graphs (KGs) are increasingly integrated with modern AI agents, with the ability to improve reasoning, memory, and planning [7, 8, 9, 10, 11, 12, 13, 14, 15, 16]. Unlike syntactic tree structures, KGs are directed graphs that can contain cycles and multiple paths between nodes (entities). In this preliminary work, we propose that surprise in KG reasoning corresponds to graph distance, where the KG serves as the agent’s generative model. Entities that require shorter paths from context are unsurprising, whereas distant or disconnected entities are more surprising. This is unlike surprise- driven exploration in RL [17, 18], where agents maximize surprise to explore, FEP agents minimize surprise by maintaining accurate generative models. Our work connects the FEP to practical KG systems through shortest-path distance, providing theoretical foundations for graph neural networks [19, 20, 21] and model-based reinforcement learning [22, 23]. NORA’25: 1st Workshop on Knowledge Graphs & Agentic Systems Interplay co-located with NeurIPS, Dec.1, 2025, Mexico City, Mexico $ gjhajj1@learn.athabascau.ca (G. Jhajj); oscarl@athabascau.ca (F. Lin)  0000-0001-5817-0297 (G. Jhajj); 0000-0002-5876-093X (F. Lin) © 2025 Copyright for this paper by its authors. Use permitted under Creative Commons License Attribution 4.0 International (CC BY 4.0). 2. From Syntax to Semantics Murphy et al. [2] quantified syntactic surprise via tree depth. We extend this to arbitrary directed graphs with cycles. Given a KG 𝒢= (ℰ, ℛ, 𝒯) with entities ℰ, relations ℛ, and triples 𝒯⊆ℰ× ℛ× ℰ, geometric surprise is: 𝑆geo(𝑒| 𝐶) = ⎧ ⎨ ⎩ min 𝑐∈𝐶𝑑𝒢(𝑐, 𝑒) if path exists 𝛼 otherwise (1) where 𝑑𝒢(𝑐, 𝑒) is the shortest directed path length from context 𝑐∈𝐶to entity 𝑒(computed via BFS, Appendix B), and 𝛼is a hyperparameter penalizing disconnection. In our worked example, we set 𝛼= 5; in general, 𝛼should exceed the graph’s diameter (longest shortest-path distance) to ensure disconnected entities always have higher surprise than any connected entity. Combined with algorithmic complexity [2]: 𝐹(𝑒| 𝐶) = 𝑆geo(𝑒| 𝐶) + 𝜆𝐾(𝜋𝐶→𝑒) (2) where 𝐾(𝜋𝐶→𝑒) is Kolmogorov complexity of the relation path, approximated via Lempel-Ziv compres- sion, and 𝜆weights the components. For trees, this recovers Murphy’s tree depth; for general graphs, it handles cycles naturally. Connection to FEP: Under FEP, agents minimize 𝐹= −log 𝑃(𝑜, 𝑠) −𝐻[𝑄(𝑠)] [1]. Interpreting the KG as the agent’s genera

This content is AI-processed based on open access ArXiv data.