This paper proposes a unified software architecture for visualization and simulation based on a design targeting an $N$-dimensional space. The contribution of this work lies in presenting an architectural configuration that integrates multiple processes into a single software architecture: Quickhull-based convex hull mesh generation, Boolean operations, coordinate transformations for high-dimensional exploration (including orientation and view transformations), and hyperplane slicing for visualization. The proposed approach adopts an approximate implementation that tolerates numerical errors and prioritizes implementation transparency over guarantees of numerical rigor. The experimental results and evaluations presented in this paper are limited to a 4D implementation; no evaluation is conducted for $N>4$, and the discussion is restricted to stating that the architecture itself has a dimension-independent structure. This paper also proposes an interaction design for high-dimensional exploration based on FPS navigation. As an input example involving shape changes over time, a non-rigid body simulation based on XPBD (Extended Position Based Dynamics) is integrated into the 4D implementation. Experimental results confirm that the 4D implementation runs on a single PC.
This paper builds on prior work on visualization and simulation in high-dimensional spaces. However, examples remain limited that integrate Quickhull-based convex hull mesh generation, Boolean operations, coordinate transformations for high-dimensional exploration (orientation and view transformations), and hyperplane slicing for visualization into a single software architecture, under the assumption of an iterative workflow of user actions and result inspection. In this work, we propose a unified architecture intended for use by researchers and developers. While this architecture is designed for an N -dimensional space, the present study implements and evaluates it in 4D.
The contribution of this work is to present an architectural configuration that integrates the above processing components as a single software architecture and to evaluate the 4D implementation experimentally.
In this paper, interactivity is defined as a workflow that presupposes repeated cycles of user actions and result inspection, in contrast to offline batch processing in which input conditions are fixed in advance and executed in a single run. Hereafter, the term “interactive,” including its adjectival and adverbial usages, refers to usage scenarios that satisfy or require this notion of interactivity.
Prior work on visualization and simulation in highdimensional spaces is often reported in terms of individual elemental techniques.
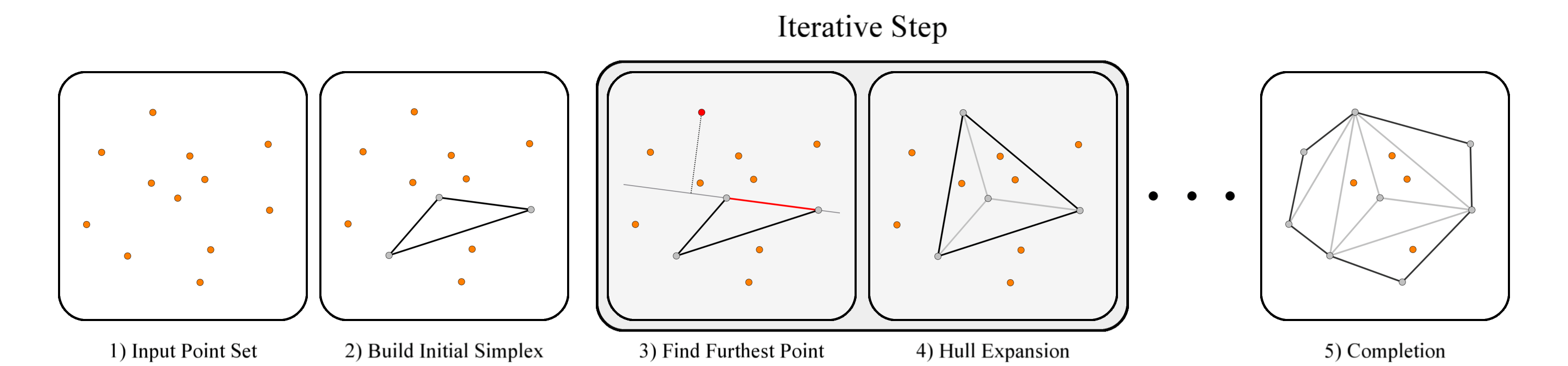
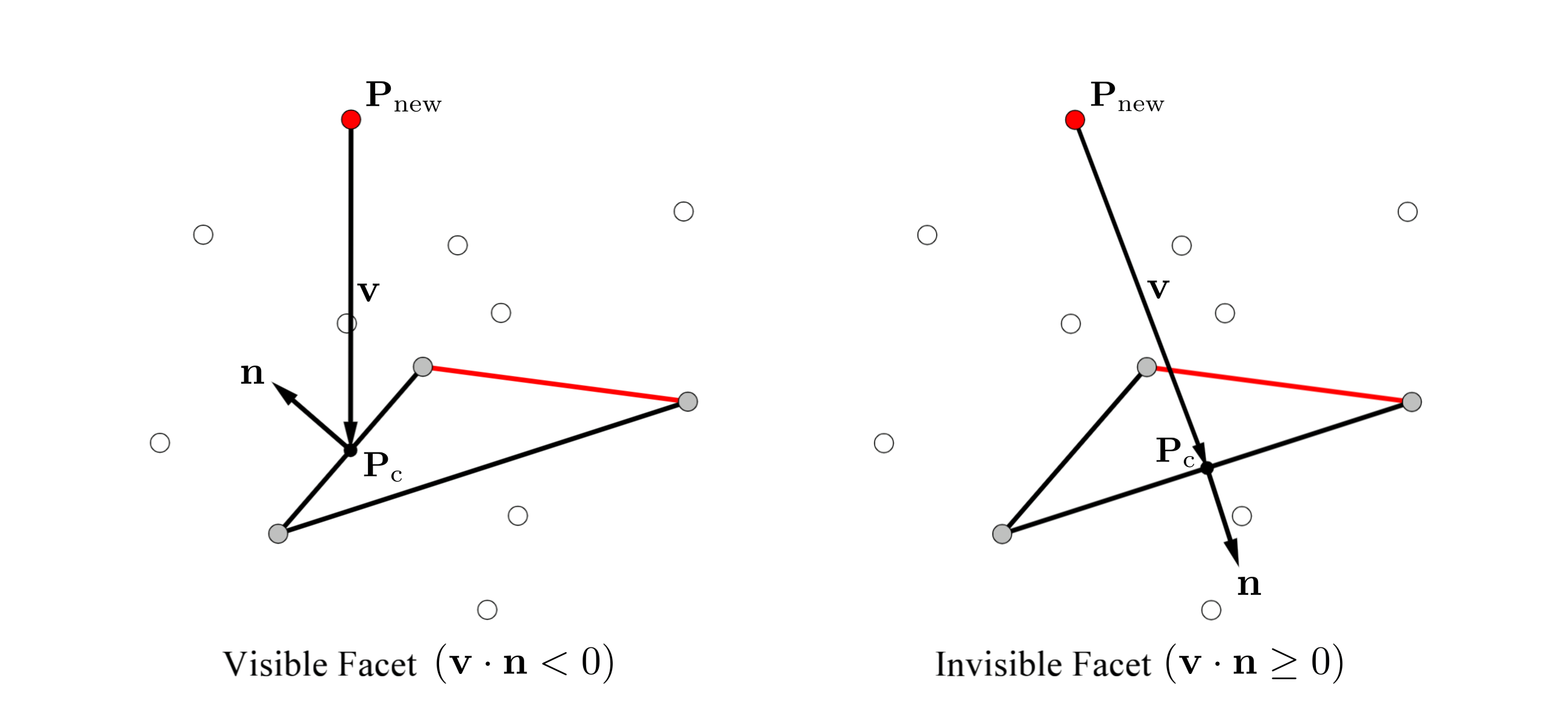
For convex hull computation applicable to high dimensions, the pivoting method [3] and Quickhull [4] are known as representative approaches. In implementations that ensure robustness against inputs with numerical errors or degenerate configurations, these algorithms can in-cur increased computational cost due to exact predicates and additional handling.
Convex hull computation is part of the fundamental problem set in high-dimensional computational geometry, and textbooks systematically organize problems such as convex hulls, halfspace intersection, and arrangements [19].
As existing methods for high-dimensional visualization, there are approaches based on projection to lowerdimensional spaces. Cook et al. provide an overview of methods and design issues for exploring and presenting high-dimensional information via 2D projections [7]. Dimensional stacking has also been surveyed as a class of visualization techniques that assigns each dimension to a nested 2D layout [13].
These works mainly survey visualization techniques. In contrast, on the implementation side, architectures and frameworks for high-dimensional visualization have also been proposed. For mesh-based approaches, a GPUbased 4D visualization architecture has been proposed [6] and discussed from the viewpoint of rendering and visualization of 4D shapes. As a software framework for computations on convex polyhedra, “polymake” has been reported [11]. It provides visualization, exemplified by Schlegel diagrams, together with the underlying algorithmic processing. However, these prior examples differ in scope from the unified environment targeted in this paper, which aims to integrate not only visualization but also other processing in an interactive manner.
For Boolean operations on 3D meshes, methods based on intersection resolution and spatial partitioning have been reported; Zhou et al. present a unified framework that handles union, intersection, and difference based on cell decomposition and extraction using winding number vectors [26]. In the 3D setting, implementation examples of interactive Boolean operations have also been reported [5]. CGAL adopts a design policy that emphasizes geometric robustness [9]. Under this policy, CGAL and related libraries provide set operations in 2D and 3D, exemplified by Nef polyhedra, whereas implementation reports of Boolean operations on explicit boundary meshes in 4D and higher dimensions are limited.
For set operations in 4D and higher dimensions, libraries for high-dimensional computation based on polyhedral representations have been proposed [25]. However, these assume representations based on halfspace con-straints or cell decompositions, rather than explicit boundary meshes. They also typically assume offline computation with exact arithmetic, and implementation reports aimed at interactive operating environments remain limited.
In physical simulation, non-rigid body simulation based on XPBD has been reported in 3D space [16], and there are also studies that handle rigid bodies in 4D and higher dimensions [23]. However, reports whose primary goal is to visualize non-rigid objects in 4D and higher dimensions and handle them interactively remain limited.
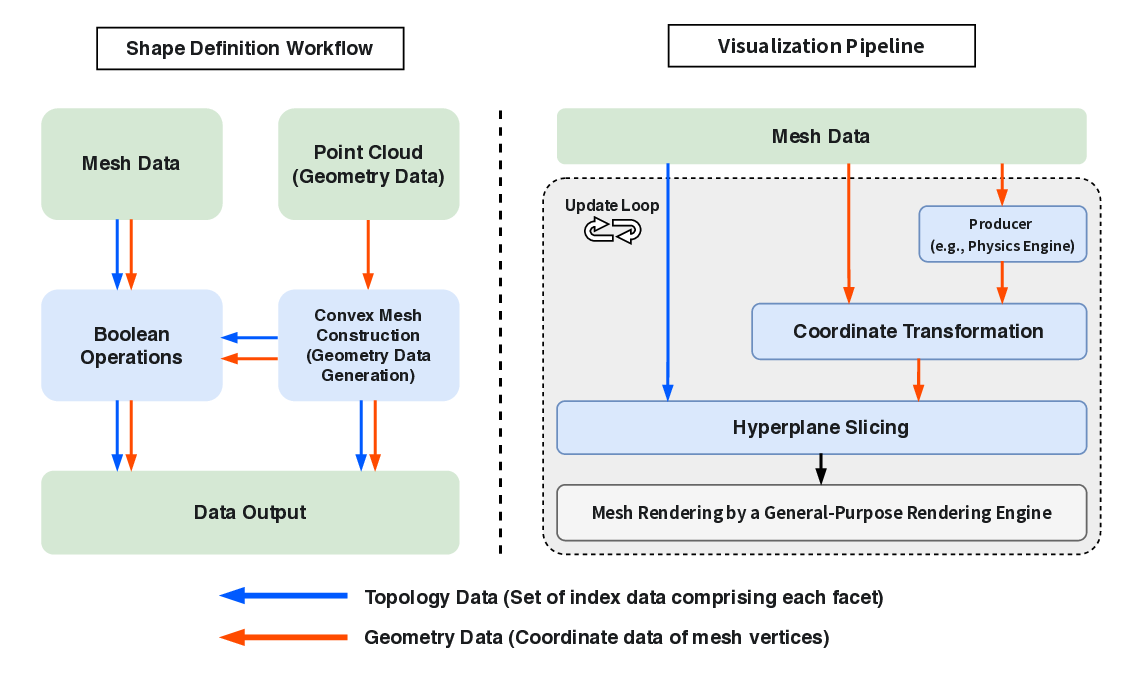
3 Proposed Method This section describes the technical details of the proposed architecture. We first provide an overview of the overall architecture, and then describe in detail the algorithms that constitute each function and their implementations.
As shown in Fig. 1, the overall structure and data flow of the architecture consist of mul
This content is AI-processed based on open access ArXiv data.