Graph Neural Networks (GNNs) have become indispensable in critical domains such as drug discovery, social network analysis, and recommendation systems, yet their black-box nature hinders deployment in scenarios requiring transparency and accountability. While Shapley value-based methods offer mathematically principled explanations by quantifying each component's contribution to predictions, computing exact values requires evaluating $2^n$ coalitions (or aggregating over $n!$ permutations), which is intractable for real-world graphs. Existing approximation strategies sacrifice either fidelity or efficiency, limiting their practical utility. We introduce QGShap, a quantum computing approach that leverages amplitude amplification to achieve quadratic speedups in coalition evaluation while maintaining exact Shapley computation. Unlike classical sampling or surrogate methods, our approach provides fully faithful explanations without approximation trade-offs for tractable graph sizes. We conduct empirical evaluations on synthetic graph datasets, demonstrating that QGShap achieves consistently high fidelity and explanation accuracy, matching or exceeding the performance of classical methods across all evaluation metrics. These results collectively demonstrate that QGShap not only preserves exact Shapley faithfulness but also delivers interpretable, stable, and structurally consistent explanations that align with the underlying graph reasoning of GNNs. The implementation of QGShap is available at https://github.com/smlab-niser/qgshap.
Graph neural networks (GNNs) have gained widespread use for learning from graph-structured data in critical applications such as molecular chemistry (Reiser et al., 2022), social network analysis (Li et al., 2023), and recommendation systems (Wu et al., 2022). They excel at capturing complex relationships and patterns within interconnected data (Joshi & Mishra, 2022), enabling breakthroughs in areas like drug discovery, social network analysis, and recommendation systems. However, despite their success, GNNs often function as 'black boxes', making it difficult for users and stakeholders to understand how they arrive at their decisions (Agarwal et al., 2023). This opacity poses significant challenges in domains, where transparency, trust, and accountability are essential. Additionally, the complexity of GNN architectures (Gilmer et al., 2017;Kipf & Welling, 2017;Veličković et al., 2018) and the diversity of graph data further complicate efforts to interpret their predictions.
Building on recent advances in GNN explainability, researchers have moved beyond node and edge-level explanation methods, such as GNNExplainer (Ying et al., 2019), PGExplainer (Luo et al., 2020), and GraphLIME (Huang et al., 2022), toward approaches that capture more complex structural patterns in graphs. While GNNExplainer and PGExplainer use gradient and perturbation-based techniques to identify important components, they often produce explanations that are faithful but unstable, especially on complex benchmarks (Agarwal et al., 2023). Surrogate learning methods like GraphLIME aim to explain local feature relationships, but they still explain only the node features. More recent work, such as SubgraphX (Yuan et al., 2021), leverages Shapley values (Kuhn & Tucker, 1953) combined with Monte Carlo Tree Search (Silver et al., 2017) to identify entire explanatory subgraphs. This shift enables explanations that are both more faithful and interpretable at a higher semantic level, moving the field toward more robust and meaningful forms of interpretability.
Motivated by this shift toward subgraph-level reasoning, Shapley value-based (Lundberg & Lee, 2017) explainability methods have emerged as the principled foundation underlying such scoring, offering a mathematically rigorous way to quantify how each node or subgraph contributes to a model’s prediction (Yuan et al., 2021;Akkas & Azad, 2024;Duval & Malliaros, 2021). By aggregating the marginal impact of each component across all possible coalitions, Shapley values provide fairness and completeness in attribution (Lundberg & Lee, 2017). Yet, the very strength of this formulation -its exhaustive consideration of all 2 n combinations, renders it computationally prohibitive for real-world graphs. Classical approaches have sought to approximate these values through sampling, Monte Carlo estimation, or surrogate modeling, but such strategies unavoidably trade off either fidelity or efficiency (Yuan et al., 2021;Duval & Malliaros, 2021;Akkas & Azad, 2024;Muschalik et al., 2025).
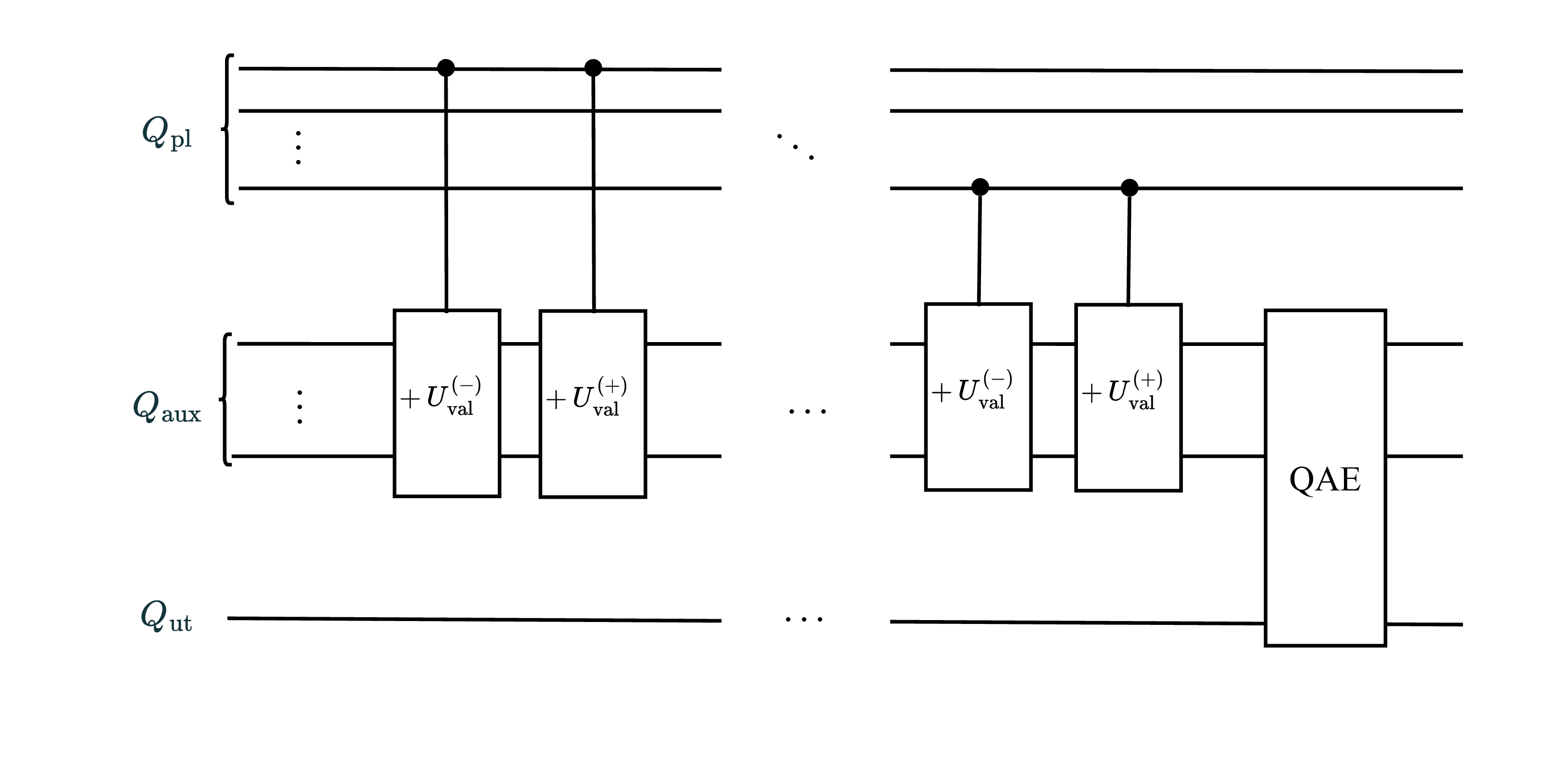
To move beyond this bottleneck while retaining Shapley’s axiomatic benefits, recent advances in quantum computing have introduced algorithms that exploit amplitude amplification to achieve quadratic speedups for combinatorial evaluation tasks, including subset and coalition scoring (Montanaro, 2015;Burge et al., 2025). Building on these developments, we propose QGShap for GNN explainability that leverages amplitude amplification to accelerate coalition evaluation, while maintaining exact Shapley computation. Empirical evaluations on synthetic and small real-world datasets demonstrate that our method achieves exact Shapley faithfulness, suggesting that quantum algorithms can play a transformative role in scaling the explainability of GNNs.
We introduce QGShap, demonstrating that quantum amplitude-estimation techniques can accelerate brute-force Shapley value computation for GNN explanations, achieving faithful, theoretically grounded node attributions with quadratic query speedup over classical approaches.
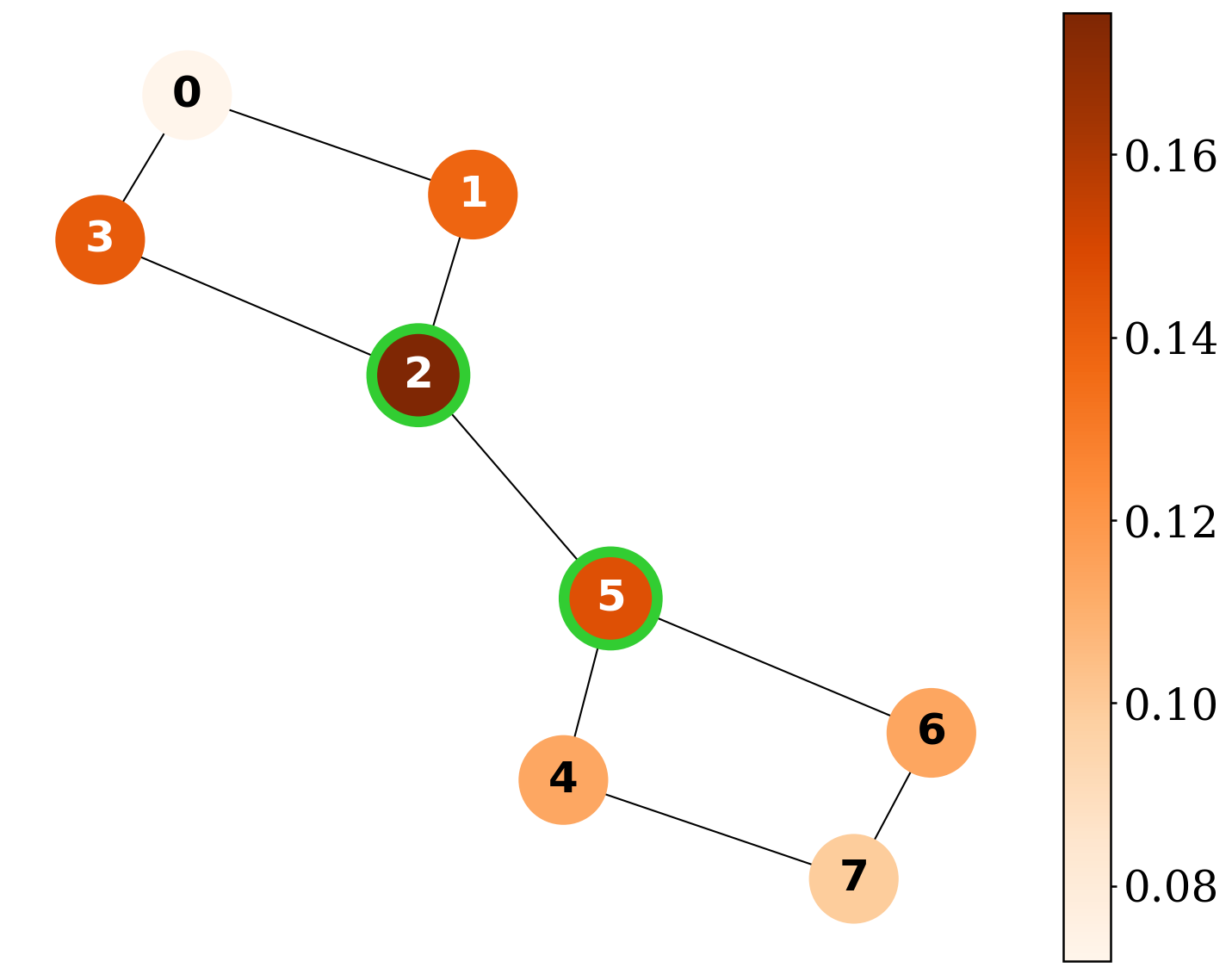
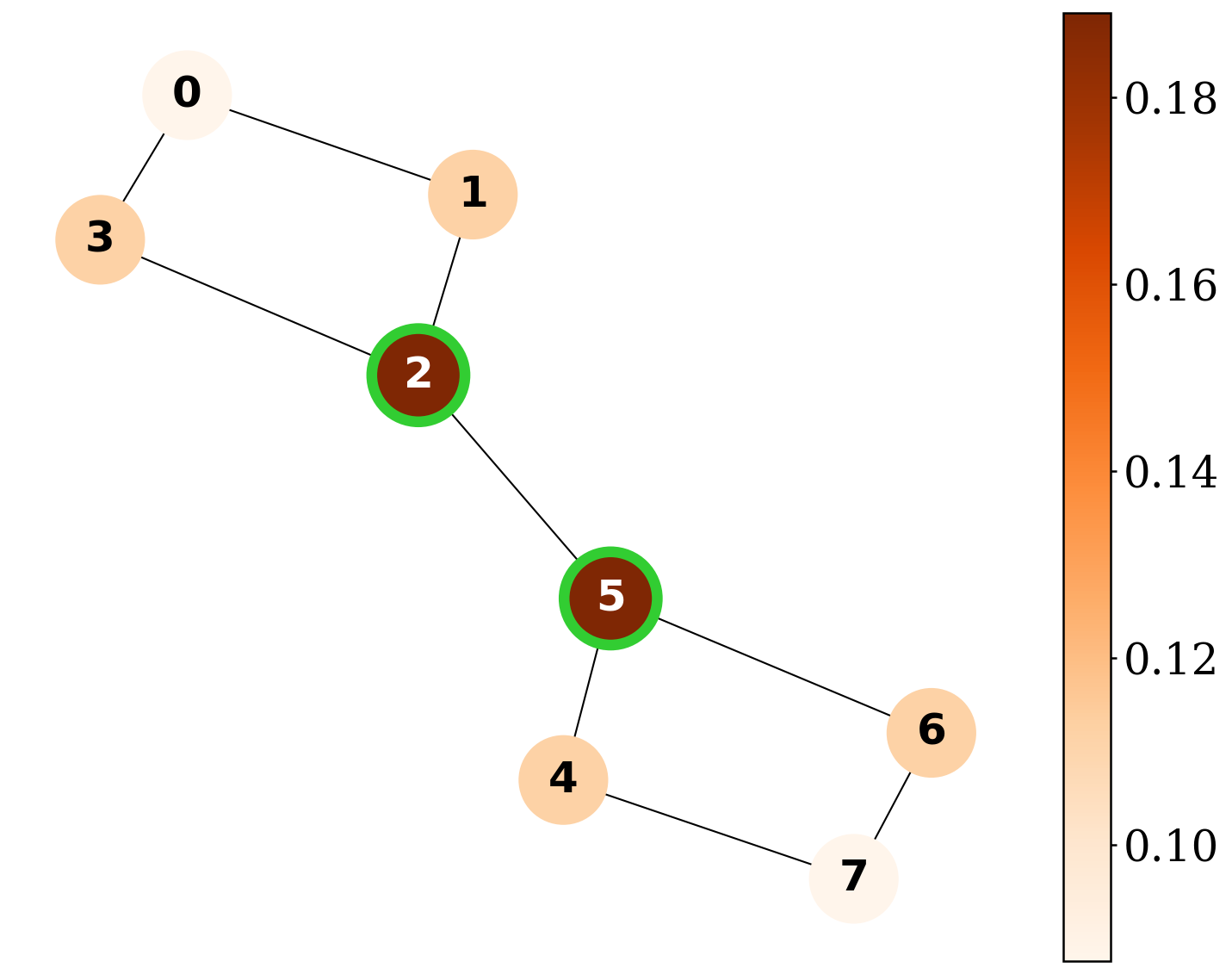
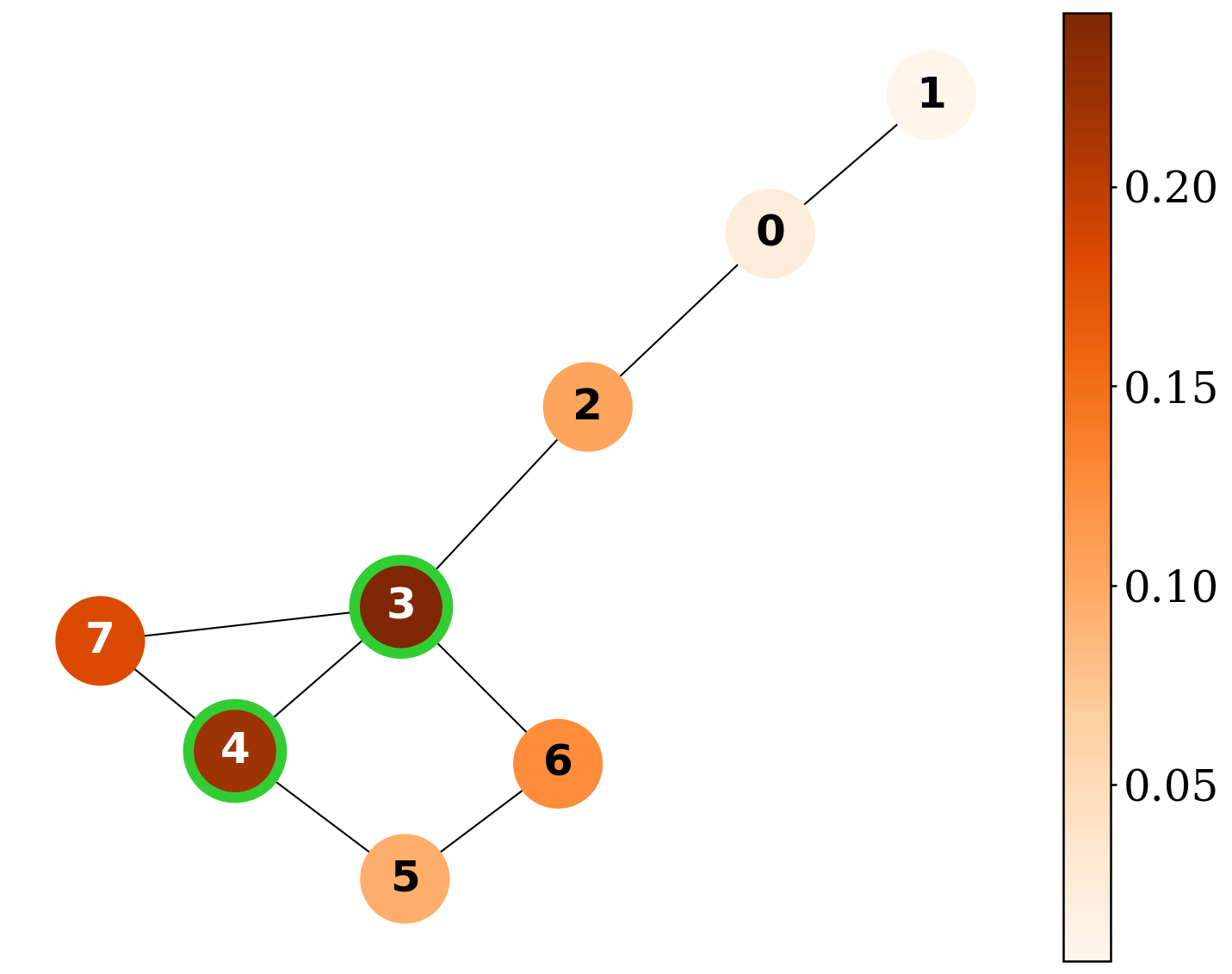
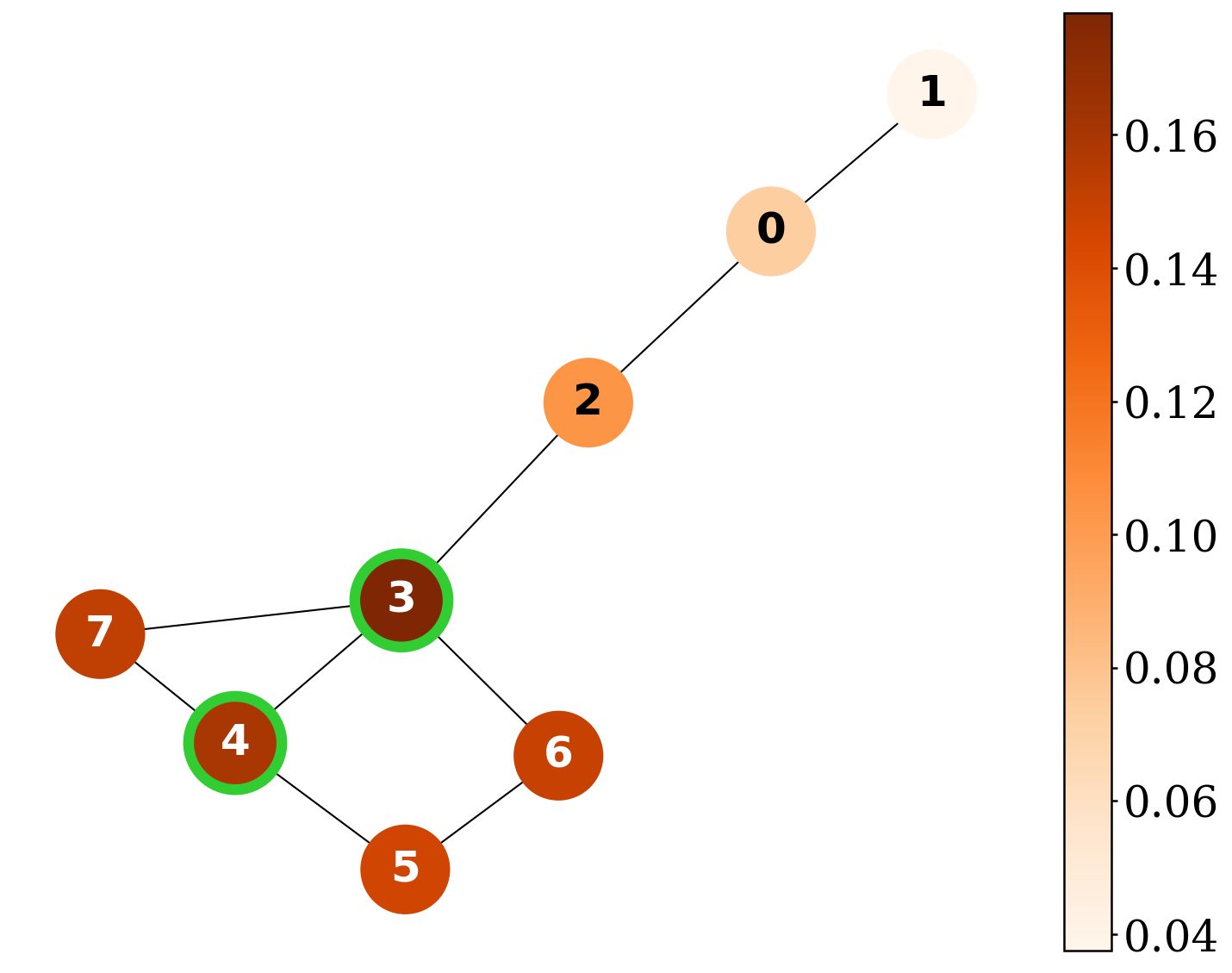
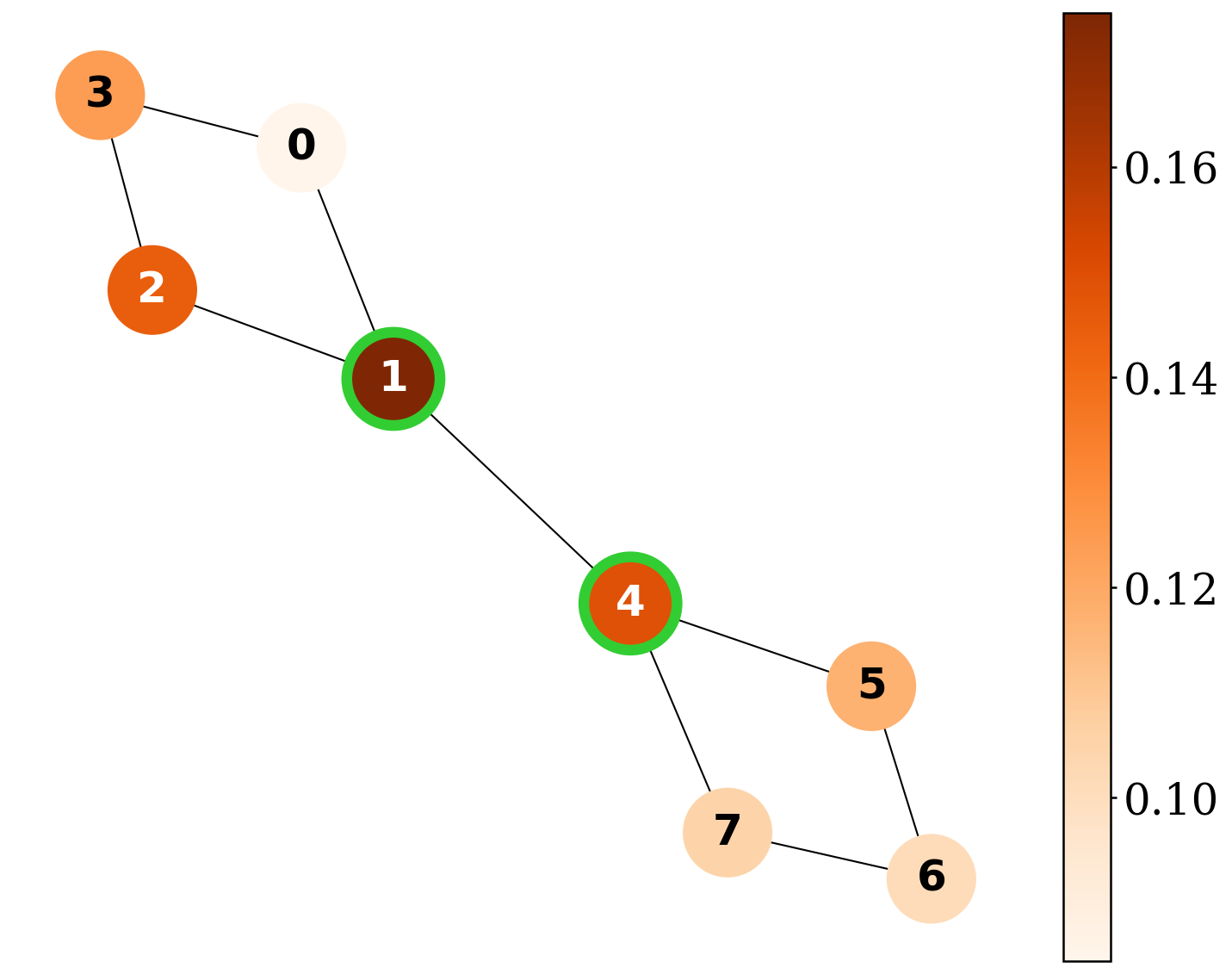
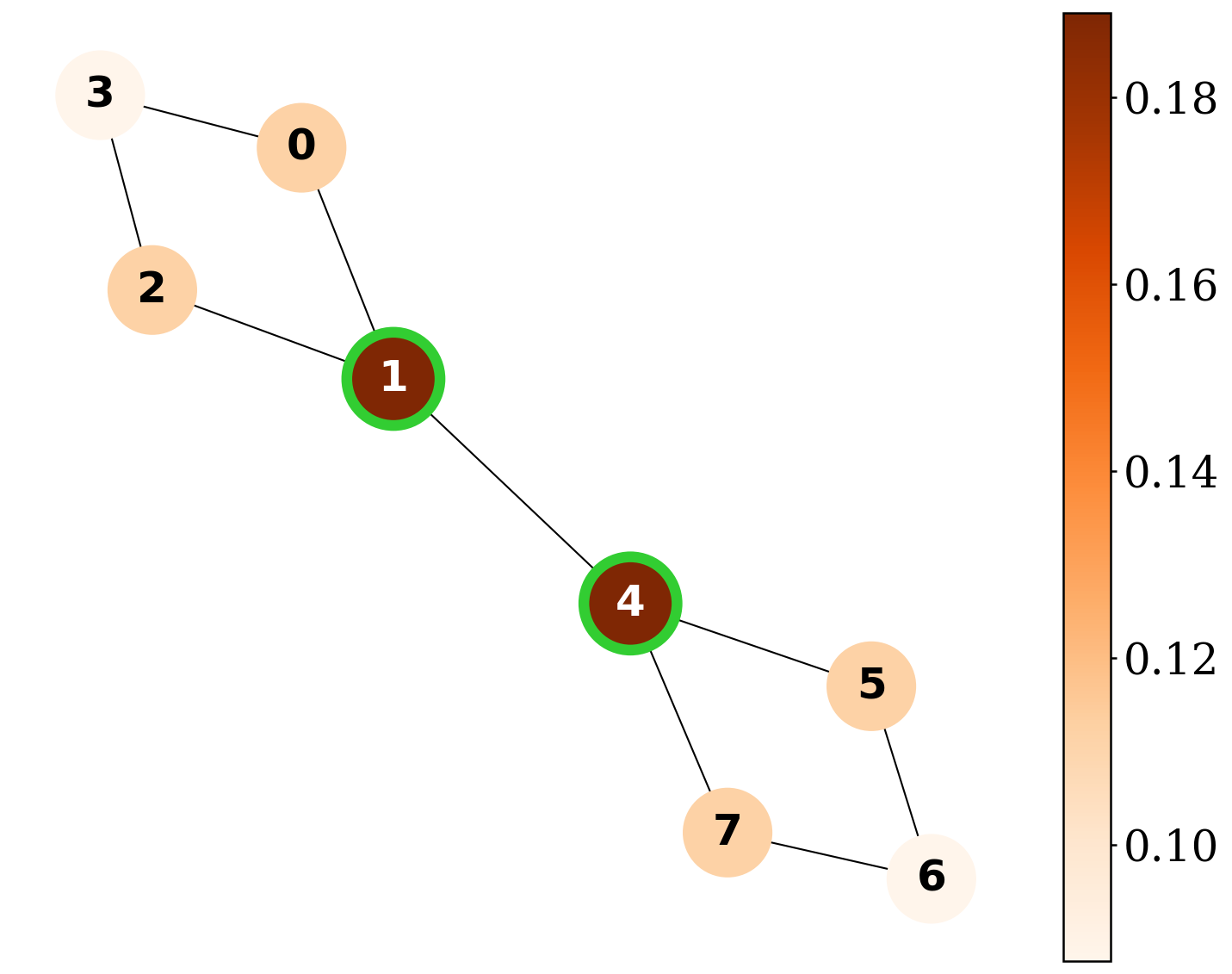
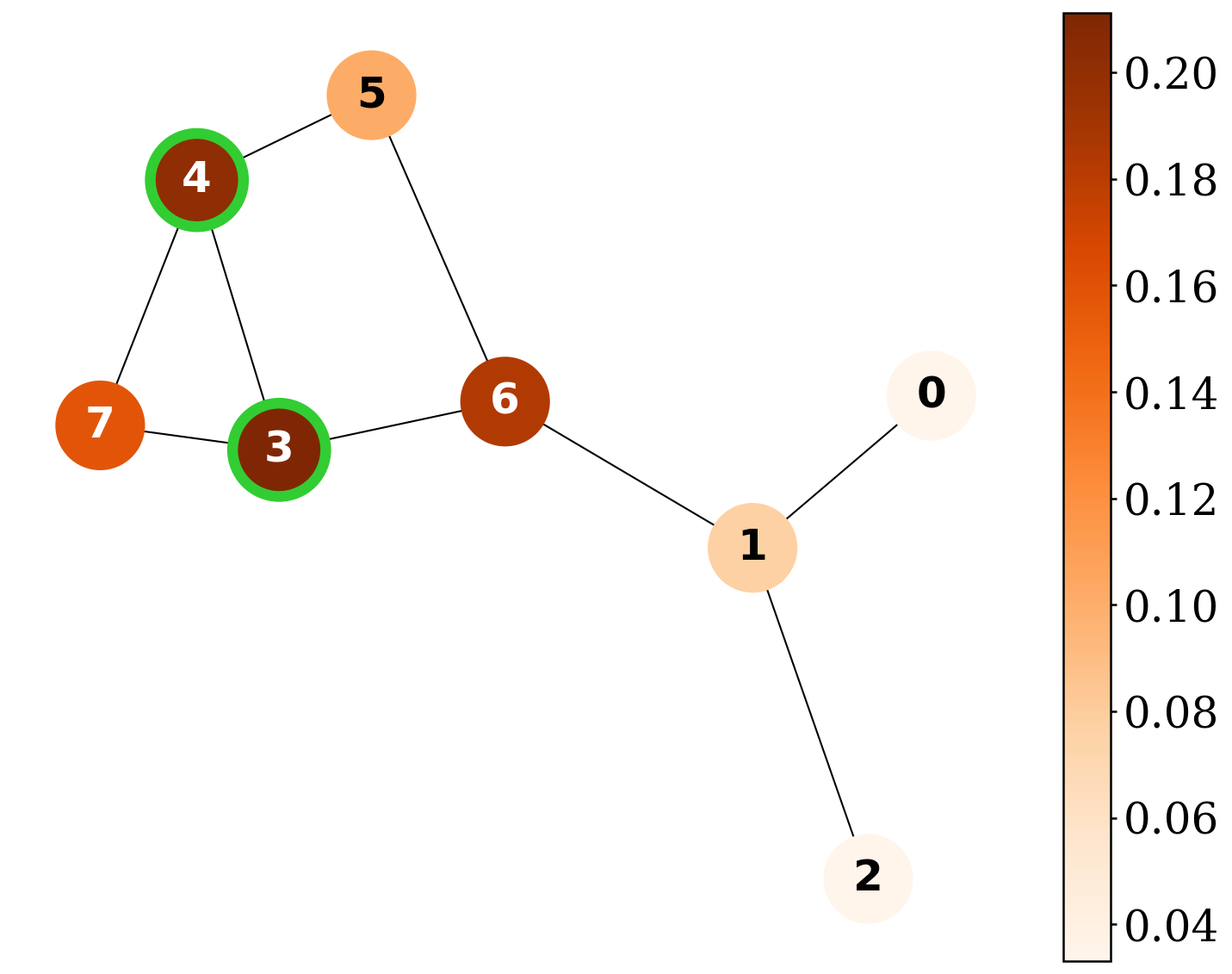
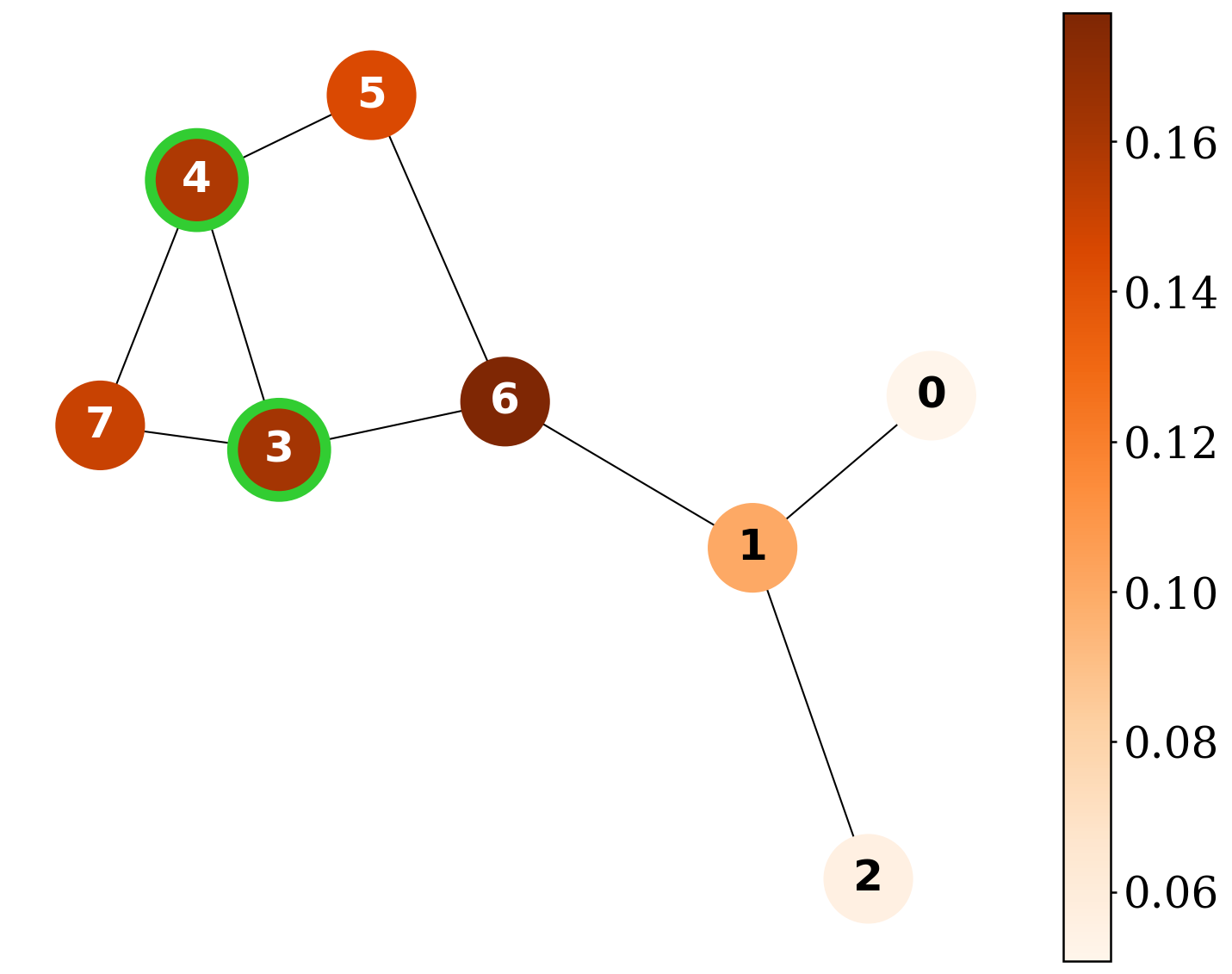
QGShap provides exact Shapley-based explanations and surpasses existing explainers on explanation-quality metrics across synthetic graph benchmarks.
GNNs have established themselves as highly effective frameworks for learning and reasoning over complex structured data (Wu et al., 2021). Despite their remarkable predictive capabilities and widespread success across numerous domains, the internal decision-making mechanisms of GNNs often remain largely opaque (Agarwal et al., 2023). Early research in GNN explainability focused on attributing importance to individual nodes, edges, or features through gradient-based techniques such as Saliency Analysis (SA) (Zeiler & Fergus, 2014), Class Activation Mapping (CAM) (Zhou et al., 2016), and Guided Backpropagation (Guided BP) (Springenberg et al., 2015); decomposition-based methods like Layer-wise Relevance Propagation (LRP) (Schwarzenberg et al., 2019) and Excitation Bac
This content is AI-processed based on open access ArXiv data.