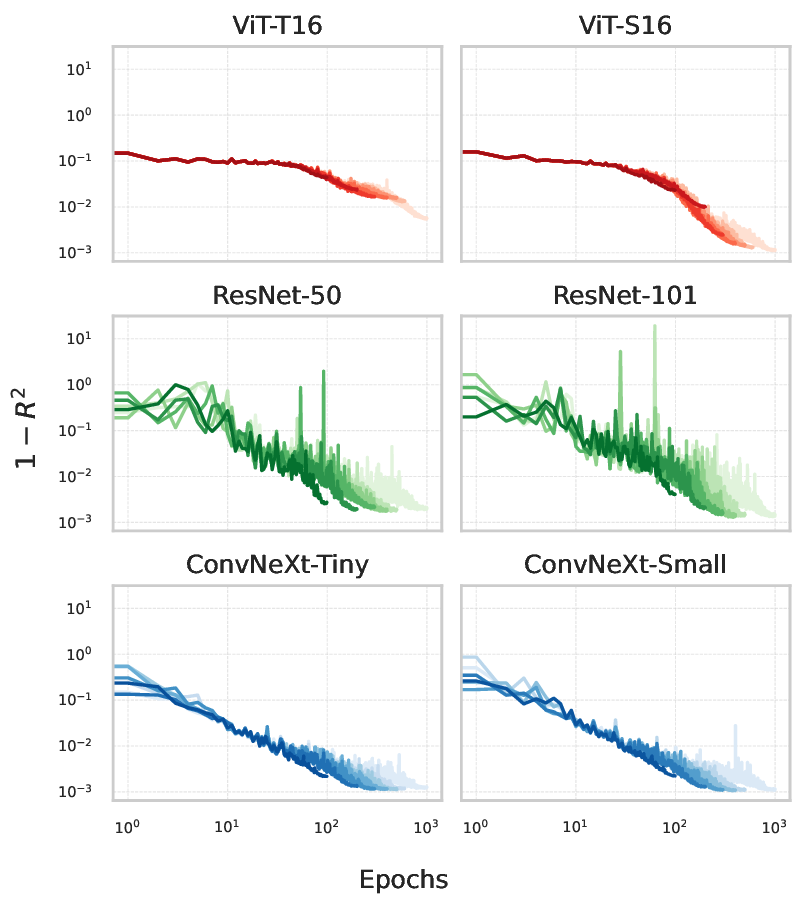
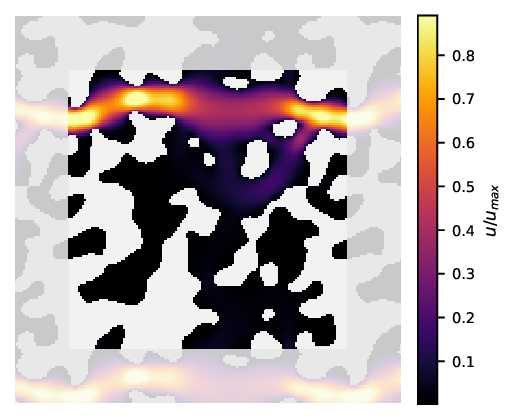
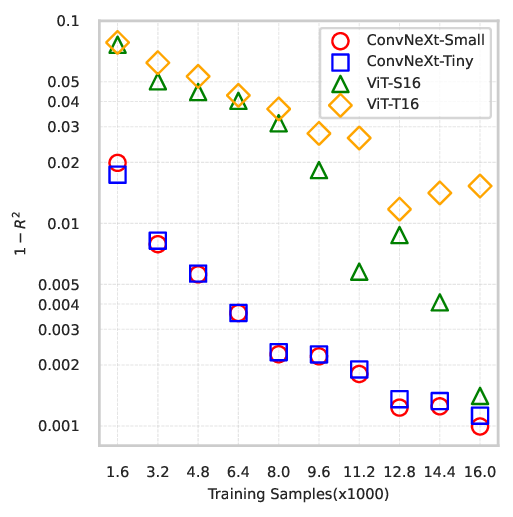
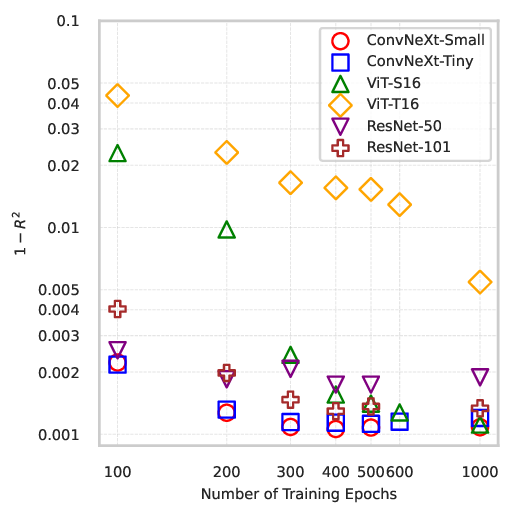
Permeability is a central concept in the macroscopic description of flow through porous media, with applications spanning from oil recovery to hydrology. Traditional methods for determining the permeability tensor involving flow simulations or experiments can be time consuming and resource-intensive, while analytical methods, e.g., based on the Kozeny-Carman equation, may be too simplistic for accurate prediction based on pore-scale features. In this work, we explore deep learning as a more efficient alternative for predicting the permeability tensor based on two-dimensional binary images of porous media, segmented into solid ($1$) and void ($0$) regions. We generate a dataset of 24,000 synthetic random periodic porous media samples with specified porosity and characteristic length scale. Using Lattice-Boltzmann simulations, we compute the permeability tensor for flow through these samples with values spanning three orders of magnitude. We evaluate three families of image-based deep learning models: ResNet (ResNet-$50$ and ResNet-$101$), Vision Transformers (ViT-T$16$ and ViT-S$16$) and ConvNeXt (Tiny and Small). To improve model generalisation, we employ techniques such as weight decay, learning rate scheduling, and data augmentation. The effect of data augmentation and dataset size on model performance is studied, and we find that they generally increase the accuracy of permeability predictions. We also show that ConvNeXt and ResNet converge faster than ViT and degrade in performance if trained for too long. ConvNeXt-Small achieved the highest $R^2$ score of $0.99460$ on $4,000$ unseen test samples. These findings underscore the potential to use image-based neural networks to predict permeability tensors accurately.
Predicting the transport properties of porous media is crucial to many industries, such as oil recovery, groundwater management, and CO 2 subsurface storage [1,2]. Slow, steady flow through porous media is described macroscopically by Darcy's law:
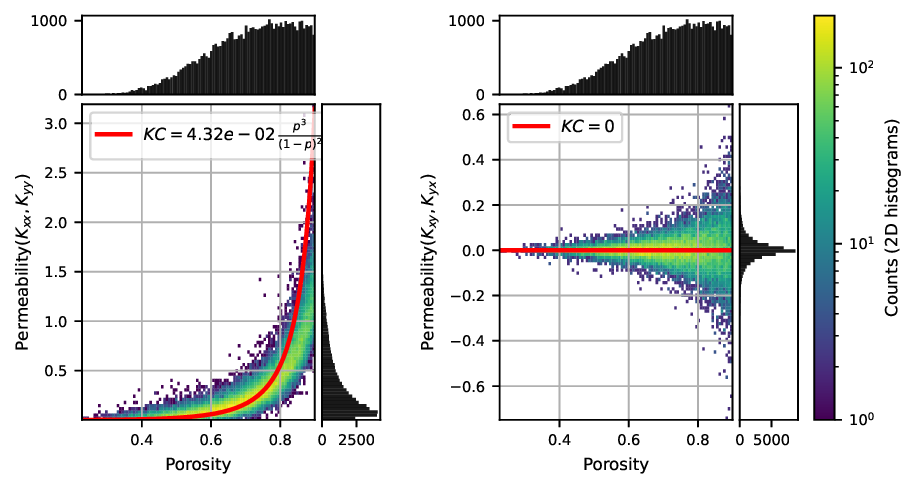
where u is the average fluid velocity, µ is the fluid viscosity, p is the pressure, and f is a body force such as that due to gravity. The permeability tensor K is a purely geometric quantity that encodes small-scale structure and relates pressure gradients to flow rates. In effect, it quantifies how easily a fluid flows through a porous medium. Low permeability is often associated with complex, tortuous structures, while high permeability indicates more open and direct flow paths.
Determining the permeability accurately is not straightforward. Traditionally, experiments or simulations of the flow through the pore-scale microstructure are needed, and these can be time-consuming and resourceintensive. Theoretical estimates, such as those based on the Kozeny-Carman equation, tend to be less accurate on complex structures because they do not incorporate key geometric information [1,3]. Pore-network models [4] provide a computationally cheaper alternative, but their accuracy depends strongly on how faithfully the pore geometry and connectivity are represented; simplified network constructions often lead to reduced predictive accuracy. The inaccuracy of theoretical estimates and the fact that experimental and numerical measurements are demanding and must be done on a case-by-case basis, motivate the search for alternative, efficient and accurate methods.
The success of convolutional neural networks (CNNs) in image recognition [5], scaled with AlexNet in 2012 [6] and extended by ResNet in 2015 [7], demonstrated the potential for data-driven feature extraction. Later, the transformer architecture [8] enabled the Vision Transformer (ViT) [9], which models long-range dependencies using self-attention and tokenization of images instead of convolutions. More recently, ConvNeXt [10] has bridged CNNs and transformers by incorporating architectural refinements such as patchification, large kernels, and inverted bottlenecks, along with modern training techniques. These changes enable convolution-based models to achieve performance comparable to transformers.
In recent years, image-based deep learning has emerged as a promising alternative for predicting permeability. The accuracy of the prediction is often measured with the coefficient of determination:
where we denote the Frobenius norm of a d × d matrix A as ||A|| F = d i=1 d j=1 A ij . K is the predicted permeability tensor, K is the target permeability tensor, and K is the mean of the target permeability values. Araya-Polo et al. [11] combined high-resolution two-dimensional (2D) images obtained from thin sections of core plugs with laboratory measurements of their permeabilities. They achieved R 2 = 0.9582 on thin-section subsamples, and R 2 = 0.7967 when evaluating across larger spans of the core plug scans. Graczyk and Matyka [12] applied CNNs to predict porosity, permeability, and tortuosity from synthetic 2D Poisson porous media, where the flow-dependent properties were determined for a single flow direction using Lattice-Boltzmann simulations. Takbiri et al. [13] adopted a U-Net [14] architecture to predict velocity fields in simple geometric domains (ellipses and rectangles) and derived permeability from them. On a test set with discs as obstacles their model achieved the highest R 2 = 0.98 on the K xx component. Zhai et al. [15] compared ConvNeXt, ViT, DensNet [16], and ResNet in a single flow direction for permeability prediction. They used 2D synthetic images and a finite-element solver to obtain the flow fields. On a test set of 200 images, their ConvNeXt achieved the highest accuracy with R 2 = 0.9667. Kashefi and Mukerji [17] applied the Vision Mamba [18] to single direction permeability prediction in 3D, achieving R 2 = 0.9969 on 170 synthetic test samples. Their total dataset consisted of 1, 692 samples with a porosity range of [0.125, 0.200], and their flow fields were based on Lattice-Boltzmann simulations. Avilkin et al. [19] evaluated an XGBoost [20] model using geometric features from 2D slices of synthetic 3D porous structures, using Lattice-Boltzmann simulations to calculate the permeability. Depending on the slice configuration, they reported R 2 scores of 0.79 (single slice), 0.85 (three random slices), and up to 0.91 when using three orthogonal slices.
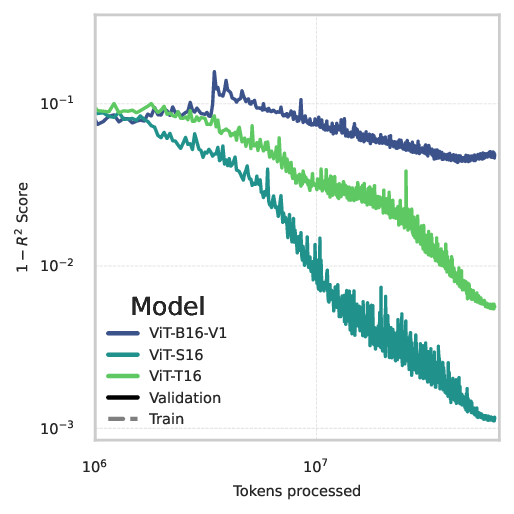
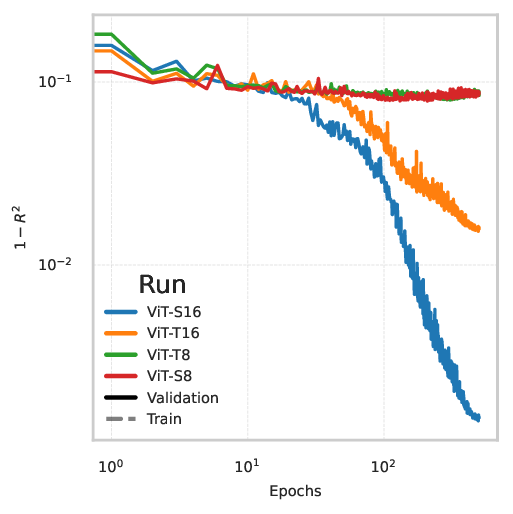
In this work, we evaluate the capability of three architectures-ResNet, ViT, and ConvNeXt-to predict the full permeability tensor of complex 2D porous media samples. As modern deep learning methods typically benefit from larger and more diverse datasets [21], we here increase both the dataset size and the model capacity compared to previous studies, aiming for higher predictive accuracy. In particular, we generate 24, 000 synthetic random porous
This content is AI-processed based on open access ArXiv data.