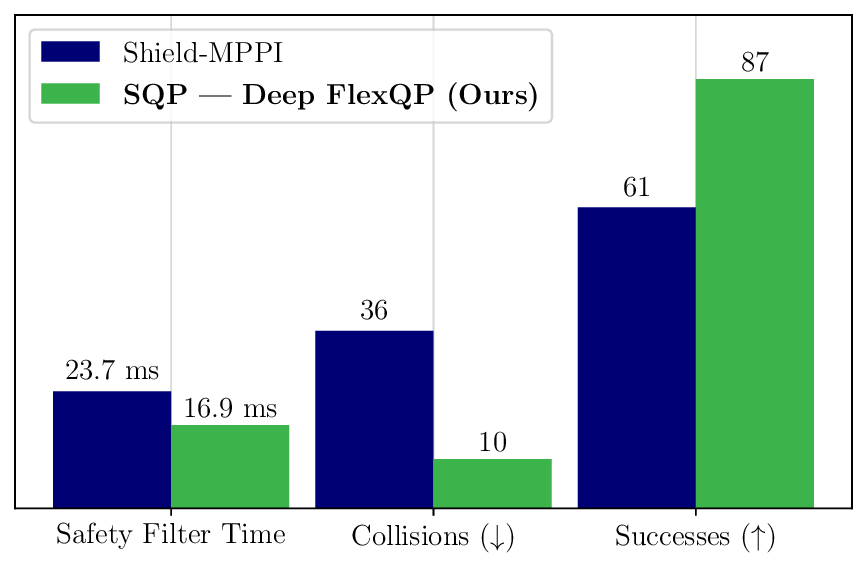
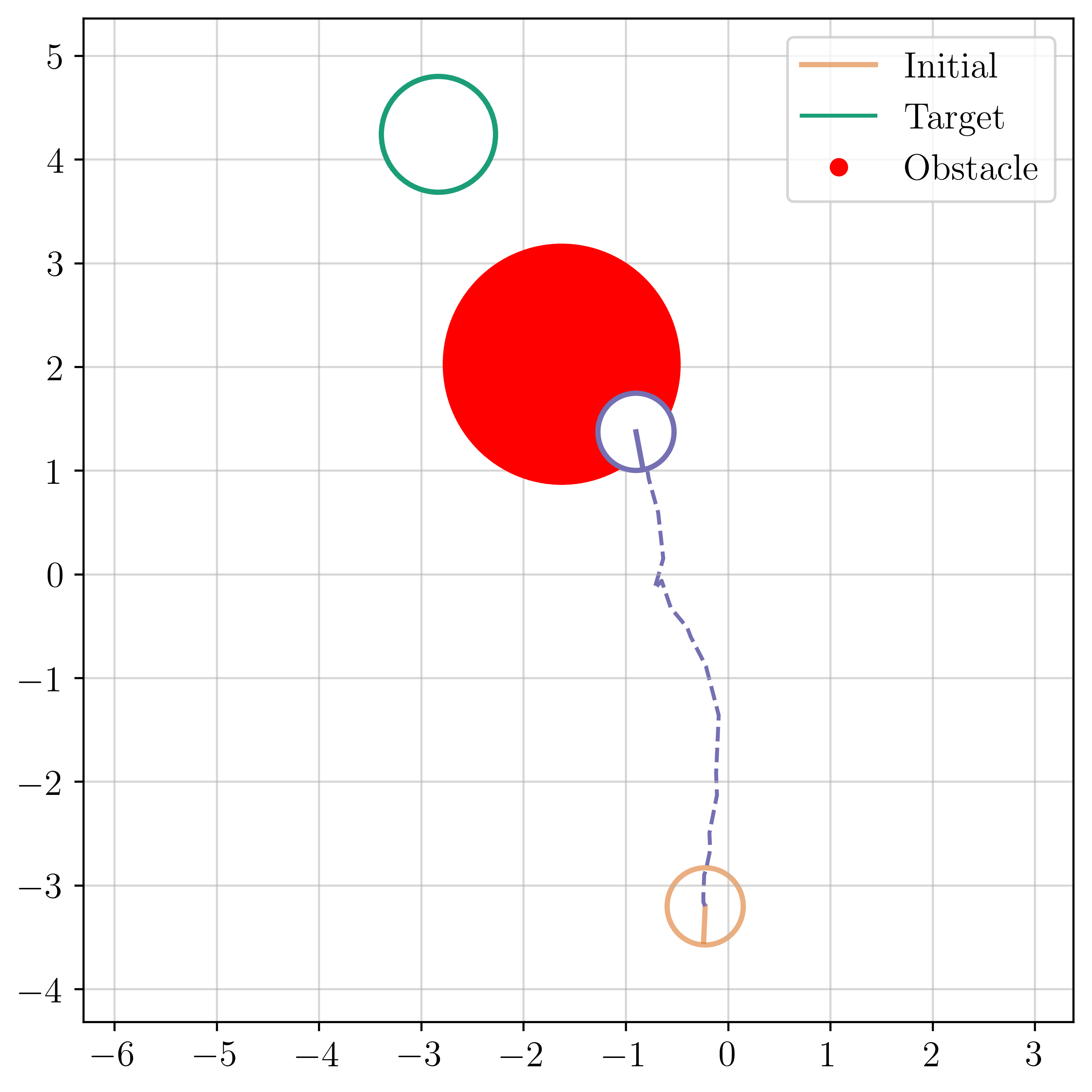
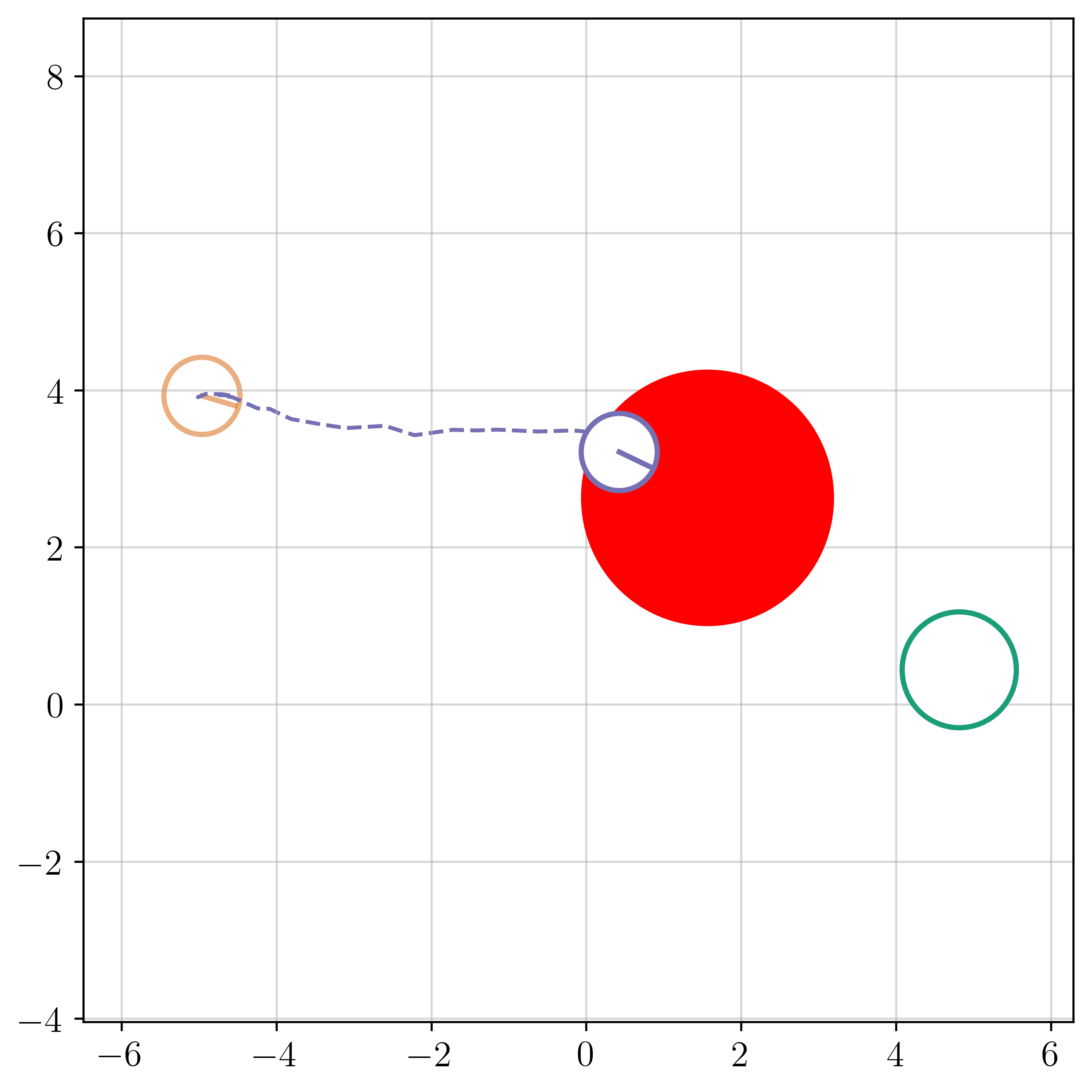
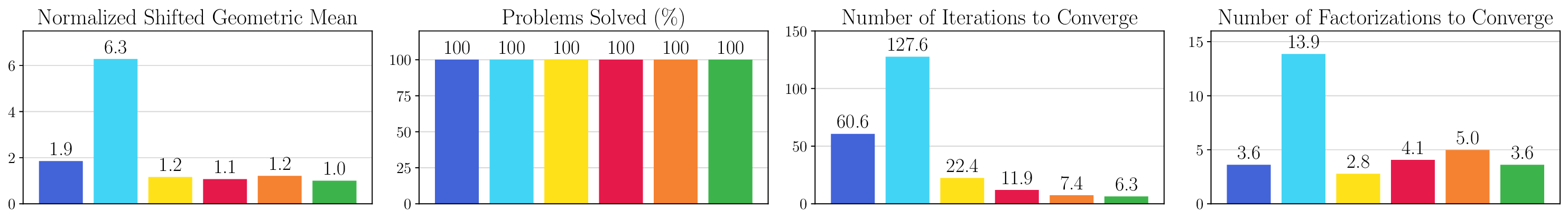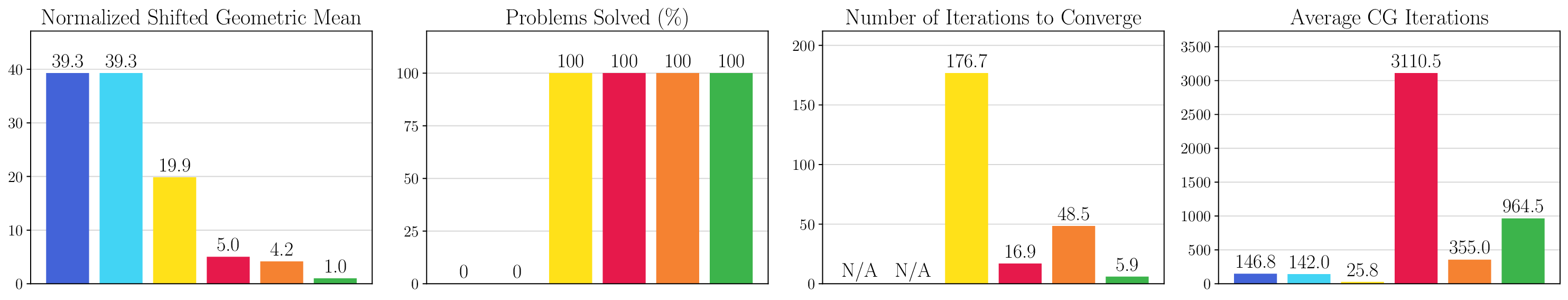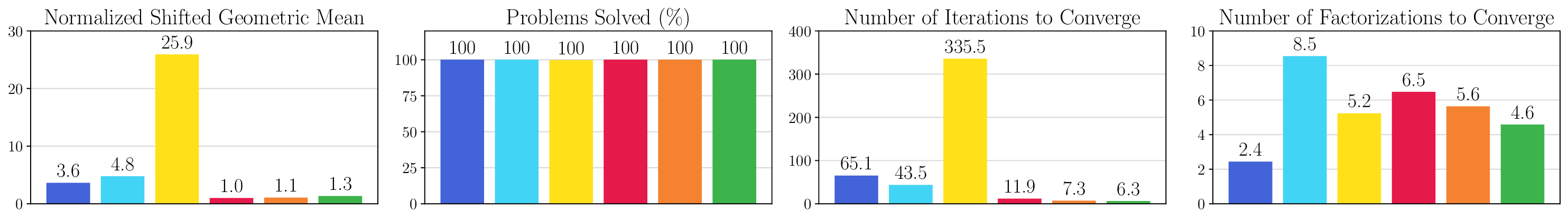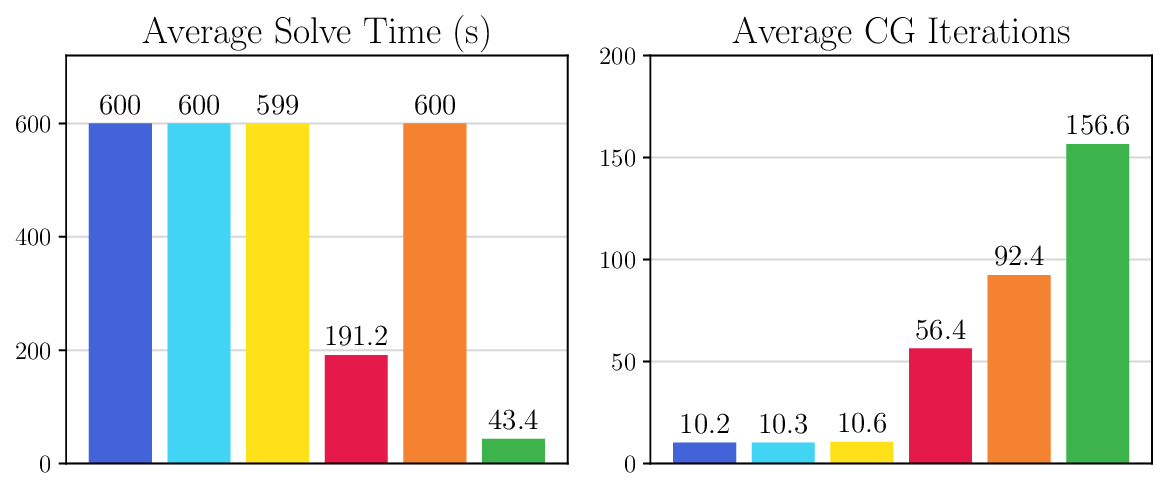We propose an always-feasible quadratic programming (QP) optimizer, FlexQP, which is based on an exact relaxation of the QP constraints. If the original constraints are feasible, then the optimizer finds the optimal solution to the original QP. On the other hand, if the constraints are infeasible, the optimizer identifies a solution that minimizes the constraint violation in a sparse manner. FlexQP scales favorably with respect to the problem dimension, is robust to both feasible and infeasible QPs with minimal assumptions on the problem data, and can be effectively warm-started. We subsequently apply deep unfolding to improve our optimizer through data-driven techniques, leading to an accelerated Deep FlexQP. By learning dimension-agnostic feedback policies for the parameters from a small number of training examples, Deep FlexQP generalizes to problems with larger dimensions and can optimize for many more iterations than it was initially trained for. Our approach outperforms two recently proposed state-of-the-art accelerated QP approaches on a suite of benchmark systems including portfolio optimization, classification, and regression problems. We provide guarantees on the expected performance of our deep QP optimizer through probably approximately correct (PAC) Bayes generalization bounds. These certificates are used to design an accelerated sequential quadratic programming solver that solves nonlinear optimal control and predictive safety filter problems faster than traditional approaches. Overall, our approach is very robust and greatly outperforms existing non-learning and learning-based optimizers in terms of both runtime and convergence to the optimal solution across multiple classes of NLPs.
Nonlinear programming (NLP) is a key technique for both large-scale decision making, where difficulty arises due to the sheer number of variables and constraints, as well as realtime embedded systems, which need to solve many NLPs with similar structure quickly and robustly. Within NLP, quadratic programming (QP) plays a fundamental role as many real-world problems in optimal control (Anderson and Moore, 2007), portfolio optimization (Markowitz, 1952;Boyd et al., 2013Boyd et al., , 2017)), and machine learning (Huber, 1964;Cortes and Vapnik, 1995;Tibshirani, 1996;Candes et al., 2008) can be represented as QPs.
Furthermore, sequential quadratic programming (SQP) methods utilize QP as a submodule to solve much more complicated problems where the objective and constraints may be nonlinear and non-convex, such as in nonlinear model predictive control (Diehl et al., 2009;Rawlings et al., 2020), state estimation (Aravkin et al., 2017), and power grid optimization (Montoya et al., 2019). SQP itself can even be used as a subproblem for solving mixed integer NLPs (Leyffer, 2001) and large-scale partial differential equations (Fang et al., 2023).
However, a common difficulty with SQP methods occurs when the linearization of the constraints results in an infeasible QP subproblem, and a large amount of research has focused on how to repair or avoid these infeasibilities, e.g., (Fletcher, 1985;Izmailov and Solodov, 2012), among others. A significant advantage of SNOPT (Gill et al., 2005), one of the most well-known SQP-based methods, is in its infeasibility detection and reduction handling. These considerations necessitate a fast yet robust QP solver that works under minimal assumptions on the problem parameters.
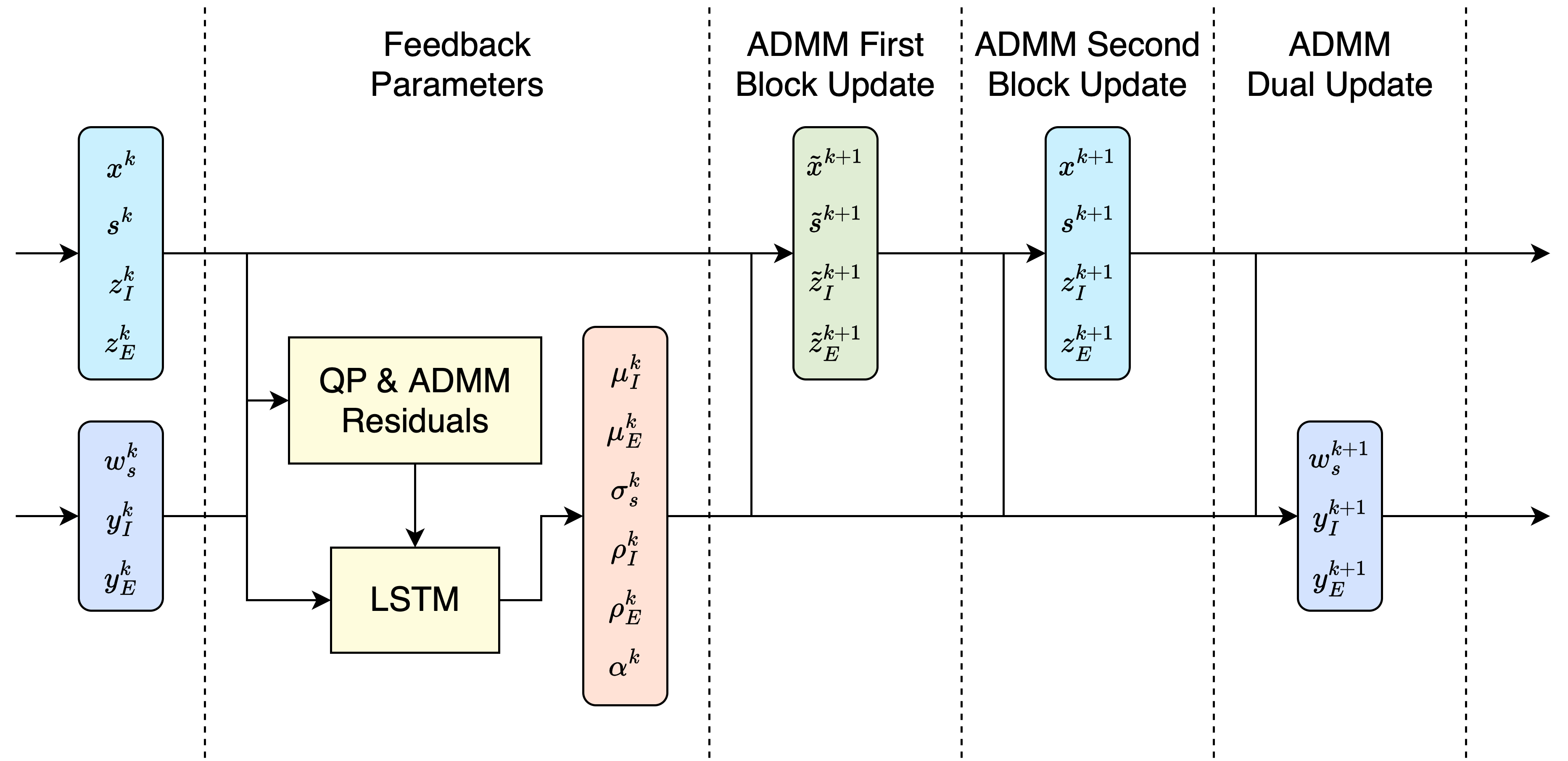
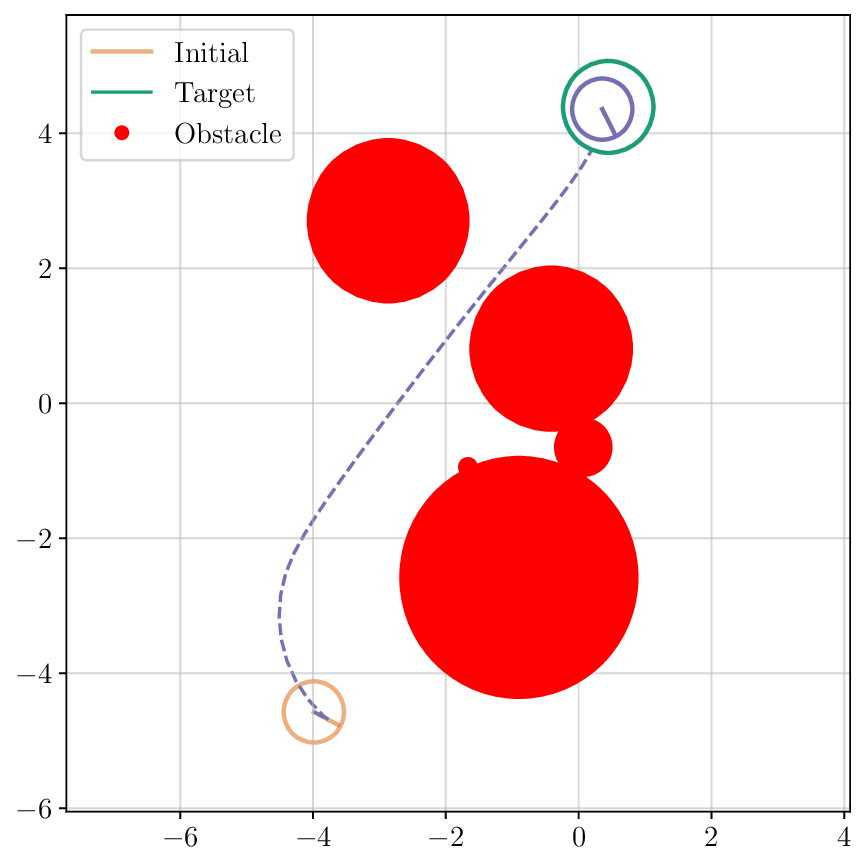
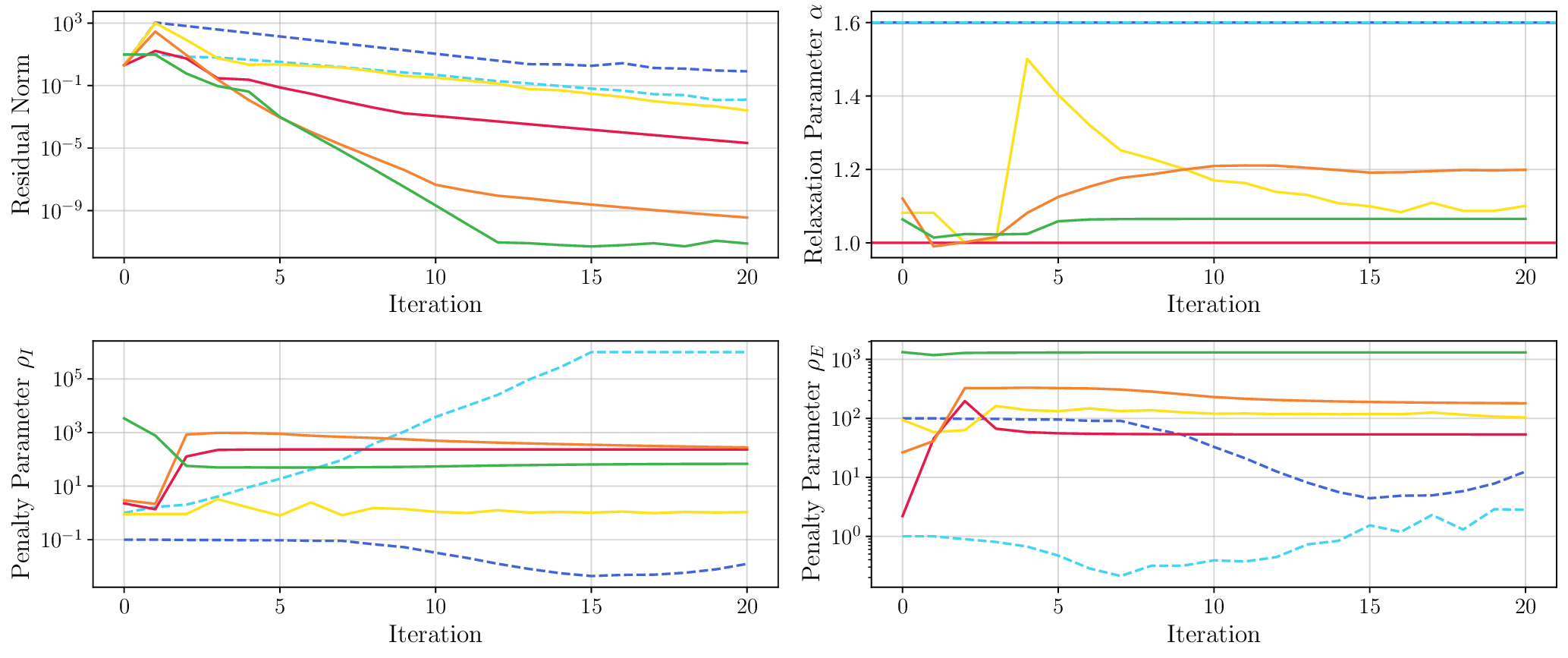
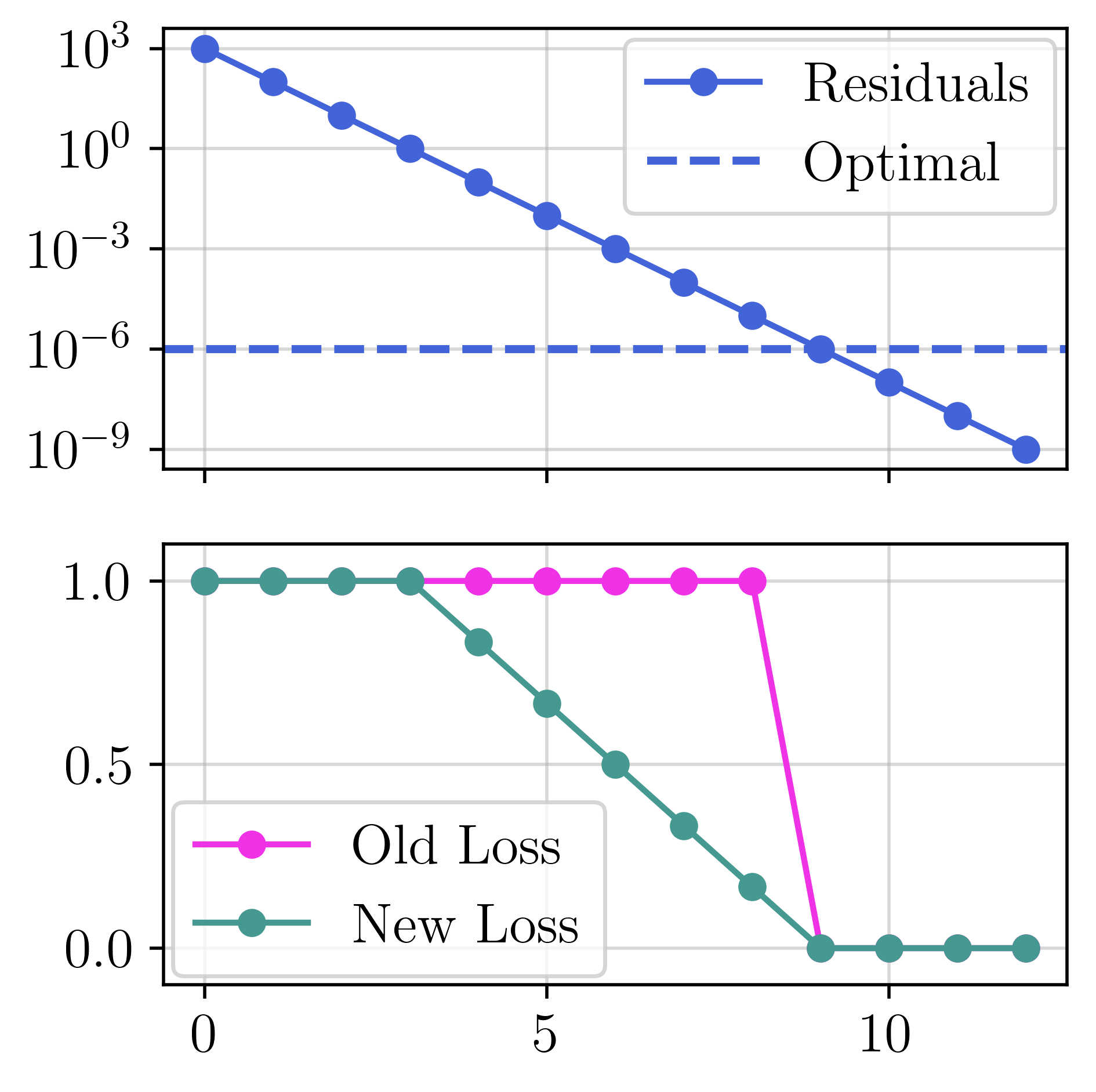
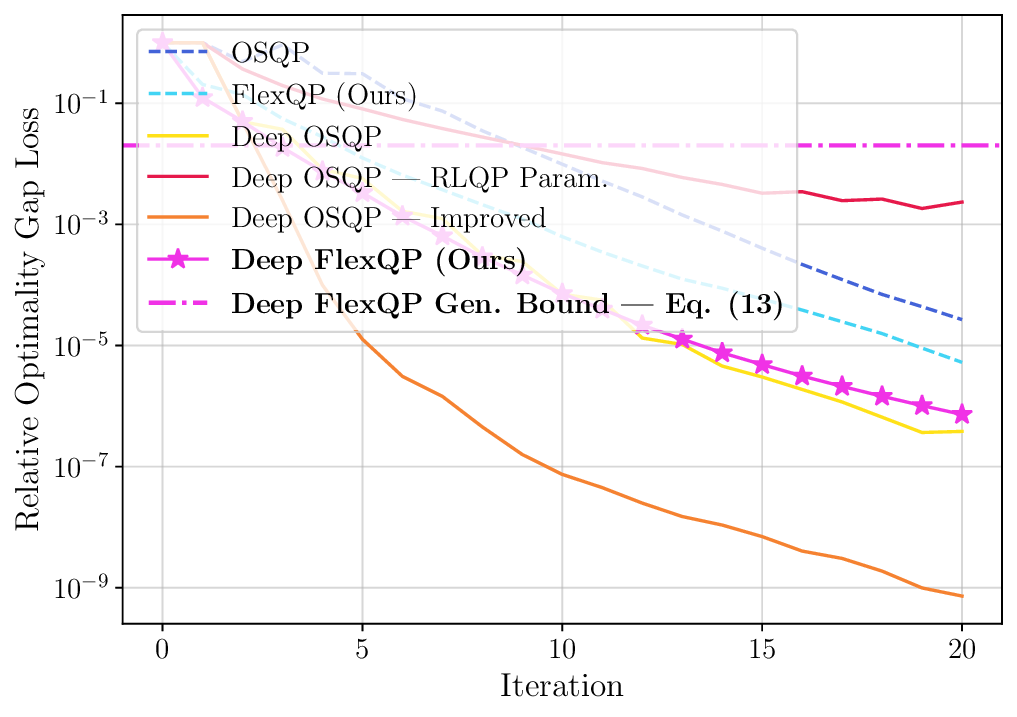
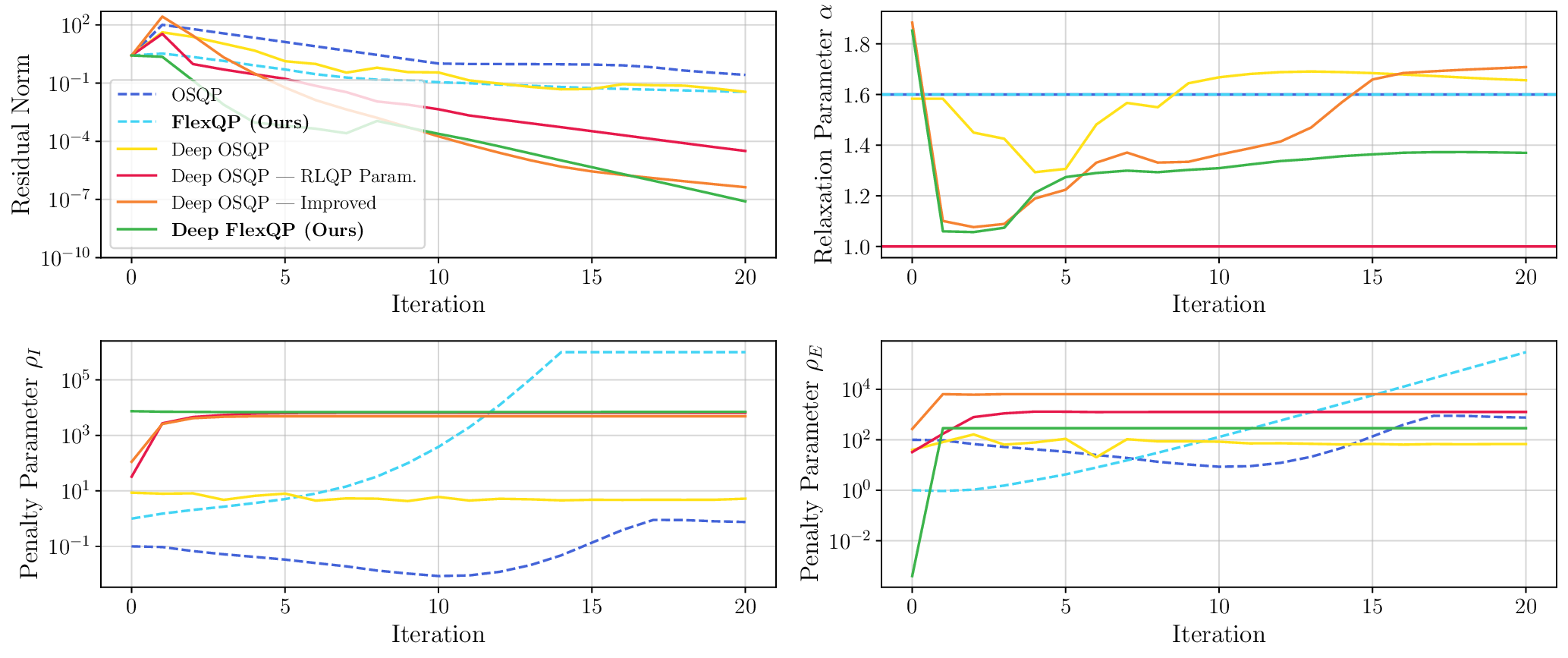
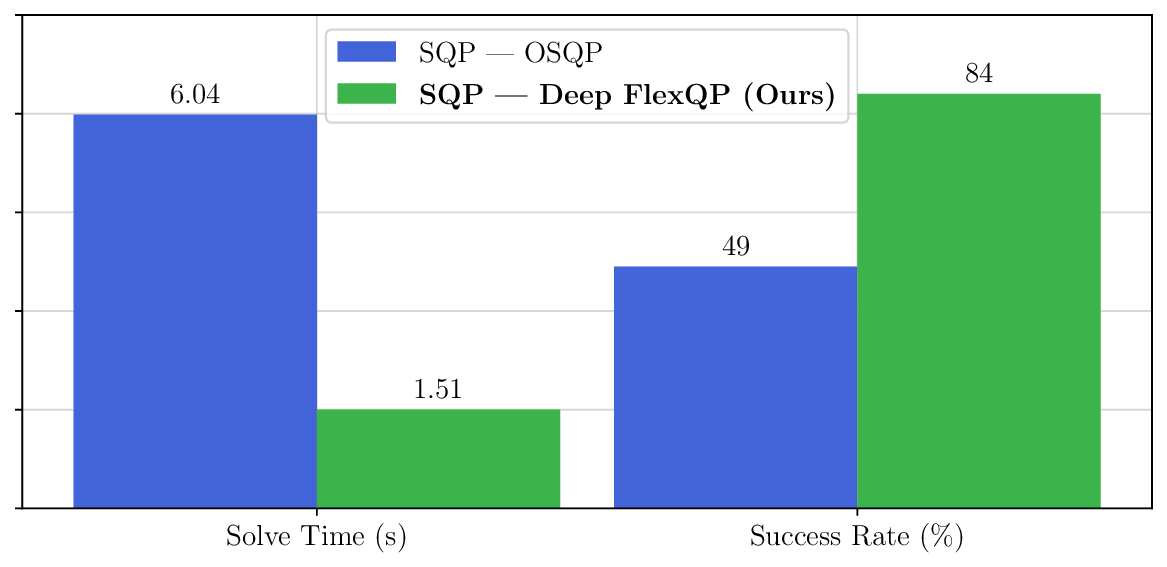
To this end, we propose FlexQP, a flexible QP solver that is always-feasible, meaning that it can solve any QP regardless of the feasibility of the constraints. Our method is based on an exact relaxation of the QP constraints: if the original QP was feasible, then FlexQP will identify the optimal solution. On the other hand, if the original QP was infeasible, instead of erroring or failing to return a solution, FlexQP automatically identifies the infeasibilities while simultaneously finding a point that minimizes the constraint violation. This allows FlexQP to be a robust QP solver in and of itself, but its power shines when used a submodule in an SQP-type method, see Figure 1. Moreover, through the relaxation of the constraints, multiple hyperparameters are introduced that can be difficult to tune and have a non-intuitive effect on the optimization. To address this shortcoming, we use deep unfolding (Monga et al., 2021) to design lightweight feedback policies for the parameters based on actual problem data and solutions for QP problems of interest, leading to an accelerated version titled Deep FlexQP. Learning the parameters in a data-driven fashion avoids the laborious process of tuning them by hand or designing heuristics for how they should be updated from one iteration to the next. Meanwhile, these data-driven rules have been shown to strongly outperform the hand-crafted ones, such as in the works by Ichnowski et al. (2021) and Saravanos et al. (2025).
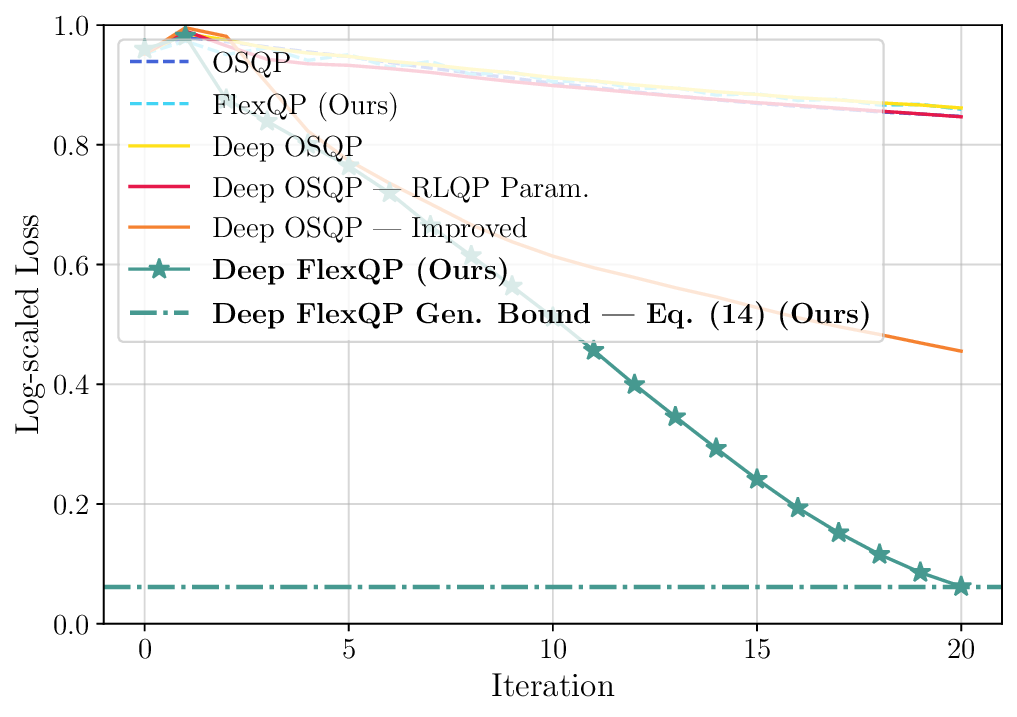
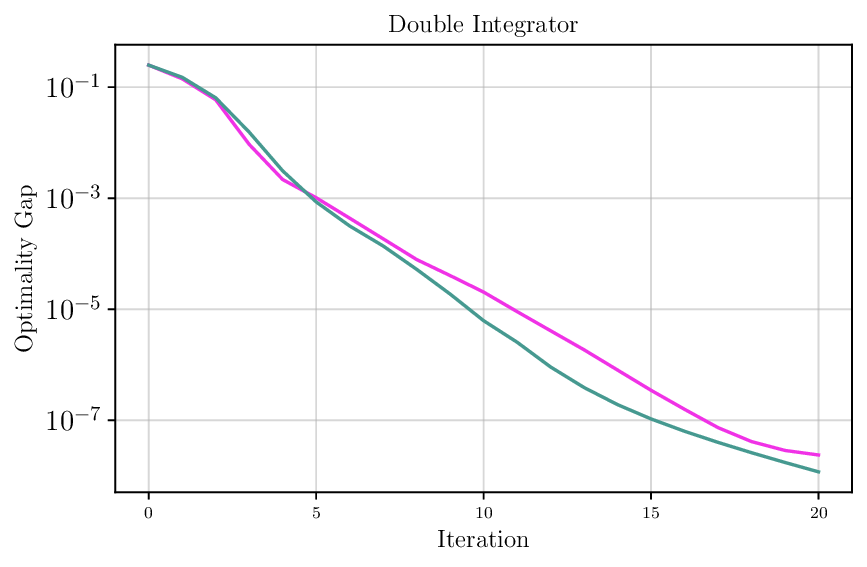
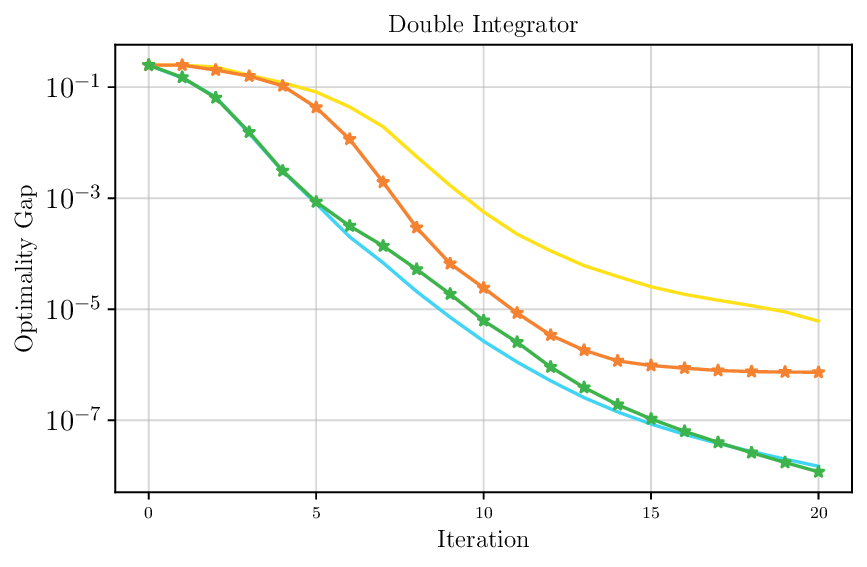
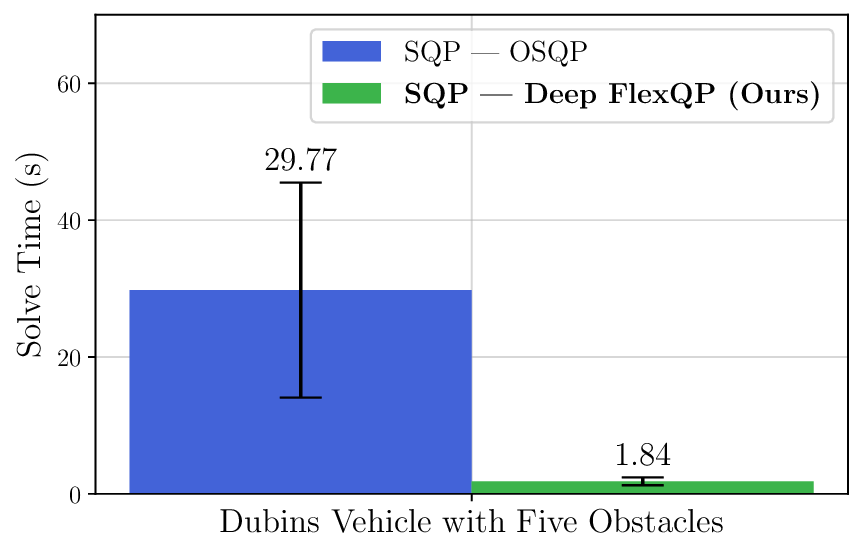
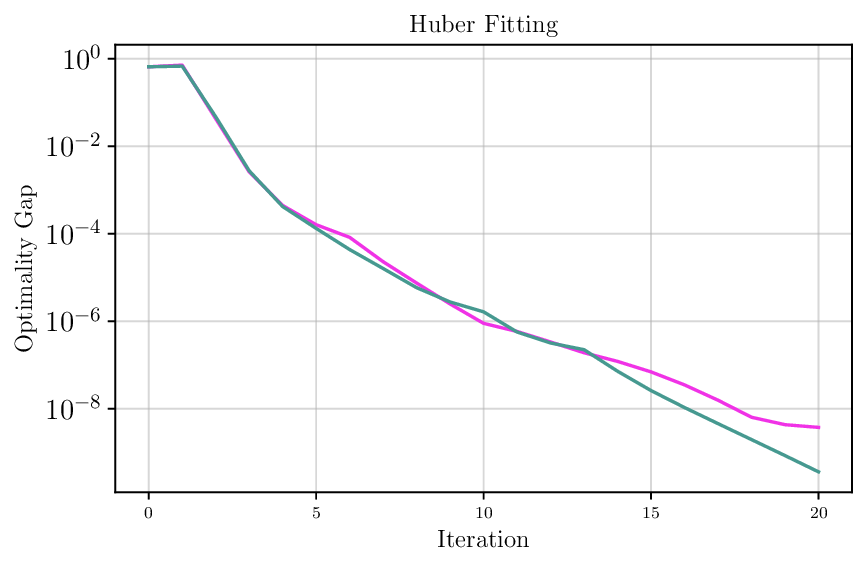
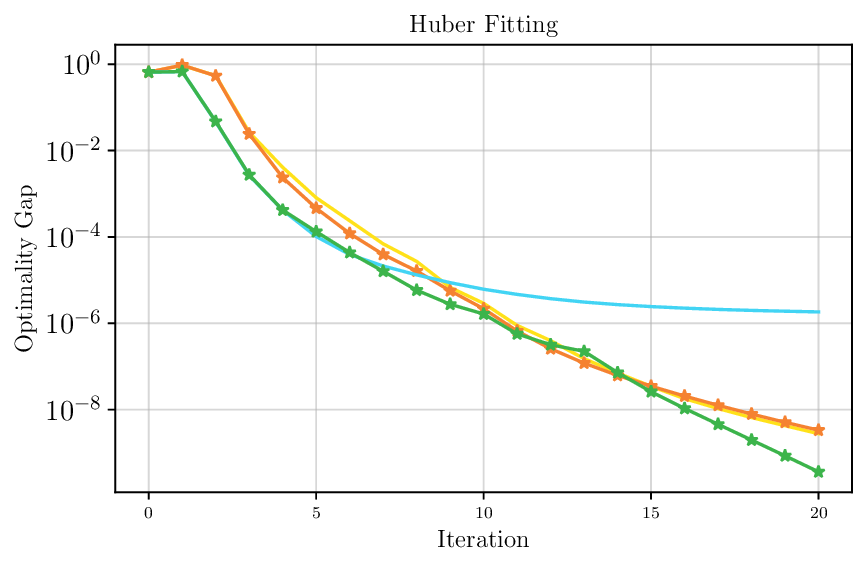
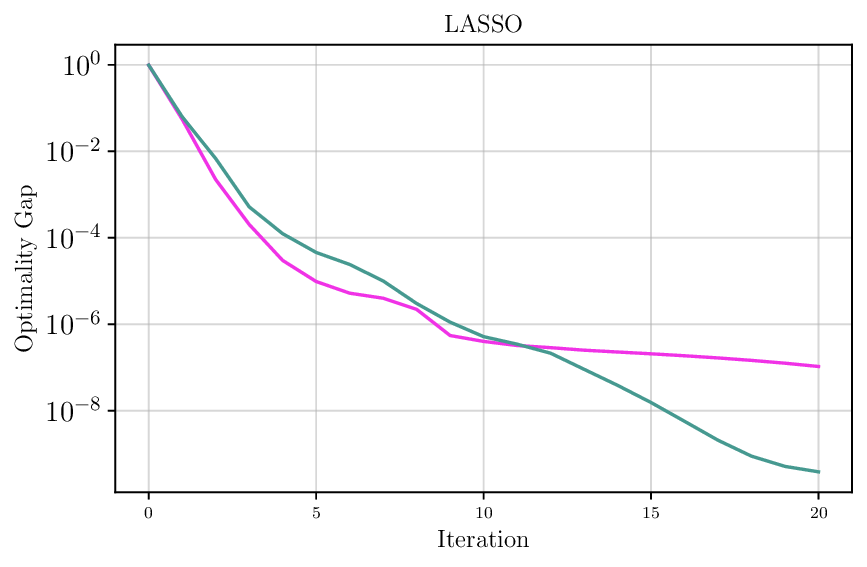
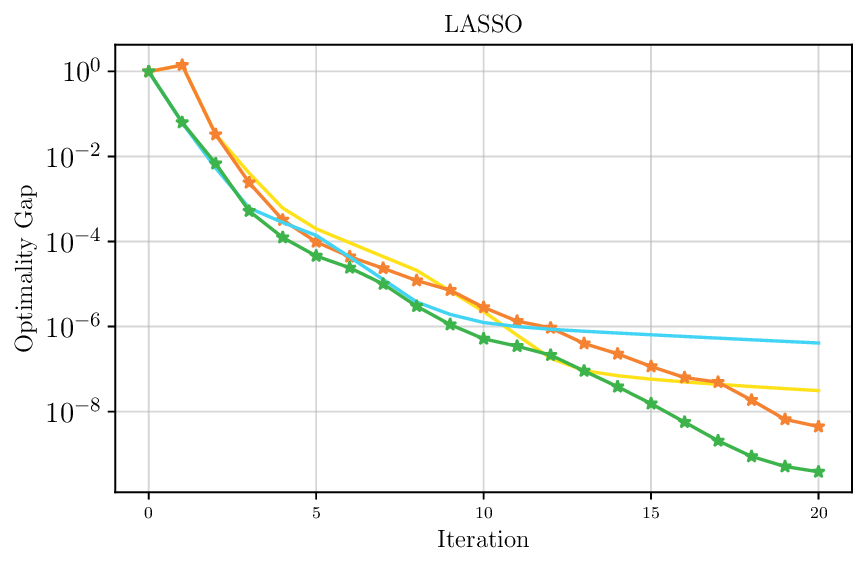
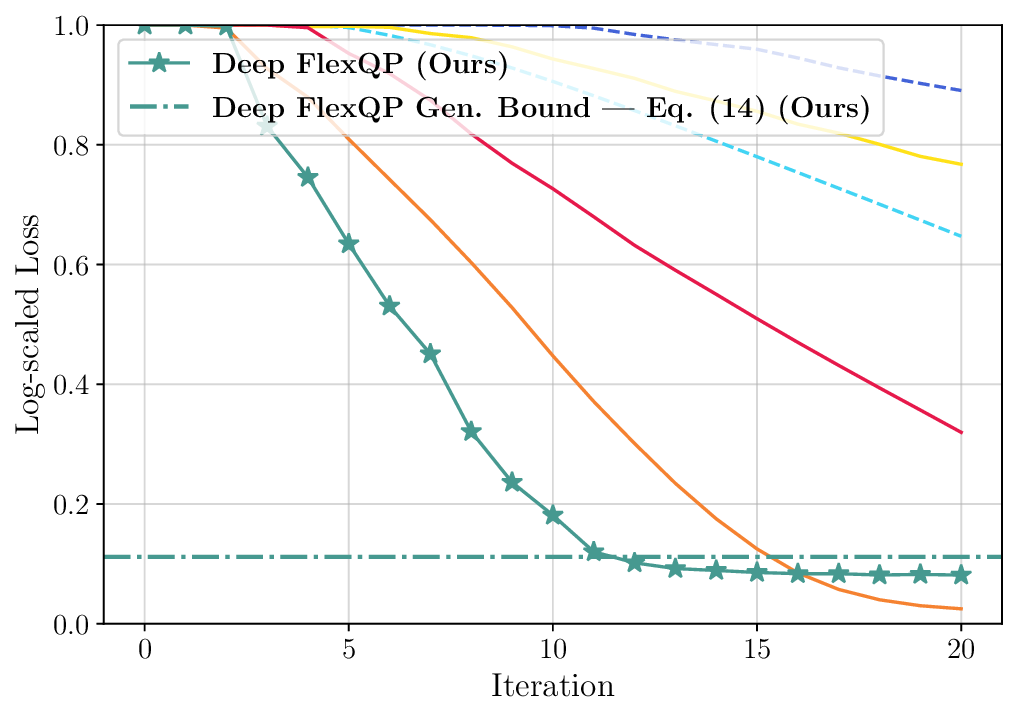
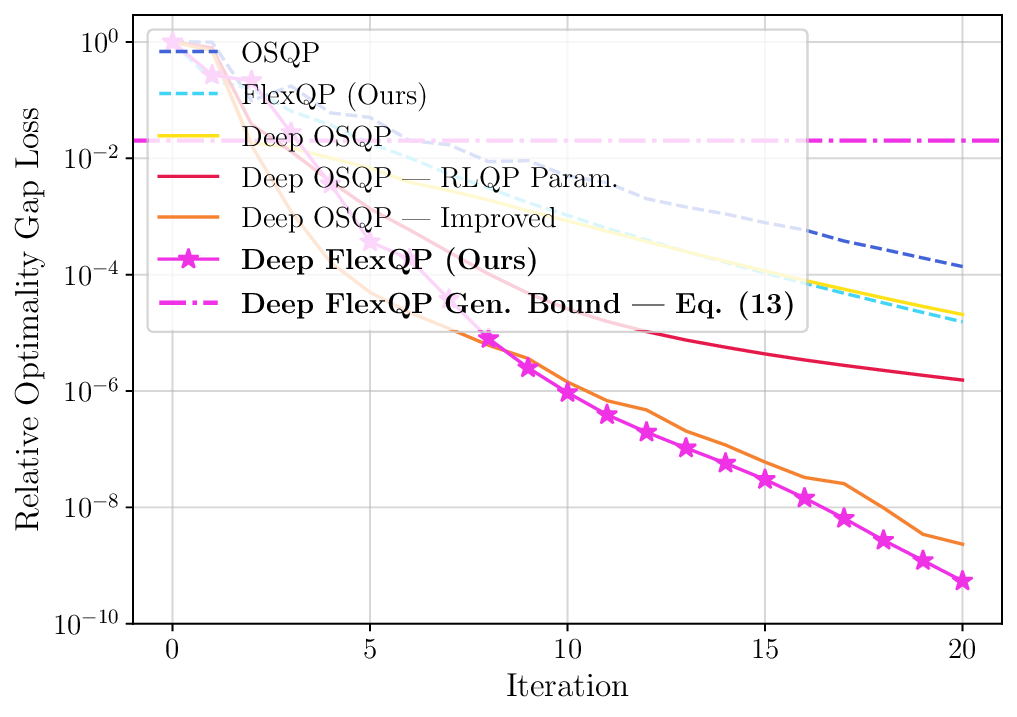
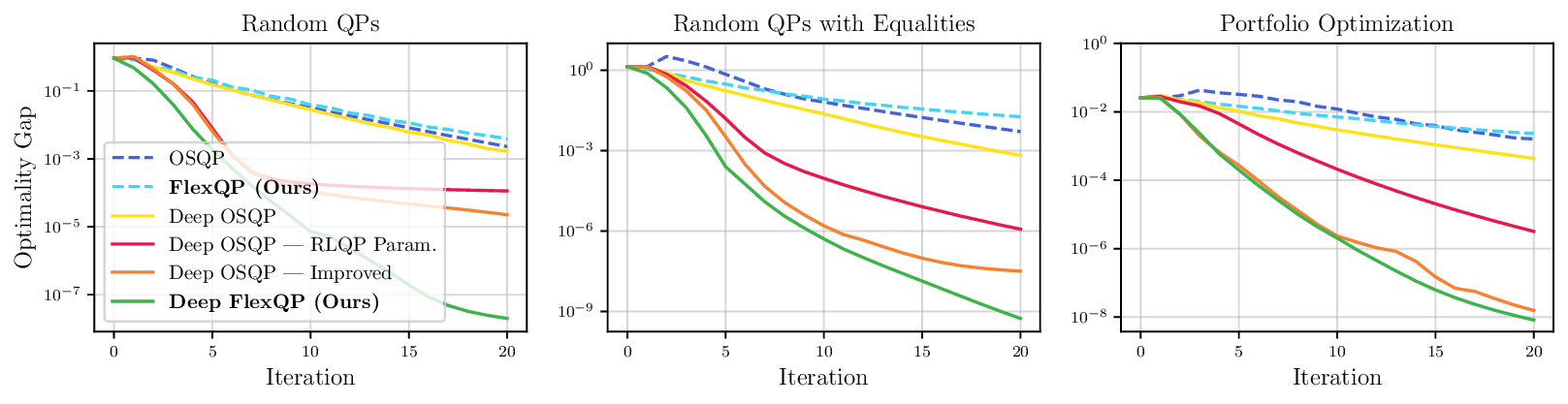
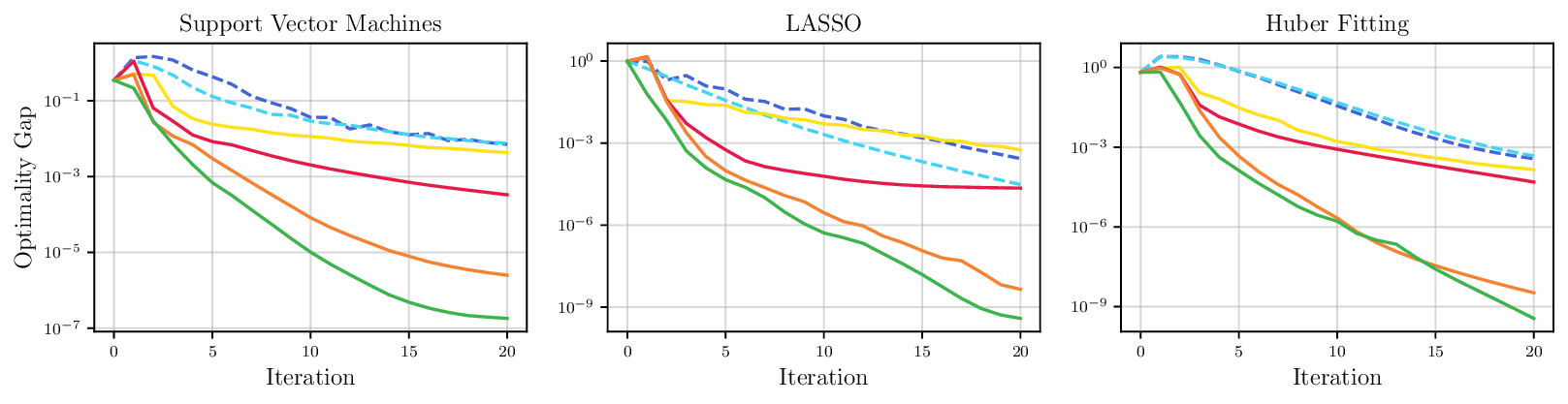
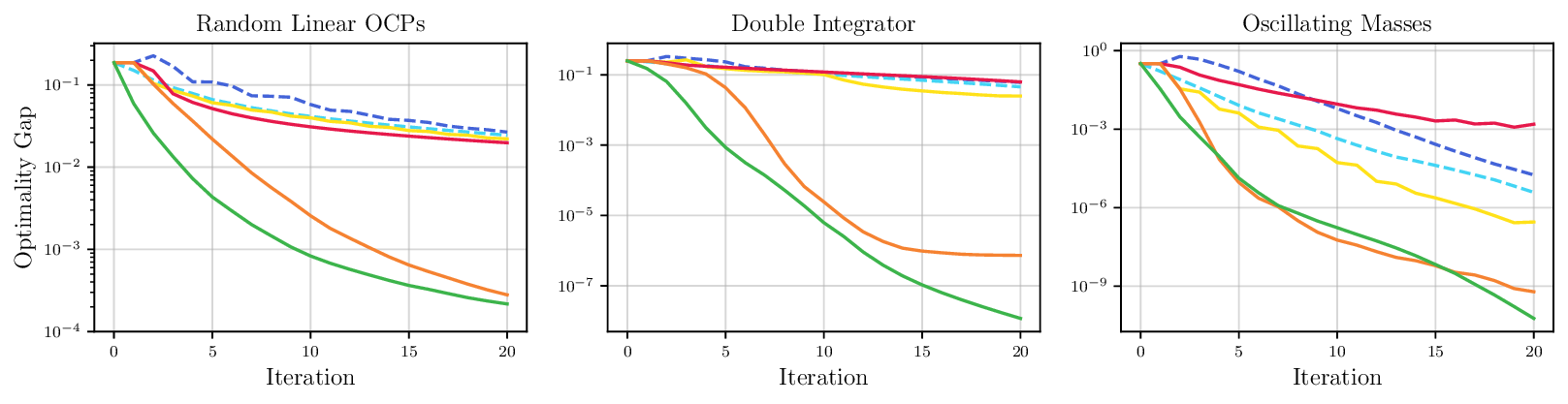
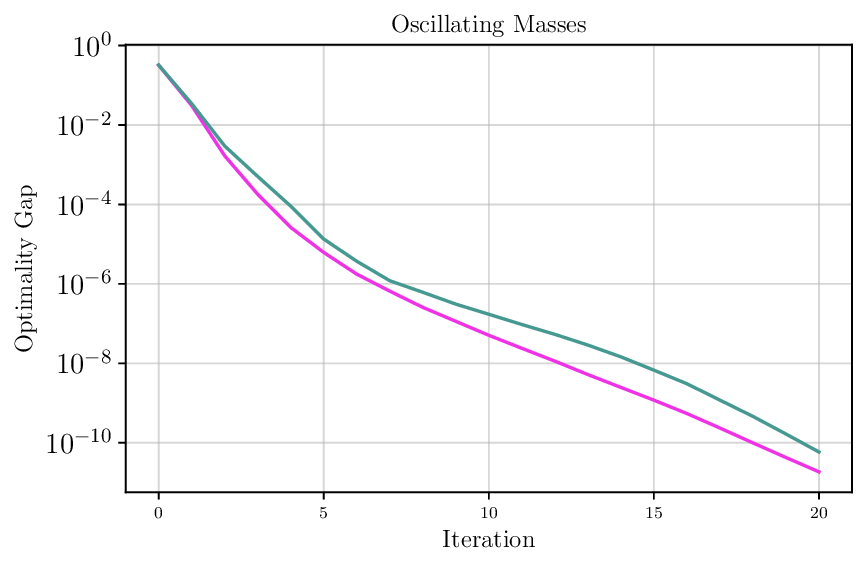
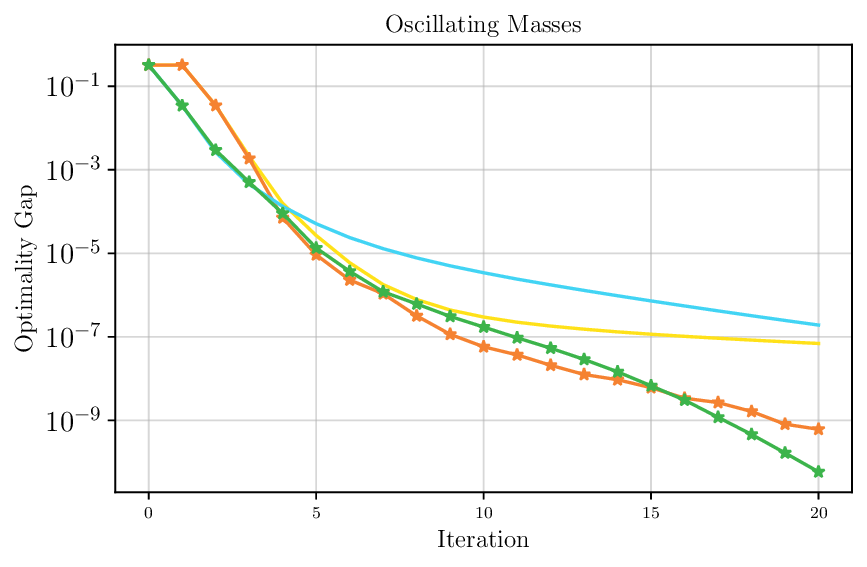
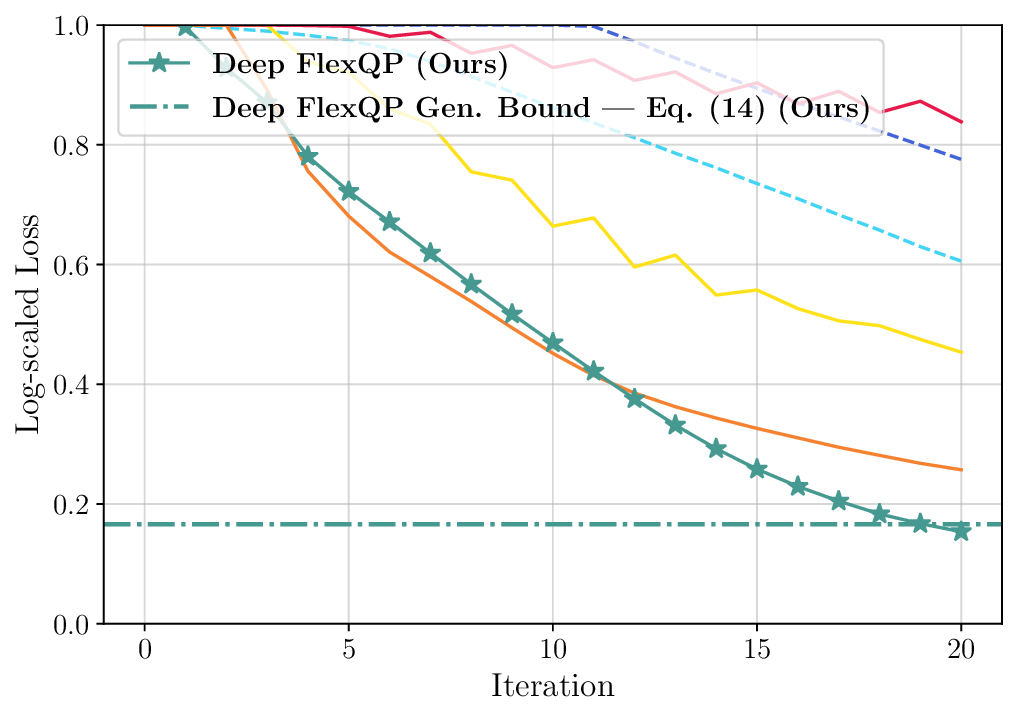
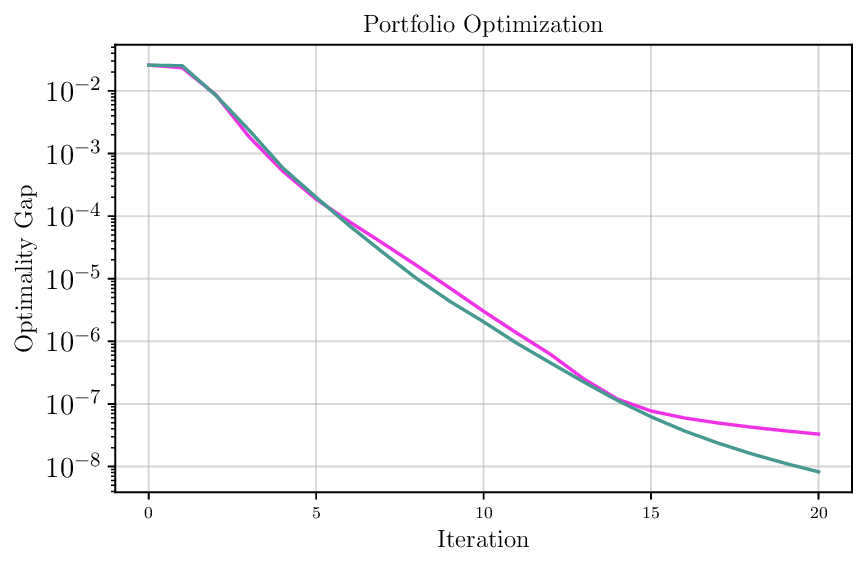
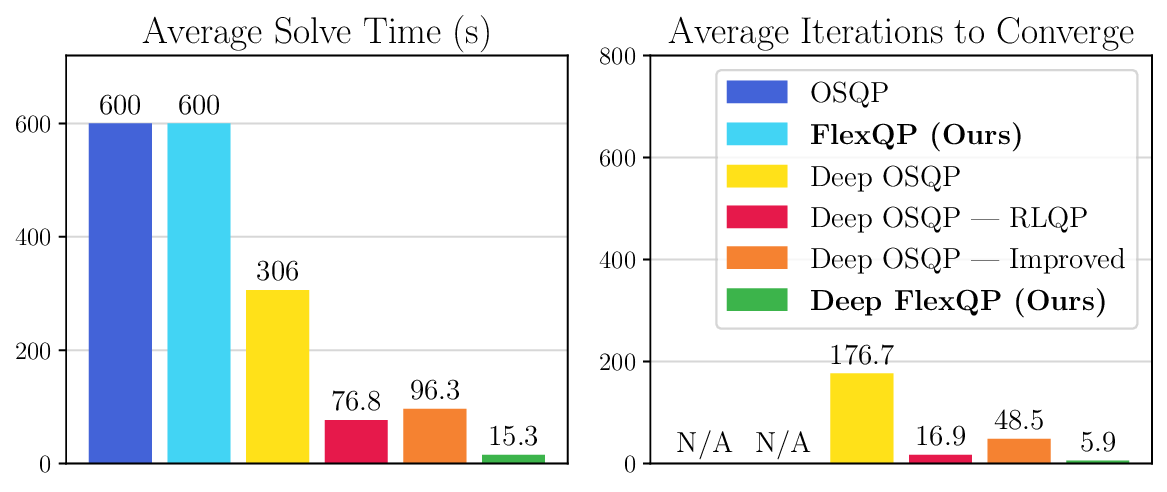
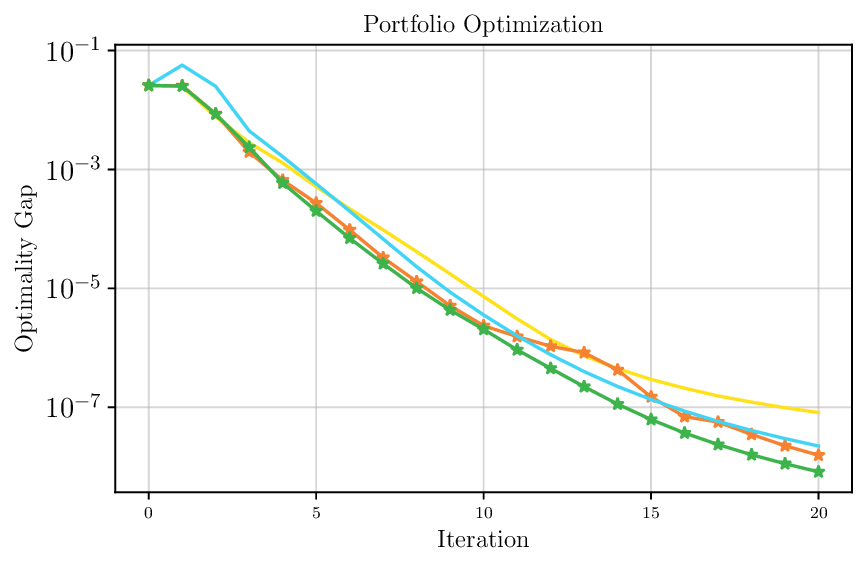
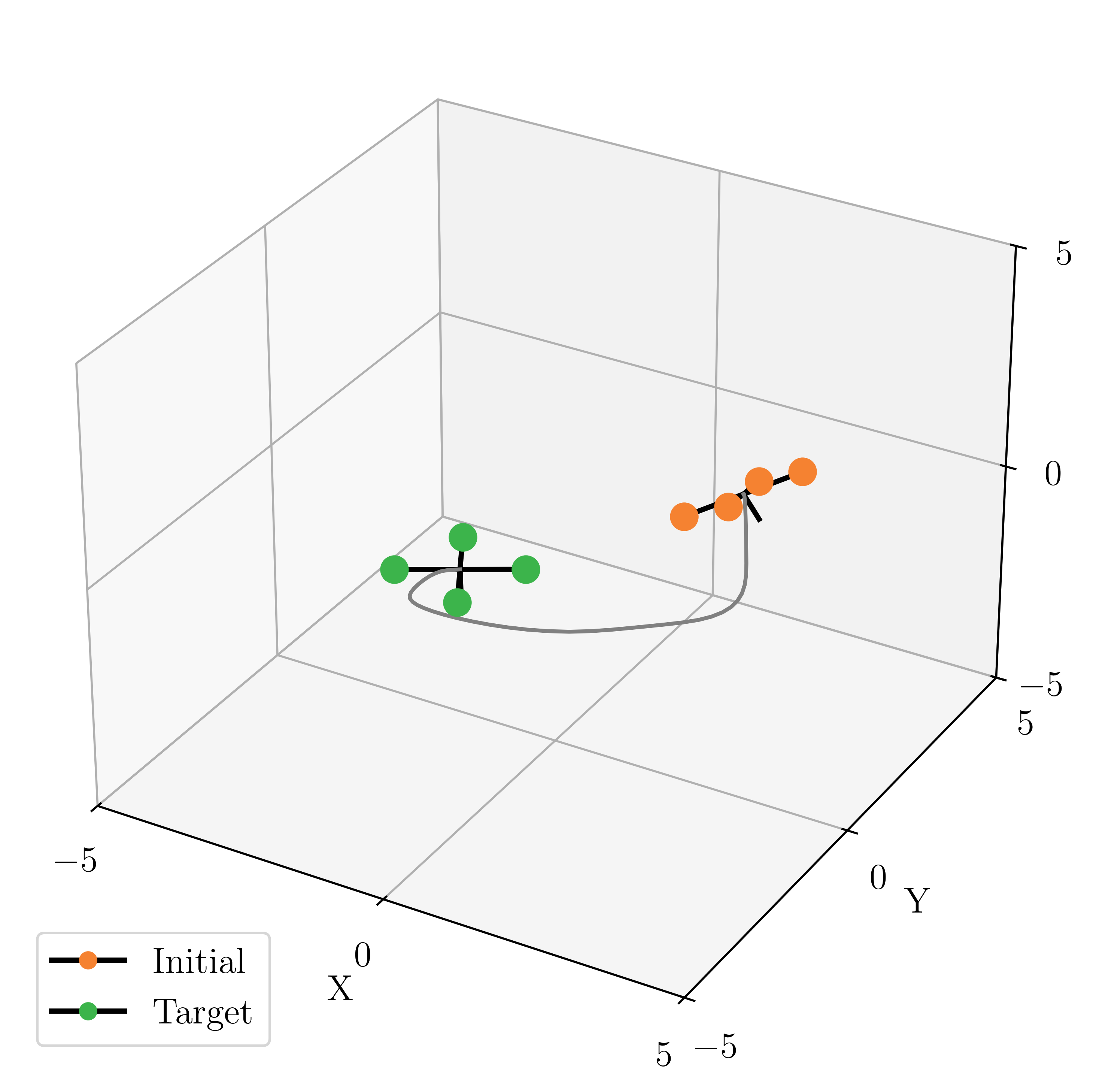
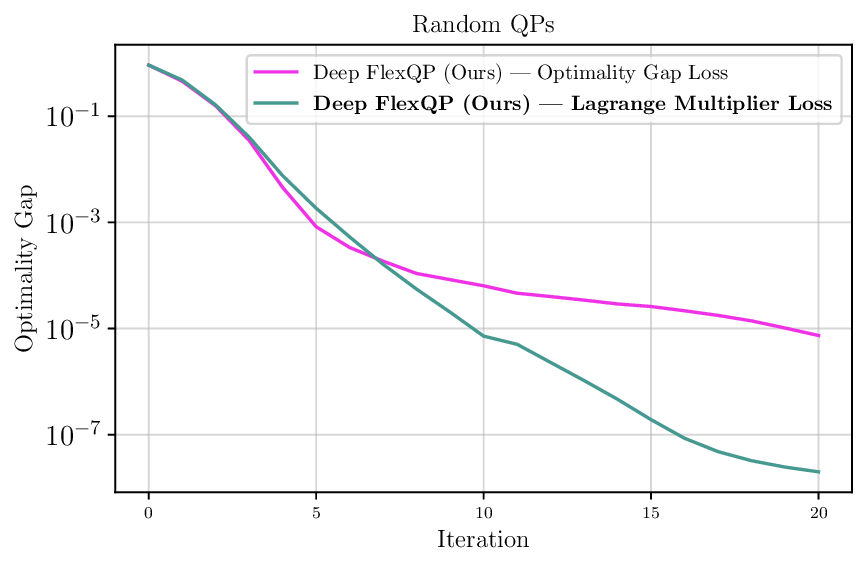
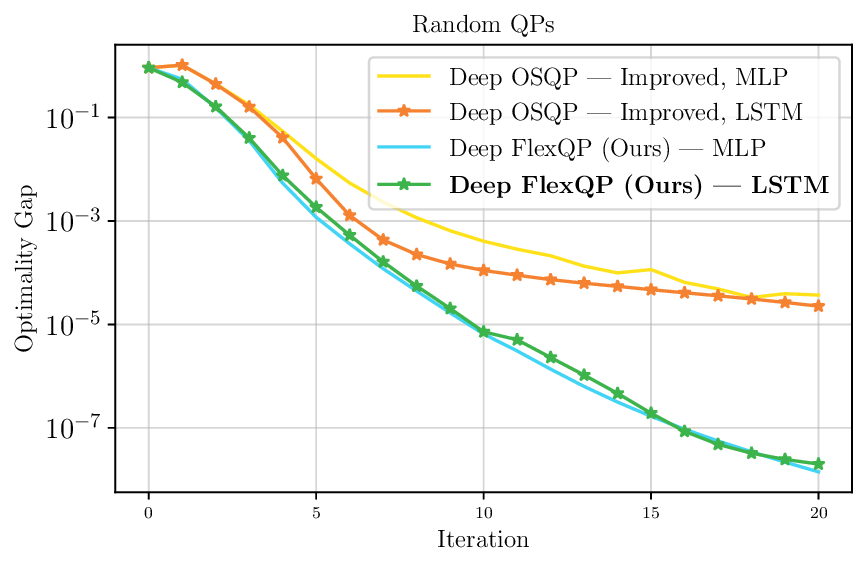
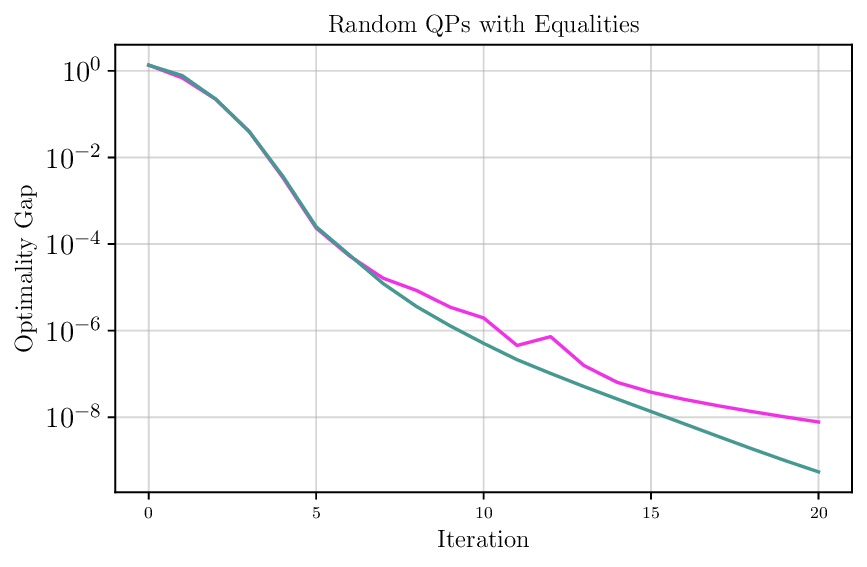
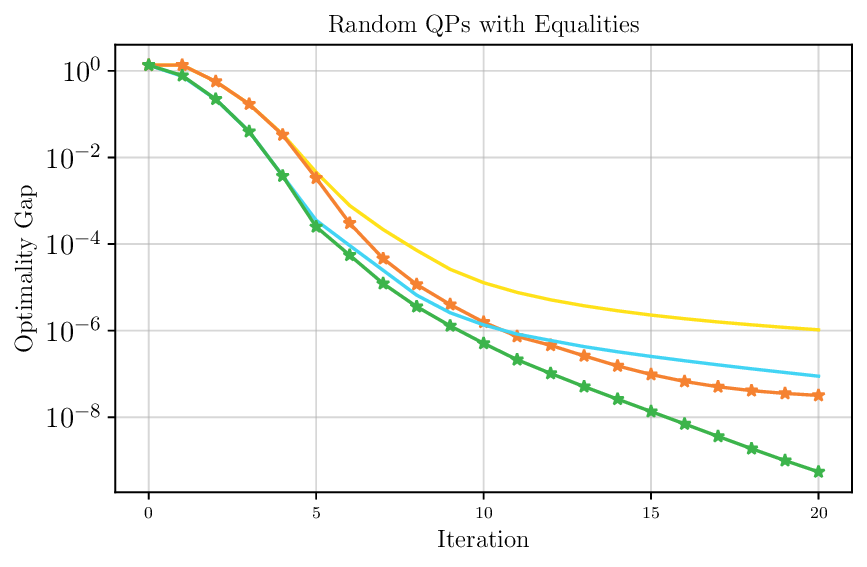
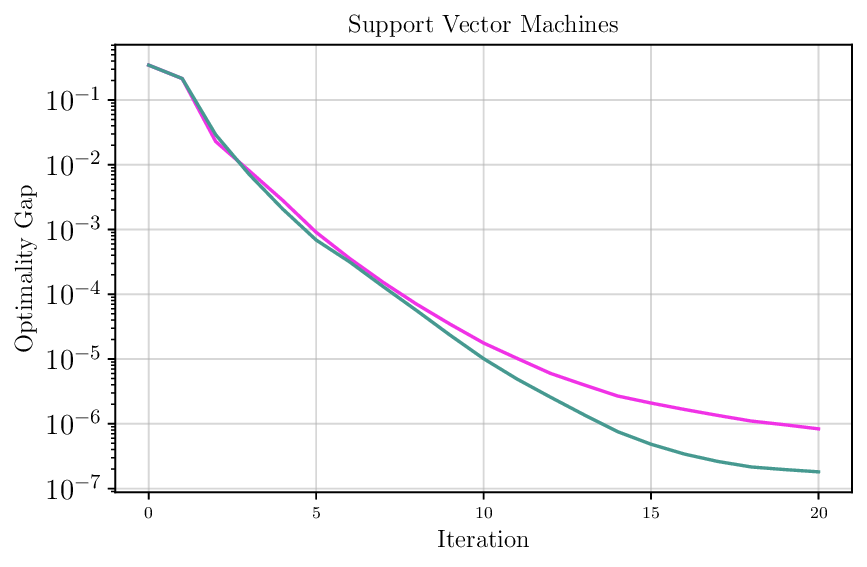
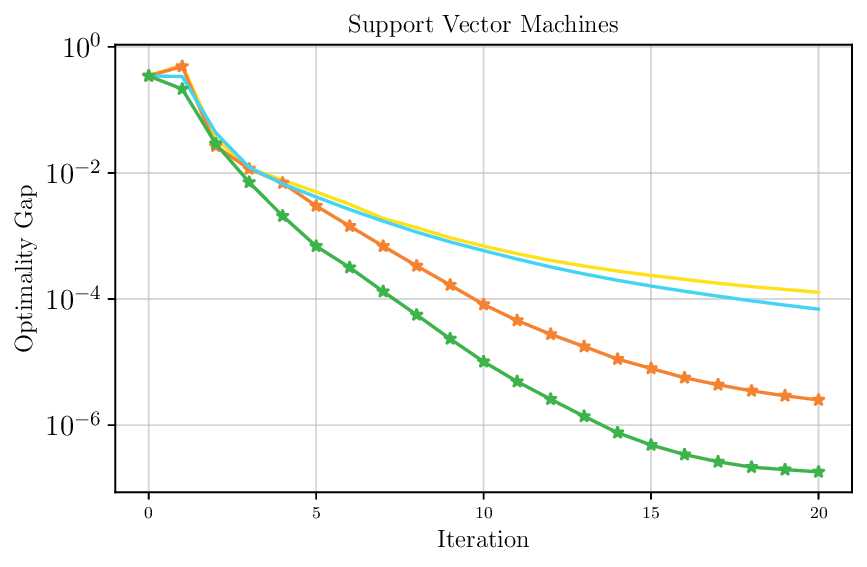
We thoroughly benchmark Deep FlexQP against traditional and learned QP optimizers on multiple QP problem classes including machine learning, portfolio optimization, and optimal control problems. Moreover, we certify the performance of Deep FlexQP through probably approximately correct (PAC) Bayes generalization bounds, which provide a guarantee on the mean performance of the optimizer. We propose a log-scaled training loss that better captures the performance of the optimizer when the residuals are very small. Finally, we deploy Deep FlexQP to solve nonlinearly-constrained trajectory optimization and predictive safety filter problems (Wabersich and Zeilinger, 2021). Overall, Deep FlexQP can produce an order-of-magnitude speedup over OSQP (Stellato et al., 2020) when deployed as a subroutine in an SQP-based approach (Figure 1), while also robustly handling infeasibilities that may occur due to a poor linearization or an over-constrained problem.
SQP solves smooth nonlinear optimization problems of the form minimize x f (x), subject to g(x) ≤ 0,
where f : R n → R twice-differentiable is the objective to be minimized and g : R n → R m and h : R n → R p differentiable describe the inequality and equality constraints, respectively. SQP solves Equation 1 by iteratively linearizing the constraints and quadraticizing the Lagrangian L(x, y I , y E ) := f (x) + y ⊤ I g(x) + y ⊤ E h(x) around the current iterate (x k , y k I , y k E ), where y I ∈ R m + and y E ∈ R p are the dual variables for the inequality and equality constraints, respectively. This results in the following QP subproblem:
subject to g(x k ) + ∂g(x k )dx ≤ 0, (2b)
Notably, the linearization of the constraints g and h may not produce a QP subproblem that is feasible, meaning that there may not
This content is AI-processed based on open access ArXiv data.