Multifractal analysis has revealed regularities in many self-seeding phenomena, yet its use in modern deep learning remains limited. Existing end-to-end multifractal methods rely on heavy pooling or strong feature-space decimation, which constrain tasks such as semantic segmentation. Motivated by these limitations, we introduce two inductive priors: Monofractal and Multifractal Recalibration. These methods leverage relationships between the probability mass of the exponents and the multifractal spectrum to form statistical descriptions of encoder embeddings, implemented as channel-attention functions in convolutional networks.
Using a U-Net-based framework, we show that multifractal recalibration yields substantial gains over a baseline equipped with other channel-attention mechanisms that also use higher-order statistics. Given the proven ability of multifractal analysis to capture pathological regularities, we validate our approach on three public medical-imaging datasets: ISIC18 (dermoscopy), Kvasir-SEG (endoscopy), and BUSI (ultrasound).
Our empirical analysis also provides insights into the behavior of these attention layers. We find that excitation responses do not become increasingly specialized with encoder depth in U-Net architectures due to skip connections, and that their effectiveness may relate to global statistics of instance variability.
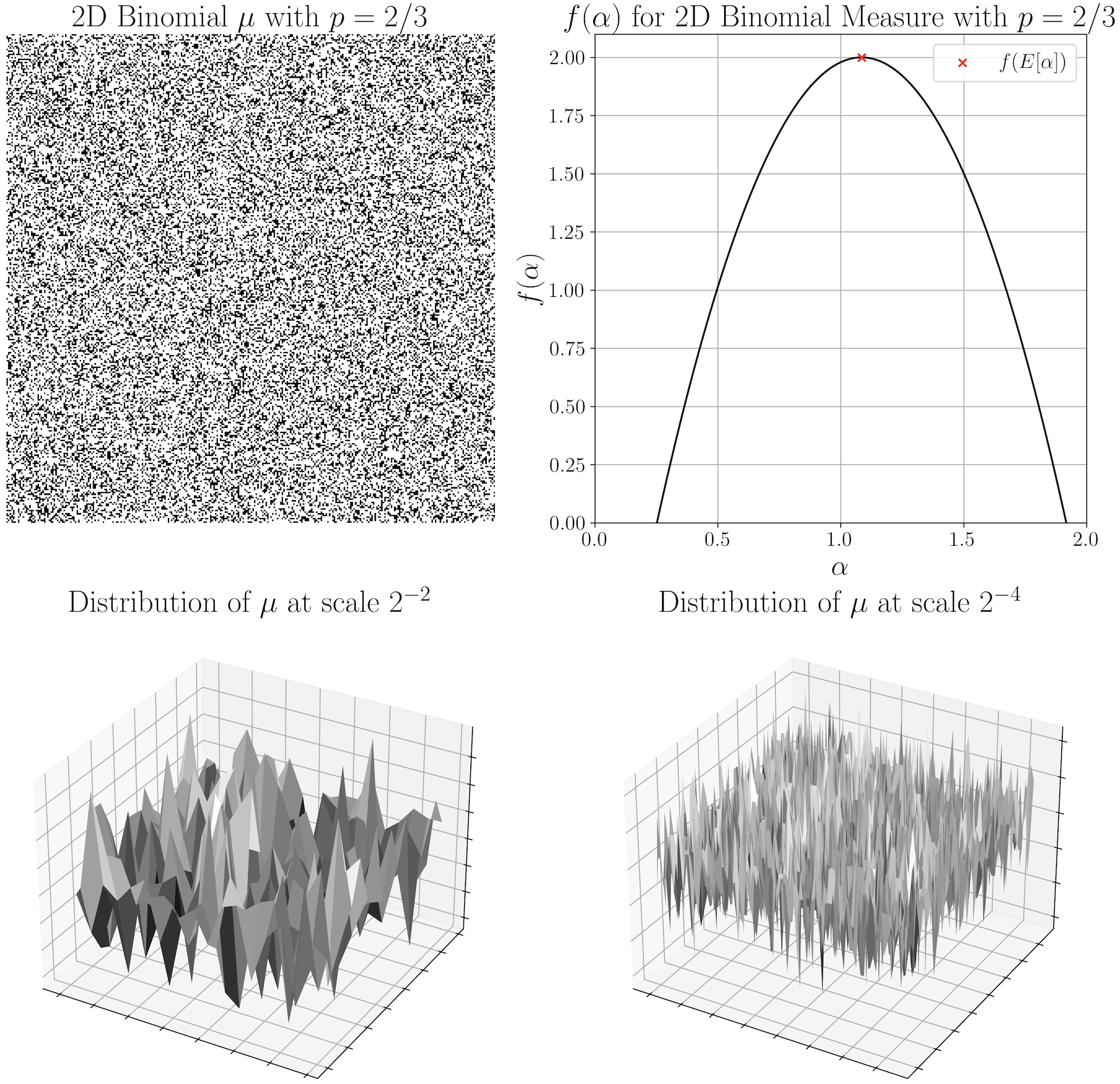
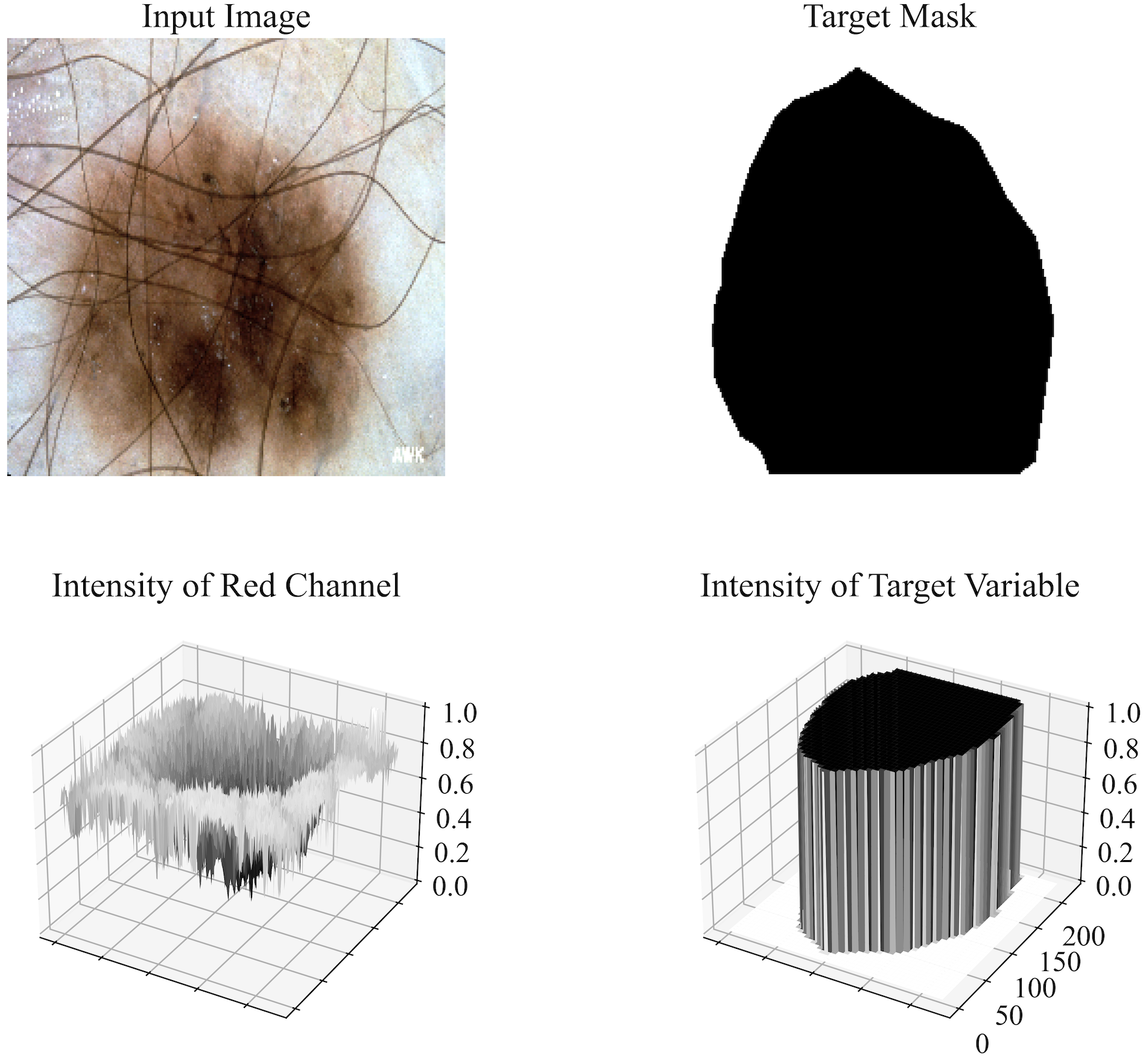
Pathological phenomena may be described as a state of a physiological system that evolves in a self-seeding, cascading fashion [33]. These states are observed as complex patterns in medical imaging modalities, whose regularities may be disentangled through the lens of Fractal Geometry, the field of mathematics centered around the study of mathematical structures that have finestructure, i.e., detail at all scales [15]. This degree of scale-invariance may be captured in terms of a single (monofractal) or multiple (multifractal) scaling exponents that embody the dimension of the structure [14]. This self-similarity in distribution across scale is especially useful to describe textures as stationary stochastic processes [9,69,72,11].
In Medical Imaging, both structural and surface-level regularities may be leveraged [33]. Examples range from histology [3,46,56], endoscopy [19,49], dermoscopy [52,8], to magnetic resonance imaging (MRI) [35,28,37] and many others (see [39,33] and references therein). On the other hand, Fractal Geometry has received limited attention in the deep learning era, especially in the design of end-to-end architectures. This trend recently changed, and some successful approaches have been proposed for texture classification [72,11,10] and few-shot learning [76]. Bridging this gap for semantic segmentation is the main contribution of this paper, under the assumption that the inductive prior of a convolutional neural network (CNN) encoder carries information about the image’s scaling laws across its layers.
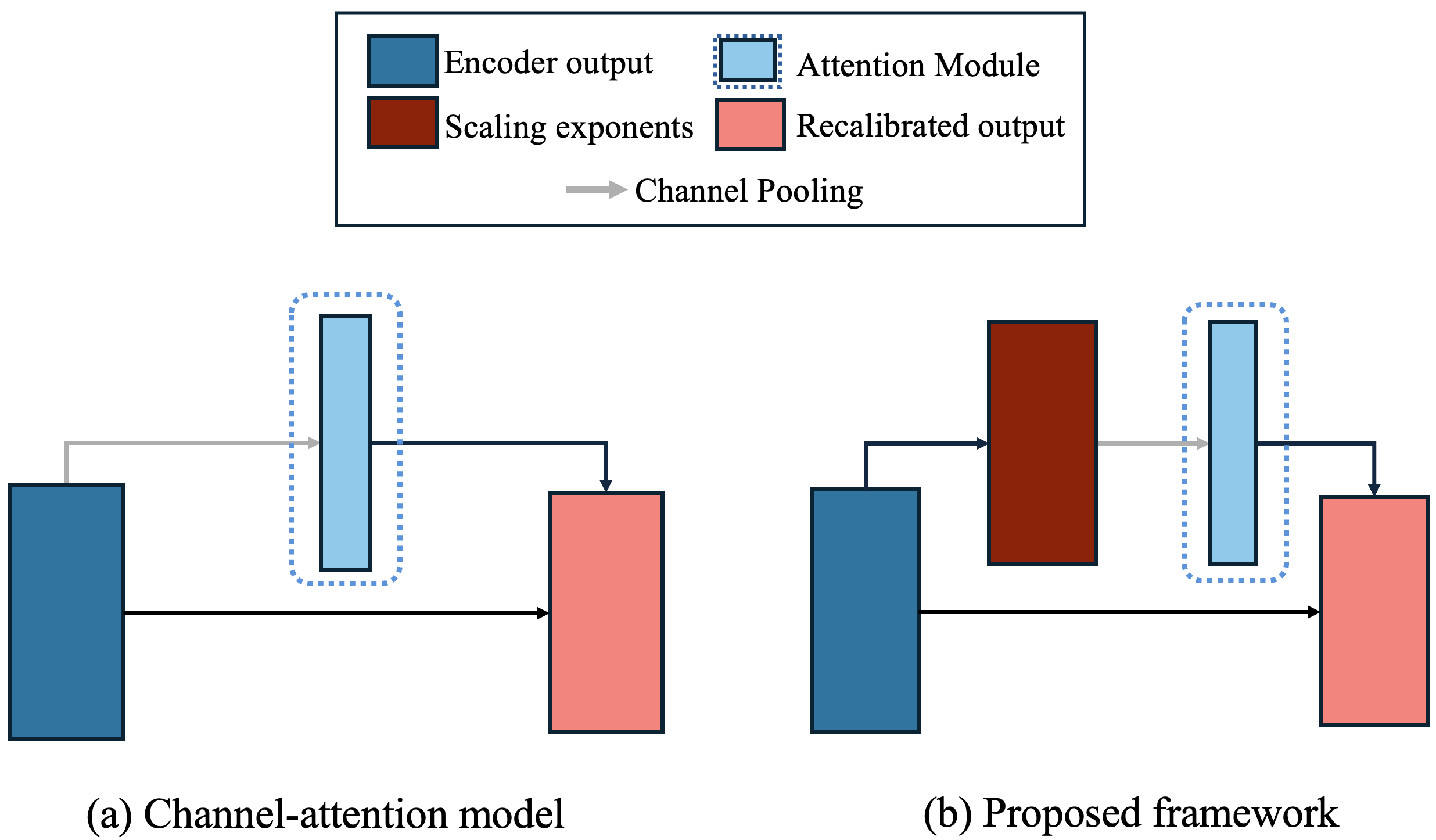
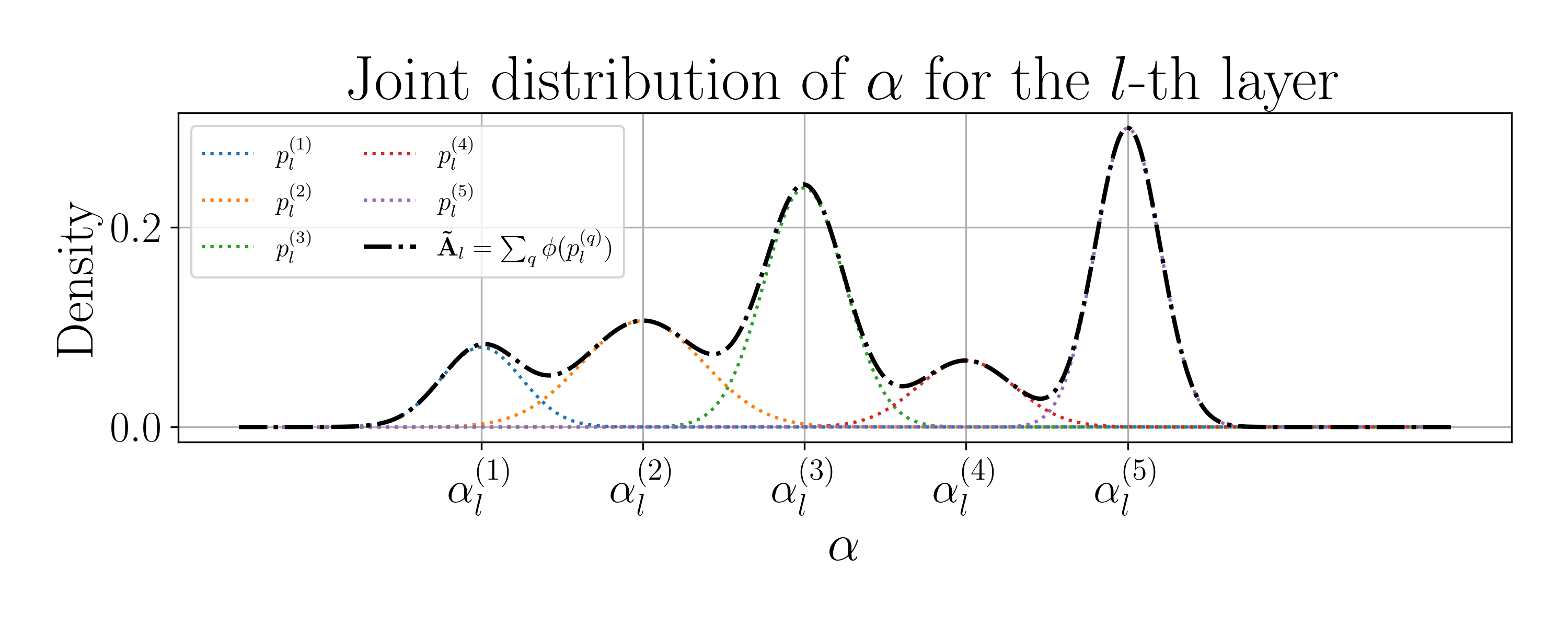
Grounded in multifractal analysis, we propose two new attention functions designed around the U-Net [57] , the main specialist model alternative to current foundational approaches [26,27,42]. These functions describe cross-channel dynamics by deriving single or multiple statistics over the local scaling exponents of each filter (see Figure 1). We show substantial improvements over several attention functions [58,38,53] in terms of segmentation performance in three public medical image segmentation datasets. During this investigation we also conduct an empirical analysis in an effort to shed some light on the reason behind the disparity of performance between different statistical channel functions. Our findings suggest that intuitions held by the community behind the mechanisms that govern these layers [22,58,51,18] do not seem to hold in the case of semantic segmentation. Briefly, our experiments suggest that these functions do not seem to learn to “filter non-informative channels”. Inspection of their response dynamics are indeed antithetical to this assumption: a certain range of instance variability is actually desirable.
Current end-to-end architectures [72,11,10] that leverage multifractal primitives (described in Section 2.3) are engineered for recognition, and most draw parallels with the underlying formalism in a very ad hoc fashion. We only identified the fractal encoder in [72] to be close to a true multifractal prior. Moreover, these methods rely on computationally expensive fusion approaches that require spatial or channel upsampling and/or downsampling [72,76,10], aggressive shape normalization across spatial and channel dimensions [11], and inefficient [10] or repeated computations [11] of extensions of the differential box counting (DBC) algorithm.
We address these issues by deriving statistics over the local scaling exponents with a theoretically guided rationale. This work has a special focus on the U-Net, but note that the methods set forth may be readily applied to any deep neural network (DNN) architecture. We then draw inspiration from statistical channel attention functions [22,58,38,53,18], but we recalibrate the output of the network as a function of the scaling exponents, instead of using the direct responses of each encoder block.
This paper also extends very preliminary empirical work where we presented an early version of Monofractal recalibration [43]. However, the experimental setup has been substantially upgraded with more extensive and rigorous statistical analyses, more datasets, better training and crossvalidation routines, more baseline architectures [58,38,53] and ablation experiments, and a more detailed analysis of how these attention mechanisms behave. Finally, we propose an entire new attention module that displays superior performance in general: Multifractal recalibration. All of the introduced inductive priors are also studied from a principled perspective through the lens of multifractal anaylsis.
Our main contributions are summarized as follows1 :
An efficient end-to-end way to compute the local scaling exponents adequate for dense prediction tasks.
Two novel attention functions thoeretically grounded in multifractal analysis.
An experimental analysis of other statistically informed recalibration strategies beyond squeezeand-excitation (SE) [58], such as style based recalibration (SRM) [38] and frequency channel attention (
This content is AI-processed based on open access ArXiv data.