Topologically ordered states are among the most interesting quantum phases of matter that host emergent quasi-particles having fractional charge and obeying fractional quantum statistics. Theoretical study of such states is however challenging owing to their strong-coupling nature that prevents conventional mean-field treatment. Here, we demonstrate that an attention-based deep neural network provides an expressive variational wavefunction that discovers fractional Chern insulator ground states purely through energy minimization without prior knowledge and achieves remarkable accuracy. We introduce an efficient method to extract ground state topological degeneracy -- a hallmark of topological order -- from a single optimized real-space wavefunction in translation-invariant systems by decomposing it into different many-body momentum sectors. Our results establish neural network variational Monte Carlo as a versatile tool for discovering strongly correlated topological phases.
Introduction -The recent discovery of the fractional quantum anomalous Hall effect [1][2][3][4][5] opened an exciting frontier for studying fractional topological phases in quantum materials characterized by the emergence of fractional charge and fractional statistics. In both twisted MoTe 2 and rhombohedral graphene moiré systems, the observed fractional quantum anomalous Hall states feature a series of quantized Hall conductance plateaus in the absence of an external magnetic field, which exactly match those of fractional quantum Hall states in two-dimensional electron systems under strong magnetic fields. This striking correspondence can be understood from topological order [6]-a unified description of fractionally quantized Hall conductance, fractional charge, and fractional quantum statistics.
Historically, topological order has long played a key role in the study of fractional Hall states in Landau levels and Chern bands. As a matter of fact, prior to the recent experimental breakthrough, fractional quantum anomalous Hall states-or zero-field fractional Chern insulators [7][8][9][10] -were theoretically predicted in twisted bilayer graphene [11][12][13] and twisted transition metal dichalcogenides (TMDs) [14,15] based on the numerical diagnosis of topological orders. On the theory side, most computational studies have primarily relied on exact diagonalization (ED) and the density-matrix renormalization group (DMRG). In ED, topological order is typically diagnosed through ground-state degeneracy on the torus, the manybody Chern number, or entanglement spectroscopy.
While both methods have been rather successful, they suffer from notable drawbacks. ED, though unbiased, is limited to small system sizes and often restricted to few energy bands due to the exponential growth of the Hilbert space, and therefore cannot capture strong bandmixing effects [16,17]. On the other hand, DMRG can treat larger systems but is essentially a quasi-onedimensional method, making it difficult to apply to strictly two-dimensional geometries.
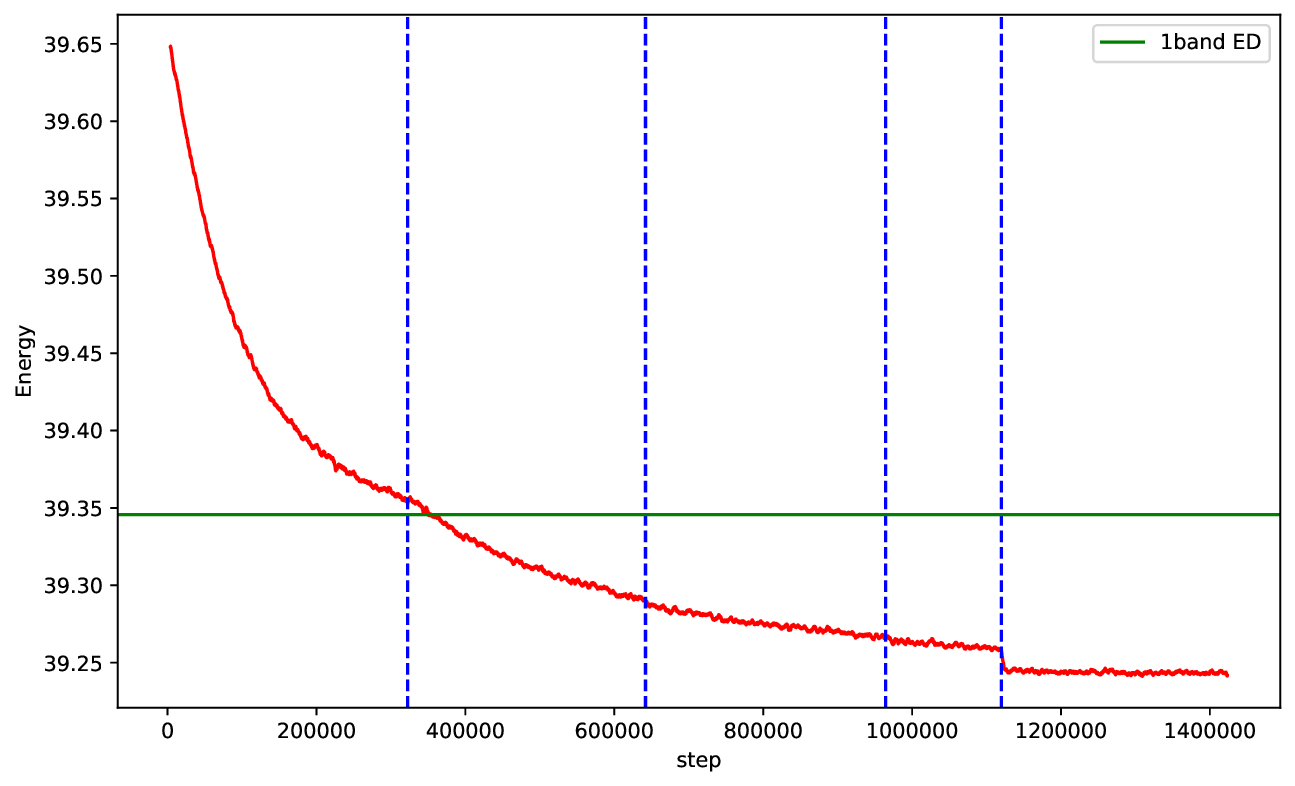
Recently, neural network variational Monte Carlo (NN-VMC) [18] has emerged as a promising numerical method for strongly interacting systems which is able to overcome these drawbacks. First, VMC can be directly formulated in terms of first-quantized wavefunctions making it wellsuited for studying various systems such as moiré materials which are described by continuum models.
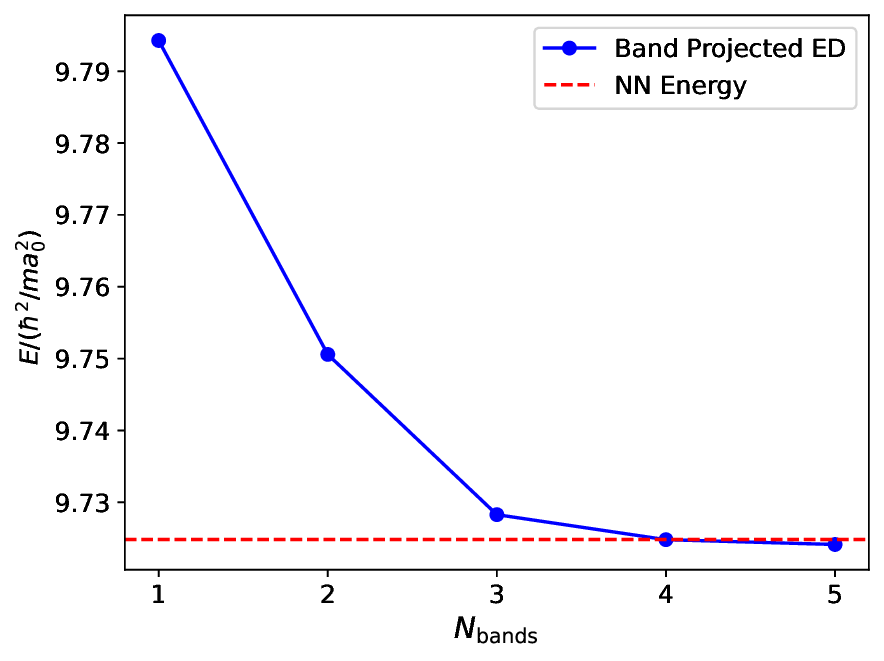
Second, the computational complexity of VMC scales polynomially with the number of particles [19], implying that simulations can, in principle, be pushed to larger systems. In addition, the expressivity of neural networks enables a variational ansatz capable of describing highly nontrivial quantum phases, including topological order and chiral superconductivity [20,21]. Importantly, as NN-VMC is carried out directly in real space, it accounts for all energy bands without truncation, thereby capturing arbitrary band-mixing effects. Moreover, it readily adapts to various two-dimensional geometries.
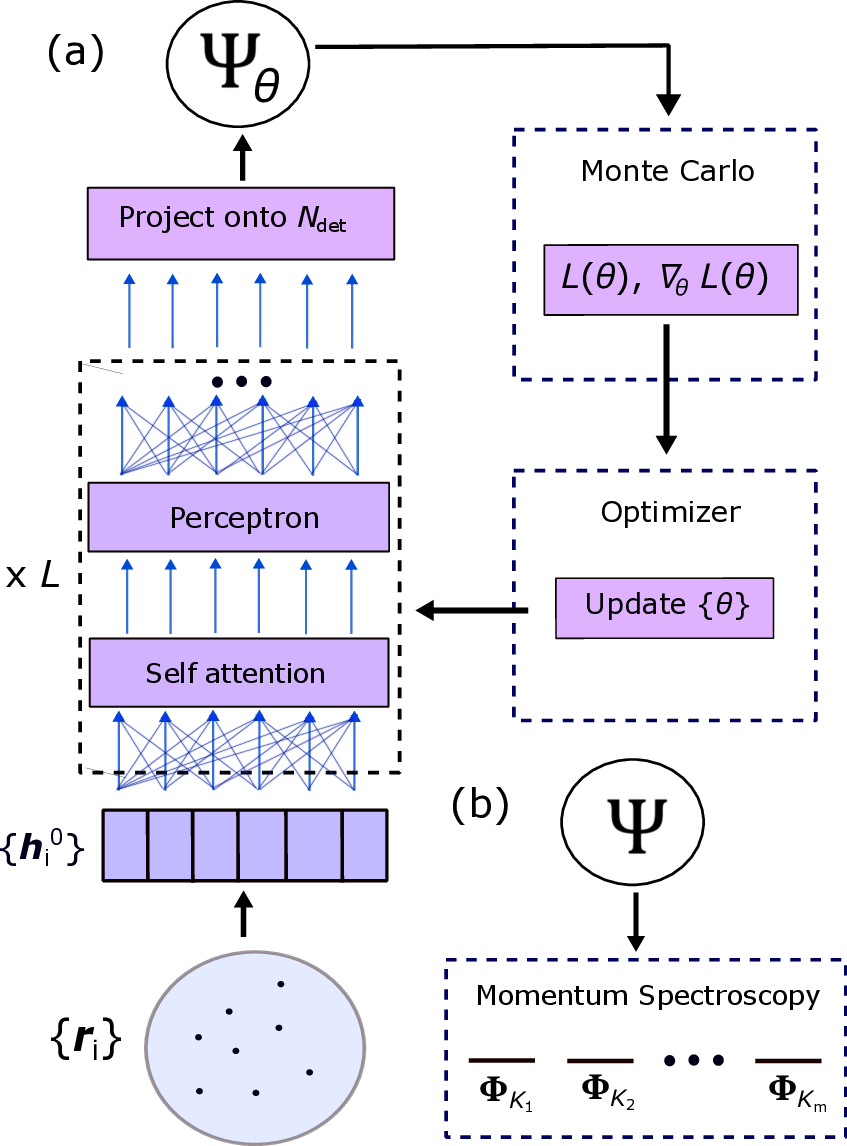
However, the application of VMC to topological order has been challenging. In the VMC method, a trial many-body wavefunction Ψ {θ} ({r i }) is optimized to minimize the ground state energy which raises a natural question, how to detect topological order from a single variational ansatz Ψ {θ} ({r i }) ? As topological order is highly non-local, it is impossible to be diagnosed with any local observable. On one hand, topological order can be generally detected from a single wavefunction by extracting the topological part of entanglement entropy [22,23]. However, the approach has been proven to be quite delicate, requiring careful subtraction of area-law contributions and the application of certain tricks to efficiently sample the reduced density matrix [24][25][26][27]. It is not clear a priori if there are efficient ways to diagnose topological order in variational wavefunctions that possess a large number of parameters, e.g., weights and biases in neural wavefunctions.
A hallmark of topological order is ground state degeneracy on closed-surface manifolds with non-zero genus g ̸ = 0 [28,29]. Unlike symmetry breaking states, topologically degenerate ground states are locally indistinguishable and only differ from each other in nonlocal observables. The existence of topological degeneracy is di-rectly related to the existence of fractional quasiparticles, or anyons. In particular, topological degeneracy on the torus (g = 1) equals the number of anyon types.
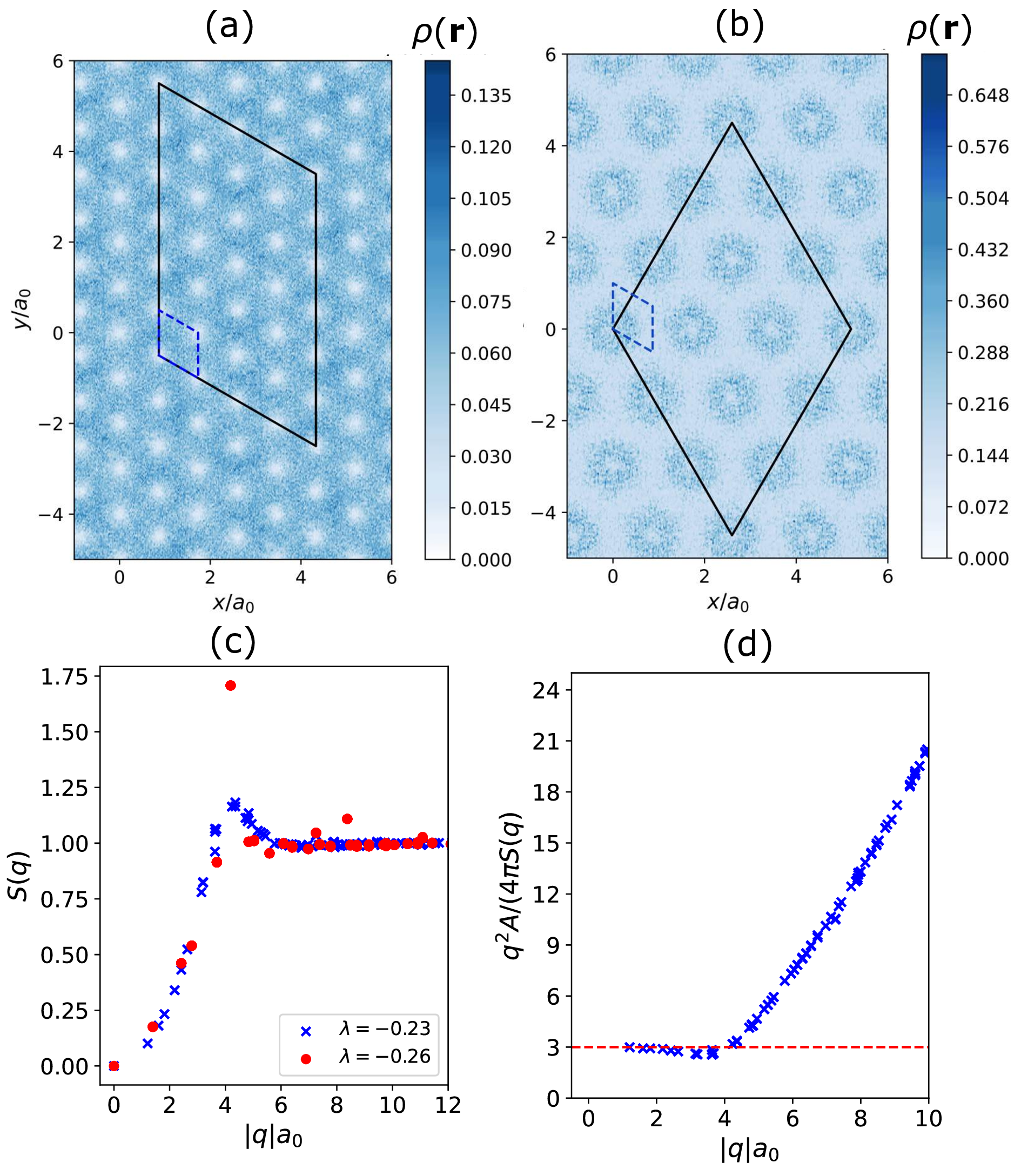
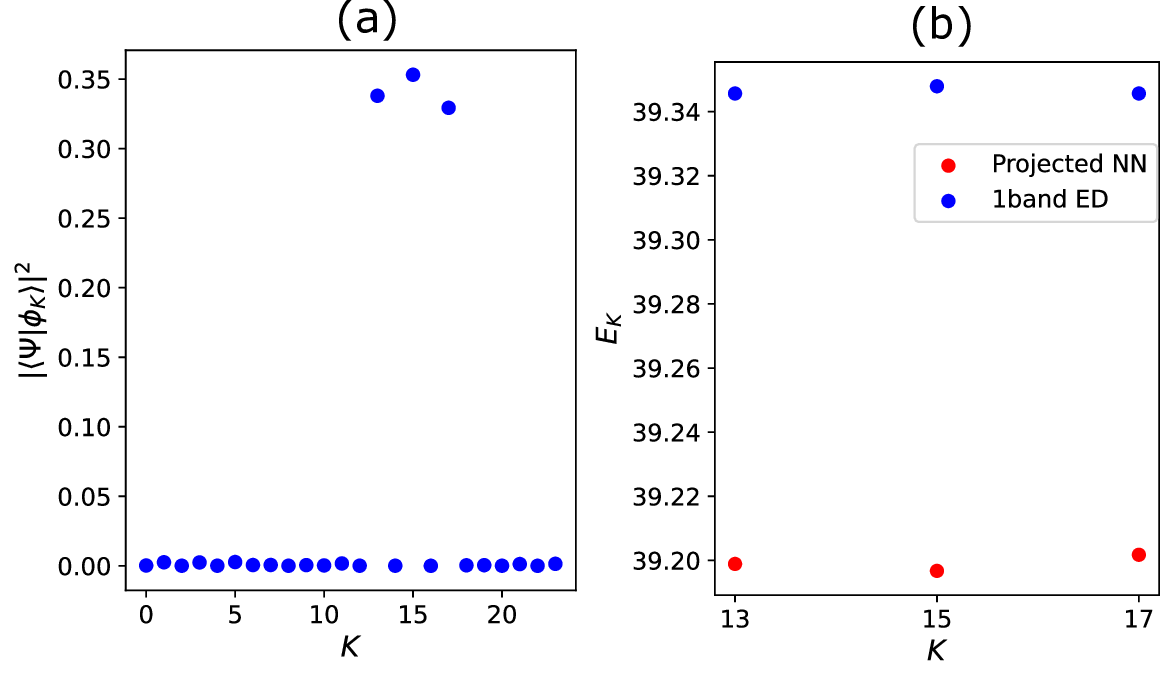
In this work, we present an efficient diagnostic of topological order that infers ground-state topological degeneracy from a single many-body wavefunction. Our method applies to translation-invariant systems, where degenerate ground states are labeled by many-body (crystal) momentum. We introduce a post-processing protocol that decomposes one optimized variational wavefunction into distinct momentum sectors, thereby producing a set of (nearly) degenerate ground states
This content is AI-processed based on open access ArXiv data.