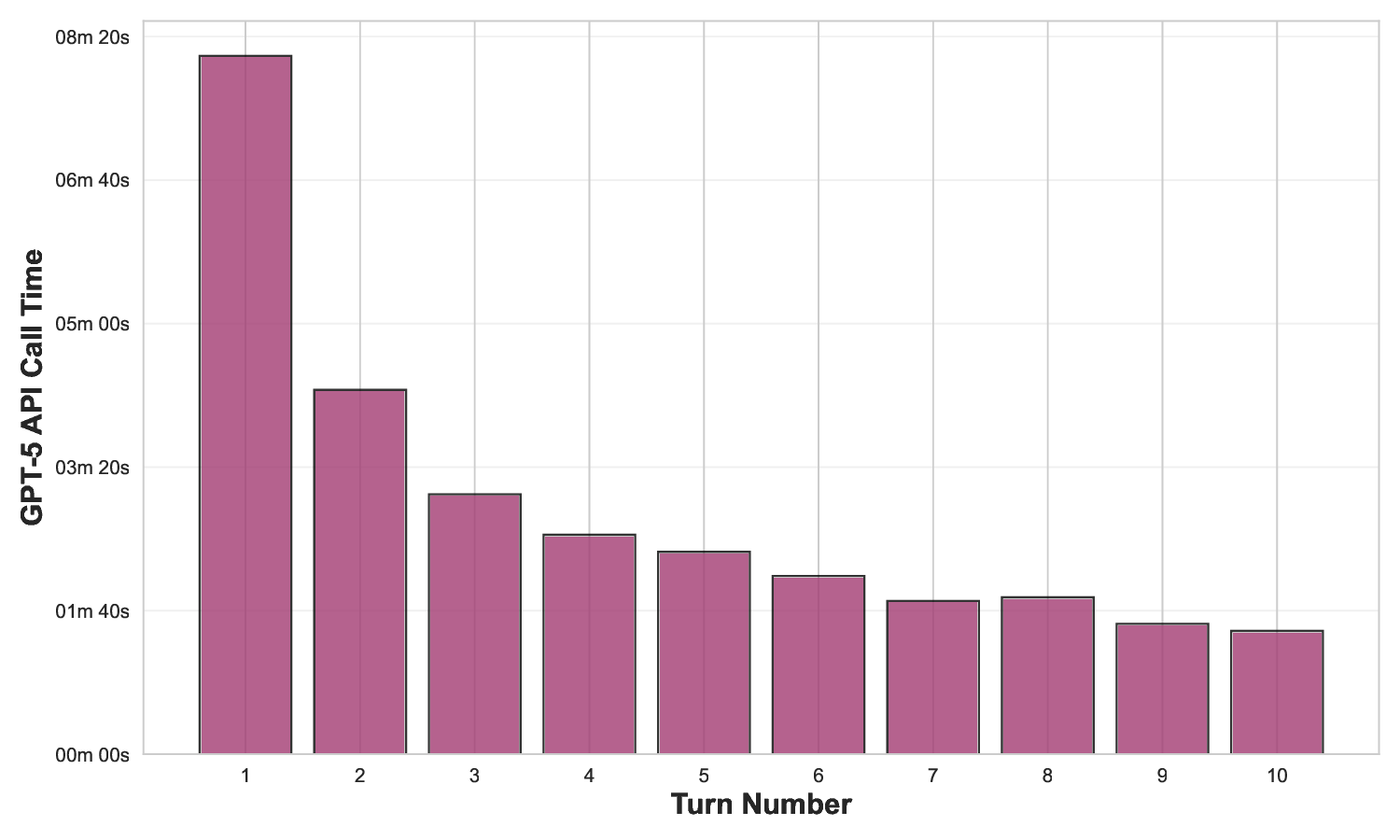
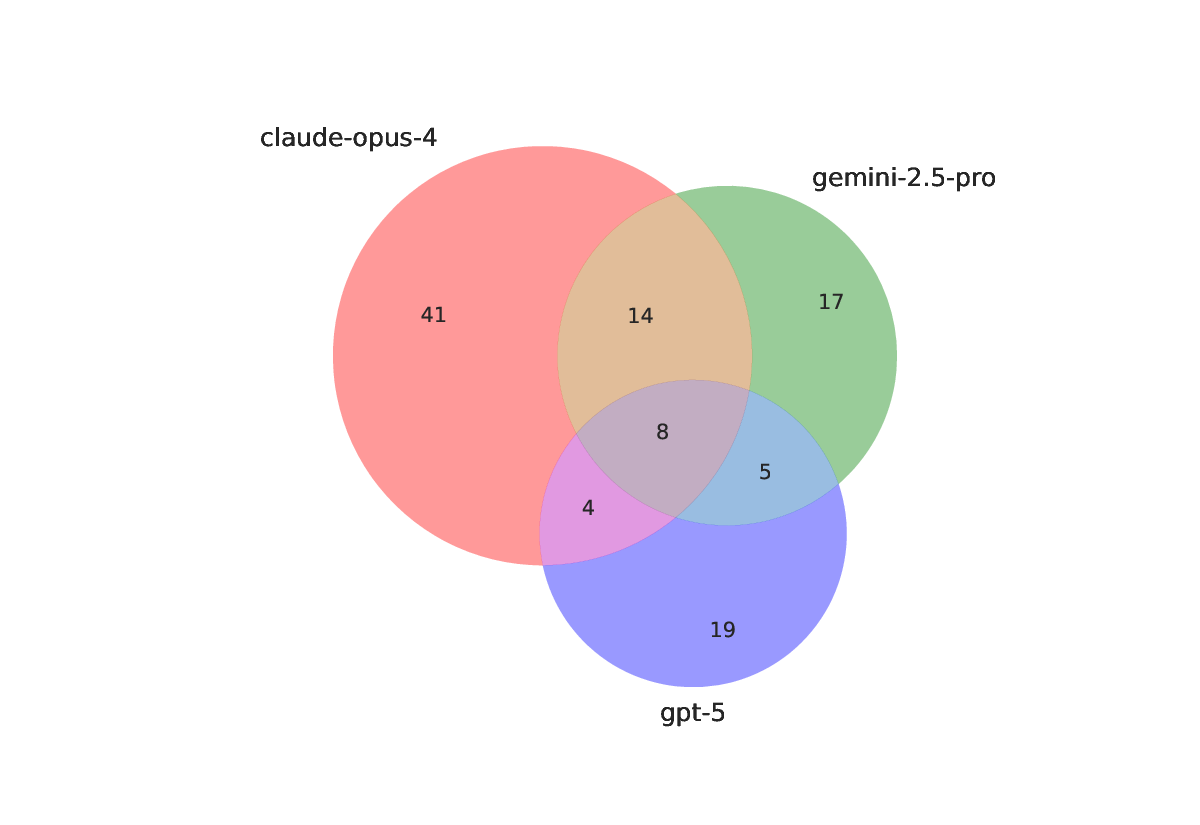
We introduce IndiMathBench, a human-verified benchmark designed to evaluate mathematical theorem proving, curated using an AI-powered human-assisted pipeline for formalizing natural language problems in Lean. IndiMathBench is composed of 312 formal Lean 4 theorems paired with their corresponding informal problem statements, sourced from Indian Mathematics Olympiads. Through category-based retrieval, iterative compiler feedback, and multi-model ensembles, our pipeline generates candidate formalizations that experts efficiently validate via an interactive dashboard with automated quality summaries. Evaluation across multiple frontier models demonstrates that autoformalization remains challenging, with substantial gaps between syntactic validity and semantic correctness, while theorem proving success rates remain low even with iterative refinement, demonstrating that \benchmark~presents a challenging testbed for mathematical reasoning. IndiMathBench is available at https://github.com/prmbiy/IndiMathBench.
The formalization of mathematics, expressing informal reasoning in precise, machine-verifiable logic, has been a long-standing goal in computer science and mathematics. A related task, autoformalization, seeks to automatically translate informal mathematical statements and proofs into formal representations (Wu et al., 2022;Agrawal et al., 2022a;Gadgil et al., 2022). Despite advances in large language models and theorem-proving frameworks such as Lean (Moura & Ullrich, 2021), progress remains limited by the scarcity of paired informal-formal data.
Let n be a natural number. Prove that: Existing benchmarks for formal theorem proving are few and narrow in scope. The largest Lean 4 benchmarks with Olympiad-level problems, MINIF2F (Zheng et al., 2022), drawn from AIME, AMC, and IMO exams, and Put-namBench (Tsoukalas et al., 2024), from the Putnam Competition, cover only a small fraction of the available competition mathematics, totaling roughly a thousand problems. This limited scale restricts comprehensive evaluation of model generalization and reasoning capabilities.
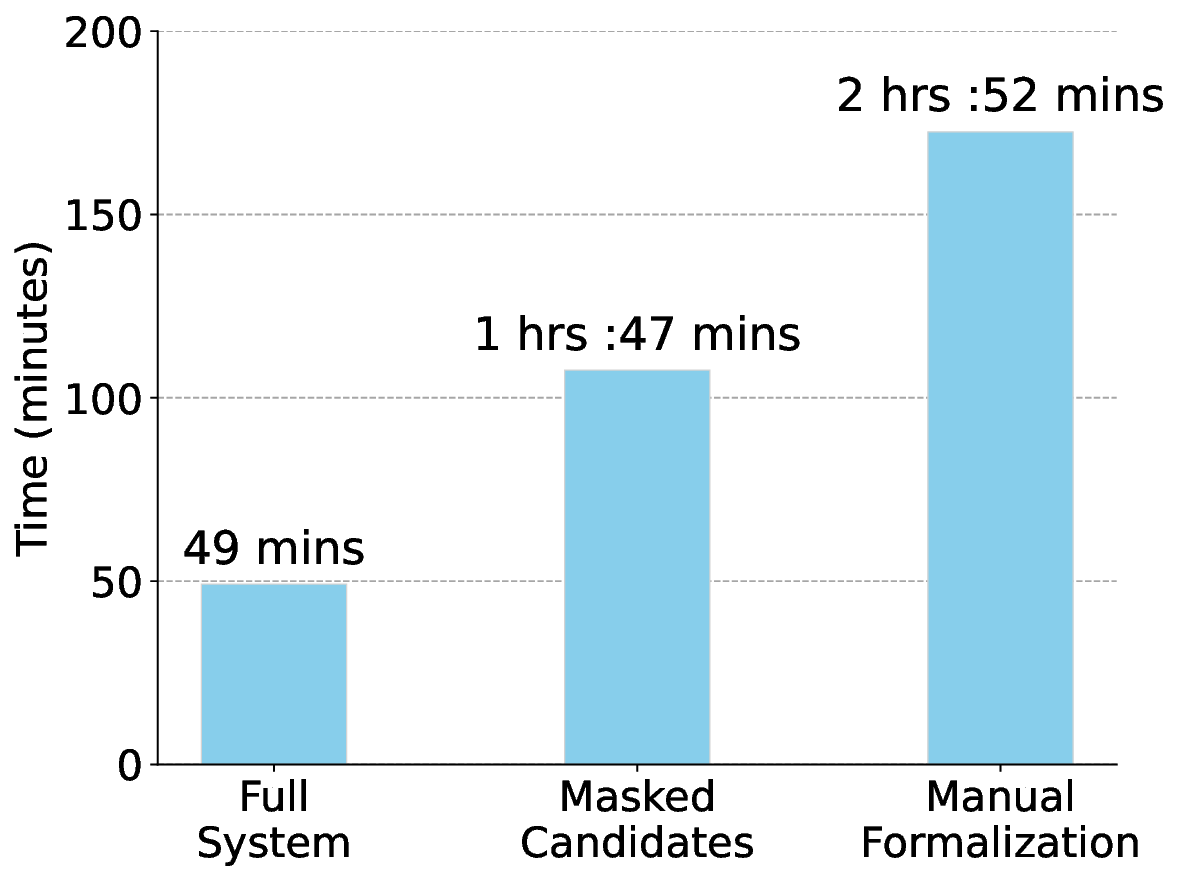
Moreover, these popular sources increasingly appear in large-scale pretraining corpora (Jiang et al., 2024), creating contamination that obscures genuine reasoning ability. Producing new benchmarks is further constrained by the high manual effort required: experts must formalize, annotate, and verify each problem in Lean, a process that is both time-consuming and resource-intensive (Yu et al., 2025). As a result, progress in ATP evaluation depends on developing scalable, high-quality, human-verified formal benchmarks. Also, despite LLMs’ improved syntax fidelity, their semantic alignment with mathematical intent remains poor. We hypothesize that human-AI collaborative formalization can bridge this gap.
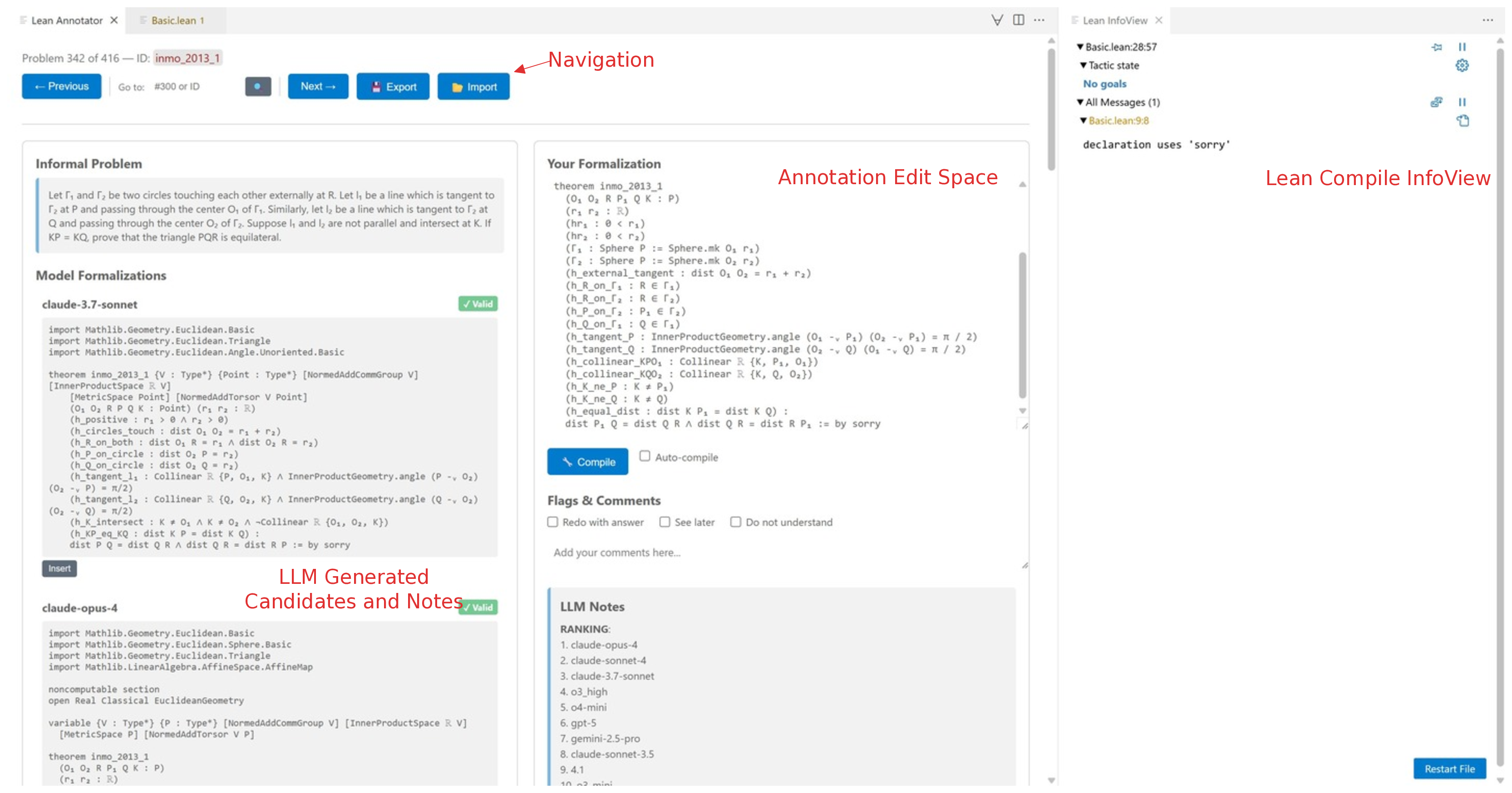
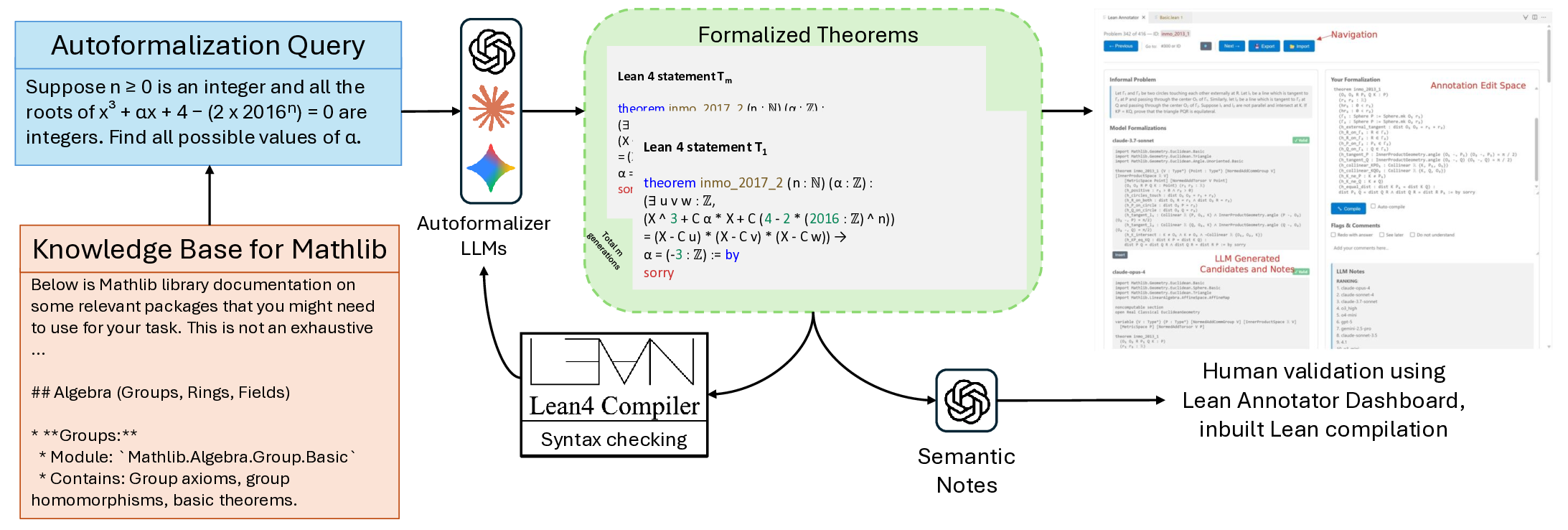
To address these challenges, we introduce INDIMATHBENCH , a human-verified benchmark for automated theorem proving built from Indian Mathematical Olympiad problems, built using a human-AI pipeline. Our benchmark contains 312 problems spanning diverse mathematical domains, geometry, algebra, number theory, and combinatorics, each paired with human-verified Lean 4 formalizations. A sample problem from INDIMATHBENCH is shown in Figure 1. We conducted systematic human verification of all formalizations, ensuring high-quality ground truth for reliable evaluation.
Our key contributions are:
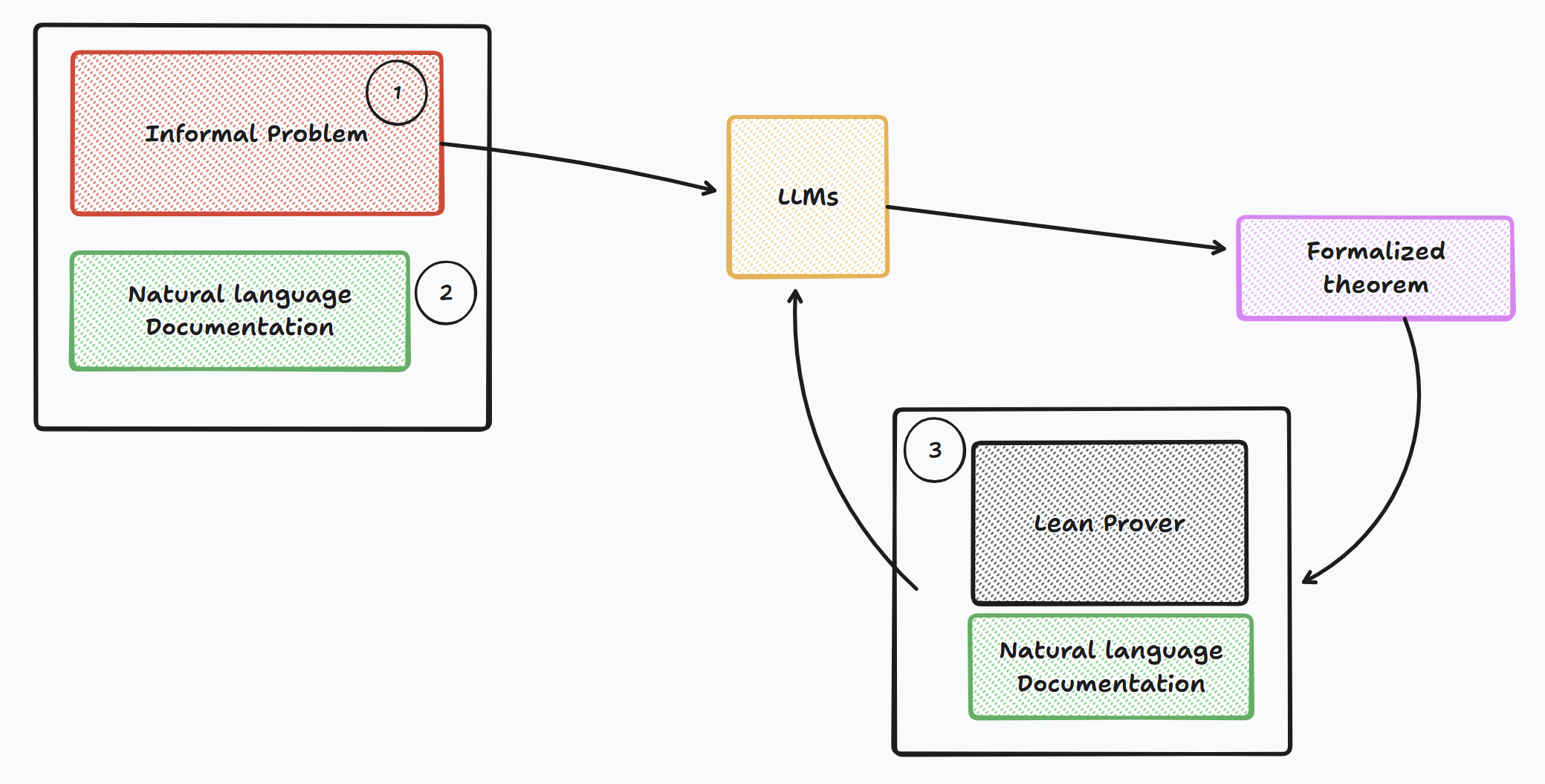
• A Lean 4 benchmark for formal theorem proving, created using LLM-assisted formalization and human verification. • A systematic formalization pipeline employing category-based retrieval, a self-debug loop, with an ensemble of LLMs, and cross comparison of formalizations and a controlled study on its efficacy gains. • A VS Code Extension for improved human-AI collaboration for Lean annotations.
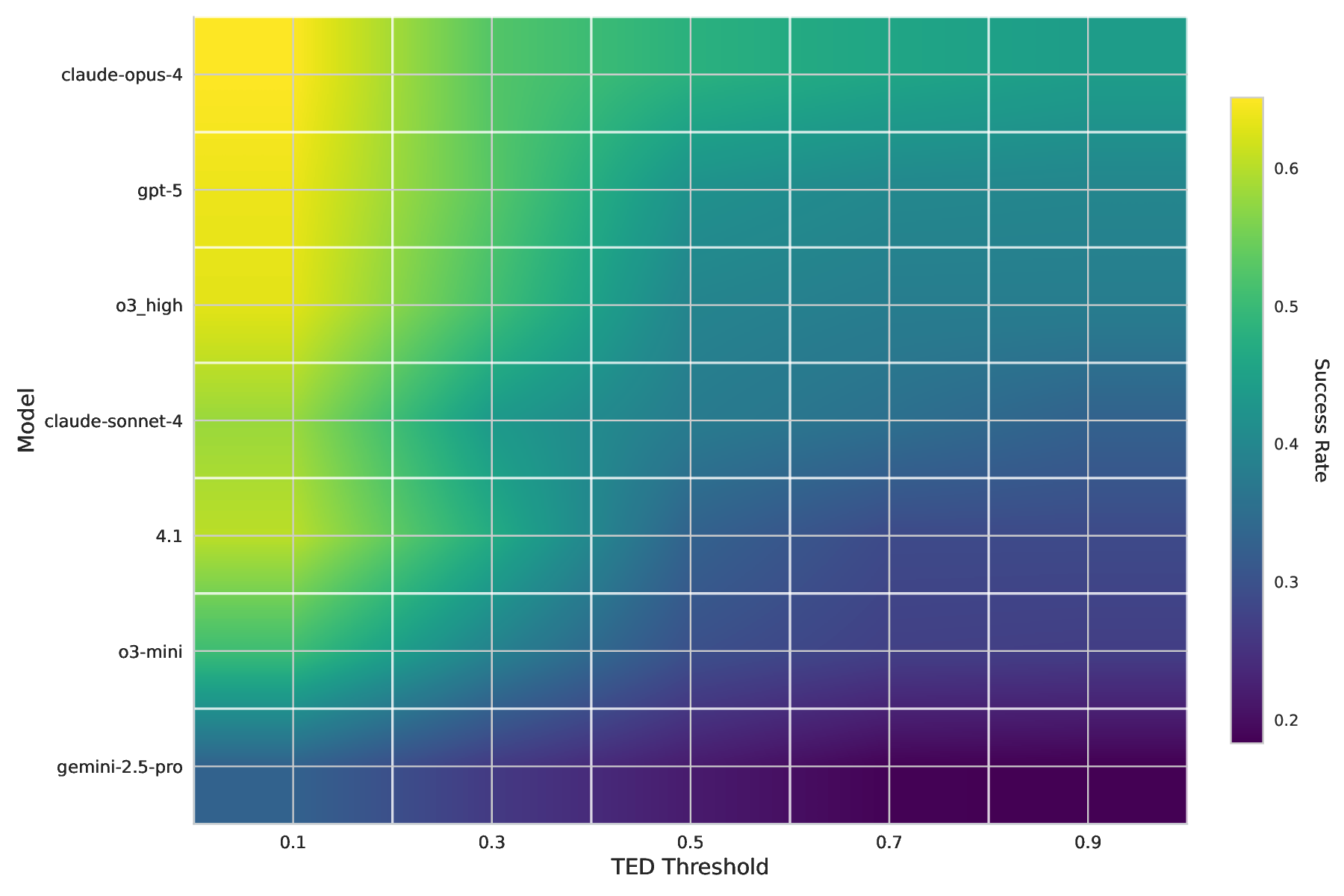
• Evaluation of frontier general purpose and fine-tuned models on their autoformalization and proving capabilities.
Formal Theorem Proving Benchmarks. The evaluation of automated theorem proving systems relies critically on curated formal benchmarks, yet existing resources remain limited in scale, diversity, and representativeness. The MINIF2F benchmark (Zheng et al., 2022), based on AMC, AIME, and IMO competitions, and PutnamBench (Tsoukalas et al., 2024), derived from the Putnam Competition, have become standard datasets for assessing Olympiad competition-level mathematical reasoning in Lean 4. More recent benchmarks such as ProofNet (Azerbayev et al., 2023) and FormalMath (Yu et al., 2025) focus on undergraduate or textbook-style mathematics, providing complementary but less challenging problem domains. While these resources have advanced systematic evaluation, they remain narrow in both mathematical coverage and cultural scope, largely reflecting Western curricula and competition traditions, where the focus is relatively less on geometry and combinatorics style problems, and more towards analysis, algebra and number theory. Recent efforts like FrontierMath (Glazer et al., 2025) extend evaluation toward research-level problems but reveal extremely low model success rates, underscoring the substantial gap between current benchmarks and the diversity of human mathematical reasoning, but doesn’t support Lean.
In particular, Olympiad-style geometry and combinatorics remain strikingly underrepresented across all existing Lean 4 benchmarks. Even the most widely used Olympiad datasets contain only a small number of high-difficulty geometry problems, despite these being among the hardest domains for both ATPs and LLM-guided provers. Recent efforts such as LeanGeo (Song et al., 2025) and Com-biBench (Liu et al., 2025a) were motivated by this same gap, indicating that it is a well-recognized limitation in the formalization ecosystem for geometry and combinatorics respectively. This imbalance limits the ability of current benchmarks to stress-test systems on categories that are disproportionately challenging.
Autoformalization. Autoformalization aims to translate informal math
This content is AI-processed based on open access ArXiv data.