A common recipe to improve diffusion models at test-time so that samples score highly against a user-specified reward is to introduce the gradient of the reward into the dynamics of the diffusion itself. This procedure is often ill posed, as user-specified rewards are usually only well defined on the data distribution at the end of generation. While common workarounds to this problem are to use a denoiser to estimate what a sample would have been at the end of generation, we propose a simple solution to this problem by working directly with a flow map. By exploiting a relationship between the flow map and velocity field governing the instantaneous transport, we construct an algorithm, Flow Map Trajectory Tilting (FMTT), which provably performs better ascent on the reward than standard test-time methods involving the gradient of the reward. The approach can be used to either perform exact sampling via importance weighting or principled search that identifies local maximizers of the reward-tilted distribution. We demonstrate the efficacy of our approach against other look-ahead techniques, and show how the flow map enables engagement with complicated reward functions that make possible new forms of image editing, e.g. by interfacing with vision language models.
Large scale foundation models built out of diffusions (Ho et al., 2020;Song et al., 2020) or flowbased transport (Lipman et al., 2022;Albergo & Vanden-Eijnden, 2022;Albergo et al., 2023;Liu et al., 2022) have become highly successful tools across computer vision and scientific domains. In this paradigm, performing generation amounts to numerically solving an ordinary or stochastic differential equation (ODE/SDE), the coefficients of which are learned neural networks. An active area of current research is how to best adapt these dynamical equations at inference time to extract samples from the model that align well with a user-specified reward. For example, as shown in Figure 1, a user may want to generate an image of a clock with a precise time displayed on it, which is often generated inaccurately without suitable adaptation of the generative process. These approaches, often collectively referred to as guidance, do not require additional re-training and as a result are orthogonal to the class of fine-tuning methods, which instead attempt to adjust the model itself via an additional learning procedure to modify the quality of generated samples.
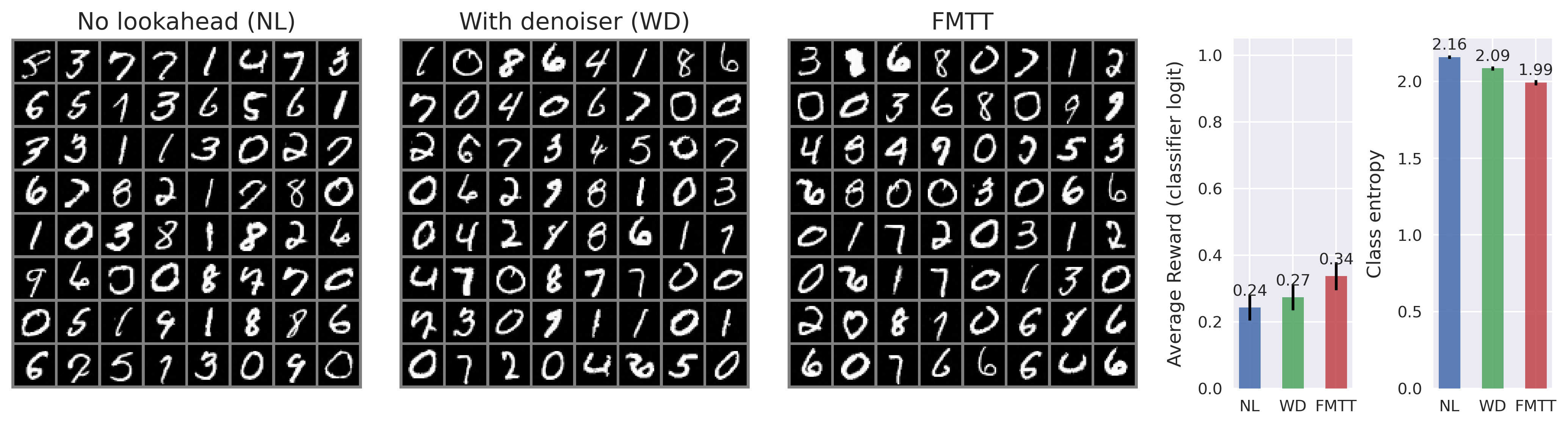
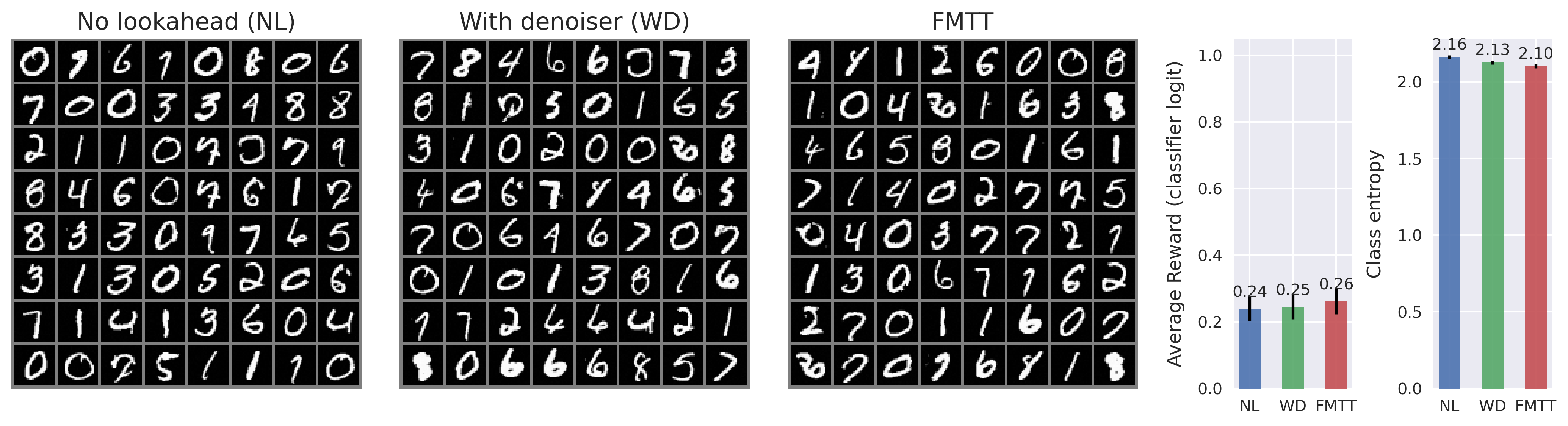
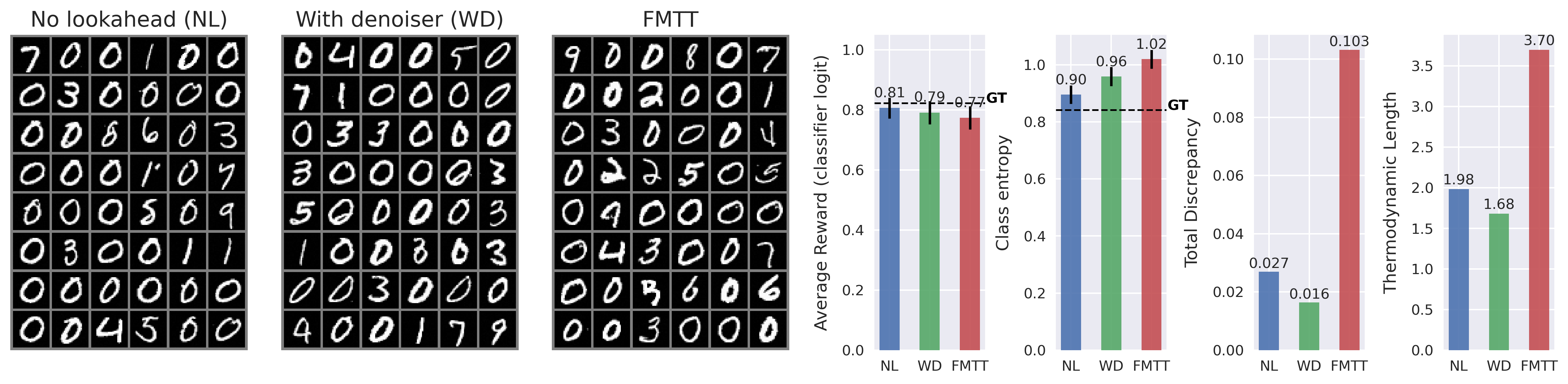
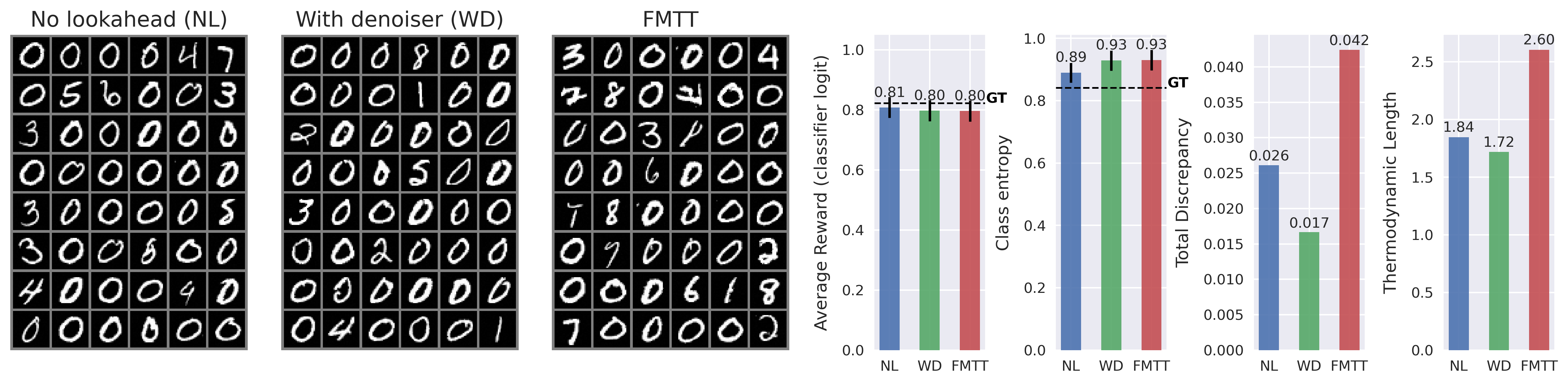
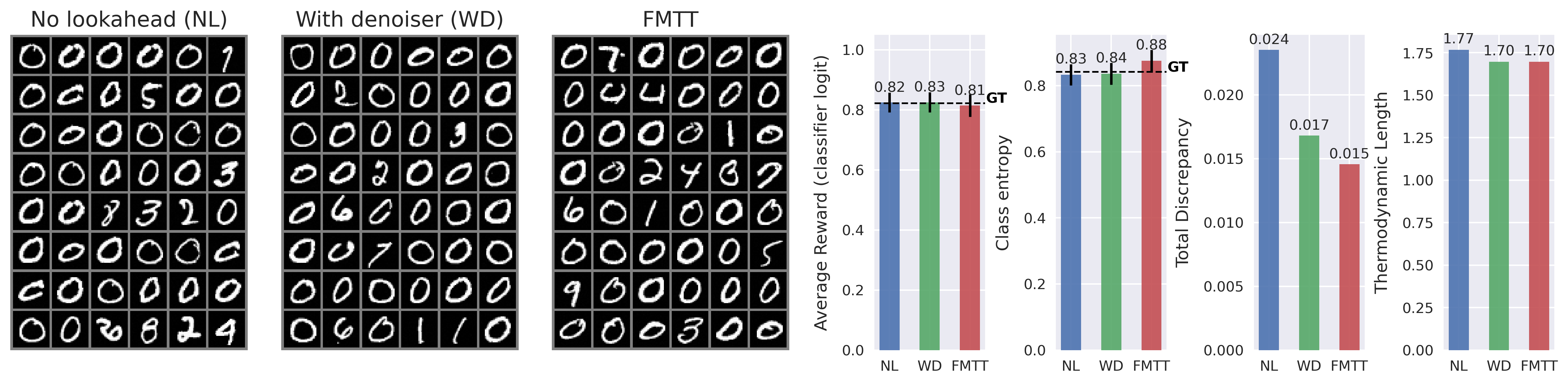
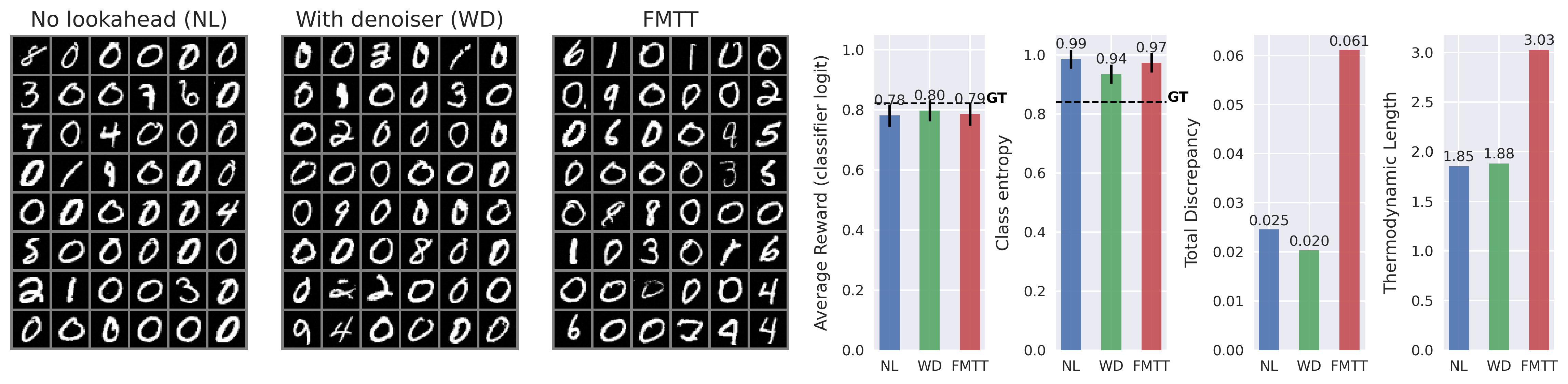
While guidance-based approaches can often be made to work well in practice, most methods are somewhat ad-hoc, and proceed by postulating a term that may drive the generative equations towards the desired goal. To this end, a common approach is to incorporate the gradient of the reward model, which imposes a gradient ascent-like structure on the reward throughout generation. Despite the intuitive appeal of this approach, typical rewards are defined only at the terminal point of generation -i.e., over a clean image -rather than over the entire generative process. This creates a need to “predict” where the current trajectory will land, in principle necessitating an expensive additional differential equation solve per step of generation. To avoid the associated computational expense of this nested solve, common practice is to employ a heuristic approximation of the terminal point, such as leveraging a one-step denoiser that can be derived from a learned score-or flow-based model. See Figure 2 for visualizations of the one-step denoiser across different noise levels. In this paper, we revisit the reward guidance problem from the perspective of flow maps, a recently-introduced methodology for flow-based generative modeling that learns the solution operator of a probability flow ODE directly rather than the associated drift (Boffi et al., 2024;2025;Sabour et al., 2025;Geng et al., 2025). By leveraging a simple identity of the flow map, we show that an implicit flow can be used to define a reward-guided generative process as in the case of standard flow-based models. With access to the flow map in addition to the implicit flow, we can predict the terminal point of a trajectory in a single or a few function evaluations, vastly improving the prediction relative to denoiser-based techniques -see again Figure 2 -and leading to significantly improved optimization of the reward. In addition, we highlight how to incorporate time-dependent weights throughout the generative process to account for the gradient ascent’s failure to equilibrate on the timescale of generation, leading to several new and effective ways to sample high-reward outputs.
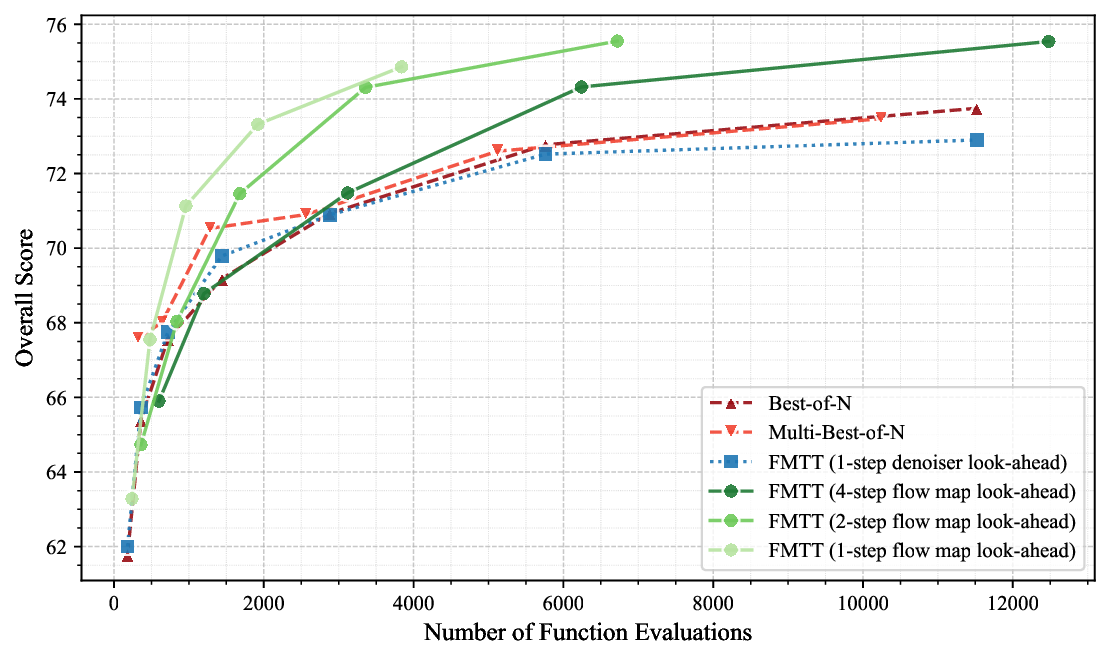
Contributions. (i) We introduce Flow Map Trajectory Tilting (FMTT), a principled inference time adaptation procedure for flow maps that effectively uses their look-ahead capabilities to accurately incorporate learned and complex reward functions in Monte Carlo and search algorithms. (ii) Using conditions that characterize the flow map, we show that the importance weights for this Jarzynski/SMC scheme reduce to a remarkably simple formula. Our approach is theoretically grounded in controlling the thermodynamic length of the process over baselines, a measure of the efficiency of the guidance in sampling the tilted distribution. (iii) We empirically show that FMTT has favorable test-time scaling characteristics that outperform standard ways of embedding rewards into diffusion sampling setups. (iv) To our knowledge, we demonstrate the first successful use of pretrained dx t = v t,t (x t )dt + ϵ t [ s t (x t )+ ∇r t (X t,1 (x t )) ] dt + 2ϵ t dW t dA t = r(X t,1 (x t ))dt ∇r t (X t,1 (x t )) exac t look ahea d X t,1 (x t ) ρ 0 ρ 1 ρ 1 ∼ρ 1 (x)e r(x) SMC Resampling t = 1 t = 0 Time t
Figure 3: Schematic overview of test-time adaptation of diffusions with flow map tilting. Using the look-ahead map Xt,1(xt) in the diffusion inside the reward, reward information can be principly used through the tilted trajectories (green lines). This allows us to perform better ascent on the reward, and the importance weights At take on a remarkably simple form that can be used for both exactly sampling ρt and search for maximizers of ρt.
vision-language models (VLMs) as reward functions for test-time scaling, allowing rewards to be specified entirely in natural la
This content is AI-processed based on open access ArXiv data.