Large Language Models (LLMs) are known for their expensive and time-consuming training. Thus, oftentimes, LLMs are fine-tuned to address a specific task, given the pretrained weights of a pre-trained LLM considered a foundation model. In this work, we introduce memory-efficient, reversible architectures for LLMs, inspired by symmetric and symplectic differential equations, and investigate their theoretical properties. Different from standard, baseline architectures that store all intermediate activations, the proposed models use time-reversible dynamics to retrieve hidden states during backpropagation, relieving the need to store activations. This property allows for a drastic reduction in memory consumption, allowing for the processing of larger batch sizes for the same available memory, thereby offering improved throughput. In addition, we propose an efficient method for converting existing, non-reversible LLMs into reversible architectures through fine-tuning, rendering our approach practical for exploiting existing pre-trained models. Our results show comparable or improved performance on several datasets and benchmarks, on several LLMs, building a scalable and efficient path towards reducing the memory and computational costs associated with both training from scratch and fine-tuning of LLMs.
1. Introduction. Large Language Models (LLMs) have achieved remarkable success in natural language processing, powering breakthroughs across diverse applications [6,20]. However, their rapid scaling has introduced critical computational bottlenecks-chief among them is the excessive memory consumption during training and fine-tuning.
That limitation is common to most Transformer-based architectures, that require storing intermediate activations, to enable gradient computation via backpropagation. As a result, memory usage grows linearly with depth, significantly constraining the training of deep models and their deployment and training on resource-limited hardware. This limitation not only restricts model size, but also forces smaller batch sizes, which increases training time by requiring more iterations and communication to process the same dataset.
To address this limitation, we draw inspiration from time-reversible physical systems such as wave propagation, advection, and Hamiltonian flows [19,13,9]. In particular, we generalize and extend recent advances in reversible vision transformers [22,17] to the language modeling domain. We alleviate the memory limitation by introducing a family of reversible architectures for LLMs based on hyperbolic differential equations, implemented through learned reversible dynamics.
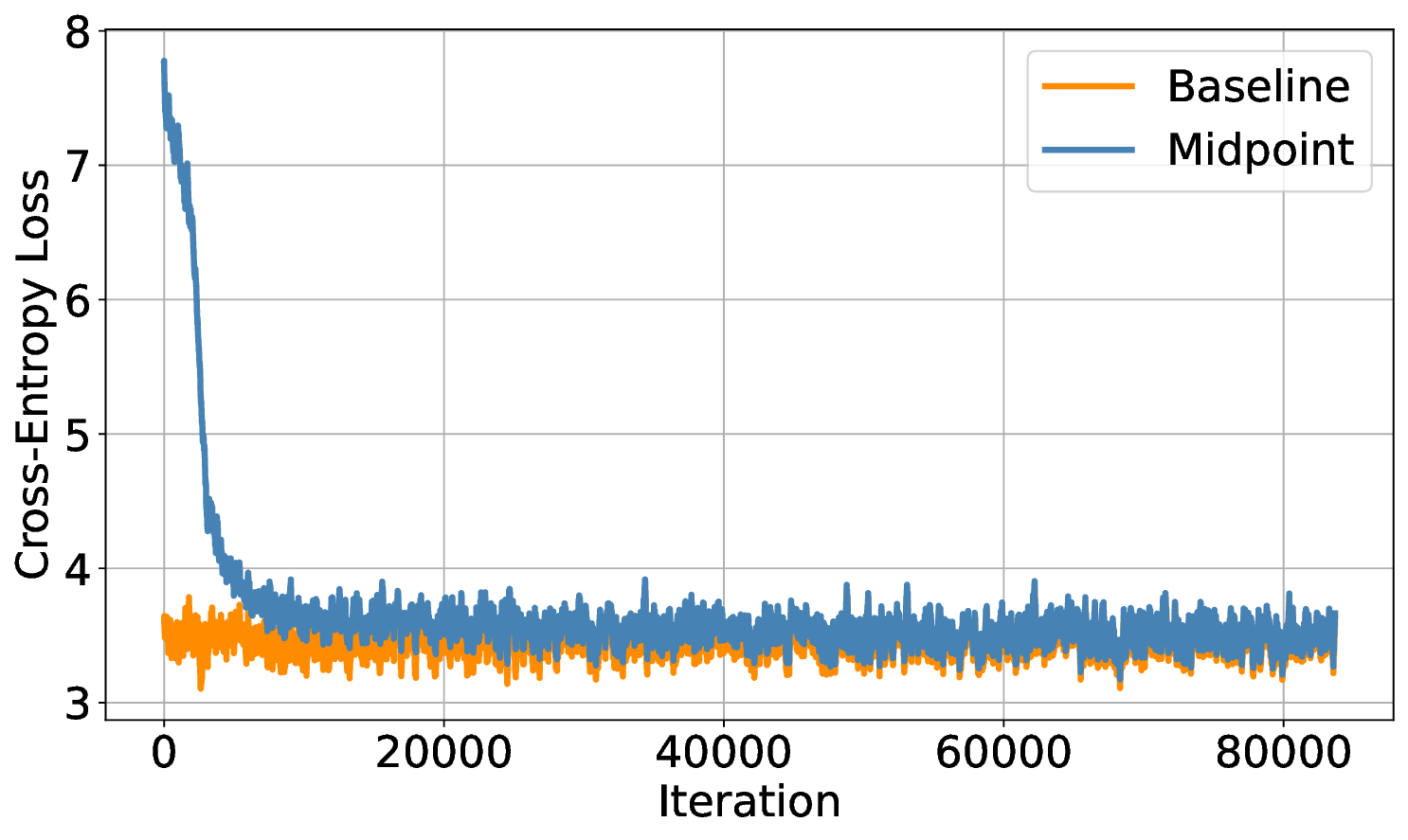
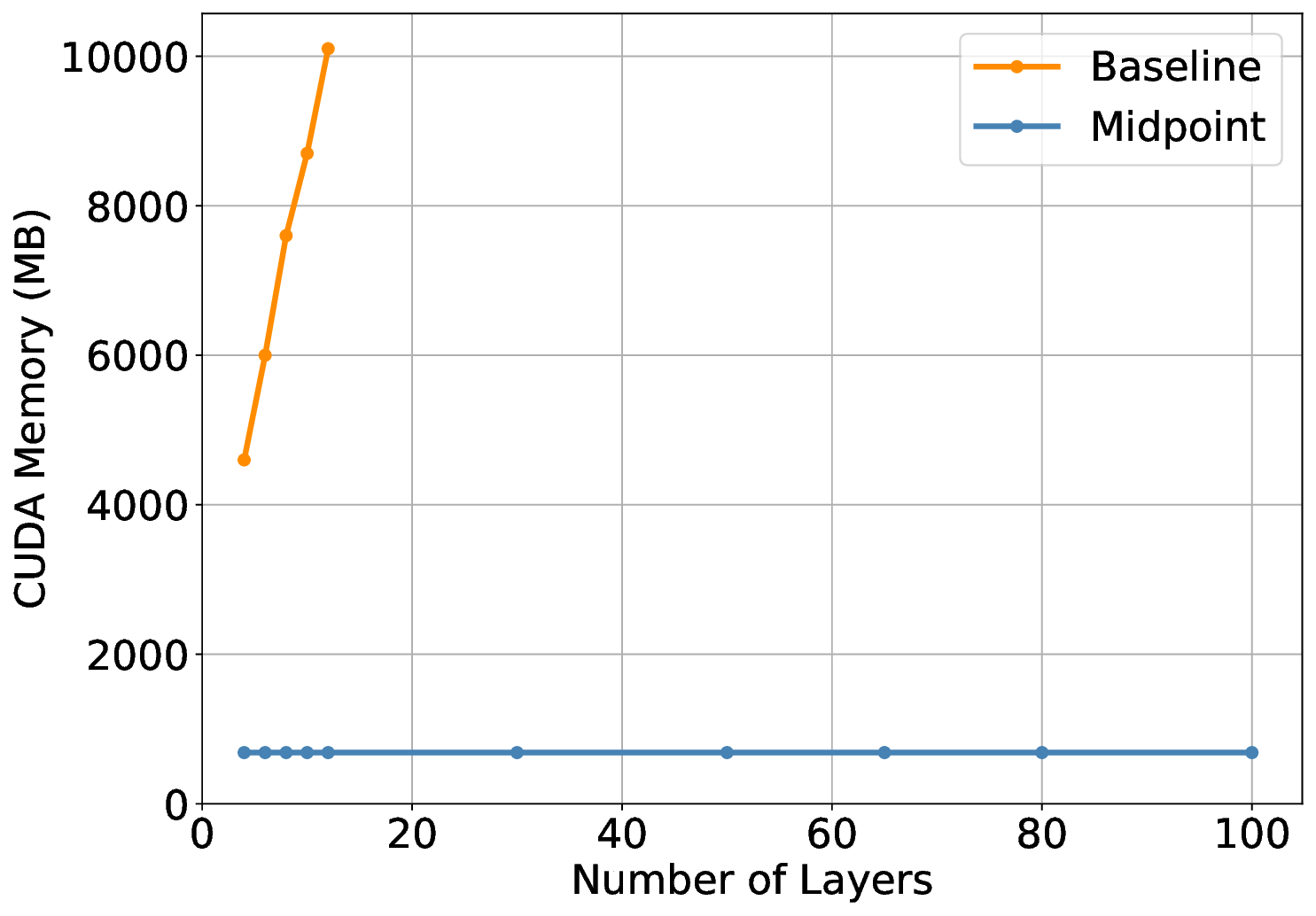
A core advantage of our approach is that our architectures are reversible by design, allowing the backward pass to reconstruct intermediate activations without storing them during the forward pass. This drastically reduces memory requirements by an order of magnitude, enabling larger batch sizes and thereby significantly improving training throughput. Although reversible methods incur a modest increase in floatingpoint operations, we show that due to the increase in throughput, the memory savings compensate for the additional computations, reducing wall-clock training time under fixed computational budgets. In summary, training a reversible network results in a reduction in computational time. This idea is similar to “Activation Recomputation” [16], the difference is that our reversible network does not require storing any activations.
Another distinctive property of our architectures, which are based on hyperbolic PDEs, is their ability to conserve energy over time, in contrast to parabolic systems such as diffusion-based networks, which dissipate energy as depth increases [7,11,12]. By modeling token dynamics as conservative flows, our architectures preserve the fidelity of representations across depth, making them more scalable. This inductive bias supports stable long-range information propagation and enables the conceptual design of models with infinite effective depth.
Lastly, although reversible architectures offer several advantages, there remain many scenarios where fine-tuning a large non-reversible model for a specific task using limited resources is desirable. To address this, we propose a novel method for retrofitting pre-trained non-reversible models into reversible ones. By leveraging a structural correspondence between reversible dynamics and standard residual updates, we show that only minimal fine-tuning is required to enable reversible execution. This provides a practical approach to memory-efficient fine-tuning under resource constraints.
Our contributions are summarized as follows:
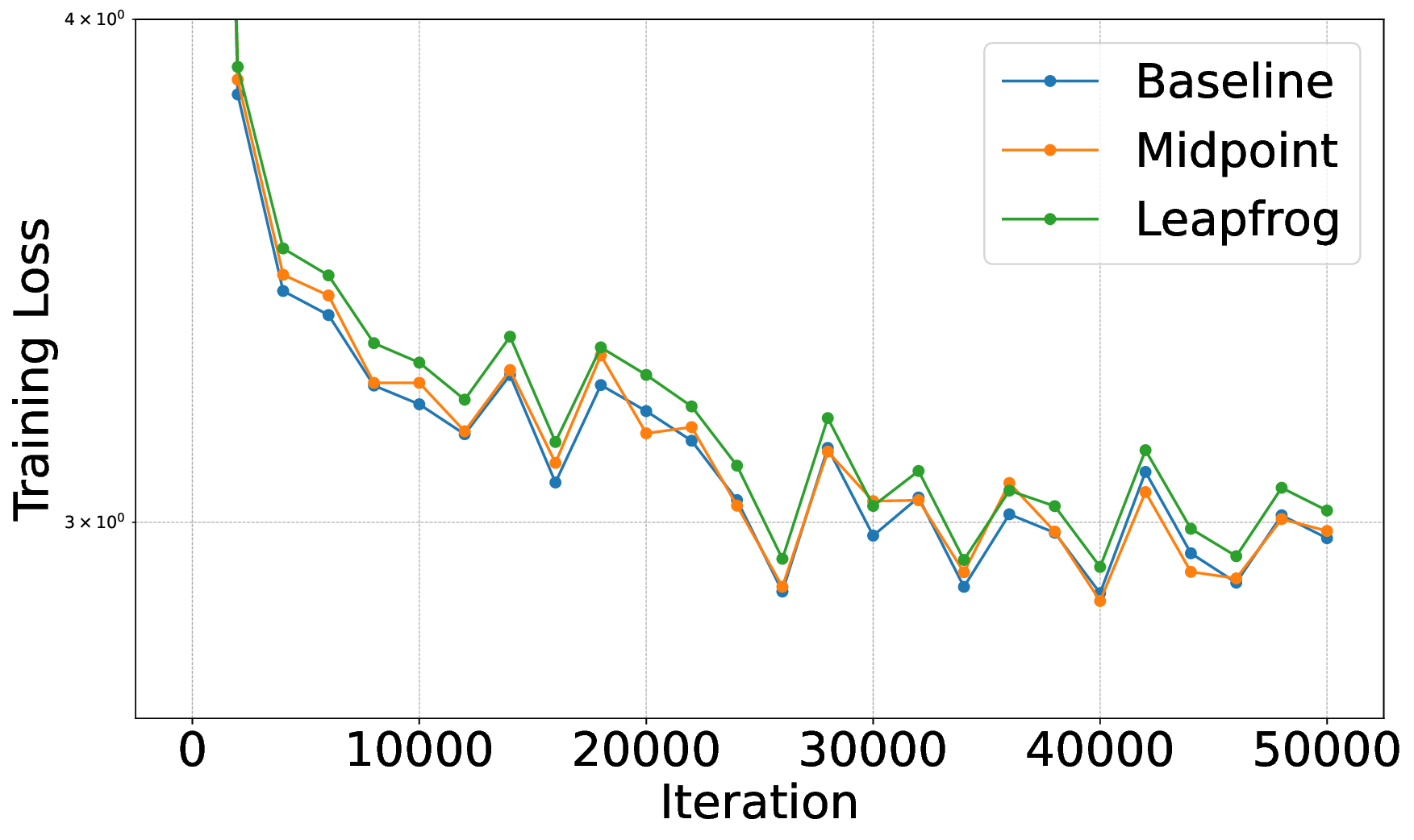
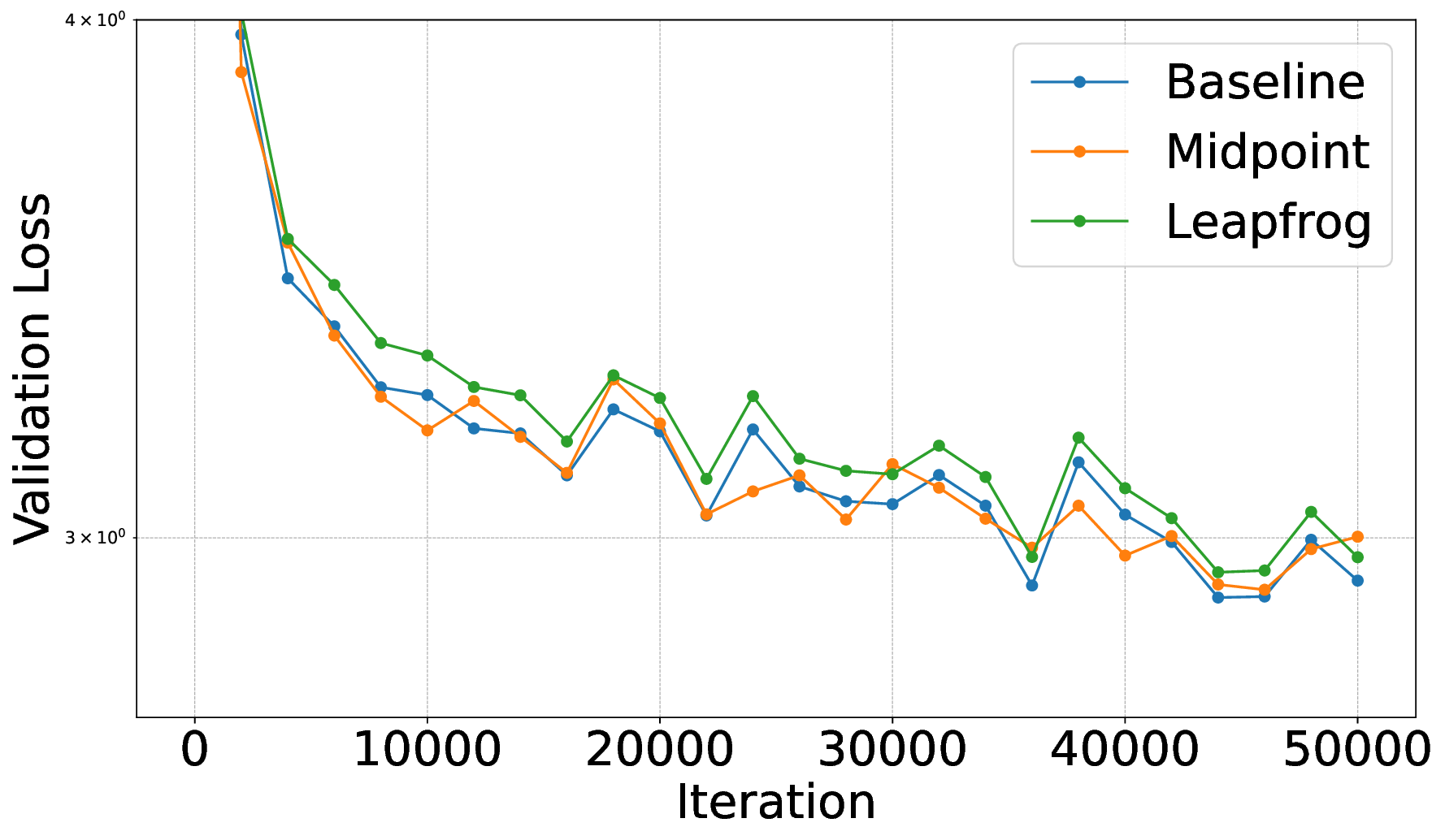
• We propose a new class of reversible language model architectures derived from hyperbolic differential equations, leveraging conservative discretizations that preserve information flow and guarantee reversibility. We further study their theoretical properties. • We demonstrate that these models are invertible by construction, enabling memory-efficient training that supports larger batch sizes and enhances throughput. • We present a mechanism for retrofitting pre-trained non-reversible baseline models into reversible architectures via fine-tuning compatible with existing LLMs. • We present an empirical evaluation of our reversible models, including both training from scratch and retrofitting baseline models into reversible architectures. Our results demonstrate competitive or improved performance, highlighting not only the computational efficiency of reversible LLMs but also their effectiveness on downstream tasks.
- Reversible Large Language Models. In this section, we introduce our reversible LLMs. We start with an overview of existing, non-reversible architectures, followed by a formal definition of reversible LLMs. We then discuss the memory footprint of our models, followed by a discussion of their expressiveness and downstream performance compared with standard architectures.
Common Network Architecture Overview. Modern language models are typically structured in three main stages: (i) an input embedding layer; (ii) a deep core of repeated Transformer layers; (iii) a final projection layer.
Given a tokenized input sequence x = (x 1 , x 2 , . . . , x T ), x i ∈ N, the model first
This content is AI-processed based on open access ArXiv data.