In the context of global climate change, geological materials are increasingly destabilized by water flow and infiltration. We study the creeping dynamics of a densely monitored landslide in Western Norway to decipher the role of fluid flow in destabilizing this landslide. In {\AA}knes, approximately 50 million cubic meter of rock mass continuously creeps over a shear zone made of rock fragments, with seasonal accelerations that strongly correlate with rainfall. In this natural laboratory for fluid-induced frictional creep, unprecedented monitoring equipment reveals low fluid pressure across the shear zone, thereby challenging the dominant theory of fluid-driven instability in landslides. Here, we show that a generic micromechanical model can disentangle the effects of fluid flow from those of fluid pressure, and demonstrate that seepage forces applied by channelized flow along the shear zone are the main driver of creep accelerations. We conclude by discussing the significance of seepage forces, the implications for hazard mitigation and the broader applicability of our model to various geological contexts governed by friction across saturated shear zones.
The stability of natural slopes is a critical concern in the context of climate change, as precipitations and fluid infiltration increasingly perturb landslides worldwide. The zones of weakness along which slopes deform are typically made of unconsolidated debris and clay-rich material. Often these granular shear zones do not stand still and commonly deform at a slow creep rate, in the range of millimetres to centimetres per year [1][2][3][4][5]. This slow and mostly aseismic deformation may be punctuated by short-lived accelerations called creep bursts. These bursts are often driven by intense rainfall or snow melt, accumulating strain that may precede runaway failure [6][7][8][9]. Understanding how fluids interact with the granular shear zones of landslides is therefore essential for linking rainfall and snow-melt to landslide dynamics and for hazard assessment and mitigation.
For decades, the dominant framework has been Terzaghi’s effective-stress theory, in which elevated pore fluid pressure reduces the normal stress and thereby weakens the frictional resistance of soils and rocks [10]. The effect of pore fluid pressurization is expected to play a major role in both the initiation and acceleration preceding failure of landslides [11][12][13][14][15]. Yet, in the context of creeping landslides, recent in-situ measurements reveal how rainfall-induced creep bursts arise with negligible fluid pressure in the shear zones [16], suggesting that pore pressure alone cannot always account for the observed seasonal creep bursts. This discrepancy motivates consideration of an additional hydro-mechanical effect, that of seepage force exerted by water flow within a granular shear zone.
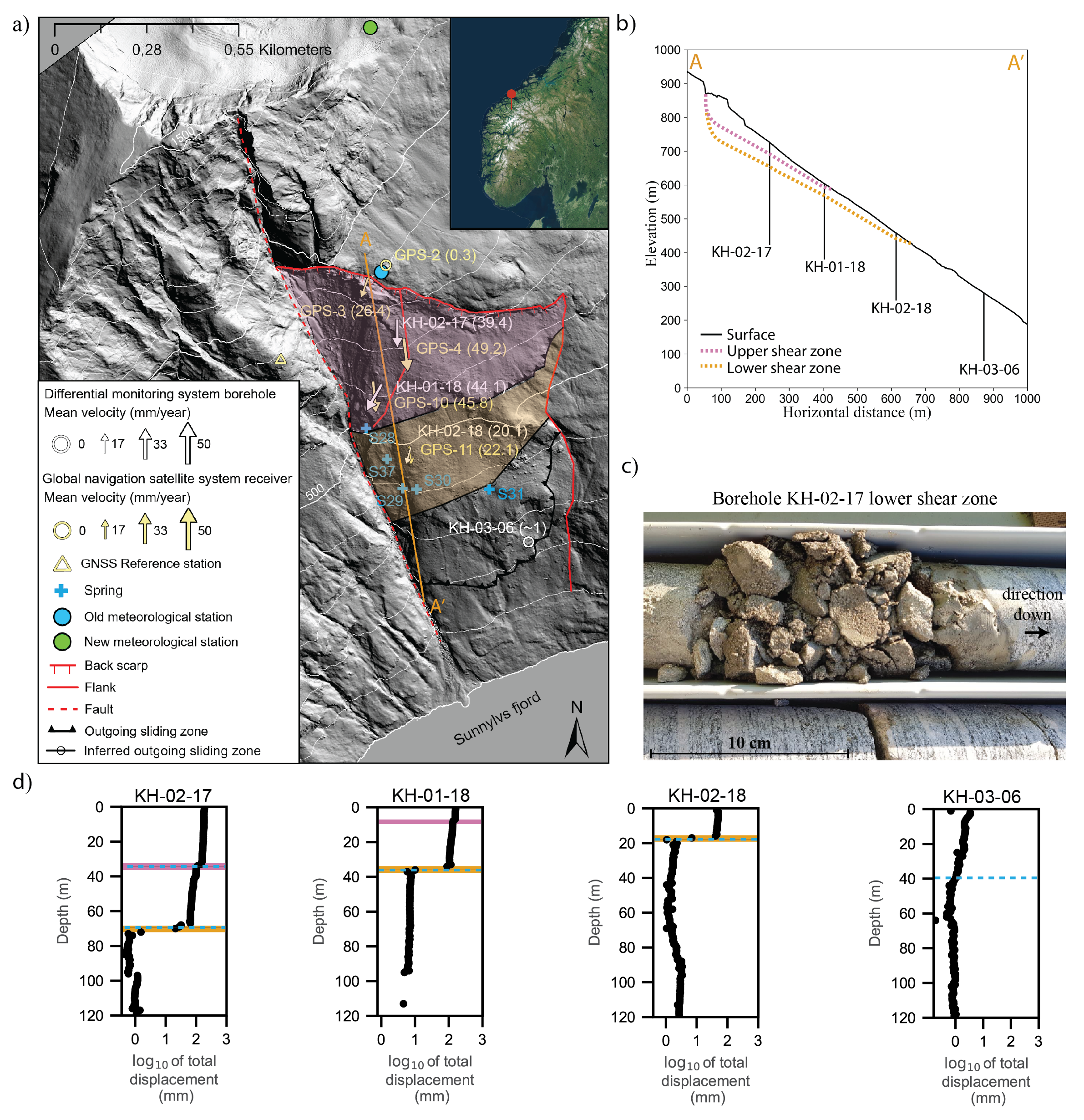
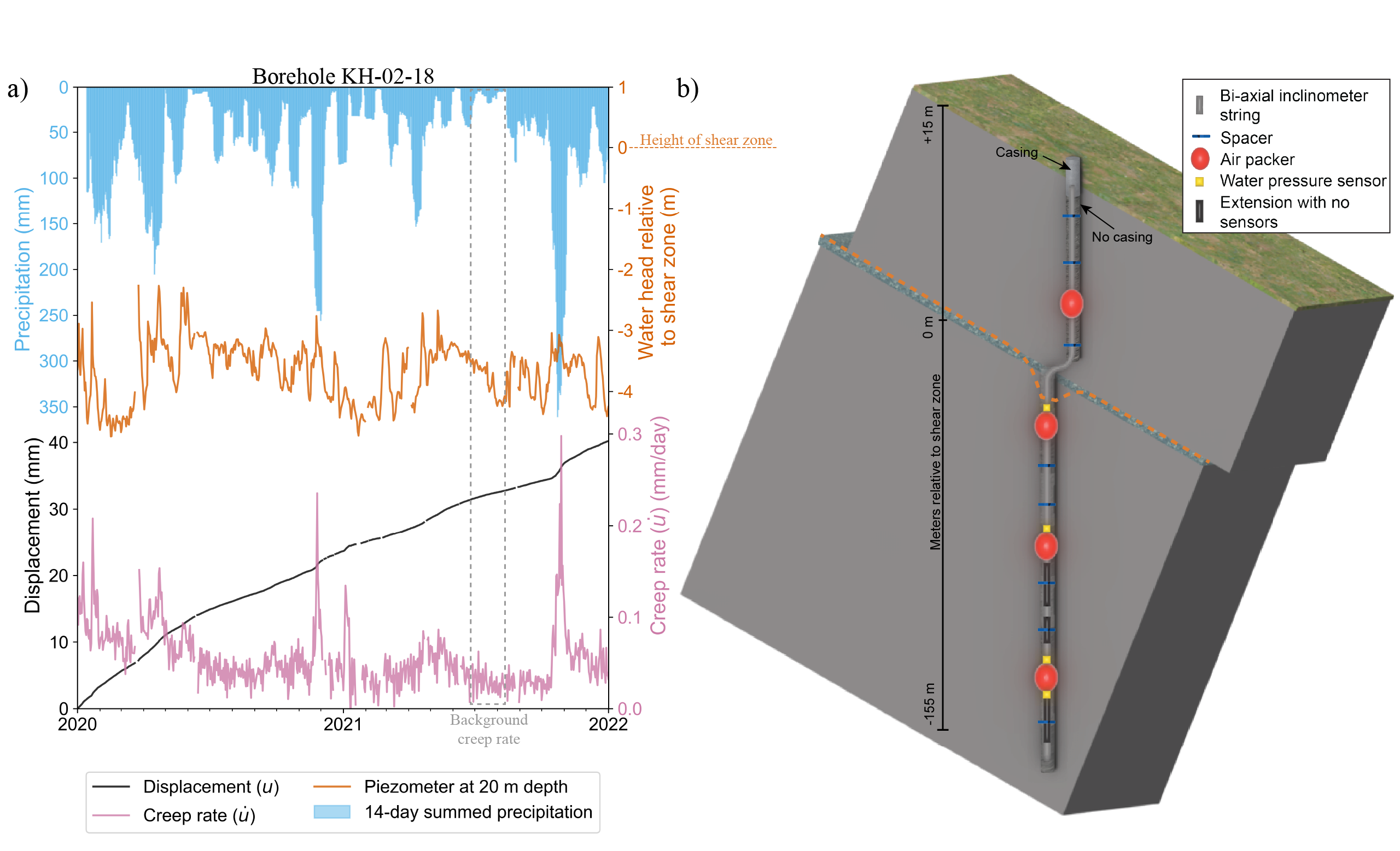
To disentangle and clarify the full spectrum of hydro-mechanical forces, we develop a generic mechanical model, combining basic stress balance with granular and fluid flow in a creeping granular shear zone, Fig 1 . The model separates hydrostatic pressurization from flow-induced seepage forces and tests their respective impacts on landslide creep rates. To evaluate the model, we apply it to a creeping landslide in Norway. This natural laboratory offers a unique opportunity to test our approach due to three key features: (1) displacement is localized on shear zones comprising debris and clay-rich material; (2) the landslide exhibits seasonal creep bursts that correlate with intense rainfall events; and (3) deformation is monitored using stateof-the-art high-resolution instrumentation mounted in an array of boreholes. Despite low fluid pressures, visual evidence indicates significant fluid flow through the shear zones, supporting the relevance of seepage-driven dynamics (see video in Supplemental Material).
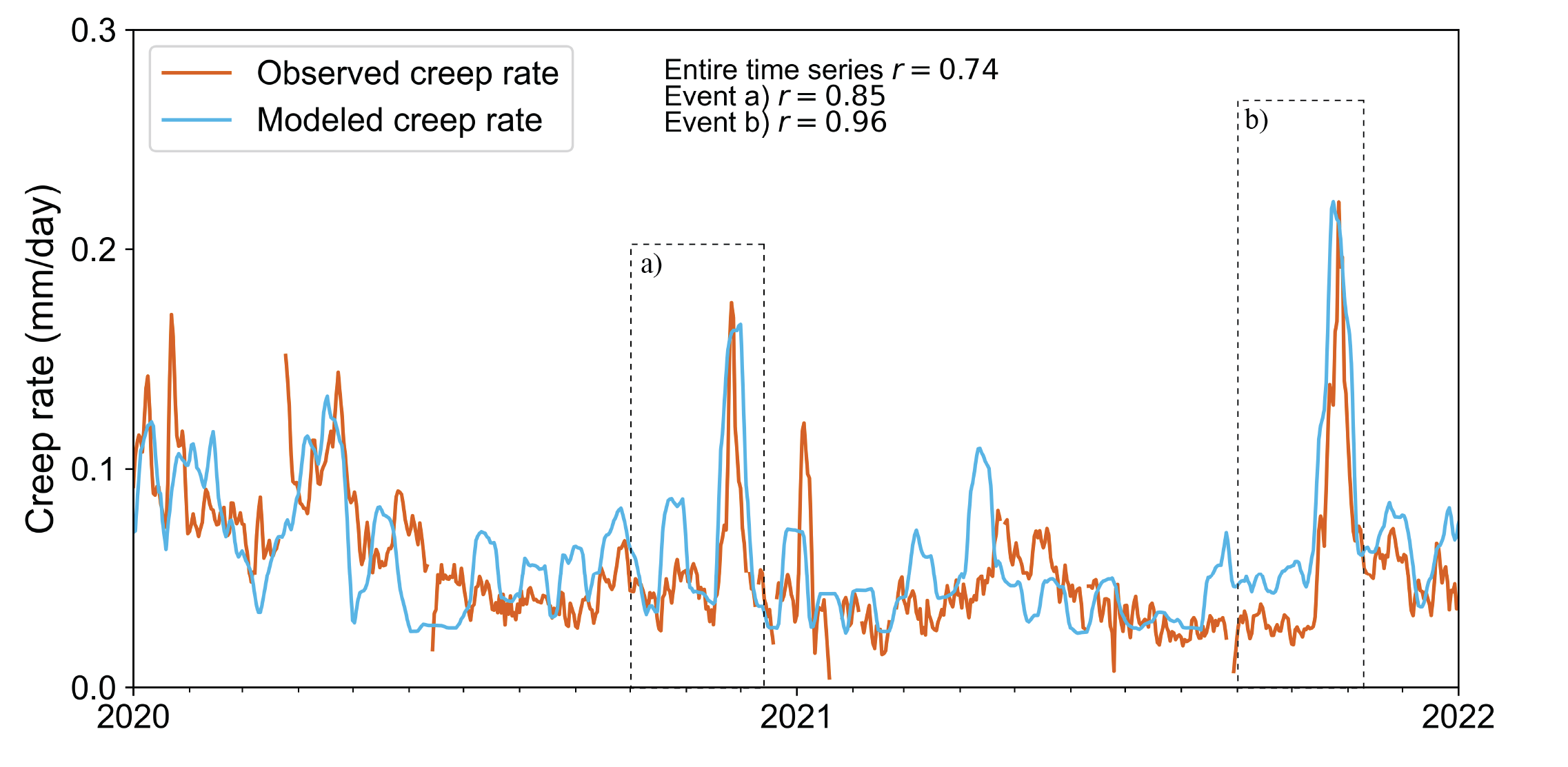
The forces caused by seepage through soil is well-established in engineering and is accounted in the design of geotechnical infrastructures, such as embankment dams and retaining walls. Seepage exerts a similar forcing in the deformation of landslides if much of the moving body is strained by macroscopic fluid flow [6,8,17]. However, the micromechanical effect of seepage and its coupling to the rheology, the stability and the creep dynamics of localized shear zone remains overlooked. In this work, we address the need for a generic analytical tool, describing the combined effects of seepage and fluid pore-pressure, in driving water-assisted landslide creep. This model may be used to predict landslide motion and improving landslide hazard mitigation. The predictive capacity of the proposed model is demonstrated by matching creep field data of the Åknes landslide in Norway and establishes how seepage forces operating only within the thin shear zone of a landslide can nonetheless exert a major control on seasonal creep bursts.
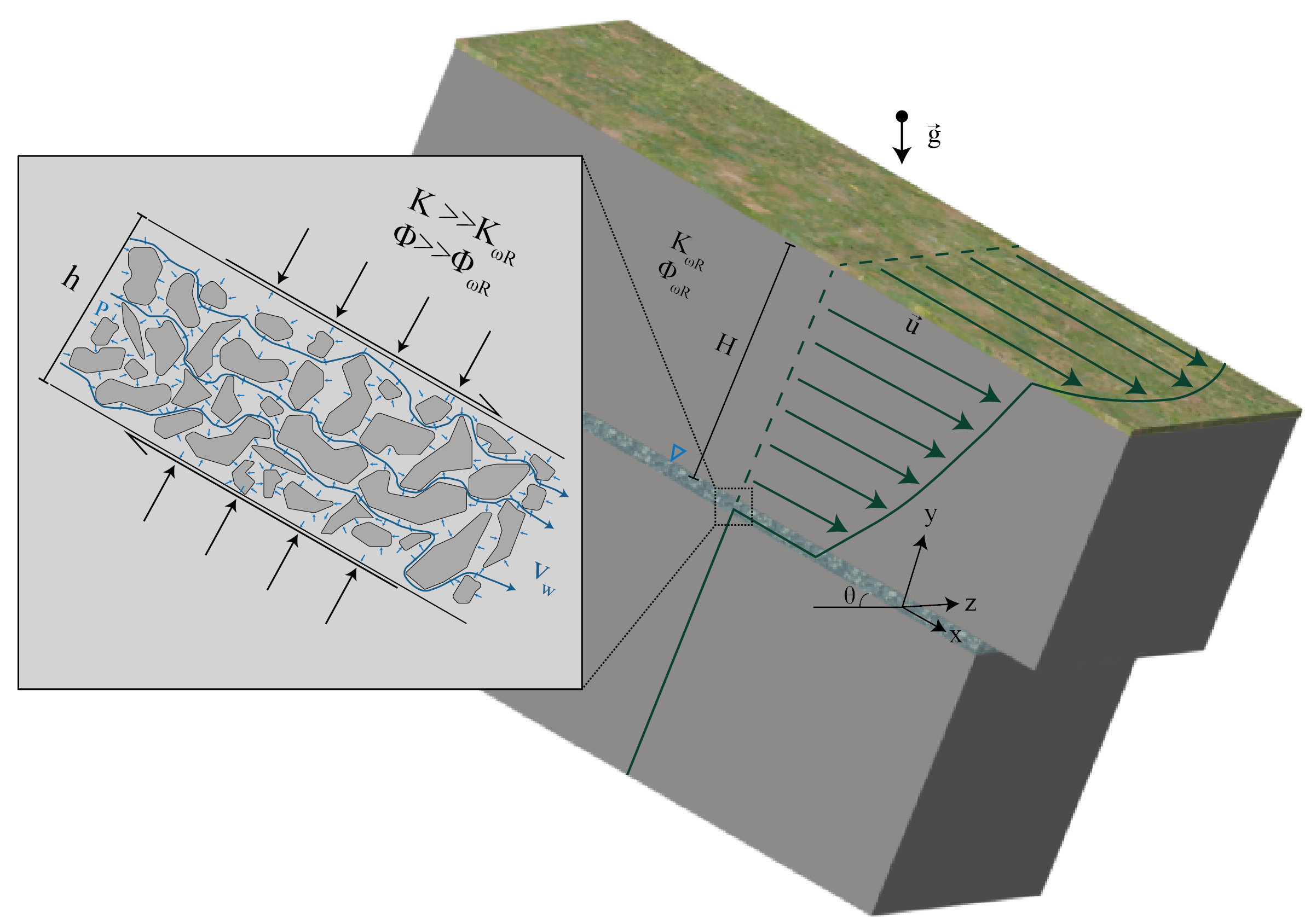
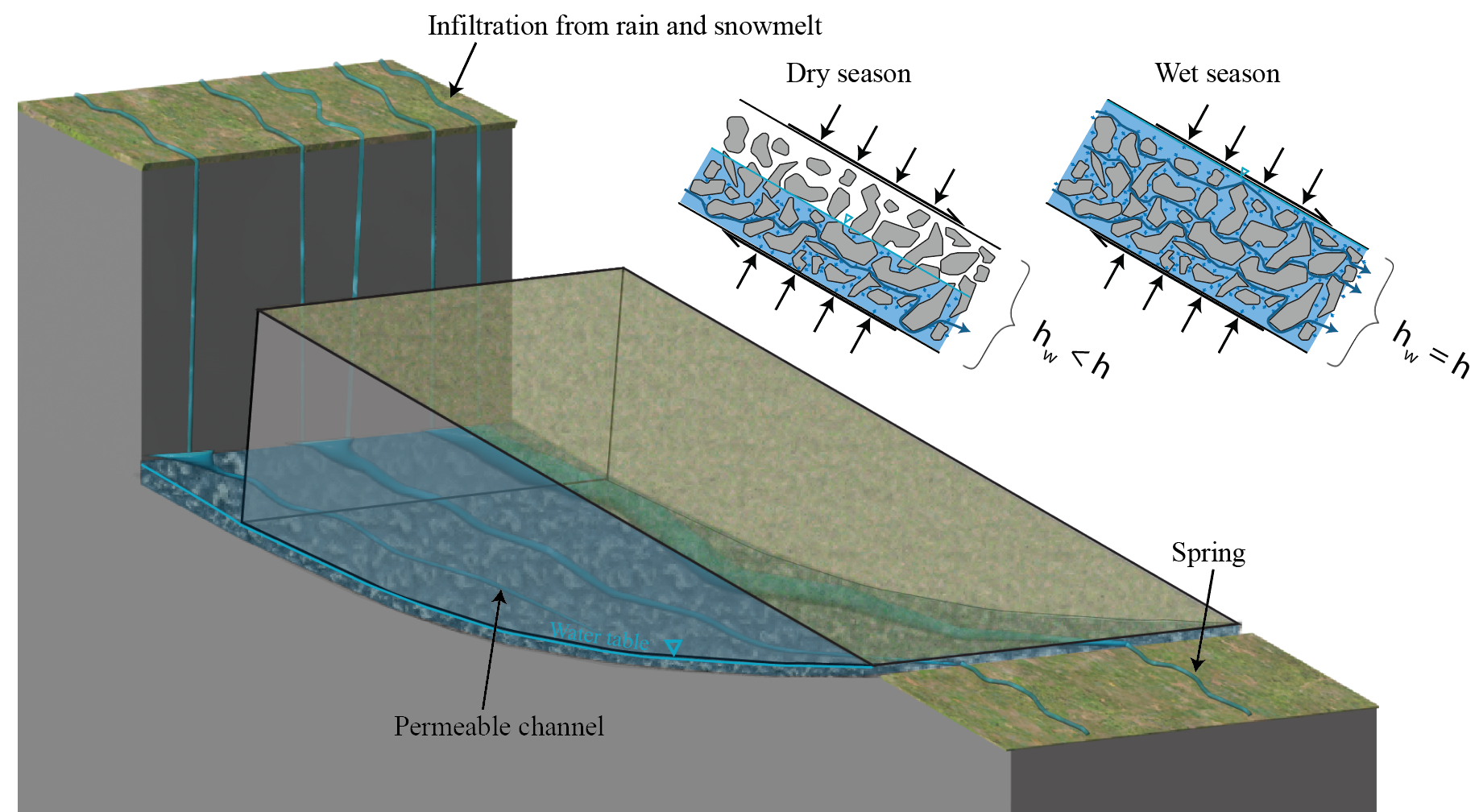
Fig. 1 Geometry of a typical creeping landslide studied in this work. A rock mass of thickness H slides downhill following a slip profile u where most of the strain is localised within a shear zone of thickness h made up of debris and rock particles crushed by frictional sliding. Due to its granular nature, the damaged shear zone has a larger porosity ϕ and hydraulic conductivity K than the surrounding competent rock mass (Kwr,ϕwr) and represents a favourable flow corridor for underground water. The inset details the effect of water at the grain scale of the shear zone, which is twofold: 1) a hydrostatic effect caused by the pore pressure p, which reduces the effective normal stress and 2) the seepage force exerted by fluid flowing at an average rate vw on the solid particles, which increases the shear stress at the base of the landslide.
We construct a generic mechanical model of creeping landslide. A rock mass of thickness H creeps down an inclined plane, with most of the shear strain localised into a shear zone of thickness h, leading to the profile of creep ⃗ u = u x ⃗ e x sketched in Figure 1. The deformation of the system is two-fold, since the creep rate ux = ∂u x /∂t results from the sum of elastic defo
This content is AI-processed based on open access ArXiv data.