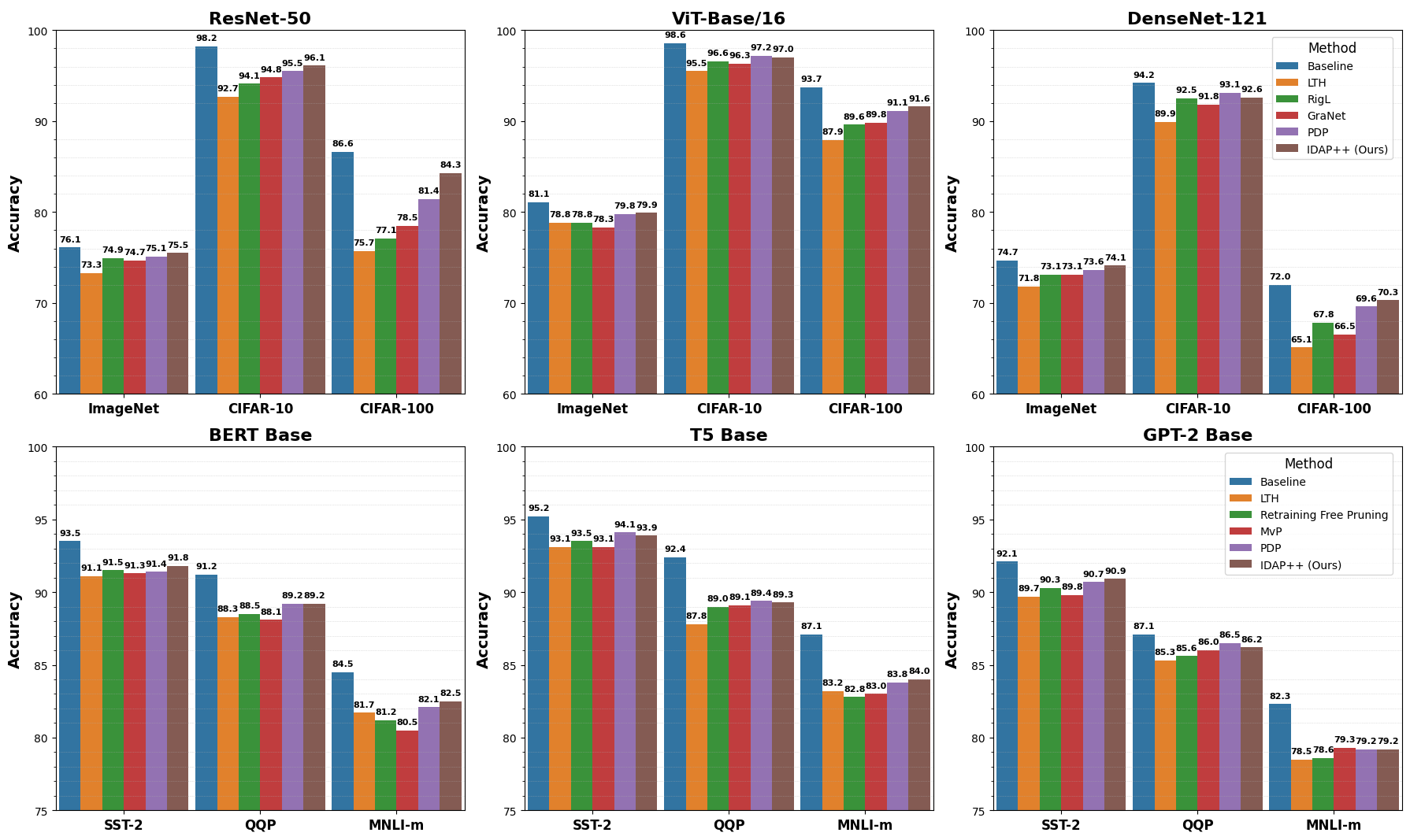
This paper presents a novel approach to neural network compression that addresses redundancy at both the filter and architectural levels through a unified framework grounded in information flow analysis. Building on the concept of tensor flow divergence, which quantifies how information is transformed across network layers, we develop a two-stage optimization process. The first stage employs iterative divergence-aware pruning to identify and remove redundant filters while preserving critical information pathways. The second stage extends this principle to higher-level architecture optimization by analyzing layer-wise contributions to information propagation and selectively eliminating entire layers that demonstrate minimal impact on network performance. The proposed method naturally adapts to diverse architectures, including convolutional networks, transformers, and hybrid designs, providing a consistent metric for comparing the structural importance across different layer types. Experimental validation across multiple modern architectures and datasets reveals that this combined approach achieves substantial model compression while maintaining competitive accuracy. The presented approach achieves parameter reduction results that are globally comparable to those of state-of-the-art solutions and outperforms them across a wide range of modern neural network architectures, from convolutional models to transformers. The results demonstrate how flow divergence serves as an effective guiding principle for both filter-level and layer-level optimization, offering practical benefits for deployment in resource-constrained environments.
The first stage targets filter-level optimization: divergence measurements (Dineen, 2014;Tran, 2018;Perrella et al., 2023;Lopes & Ruggiero, 2021;Kim et al., 2013;Machenhauer & Rasmussen, 1972;Rezende & Mohamed, 2016) prune redundant parameters while preserving critical pathways (Shwartz-Ziv, 2022;Saxe et al., 2018;Wu et al., 2022;Munezero et al., 2021;Yu et al., 2025;Greff et al., 2015). The second stage extends to layer-level compression, consolidating blocks based on their contribution to overall information throughput. Unlike traditional methods that focus only on parameter or layer counts, our framework jointly optimizes both while respecting information dynamics.
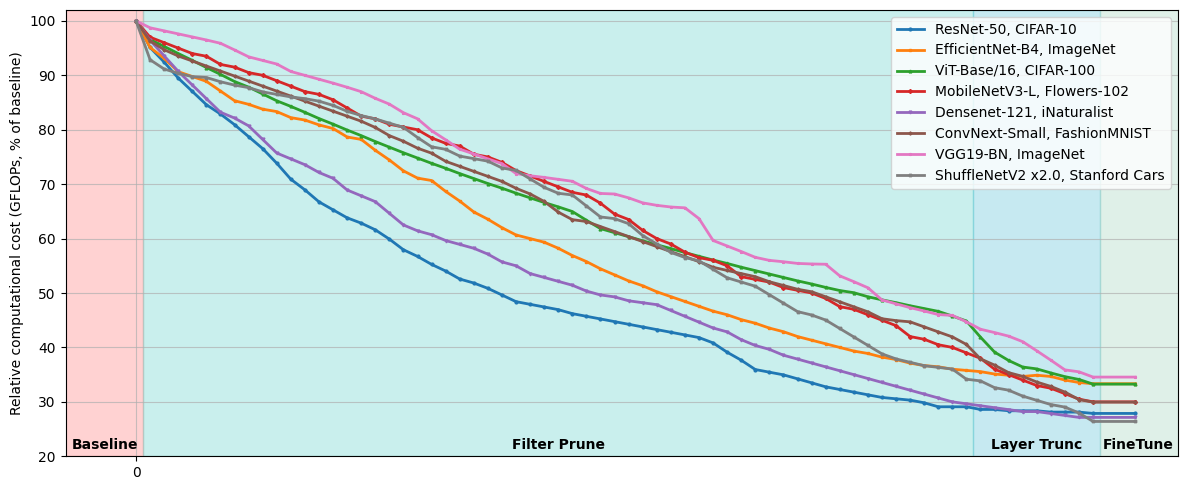
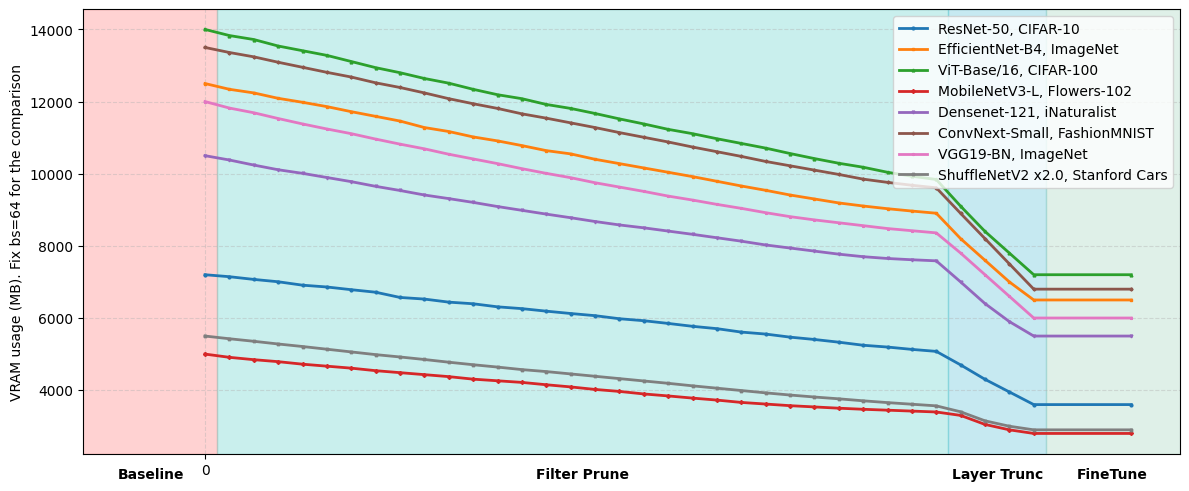
We provide algorithmic specifications for various layer types and demonstrate that this holistic approach outperforms isolated strategies. Experiments across convolutional and transformer architectures show substantial model size reductions without compromising functionality.
Ultimately, this framework is not only a compression tool but a new perspective on neural network design, where measurable information flow guides architectural decisions, enabling models that are smaller and computationally more efficient.
Thus, the main contributions of our work to neural network compression are as follows:
• Two-Stage Holistic Compression Framework. We propose the first pruning methodology that systematically optimizes neural networks along both width (filter-level) and depth (layer-level) dimensions through a unified flow-divergence criterion. The framework combines:
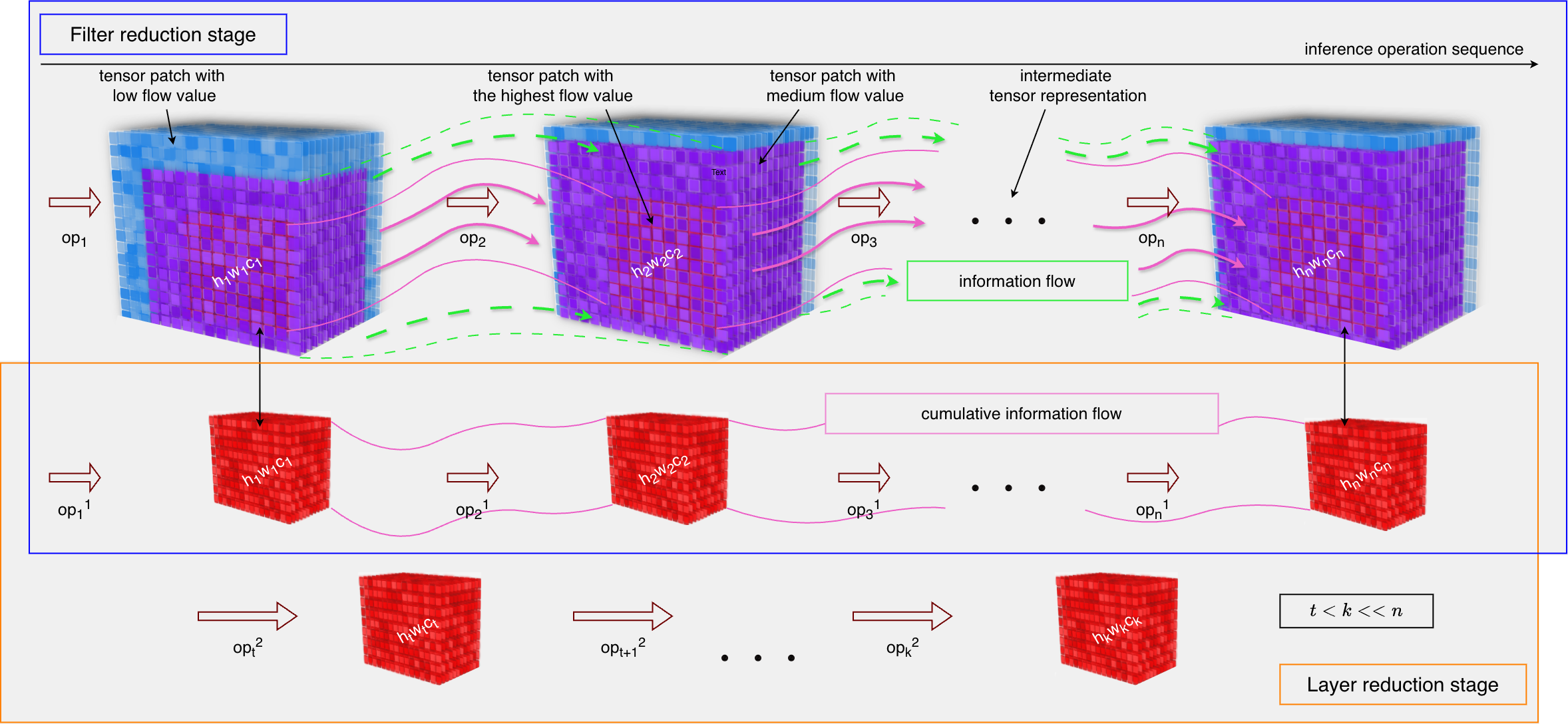
-Stage 1: Divergence-Aware Filter Pruning (IDAP).
-Stage 2: Flow-Guided Layer Truncation. • Theory of Information Flow Divergence. A mathematically rigorous formulation of neural network dynamics as continuous signal propagation systems, with:
-Integral-based divergence measures for discrete/continuous layers.
-Architecture-agnostic flow conservation principles.
These factors underscore the need for principled approaches that can reliably detect redundancy and optimize structures while accounting for internal information processes. In this work, we address this problem with a pruning framework grounded in information flow dynamics, which enables the safe removal of non-essential components.
3 PROPOSED SOLUTION
We present a comprehensive theoretical framework for analyzing information propagation through deep neural networks by modeling them as dynamical systems that transform input data through successive nonlinear transformations. The key insight is to characterize how information content evolves as it flows through the network’s computational path.
For a neural network f θ : X → Y with parameters θ, we represent its computations as a continuous trajectory:
• s = 0 corresponds to the input layer;
• s = 1 corresponds to the output layer;
• intermediate s values represent hidden transformations.
The differential change captures the instantaneous information flow:
This formulation offers several important advantages. First, it establishes a connection to dynamical systems theory, providing a solid mathematical foundation for analyzing information flow. Second, it enables a unified treatment of both discrete and continuous architectures. Finally, it naturally accommodates residual connections.
We define flow divergence to quantify information dissipation/concentration:
For practical computation in discrete networks with L layers:
where ϵ = 10 -6 prevents numerical instability. This approximation preserves derivative-based interpretation and remains computationally tractable. It also captures both magnitude and directional changes. It should be noted that Flow Divergence possesses the property of gradient stability (the proof of this is provided in Section J.1).
We also provide an extension of the flow divergence measure through variance-based normalization (see Section A.1), which improves interpretability and robustness compared to exponential normalization. Furthermore, we present a formal treatment of the key mathematical properties of the introduced divergence measure (see Section A.2), including scale invariance and additive composition.
Our flow divergence measure fundamentally differs from existing information-theoretic metrics. Unlike Fisher Information or global sensitivity measures operating in parameter space, our approach is intrinsically tied to the topological structure of information-propagation pathways. This architectural grounding enables unified optimization across both filter-level and layer-level compression within a single framework. Whereas conventional metrics assess general informativeness without providing automatic optimization criteria, our flow divergence naturally yields pruning directives by quantifying information evolution along computational trajectories. Crucially, our method requires no mathematical prerequisites beyond standard gradient-based learning -any gradient-trainable architecture can be analyzed using our measure. This repres
This content is AI-processed based on open access ArXiv data.