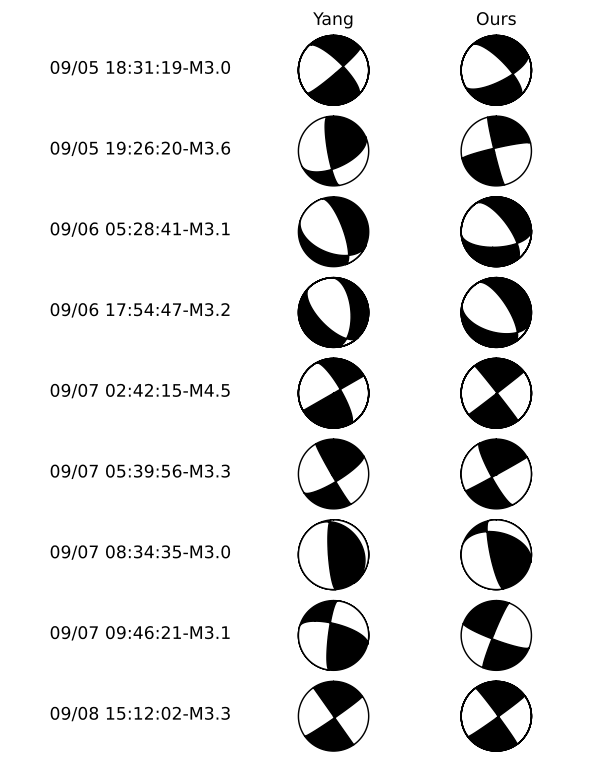
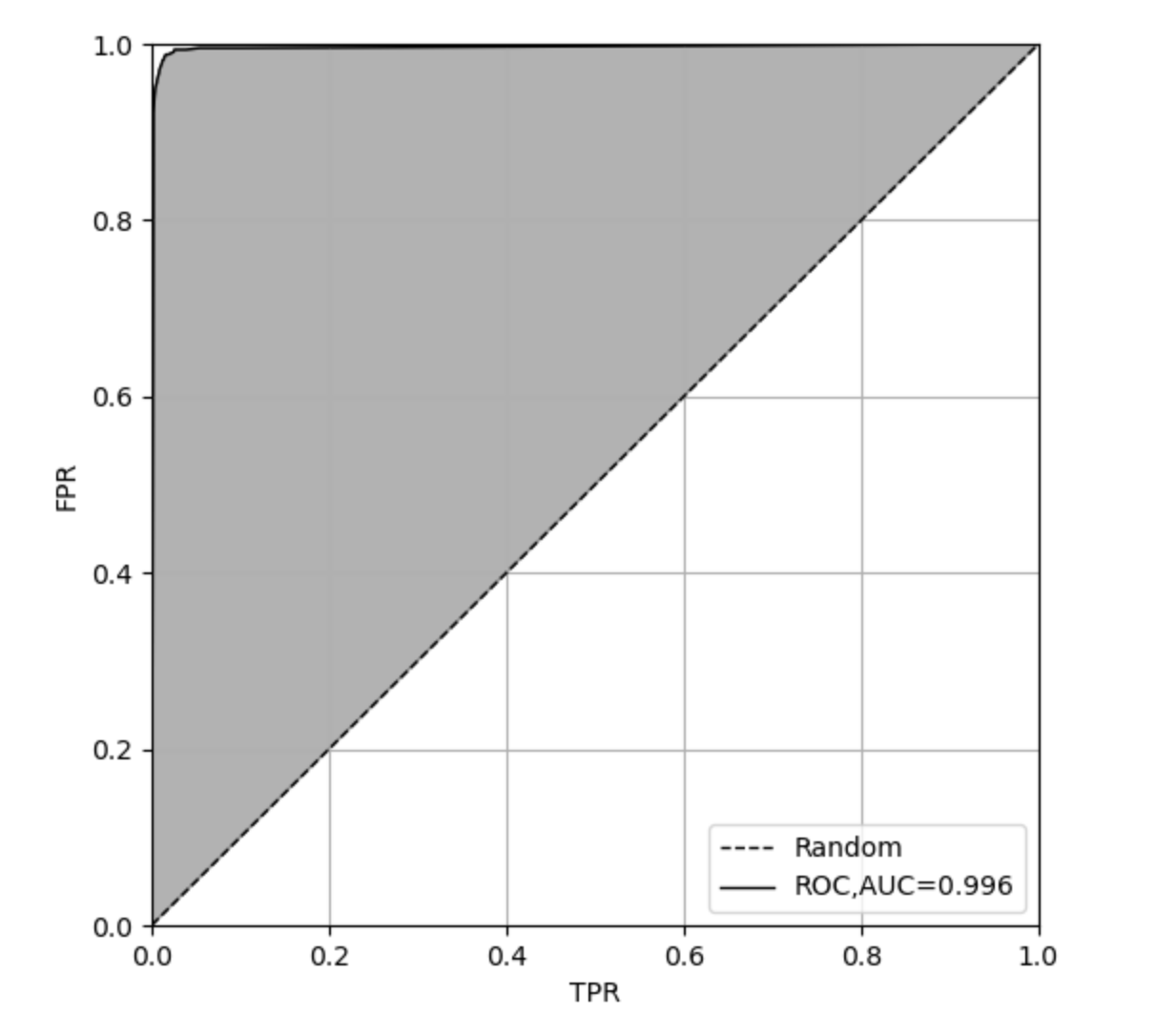
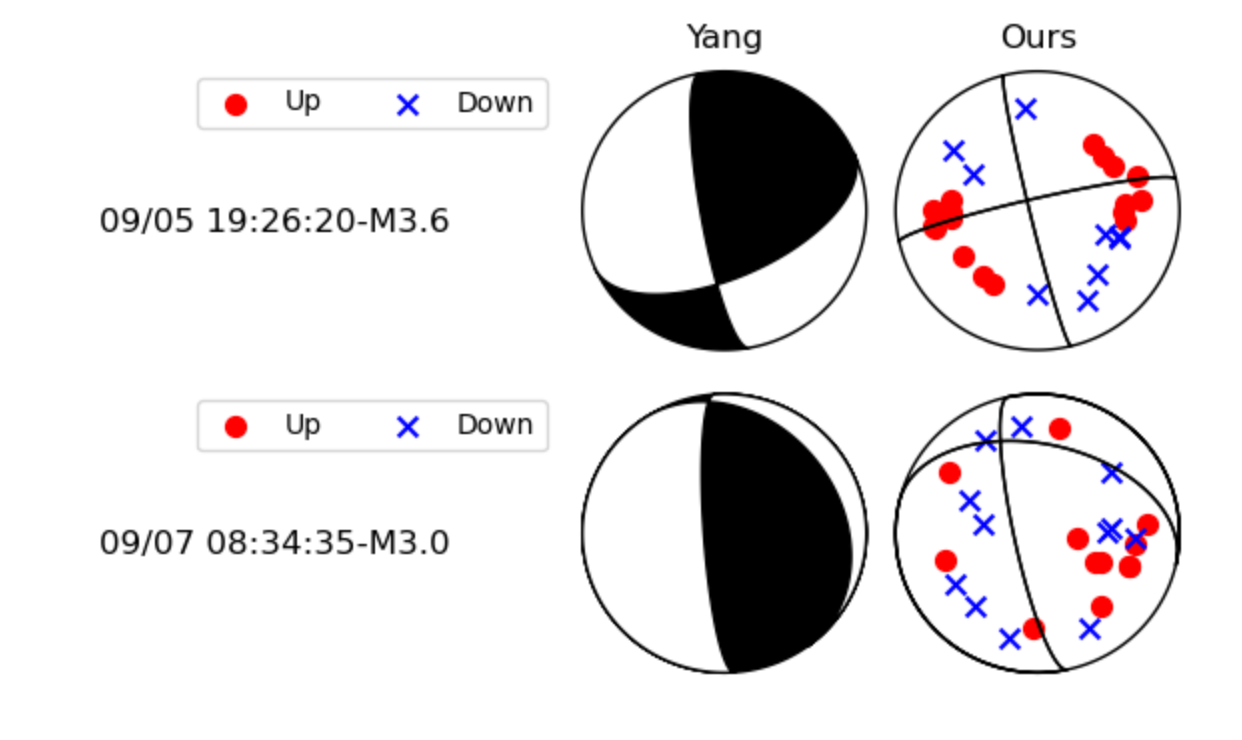
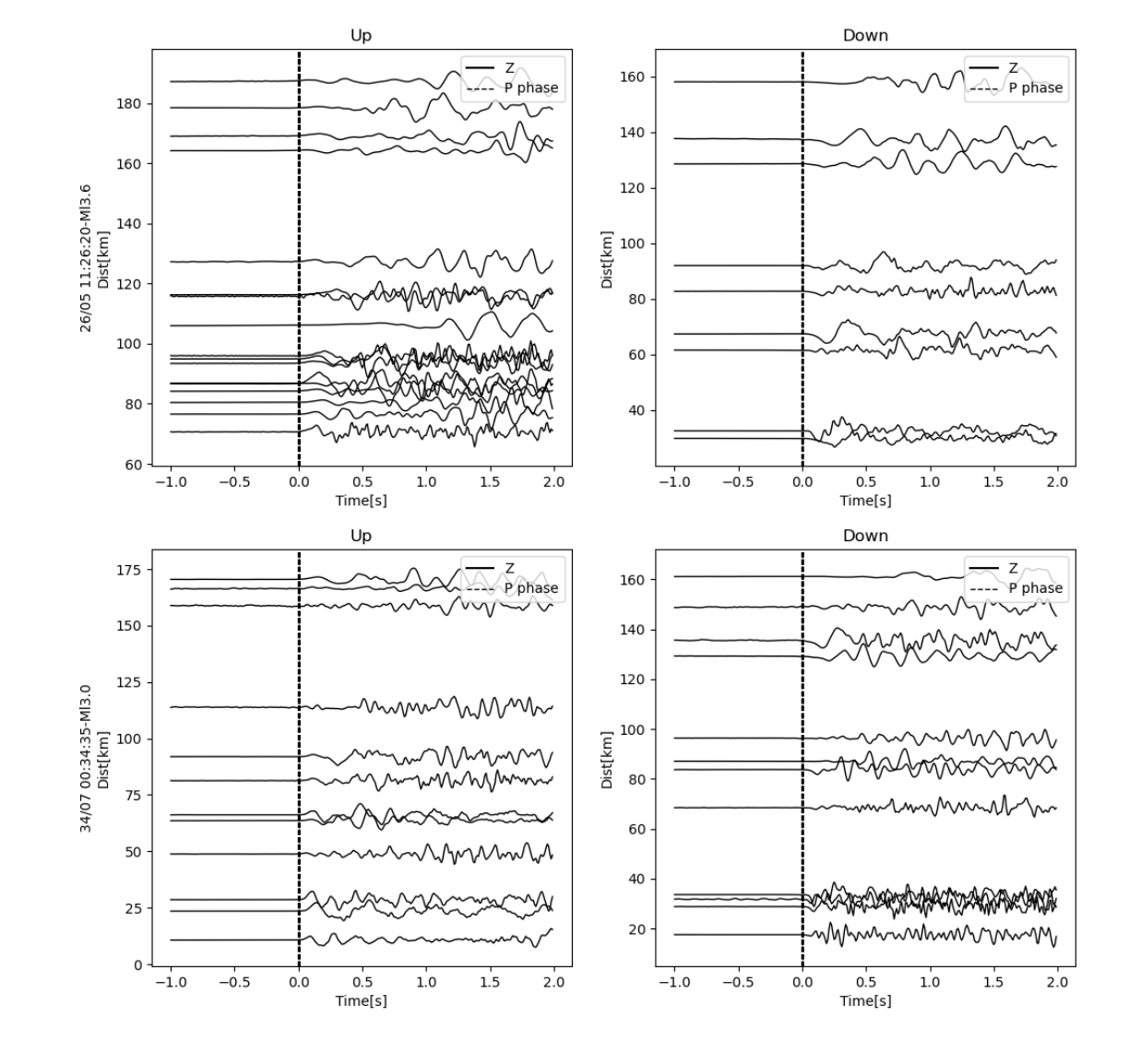
P-wave first-motion polarity plays an important role in resolving focal mechanisms of small to moderate earthquakes (M <= 4.5). High-quality focal mechanism solutions for abundant small events can greatly improve our understanding of regional tectonics, fault geometries, and stress-field characteristics. In this study, we develop an automated focal mechanism determination framework that integrates deep neural networks with P-wave first-motion polarity observations, and apply it to the 2022 Luding earthquake sequence. The model is trained on 12 years (2009-2020) of manually annotated 100 Hz waveform records from the China National Seismic Network, achieving a polarity recall of 97.4 percent and a precision of 98.5 percent. After automatically determining the first-motion polarities, we invert focal mechanisms using the HASH method. The resulting focal mechanism solutions show high consistency with mapped fault structures in the Luding region, demonstrating the reliability and applicability of the proposed workflow.
Focal mechanism solutions provide essential information on fault strike, dip, and rake angles, forming the basis for understanding regional stress fields, crustal deformation, tectonic structures, and seismic hazard assessment [1,2,3,4,5,6]. Small to moderate earthquakes (M ≤ 4.5) occur in large numbers and exhibit dense spatiotemporal distributions; they are sensitive to small-scale fault structures and stress perturbations. As a result, these events play an important role in investigating crustal dynamics [7] and assessing the likelihood of future large earthquakes [8,9,10,11].
Traditional methods for determining focal mechanisms can be broadly categorized into two groups. The first group comprises waveform-inversion approaches, which estimate source parameters by fitting synthetic waveforms to observed records. These methods are widely used for moderate-to-large earthquakes [12,13,14] and can produce stable results even in regions with sparse station coverage. However, waveform inversion requires accurate velocity models and high signal-to-noise ratios, and its effectiveness is limited for small events because their radiated energy is concentrated at higher frequencies [15,16]. For small earthquakes, the rupture duration is short and the source dimension is small, such that the events can often be approximated by double-couple sources [17,7]. Because the waveforms of small earthquakes are generally simple, focal mechanism solutions obtained from P-wave first-motion polarities are often consistent with those derived from waveform fitting [18,19]. P-wave first-motion polarity has clear physical meaning, does not strongly depend on velocity-model accuracy, and can be inverted through grid search, making it a robust observable for determining focal mechanisms. Methods such as FPFIT [20] invert focal mechanisms by fitting first-motion data mapped onto the focal sphere. However, uncertainties in velocity models and polarity picking introduce non-negligible errors [21]. To address these limitations, the HASH method [21,22] incorporates model perturbations and P/S amplitude ratios, resulting in more stable solutions. Previous studies have shown that well-distributed stations and reliable polarity readings substantially improve focal mechanism accuracy [23]. Conversely, for small near-source events, velocity-model uncertainty can greatly affect takeoff-angle calculations and degrade solution quality [24]. To mitigate uneven station coverage, probabilistic approaches and grid-based spatial parameterization have also been proposed [25].
With the deployment of dense seismic networks, large volumes of high-quality waveform data have become available. However, manual annotation of first-motion polarities is labor-intensive, motivating the development of automated polarity classifiers. Traditional automatic approaches, such as zero-crossing counts [26] and Bayesian algorithms [27], rely on hand-crafted features and are sensitive to phase-picking accuracy. In contrast, data-driven deep learning methods have demonstrated exceptional performance in computer vision and natural language processing, and have been increasingly applied in seismology, including phase picking [28,29], focal mechanism estimation [30], and earthquake classification [31]. Several studies have confirmed the effectiveness of neural networks for P-wave polarity determination [32,33,16,18].
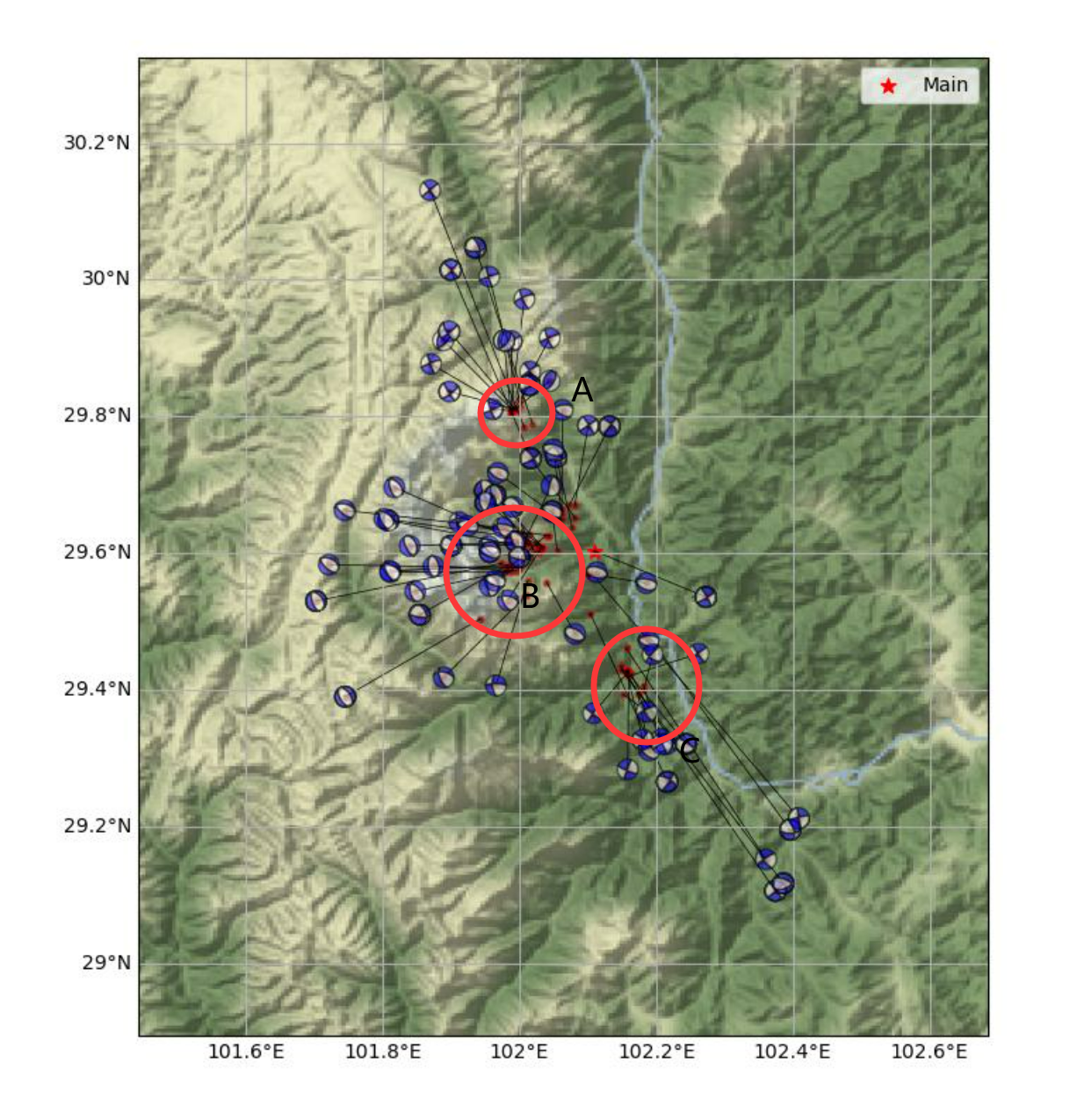
To efficiently compute focal mechanisms for small to moderate earthquakes (M ≤ 4.5) recorded by dense seismic arrays, we develop an automated focal mechanism determination framework based on P-wave first-motion polarity. We employ a recurrent-neural-network-based phase picker for accurate arrival-time estimation [28], and design a multi-layer residual network for polarity classification. The model is trained using 11 years (2009-2019) of manually labeled data from the China National Seismic Network (CSN) and evaluated on independent manually annotated data from 2020. Tests show that the trained model achieves performance comparable to manual classifications, and remains robust even when the P-wave pick contains timing errors. Finally, we invert focal mechanisms using the HASH grid-search algorithm [21]. Based on the Luding earthquake sequence catalog of [34], we compute focal mechanisms and compare them with waveform-based solutions reported by [7].
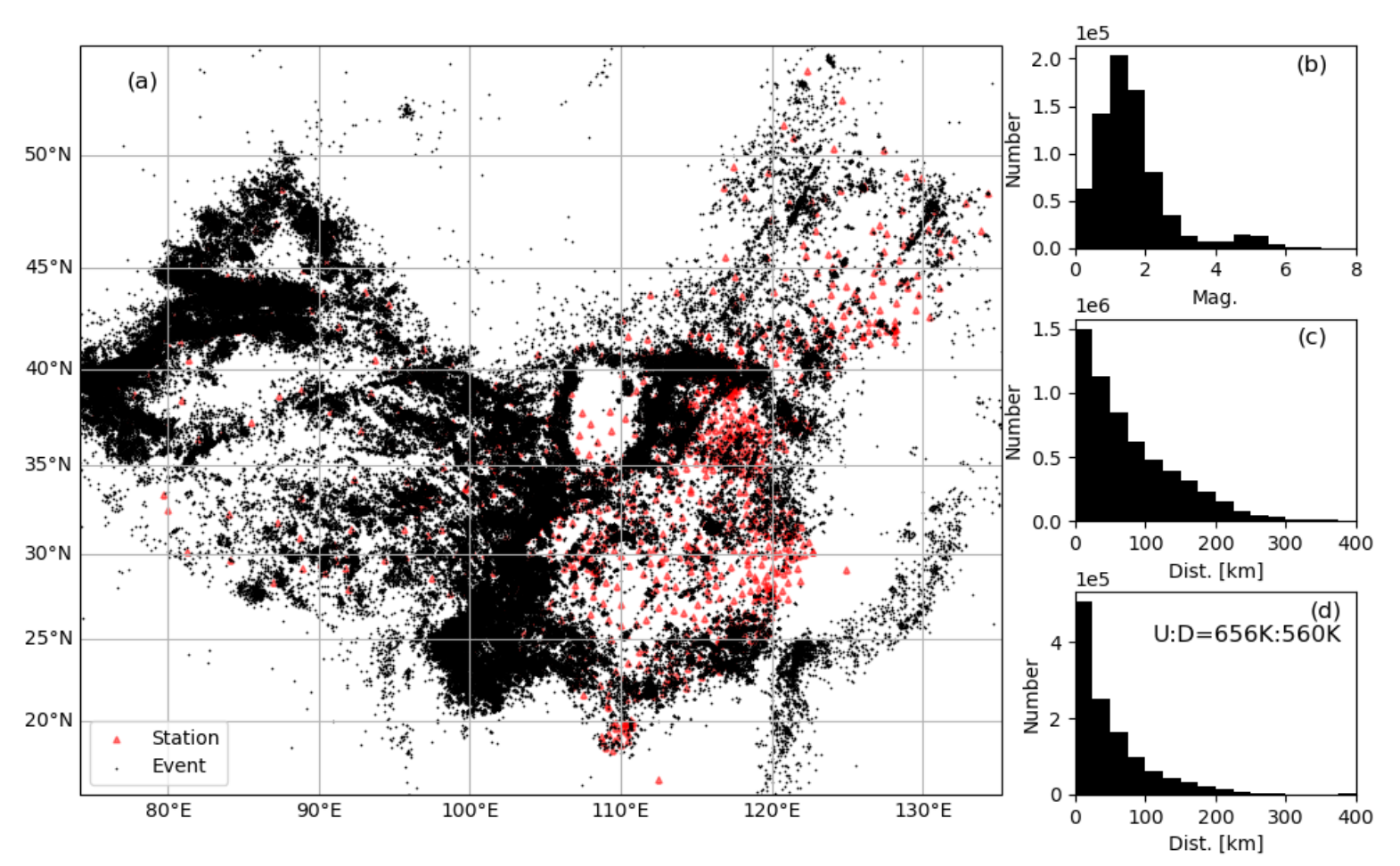
2 Methods and Data As shown in Figure 1a, the combined distribution of earthquakes and stations ensures comprehensive coverage across mainland China, enabling the model to generalize well within this region. The proportions of upward and downward firstmotion polarities are nearly balanced (approximately 1:1; Figure 1d), and therefore additional sampling re-balancing is unnecessary.
To evaluate the polarity-detection performance, we divide the dataset into training and testing subsets. Data from 2009-2019 serve as the training set, while data from 2020 serve as the independent test set. The test dataset includes 82,
This content is AI-processed based on open access ArXiv data.