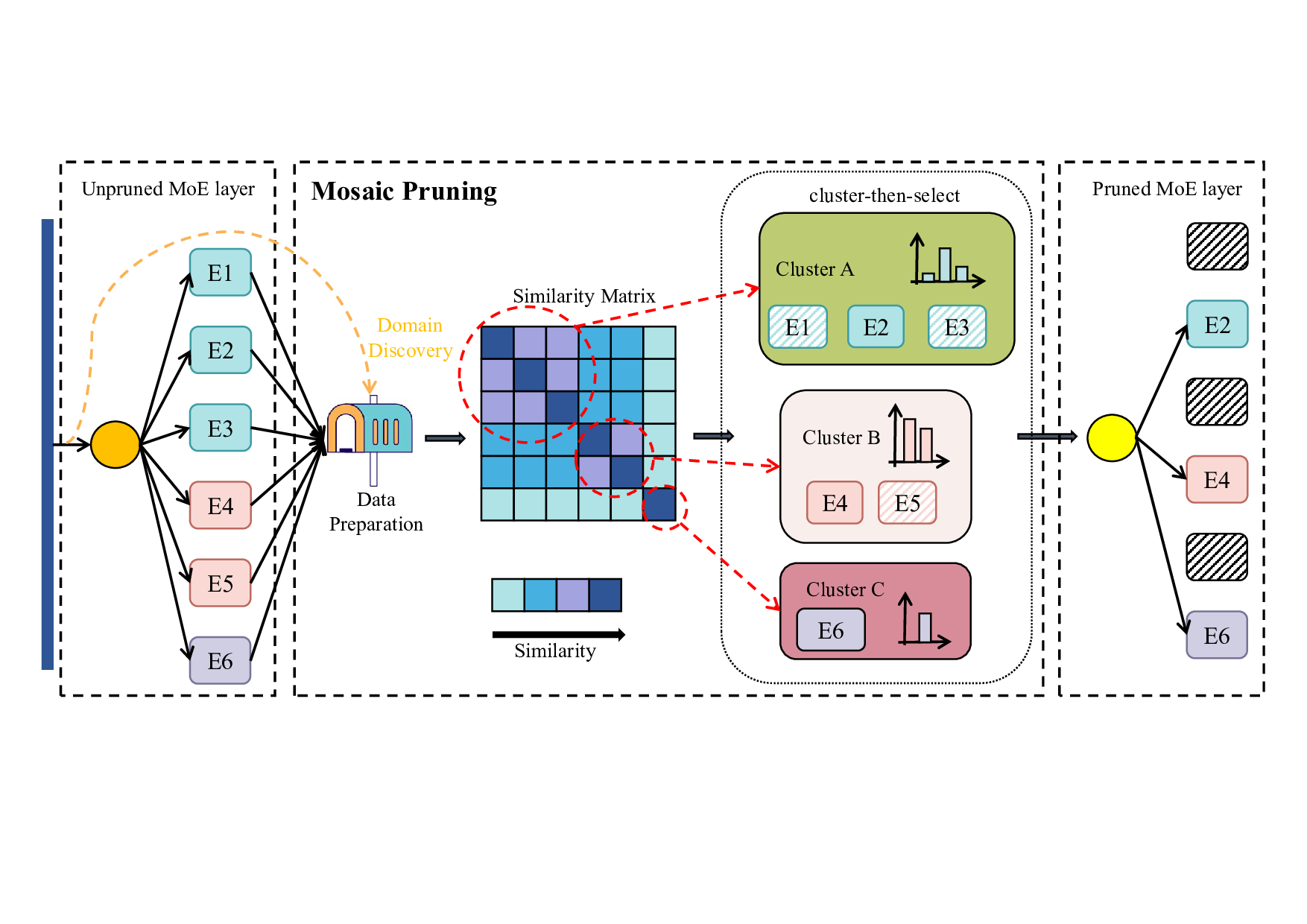
Sparse Mixture-of-Experts (SMoE) architectures have enabled a new frontier in scaling Large Language Models (LLMs), offering superior performance by activating only a fraction of their total parameters during inference. However, their practical deployment is severely hampered by substantial static memory overhead, as all experts must be loaded into memory. Existing post-training pruning methods, while reducing model size, often derive their pruning criteria from a single, general-purpose corpus. This leads to a critical limitation: a catastrophic performance degradation when the pruned model is applied to other domains, necessitating a costly re-pruning for each new domain. To address this generalization gap, we introduce Mosaic Pruning (MoP). The core idea of MoP is to construct a functionally comprehensive set of experts through a structured ``cluster-then-select" process. This process leverages a similarity metric that captures expert performance across different task domains to functionally cluster the experts, and subsequently selects the most representative expert from each cluster based on our proposed Activation Variability Score. Unlike methods that optimize for a single corpus, our proposed Mosaic Pruning ensures that the pruned model retains a functionally complementary set of experts, much like the tiles of a mosaic that together form a complete picture of the original model's capabilities, enabling it to handle diverse downstream tasks.Extensive experiments on various MoE models demonstrate the superiority of our approach. MoP significantly outperforms prior work, achieving a 7.24\% gain on general tasks and 8.92\% on specialized tasks like math reasoning and code generation.
Large Language Models (LLMs) have recently demonstrated remarkable capabilities in complex reasoning and generation tasks (OpenAI 2024; Touvron et al. 2023b;Xiong et al. 2024). To mitigate their computational requirements, the Mixture-of-Experts (MoE) architecture has been widely adopted (Jiang et al. 2024). MoE models, such as Mixtral 8x7B, activate only a portion of their parameters during inference, enabling them to surpass the performance of larger dense models like Llama 2 70B while maintaining a smaller count of active parameters (Jiang et al. 2024;Touvron et al. 2023b).
Despite this efficiency, MoE models are constrained by a critical deployment challenge: immense static memory overhead. For instance, deploying Mixtral 8x7B requires over 80GB of GPU memory (Jiang et al. 2024). More importantly, due to training dynamics and representation learning differences, significant redundancy exists among experts in MoE models (Chi et al. 2022;Yu et al. 2022), with some experts being functionally similar or contributing minimally to most tasks.
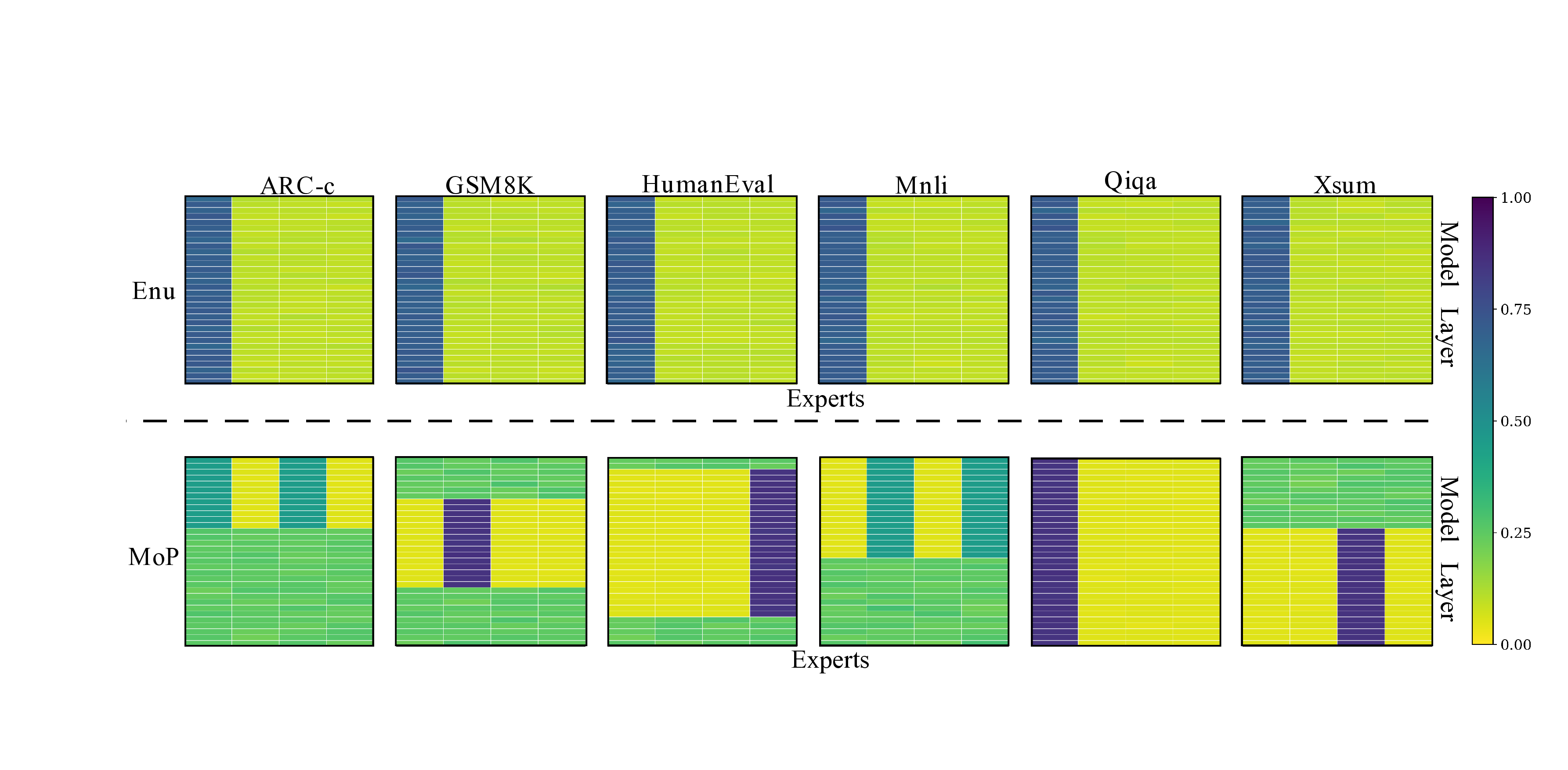
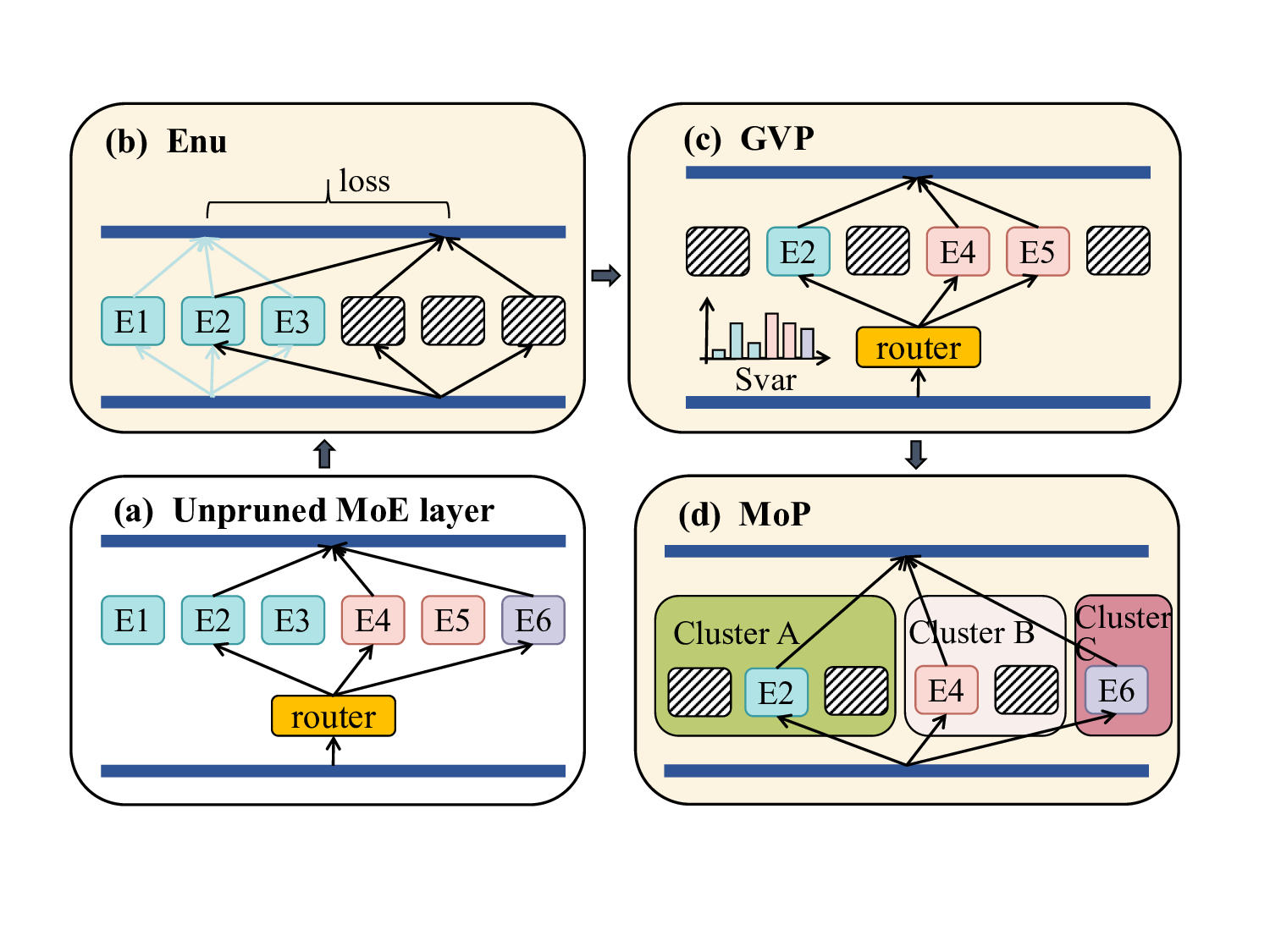
Leveraging the similarity between experts, post-training pruning has emerged as a promising approach for compressing MoE models. The state-of-the-art pruning method, Enumeration Pruning (Lu et al. 2024), utilizes a general-purpose calibration dataset (e.g., C4 and WikiText) to identify and remove experts that contribute least to token reconstruction loss. However, this method reveals a critical limitation: the inability to generalize to specialized downstream tasks. A model pruned on a general-purpose corpus suffers a catastrophic performance drop when directly applied to domainspecific tasks such as mathematical reasoning or code generation, a phenomenon we term functional collapse. We argue that this collapse occurs because such methods inherently favor retaining generalist experts that make moderate contributions across common data patterns, while discarding specialist experts that possess critical domain-specific expertise but exhibit less prominent activation on general datasets. This necessitates re-pruning with a new calibration dataset for each new domain, a process that is not only impractical but also fundamentally undermines the model’s applicability. Given that different experts in MoE specialize in distinct knowledge domains, we argue that a model’s generalization capability fundamentally depends on the breadth of its functional diversity.
To address these challenges, we first propose a pruning strategy that actively preserves expert diversity,which we term Global Variability-aware Pruning (GVP). This method calculates an Activation Variability Score (S var ), constructed based on the Kullback-Leibler (KL) divergence (Kullback and Leibler 1951), for each expert and prioritizes retaining those with the highest scores. While our experiments confirm that GVP is superior to Enumeration Pruning, relying solely on the Activation Variability Score (S var ) may lead to the retention of two functionally similar experts that both possess high diversity scores, which still results in redundancy among the experts. To overcome this limitation, we propose a hierarchical pruning framework aimed at preserving functional diversity,which we call Mosaic Pruning (MoP). Our core idea is twofold: first, we use a composite metric, primarily driven by a Task Performance Similarity matrix (S perf ) (Spearman 1987), to assess functional similarity by analyzing expert performance across different task domains; second, within each functionally defined group, we select the most critical representative based on the Activation Variability Score proposed in GVP. This strategy ensures that no essential functional expertise is entirely eliminated, thus providing a strong inductive bias toward generalization across diverse tasks. Our extensive experiments on models such as Mixtral-8x7B (Jiang et al. 2024) and Qwen1.5-MoE-A2.7B (Yang et al. 2024) demonstrate the superiority of our method.
Our contributions are summarized as follows:
• We propose a novel diversity metric, the Activation Variability Score, to effectively identify experts with specialized functionalities. • We introduce a novel pruning framework that first groups experts based on their task performance similarity, and then prunes within each group to select a functionally complementary set of specialists based on our diversity metric. • We validate the superiority of our proposed method through extensive experiments, achieving an average performance improvement of 7.24% on general tasks, and a more significant 8.92% on specialized tasks such as mathematical reasoning and code generation.
The Mixture-of-Experts (MoE) paradigm, first introduced by (Jacobs et al. 1991), involves a collection of distinct subnetworks, or “experts,” coordinated by a trainable gating network that selectively routes inputs. This modular architecture was successfully integrated into modern deep learning with its application to Recurrent Neural Netwo
This content is AI-processed based on open access ArXiv data.