The Monte Carlo-type Neural Operator (MCNO) introduces a lightweight architecture for learning solution operators for parametric PDEs by directly approximating the kernel integral using a Monte Carlo approach. Unlike Fourier Neural Operators, MCNO makes no spectral or translation-invariance assumptions. The kernel is represented as a learnable tensor over a fixed set of randomly sampled points. This design enables generalization across multiple grid resolutions without relying on fixed global basis functions or repeated sampling during training. Experiments on standard 1D PDE benchmarks show that MCNO achieves competitive accuracy with low computational cost, providing a simple and practical alternative to spectral and graph-based neural operators.
Neural operators extend the success of neural networks from finite-dimensional vector mappings to infinite-dimensional function spaces, enabling the approximation of solution operators for partial differential equations (PDEs). These models learn mappings from problem inputs, such as coefficients or boundary conditions, to PDE solutions, allowing rapid inference and generalization across parameterized problem families. Early architectures like DeepONet [6] use branch and trunk networks, while Fourier Neural Operators (FNO) [5] leverage spectral convolutions and FFTs for efficient operator approximation on uniform grids. Wavelet-based models such as MWT [1] and WNO [7] improve spatial localization, and graph-based approaches like GNO [4] extend operator learning to irregular domains.
We propose the Monte Carlo-type Neural Operator (MCNO), a lightweight architecture that approximates the integral kernel of a PDE solution operator via Monte Carlo sampling, requiring only a single random sample at the beginning of training. By avoiding spectral transforms and deep hierarchical architectures, MCNO offers a simple yet efficient alternative that balances accuracy and computational cost. We evaluate MCNO on standard 1D PDEs, including Burgers’ and Korteweg-de Vries equations, using benchmark datasets, and show competitive performance against existing neural operators while maintaining architectural simplicity. Our contributions include the MCNO design, feature mixing for spatial and cross-channel dependencies, an interpolation mechanism for structured grids and benchmark evaluation.
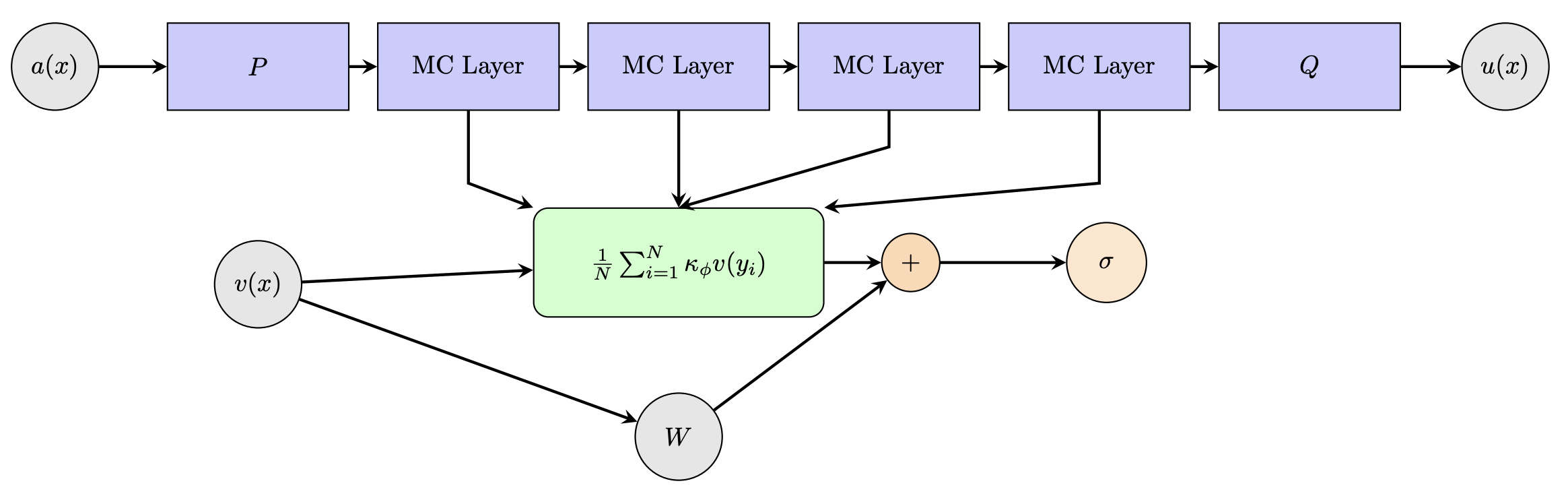
Neural operators provide a framework for learning mappings between infinite-dimensional function spaces, enabling efficient approximation of solution operators for parametric PDEs [2]. For a generic PDE, the true solution operator G † is a mapping that takes an input a to the corresponding PDE solution u s.t G † : a → u = G † (a). For many inputs, evaluating G † with classical solvers can be prohibitively expensive. Given a dataset {(a j , u j )} N j=1 with u j = G † (a j ), the goal is to learn a parameterized approximation G θ ≈ G † by minimizing a suitable loss. A neural operator adopts iterative architectures to compute such approximate operator G θ , to this end it lifts the input to a higher-dimensional representation v 0 (x) = P a(x) , x ∈ D ⊂ R d via a local map P . It then, updates it through a linear transformation via matrix W and a kernel-integral transformation (K ϕ v)(x) with nonlinear activations σ. The (t + 1)th, t ∈ N, neural operator layer is expressed as:
where κ ϕ is a learned kernel inspired by the Green function commonly involved in the solution of linear PDEs. A final projection Q maps the final features back to the target function space
MCNO follows this framework but replaces the integral with a Monte Carlo estimate over a fixed set of sampled points, i.e.,
This avoids spectral transforms or hierarchical architectures and achieves linear complexity in the number of sampled points. To enhance efficiency, MCNO leverages PyTorch’s einsum to perform the per-sample feature mixing in parallel by evaluating the kernel as
where each ϕ i ∈ R dv×dv is a learnable tensor acting on the feature vector v t (y i ) ∈ R dv , and we write ϕ = {ϕ i } N i=1 for the full set of kernel parameters. This design enables efficient GPU parallelization and avoids costly per-sample matrix operations before the Monte Carlo aggregation step. The Monte Carlo-type Neural Operator (MCNO) achieves linear computational complexity with respect to the number of samples N , since kernel interactions are computed only at the sampled points.
Because the Monte Carlo integral is evaluated on a subset of points, the resulting latent representation is interpolated to the full grid using lightweight linear interpolation, preserving efficiency while producing a structured output compatible with standard neural architectures. Although applied across the full grid, our reconstruction step scales linearly with N grid and involves only inexpensive local averaging, introducing only modest overhead compared to the kernel evaluation.
3 Bias-Variance Analysis and Dimensional Scaling At each layer, MCNO computes the kernel aggregation (1) using N points {y si } N i=1 sampled uniformly from the grid
In practice, tensor contractions parallelized over x give aggregation O(N ), while interpolation/reconstruction scales with N grid .
Error decomposition. Define
Variance. For fixed x, ( KN,
By a union bound over {x j } Ngrid j=1 and failure δ,
Sample complexity and cost. From ( 2)-( 3),
To reach tolerance ε, choose
with Õ hiding logarithms.
High-dimensional note. Dimension d enters via the bias (through N -1/d grid ) and grid cost; the Monte Carlo variance, and thus the stochastic sample complexity, remains dimension-independent.
We evaluate the Monte Carlo-type Neural Operator on two standard benchmark problems: Burgers’ equation and Korteweg-de Vries (Kd
This content is AI-processed based on open access ArXiv data.