Approximating training-point influence on test predictions is critical for deploying deep-learning vision models, essential for locating noisy data. Though the influence function was proposed for attributing how infinitesimal up-weighting or removal of individual training examples affects model outputs, its implementation is still challenging in deep-learning vision models: inverse-curvature computations are expensive, and training non-stationarity invalidates static approximations. Prior works use iterative solvers and low-rank surrogates to reduce cost, but offline computation lags behind training dynamics, and missing confidence calibration yields fragile rankings that misidentify critical examples. To address these challenges, we introduce a Stability-Guided Online Influence Framework (SG-OIF), the first framework that treats algorithmic stability as a real-time controller, which (i) maintains lightweight anchor IHVPs via stochastic Richardson and preconditioned Neumann; (ii) proposes modular curvature backends to modulate per-example influence scores using stability-guided residual thresholds, anomaly gating, and confidence. Experimental results show that SG-OIF achieves SOTA (State-Of-The-Art) on noise-label and out-of-distribution detection tasks across multiple datasets with various corruption. Notably, our approach achieves 91.1\% accuracy in the top 1\% prediction samples on the CIFAR-10 (20\% asym), and gets 99.8\% AUPR score on MNIST, effectively demonstrating that this framework is a practical controller for online influence estimation.
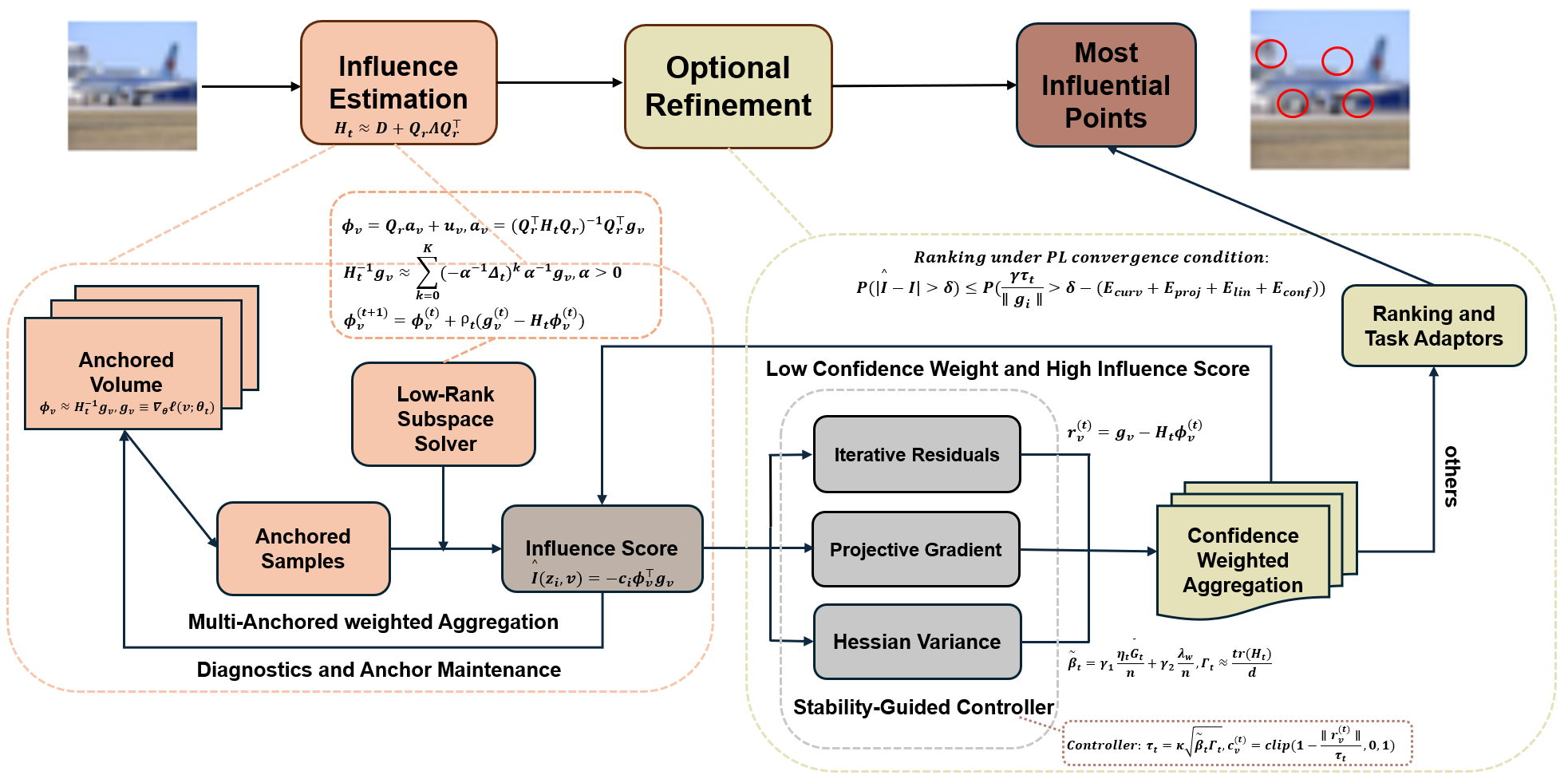
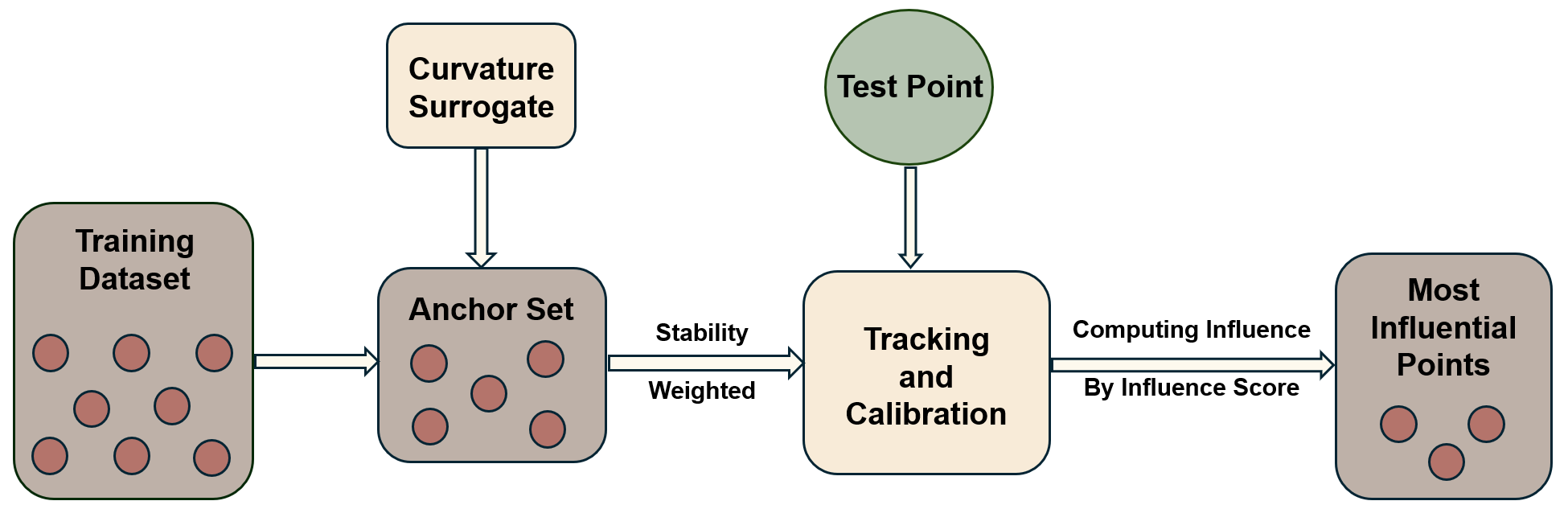
Modern vision systems are increasingly deployed in highstakes, compliance-sensitive settings [19,58], where accountability must extend beyond aggregate accuracy to continuous, per-example oversight-surfacing mislabeled or lowquality samples [48], detecting distribution shift [43,52], resisting data poisoning [62] and enabling selective unlearning [8,24]. Regulatory and operational requirements, such as the right to erasure and continual risk assessments [55] further demand streaming influence assessment rather than sporadic offline diagnostics. Workflow is shown in Fig. 1 Figure 1. Workflow of SG-OIF. The vature surrogate for the surrogate is updated online; then inverse Hessian vector proxies for anchors are tracked with lightweight iterations and calibrated by stability-based confidence; the influence of training data points is computed by aggregating stability-weighted per-anchor scores, with optional refinement when high-influence but low-confidence; finally, the most influential training data points are returned.
Influence functions originate in robust statistics, quantifying the infinitesimal effect of perturbing one observation on an estimator [13,15,26,32,50]. However, deploying influence estimation in modern deep vision models is challenging because it hinges on inverse-curvature computations that are expensive, ill-conditioned, and misaligned with the nonstationary dynamics of training. Koh and Liang [34] adapted them to modern ML by approximating inverse Hessian-vector products with iterative second-order methods, enabling per-example attributions in high dimensions. However, this route inherits notable limitations in deep networks: Offline curvature quickly becomes stale along the training trajectory, and iterative Inverse Hessian Vector Product (IHVP) solvers are numerically fragile under non-convex saddle geometry. Further studies [36] evaluate offline settings on convex and near-convex surrogates, but they also face limitations: Without calibrated confidence, there is little guidance for anomaly gating in nonconvex deep networks.
Algorithmic stability provides a complementary lens for generalization aligned with governance. In regularized ERM [34], if replacing one point changes the loss by at most a small stability coefficient β n , generalization scales with this coefficient; for strongly convex [36], Lipschitz losses with Tikhonov regularization, this coefficient becomes tighter as regularization strengthens and the sample size grows. Extensions to iterative procedures analyze SGD perturbations across neighboring datasets, with β n controlled by cumulative step sizes and smoothness; in nonconvex settings, multiplicative smoothness inflates β n . Robust training further stresses stability, as nonsmooth [39], weakly convex objectives can make vanilla adversarial SGD non-uniformly stable, aligning with robust overfitting; smoothing and proximal designs [66] can help recover stability guarantees on the order typical of well-regularized regimes. Thus, the field evolves from convex ERM with explicit formulas, through stepwise analyses of stochastic optimization, to a stable restoring and shifting design principle.
Across governance tasks, the core need is to rank training examples by causal leverage with calibrated reliability. Existing tools face multiple challenges. Shapley-style valuation [47] is combinatorial and high-variance, straining budgets in large-scale settings-motivating lighter surrogates with variance control. Classical influence [1,5,20] is based on inverse curvature; IHVP pipelines are fragile in saddlerich non-convex regimes, motivating curvature-aware updates with online refresh and stability gating. Trajectory heuristics [34] entangle optimization transients with causality, mis-ranking late-stage hard cases-calling for drift-aware corrections and temporal consistency. Classical stability [72] provides dataset-level worst-case bounds without perexample confidence-necessitating calibrated, instance-level confidence to gate large attributions. These gaps call for a streaming framework with modest overhead, curvature and drift aware computation, and per-example confidence.
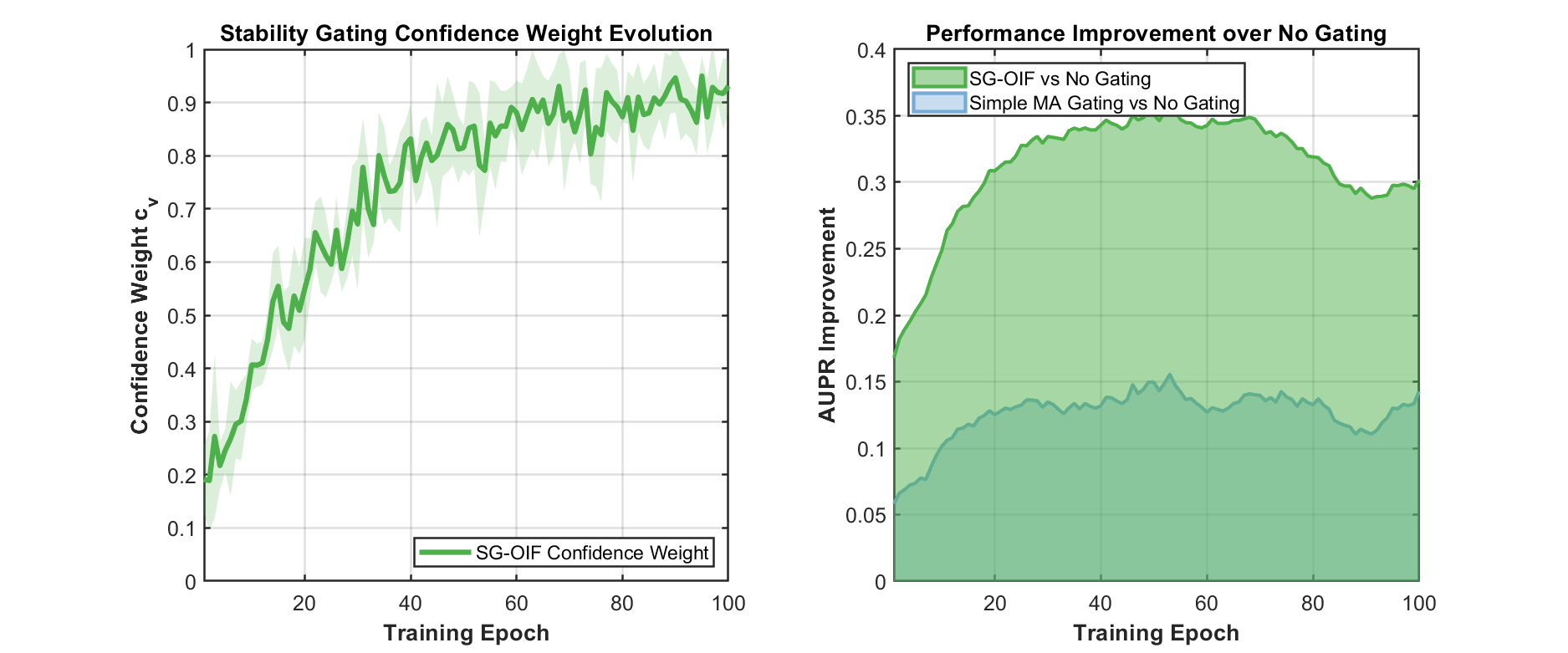
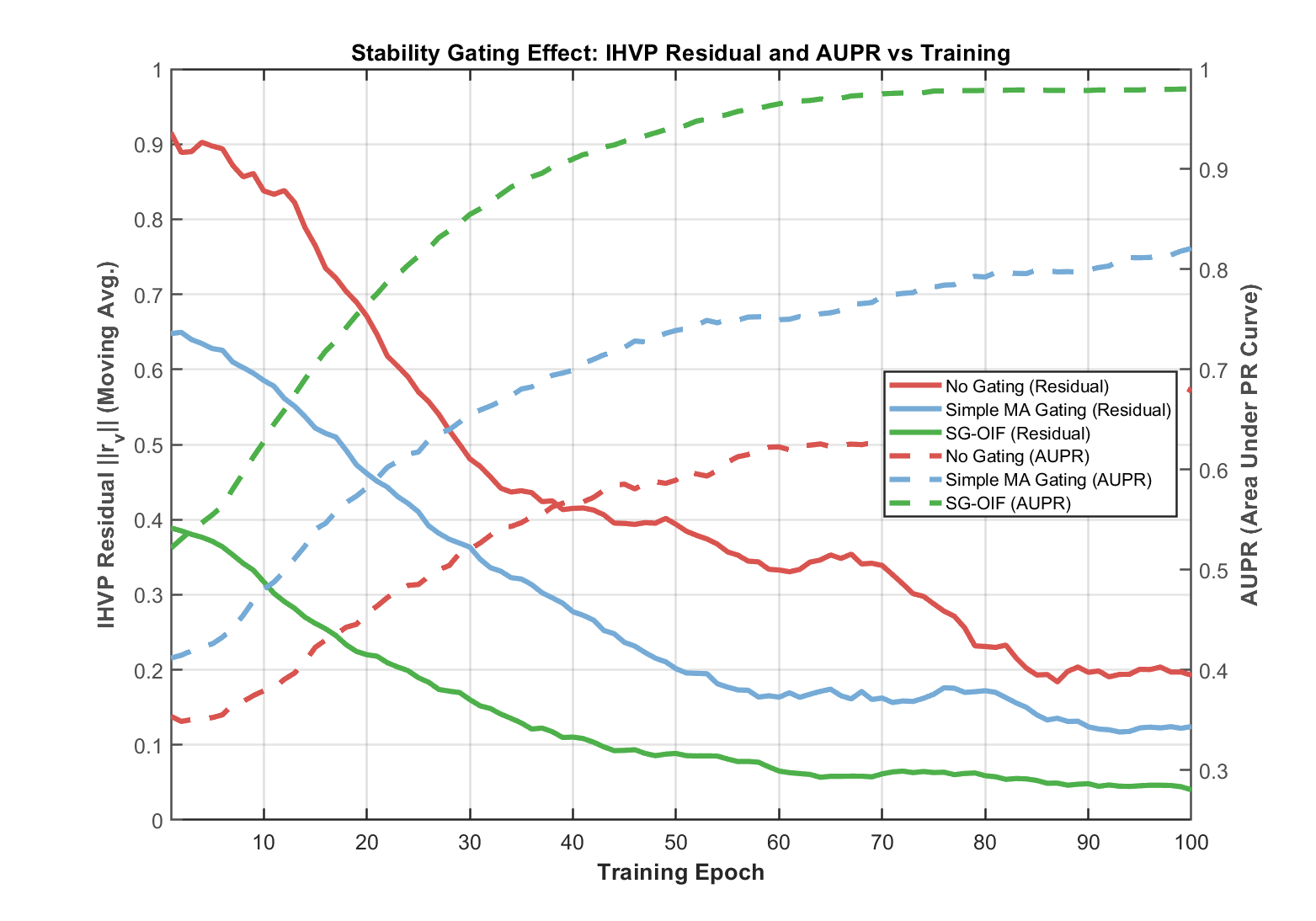
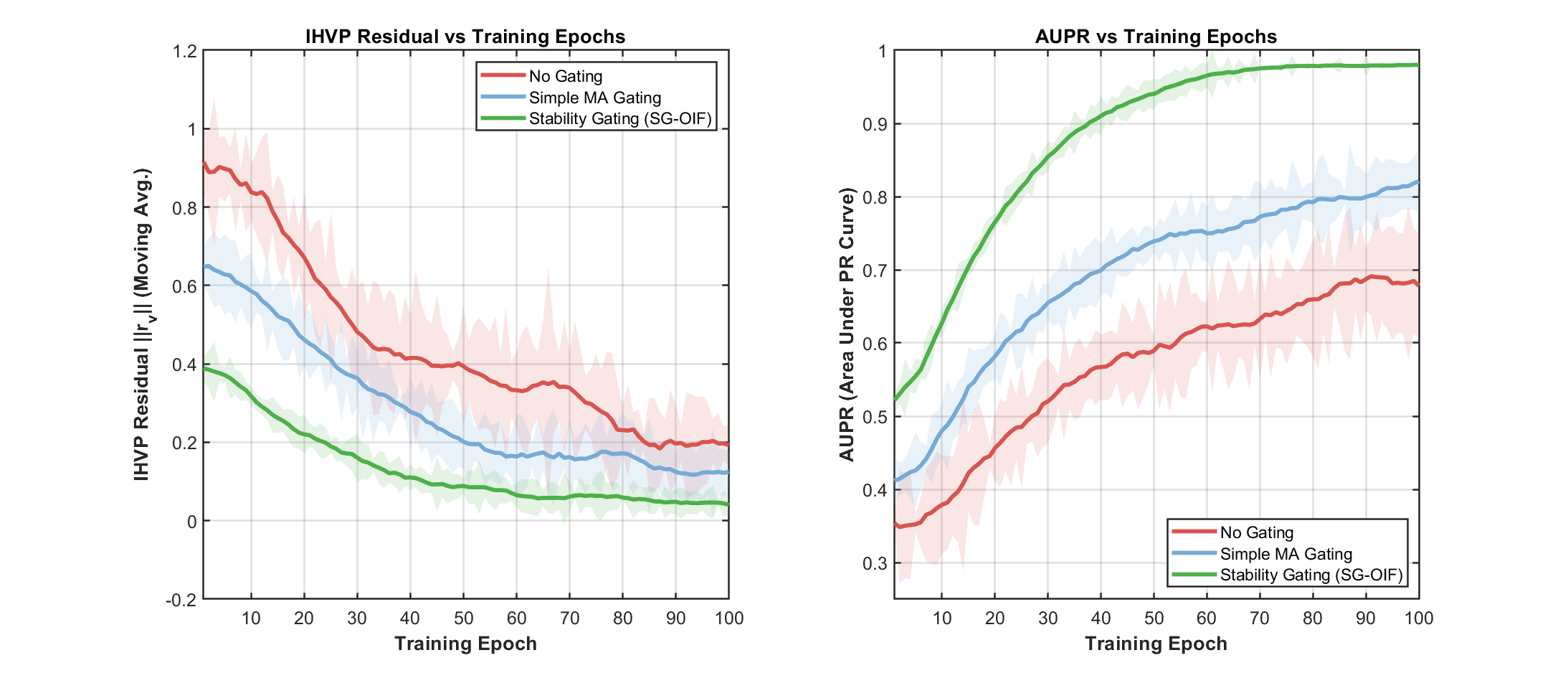
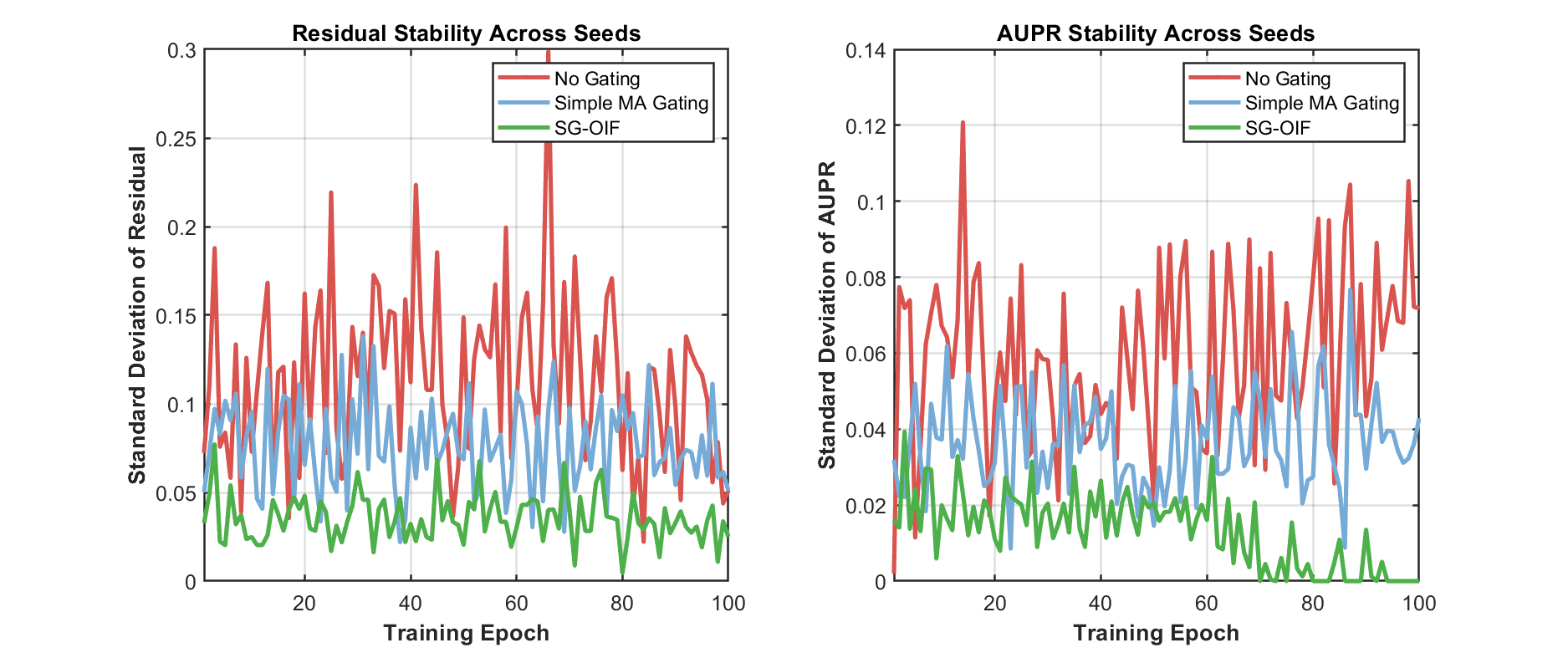
To improve reliable, real-time causal ranking under nonconvex training, we introduce a stability-guided streaming framework that treats algorithmic stability as a confidence modulator for online inverse-curvature computation. At its core, we maintain a lightweight anchor bank and iteratively refine factored inverse Hessian vector directions using stochastic curvature sketching with preconditioned Neumann updates. These updates are steered by stability-inspired signals-gaps between Neumann and Richardson iterates, projected gradient energy, and the variance of stochastic Hessian probes, which adapt truncation depth, step sizes, and the growth of a low-rank subspace, while gating anomalies to suppress numerically unsupported large scores. Building on this, we calibrate per-example confidence via empirical-Ber
This content is AI-processed based on open access ArXiv data.