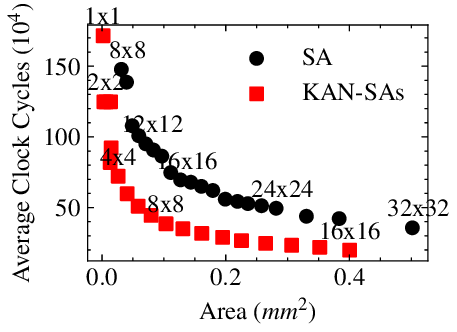
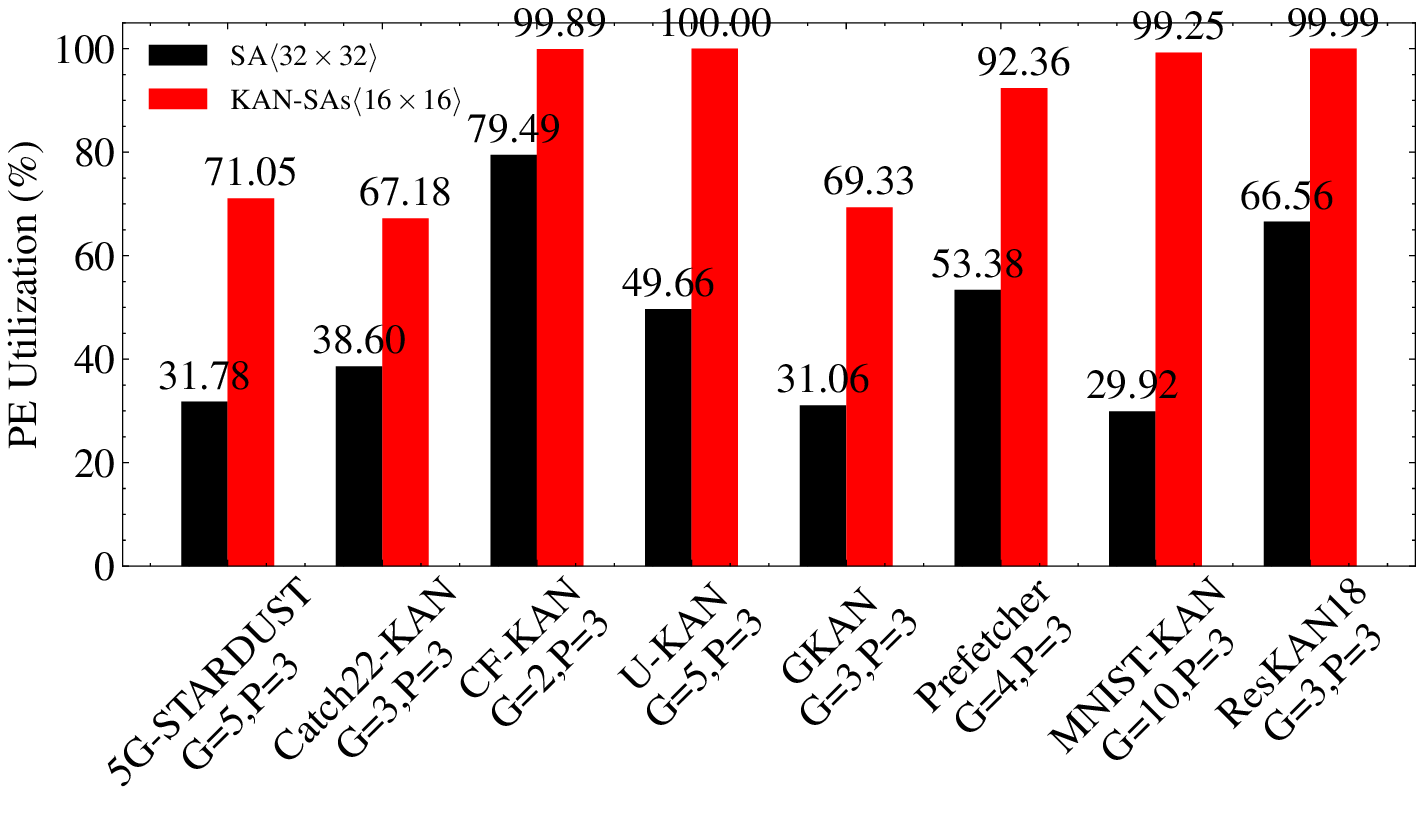
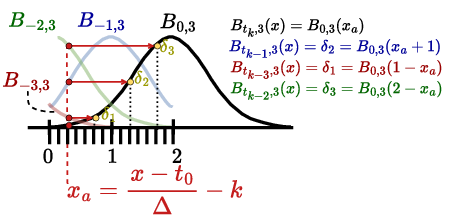Kolmogorov-Arnold Networks (KANs) have garnered significant attention for their promise of improved parameter efficiency and explainability compared to traditional Deep Neural Networks (DNNs). KANs' key innovation lies in the use of learnable non-linear activation functions, which are parametrized as splines. Splines are expressed as a linear combination of basis functions (B-splines). B-splines prove particularly challenging to accelerate due to their recursive definition. Systolic Array (SA)based architectures have shown great promise as DNN accelerators thanks to their energy efficiency and low latency. However, their suitability and efficiency in accelerating KANs have never been assessed. Thus, in this work, we explore the use of SA architecture to accelerate the KAN inference. We show that, while SAs can be used to accelerate part of the KAN inference, their utilization can be reduced to 30%. Hence, we propose KAN-SAs, a novel SA-based accelerator that leverages intrinsic properties of B-splines to enable efficient KAN inference. By including a nonrecursive B-spline implementation and leveraging the intrinsic KAN sparsity, KAN-SAs enhances conventional SAs, enabling efficient KAN inference, in addition to conventional DNNs. KAN-SAs achieves up to 100% SA utilization and up to 50% clock cycles reduction compared to conventional SAs of equivalent area, as shown by hardware synthesis results on a 28nm FD-SOI technology. We also evaluate different configurations of the accelerator on various KAN applications, confirming the improved efficiency of KAN inference provided by KAN-SAs.
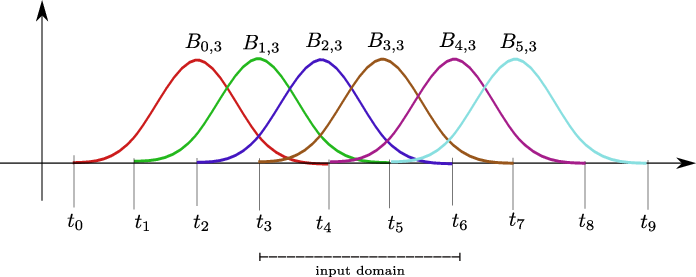
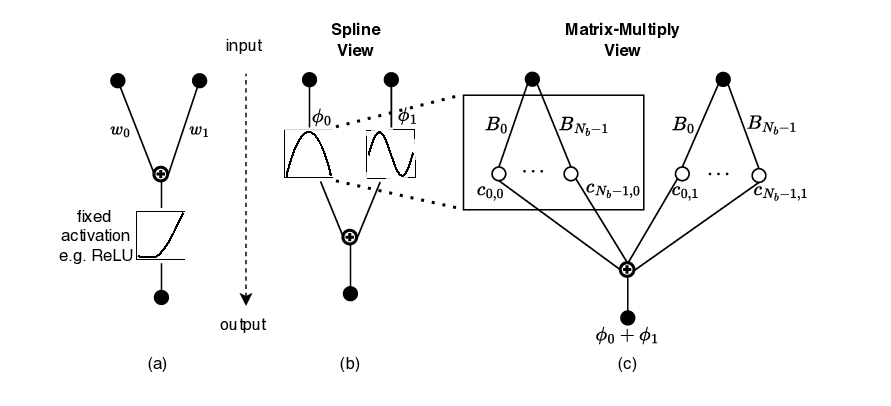
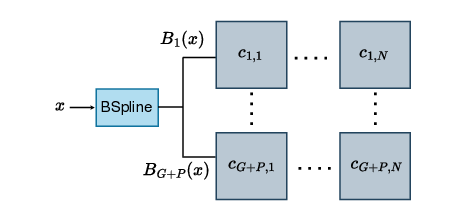
The Kolmogorov-Arnold Network (KAN) is a neural network architecture [1] that has garnered interest and been adopted in various applications, such as time series analysis [2], recommender systems [3], and medical image segmentation [4]. The main interest of KANs lies in their improved parameter efficiency and explainability compared to conventional Deep Neural Networks (DNNs). This is enabled by replacing the conventional scalar weights with learnable spline-based activation functions, which are parameterized in a basis function (B-spline). However, this leads to an increase in computational complexity proportional to the size of the basis. Indeed, to compute KAN inference, instead of a single scalar multiply, each function in the basis must first be evaluated at the input, and then a linear combination of all the basis functions is performed. Moreover, the B-spline functions are evaluated recursively through the Cox-de Boor formula (See Eq. 3), which makes their acceleration challenging.
Recent artificial intelligence (AI) accelerators increasingly rely on spatial architectures, which have become the de facto standard for AI acceleration. Such architectures efficiently execute general 1 The source code will be publicly released upon acceptance. matrix multiplication (GEMM), the core operation underlying many AI workloads. Prominent examples include Google’s Tensor Processing Unit (TPU) [5] and NVIDIA’s Tensor Cores, first introduced in the Volta GPU microarchitecture [6]. The efficiency of spatial architectures stems from their ability to maximize data reuse and minimize data movement, which dominates the energy cost [7]. Building on this foundation, numerous works have proposed further optimizations tailored to specific workloads. For instance, Eyeriss [8] introduced dataflow optimizations to improve the efficiency of convolutional neural networks. Other efforts, such as SCNN [9], explored computation on compressed weights and activations to exploit zero weights stemming from model pruning and zero activations that occur in ReLU-based networks. The unique design of KANs limits the effectiveness of existing solutions in accelerating KAN inference compared to other AI applications. Specifically, the recursive nature of B-spline function computation creates a considerable bottleneck, making it challenging to take full advantage of the efficient GEMM executions in spatial architectures such as modern GPUs or Systolic Arrays (SAs) [10], which are the foundation of modern TPUs.
Therefore, research efforts have been focusing on new approaches to accelerate KANs (details in Sec. II-B). Among recent studies, compute-in-memory (CIM) approaches have been proposed [11], [12]. In such studies, different ways to approximate the learned non-linear KAN functions or their basis are utilized, such as piece-wise linear (PWL) approximation. However, no insights are offered into how spatial (non-CIM) architectures may be optimized for KANs. A recent approach, ArKANe [13], focuses on the B-spline evaluation bottleneck. It proposes an efficient dataflow acceleration methods for the Cox-de Boor recursive formula, achieving a considerable speedup compared to CPU and GPU implementations. While all these efforts considerably improve knowledge of KAN acceleration, unfortunately, the current literature lacks solutions to efficiently accelerate KANs on spatial architectures, and particularly on SAs. To address this gap, this paper analyzes and utilizes the KAN properties to enhance SAs, enabling efficient end-to-end inference acceleration of KAN while maintaining the generality of the accelerator for non-KAN DNN workloads.
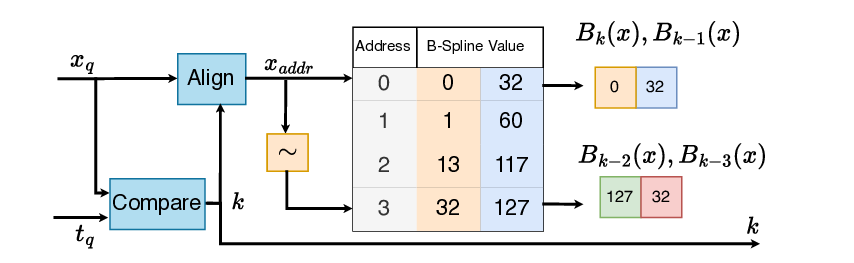
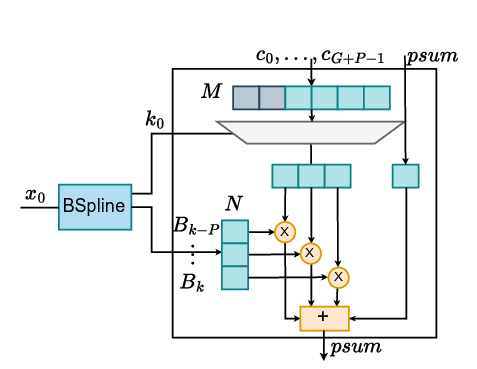
As shown in Section III, once the B-splines have been evaluated, their linear combination is nothing more than a GEMM operation, which can be accelerated on SAs. Regarding the B-spline computation, we observe that a direct floating-point implementation of the recursive evaluation of B-splines is quite costly. For inferenceonly acceleration, an efficient tabulation strategy of B-splines is possible, thanks to their properties [12]. Furthermore, B-spline computation results in an N :M sparsity pattern in the values processed by the SA, thereby leading to low Processing Element (PE) utilization. Designing a PE of the SA that can handle inputs with a KAN-specific N :M sparsity pattern is needed to improve the overall efficiency of the SA [14]. To the best of our knowledge, there is currently no SA-based accelerator that, in addition to standard DNN workloads, can accelerate KANs by utilizing nonrecursive B-spline computation and achieving high PE utilization. In summary, this work makes the following contributions:
• We show how a KAN layer can be transformed into a GEMM formulation for execution on a systolic array, and analyze the causes of the inefficiencies that lead to low throughput and poor PE utilization.
• Building upon our analysis, we include in KAN-SAs the needed architectural modifications to handle su
This content is AI-processed based on open access ArXiv data.