Tractable Weighted First-Order Model Counting with Bounded Treewidth Binary Evidence

📝 Original Info

• Title: Tractable Weighted First-Order Model Counting with Bounded Treewidth Binary Evidence
• ArXiv ID: 2511.09174
• Date: 2025-11-12
• Authors: ** 제공된 논문 정보에 저자명은 명시되어 있지 않습니다. (필요 시 원문을 확인해 주세요.) **

📝 Abstract

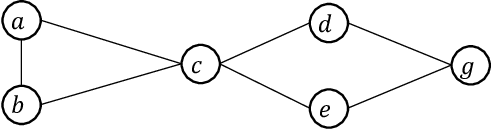
The Weighted First-Order Model Counting Problem (WFOMC) asks to compute the weighted sum of models of a given first-order logic sentence over a given domain. Conditioning WFOMC on evidence -- fixing the truth values of a set of ground literals -- has been shown impossible in time polynomial in the domain size (unless $\mathsf{\#P \subseteq FP}$) even for fragments of logic that are otherwise tractable for WFOMC without evidence. In this work, we address the barrier by restricting the binary evidence to the case where the underlying Gaifman graph has bounded treewidth. We present a polynomial-time algorithm in the domain size for computing WFOMC for the two-variable fragments $\text{FO}^2$ and $\text{C}^2$ conditioned on such binary evidence. Furthermore, we show the applicability of our algorithm in combinatorial problems by solving the stable seating arrangement problem on bounded-treewidth graphs of bounded degree, which was an open problem. We also conducted experiments to show the scalability of our algorithm compared to the existing model counting solvers.

💡 Deep Analysis

📄 Full Content

📸 Image Gallery

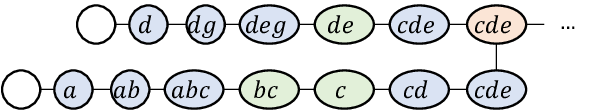
Reference