Bi-Objective Evolutionary Optimization for Large-Scale Open Pit Mine Scheduling Problem under Uncertainty with Chance Constraints

February 22, 2026

Reading time: 2 minute

...

📝 Original Info

Title: Bi-Objective Evolutionary Optimization for Large-Scale Open Pit Mine Scheduling Problem under Uncertainty with Chance Constraints
ArXiv ID: 2511.08275
Date: 2025-11-11
Authors: 정보 없음 (논문에 명시된 저자 정보가 제공되지 않았습니다)

📝 Abstract

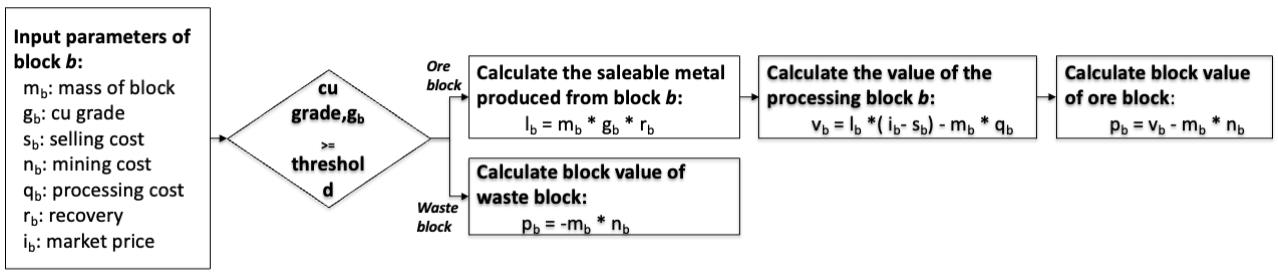
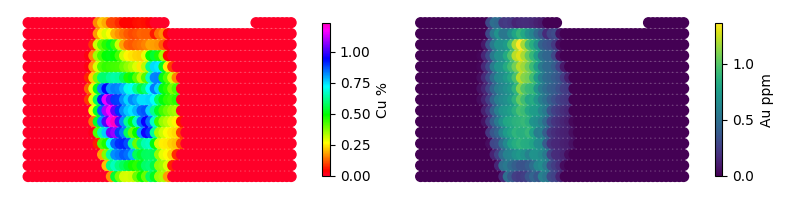
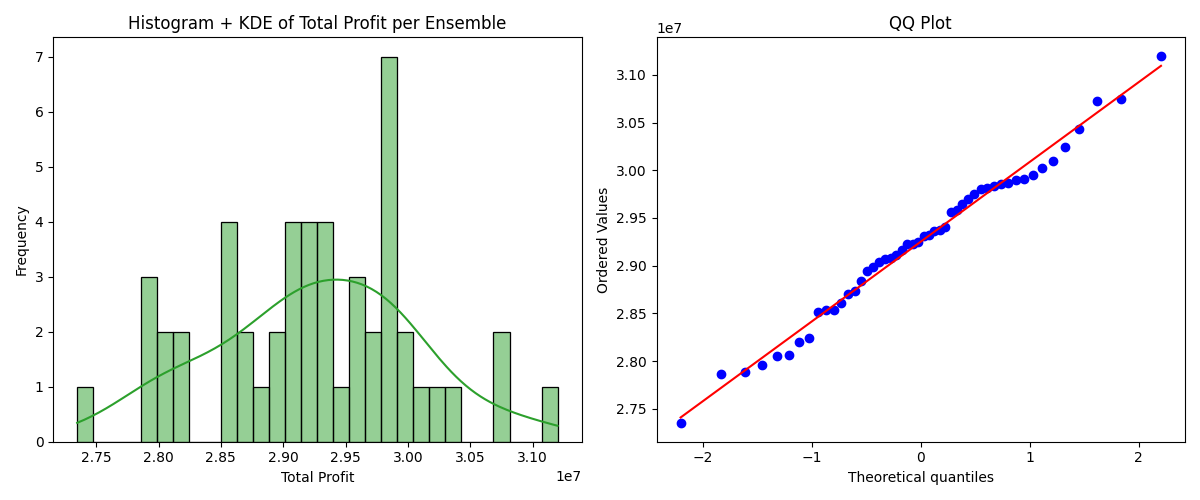
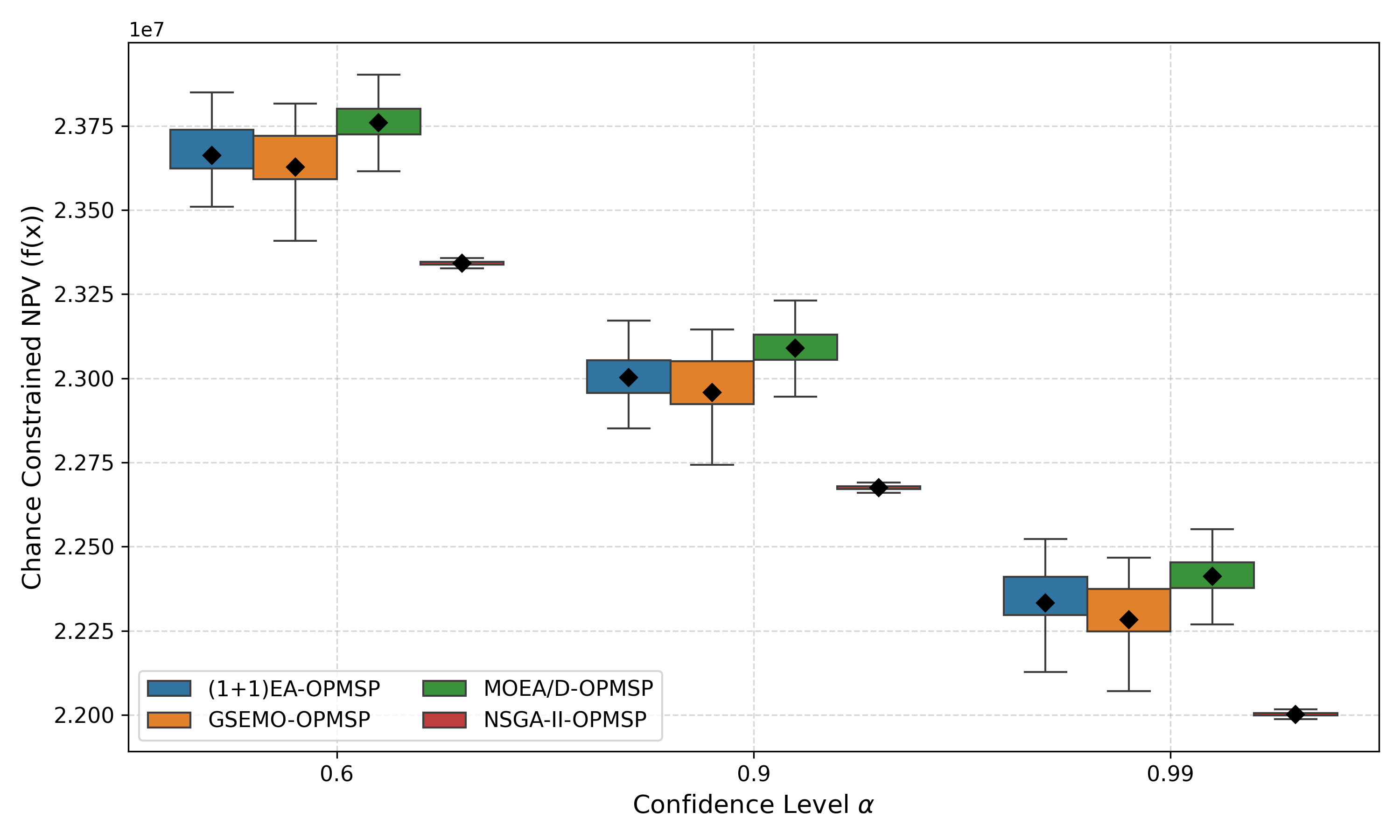
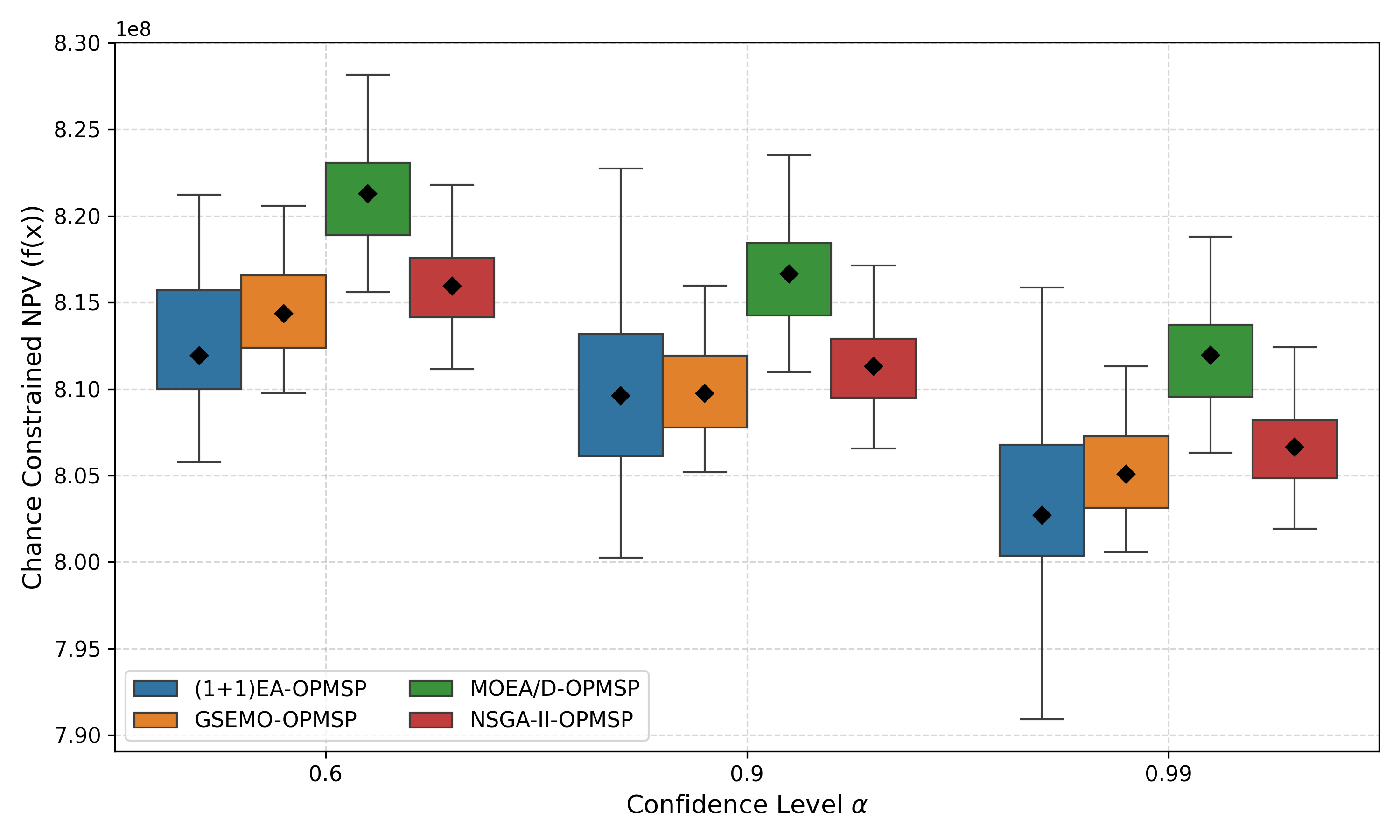
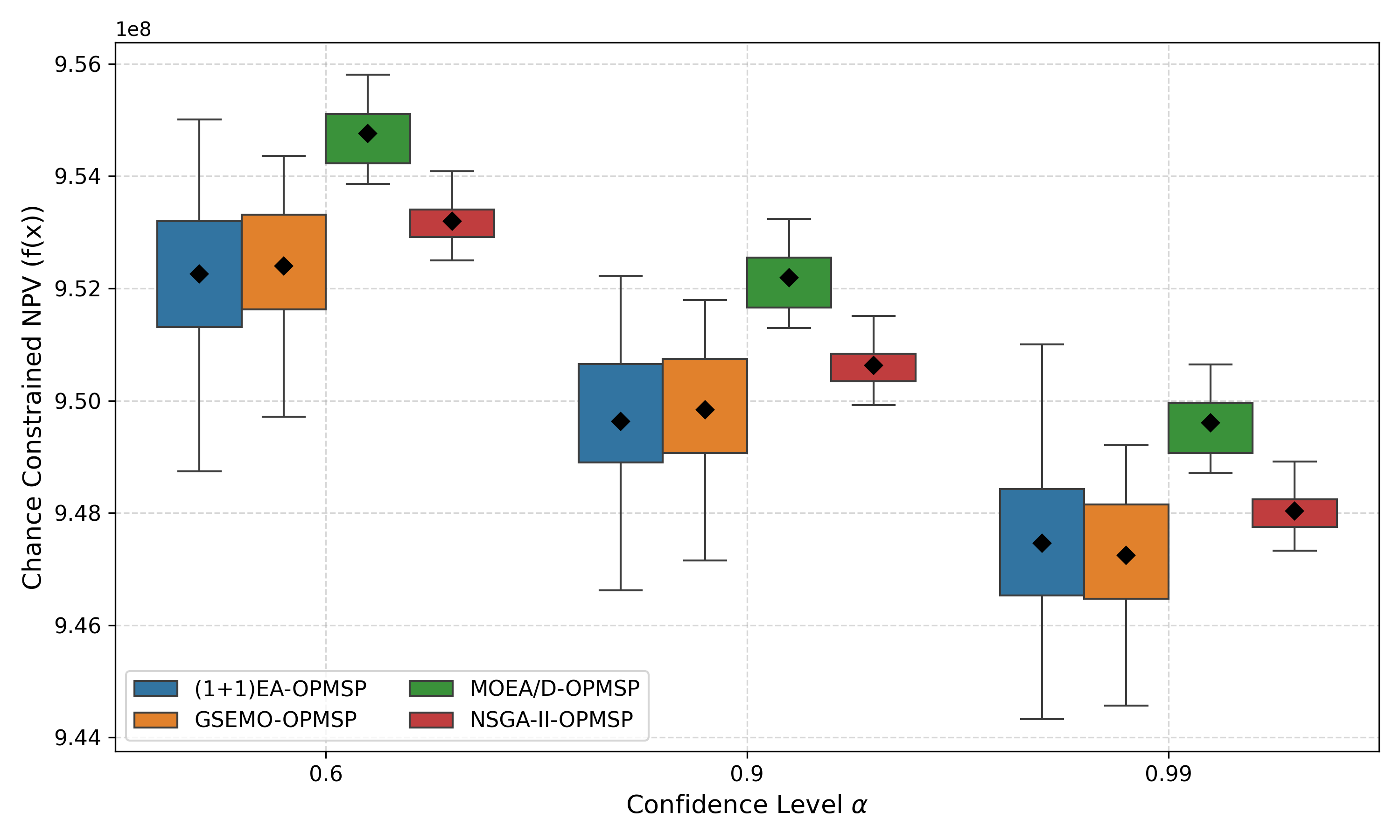
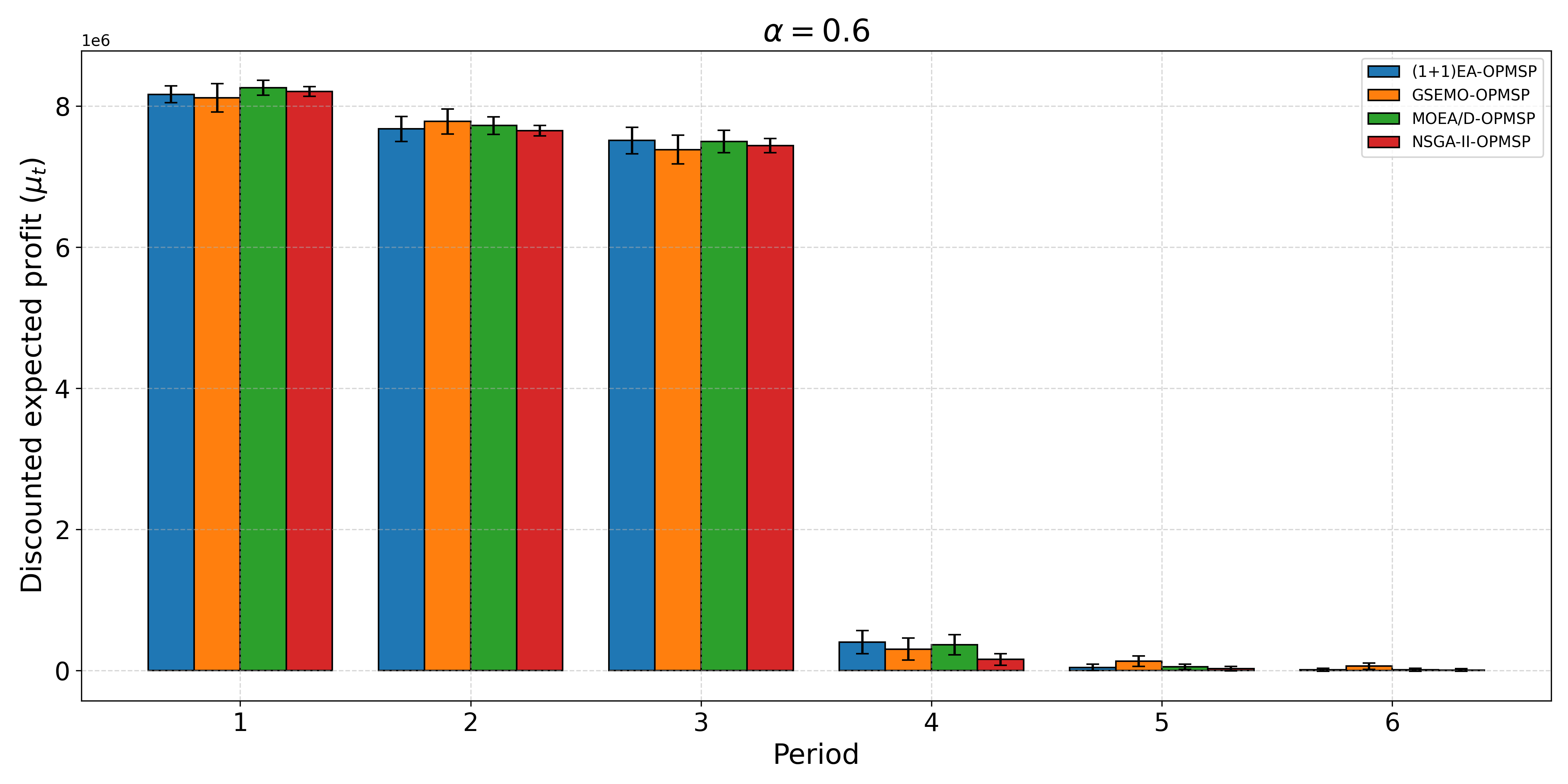
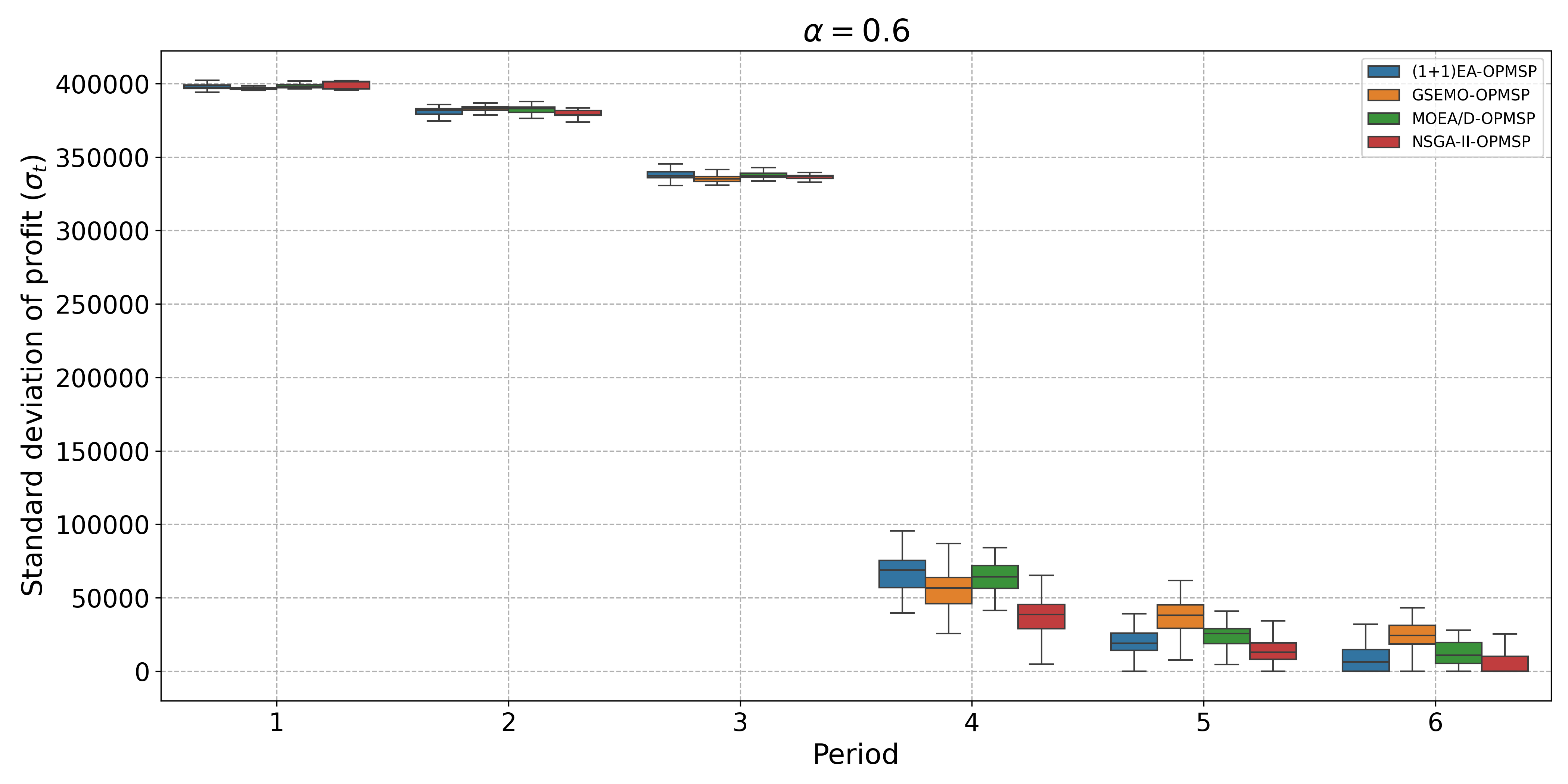
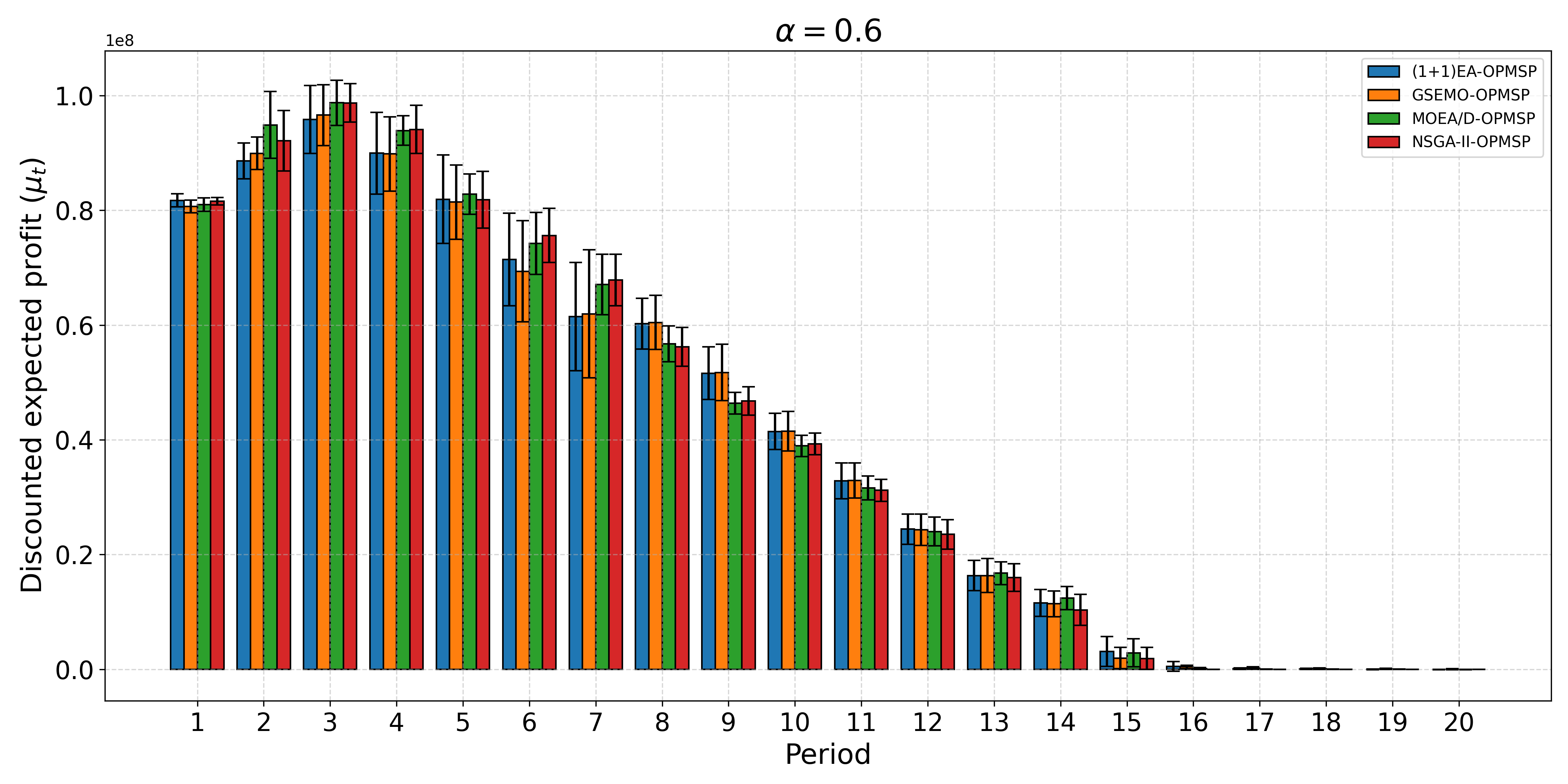
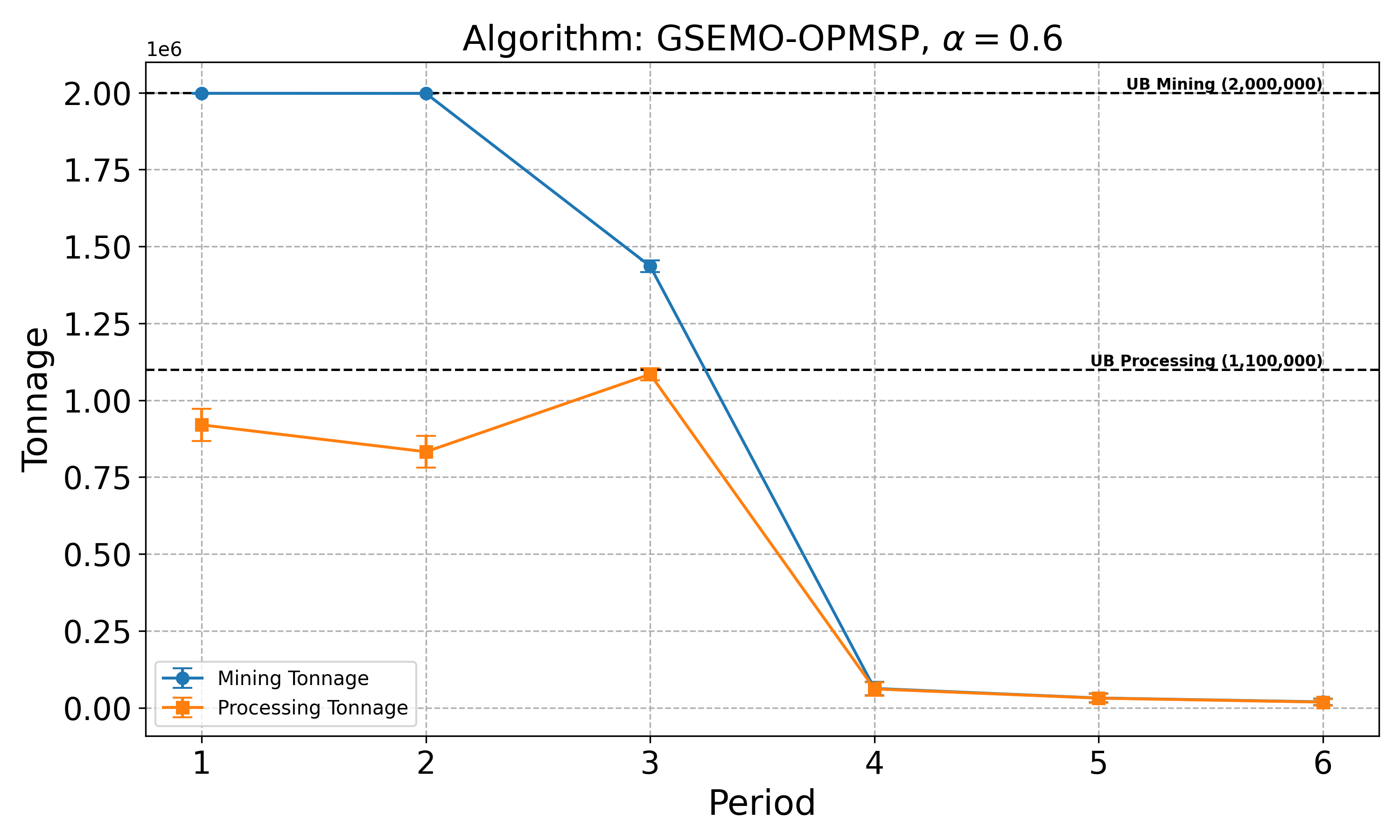
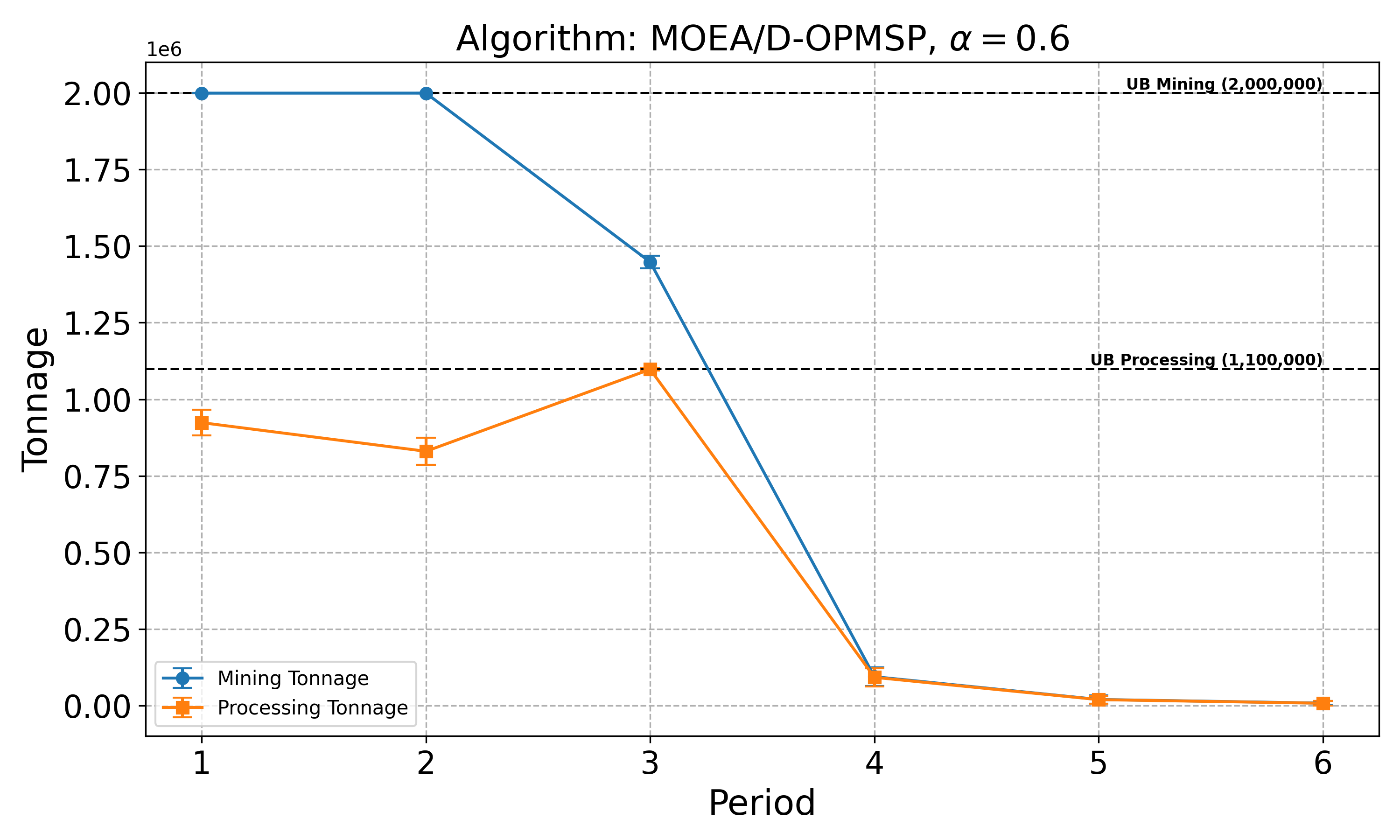
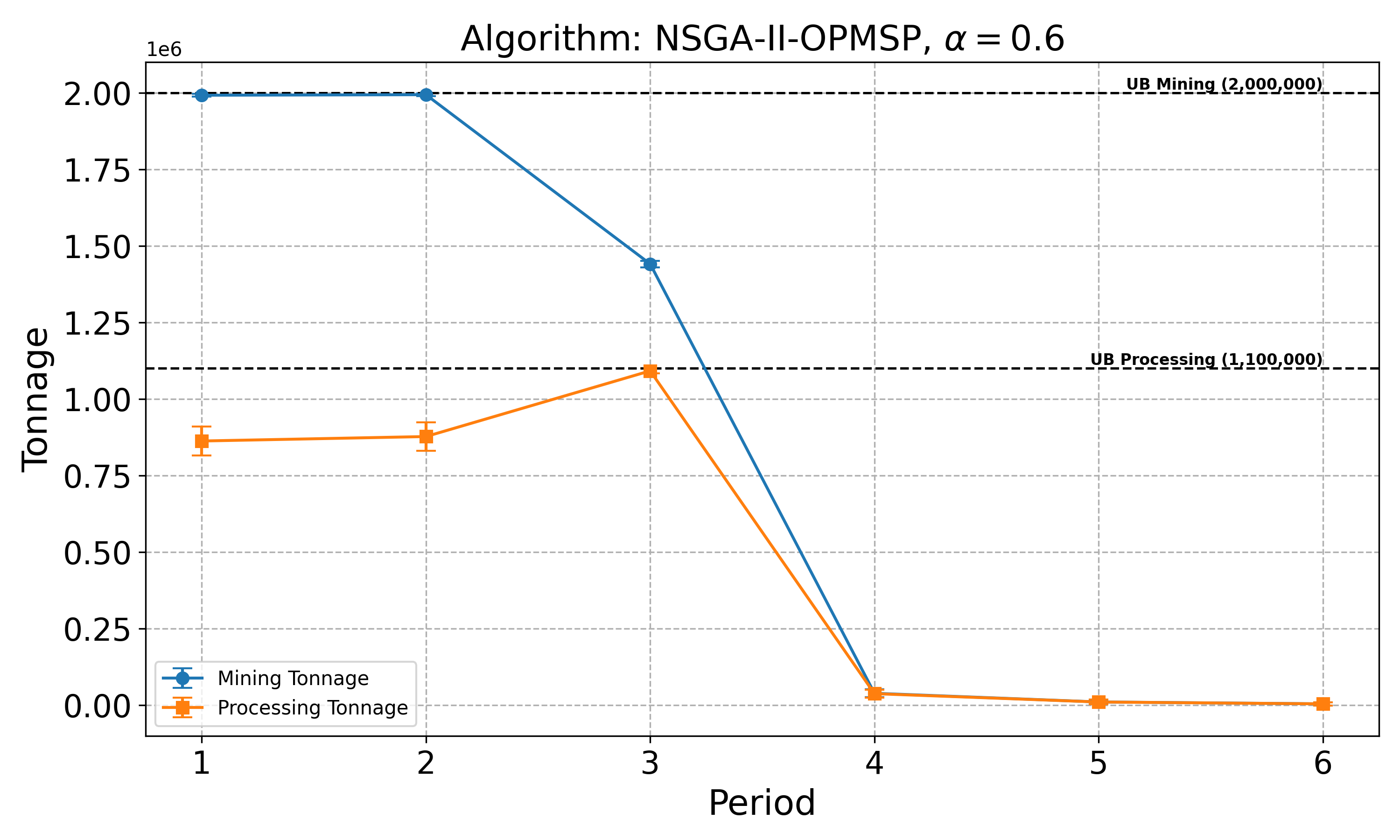
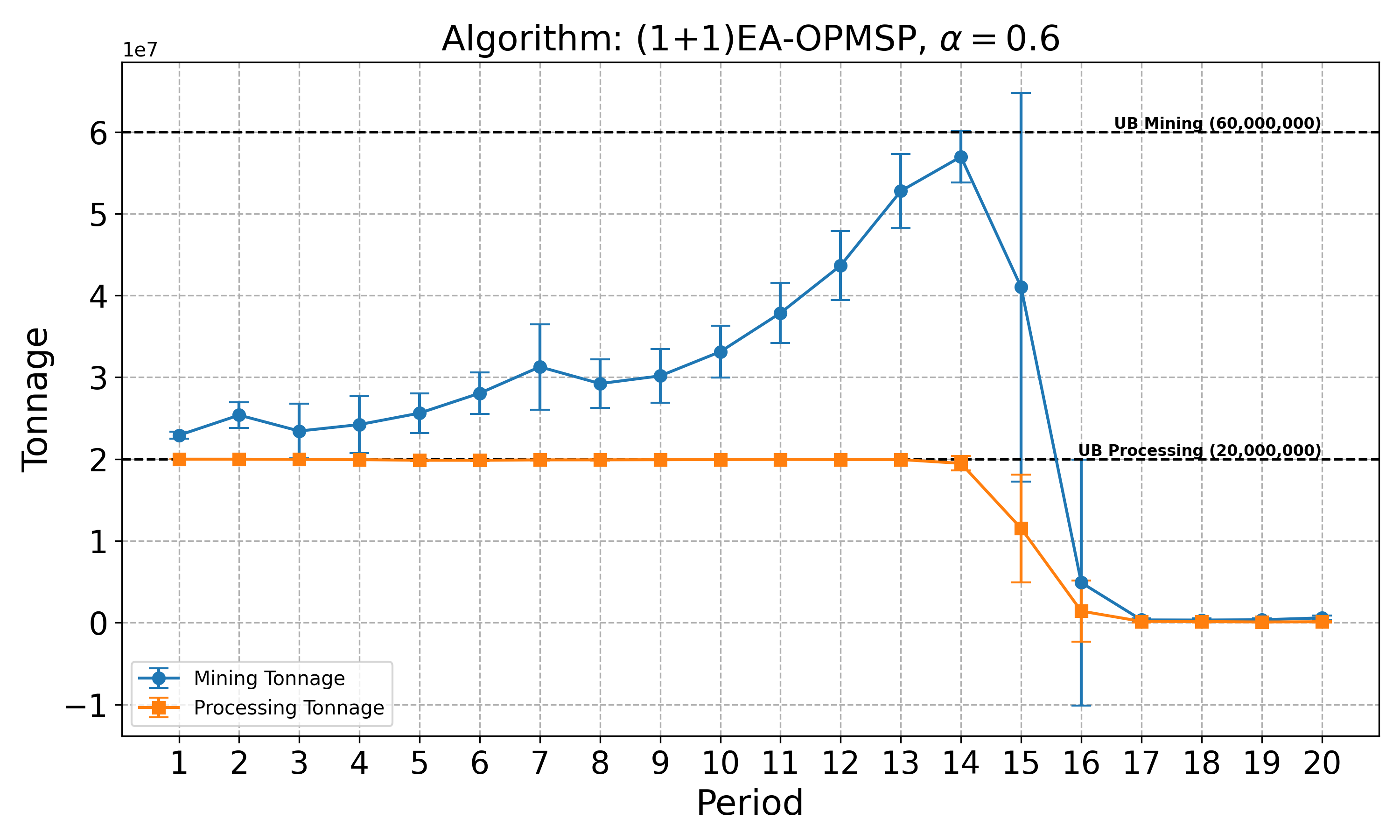
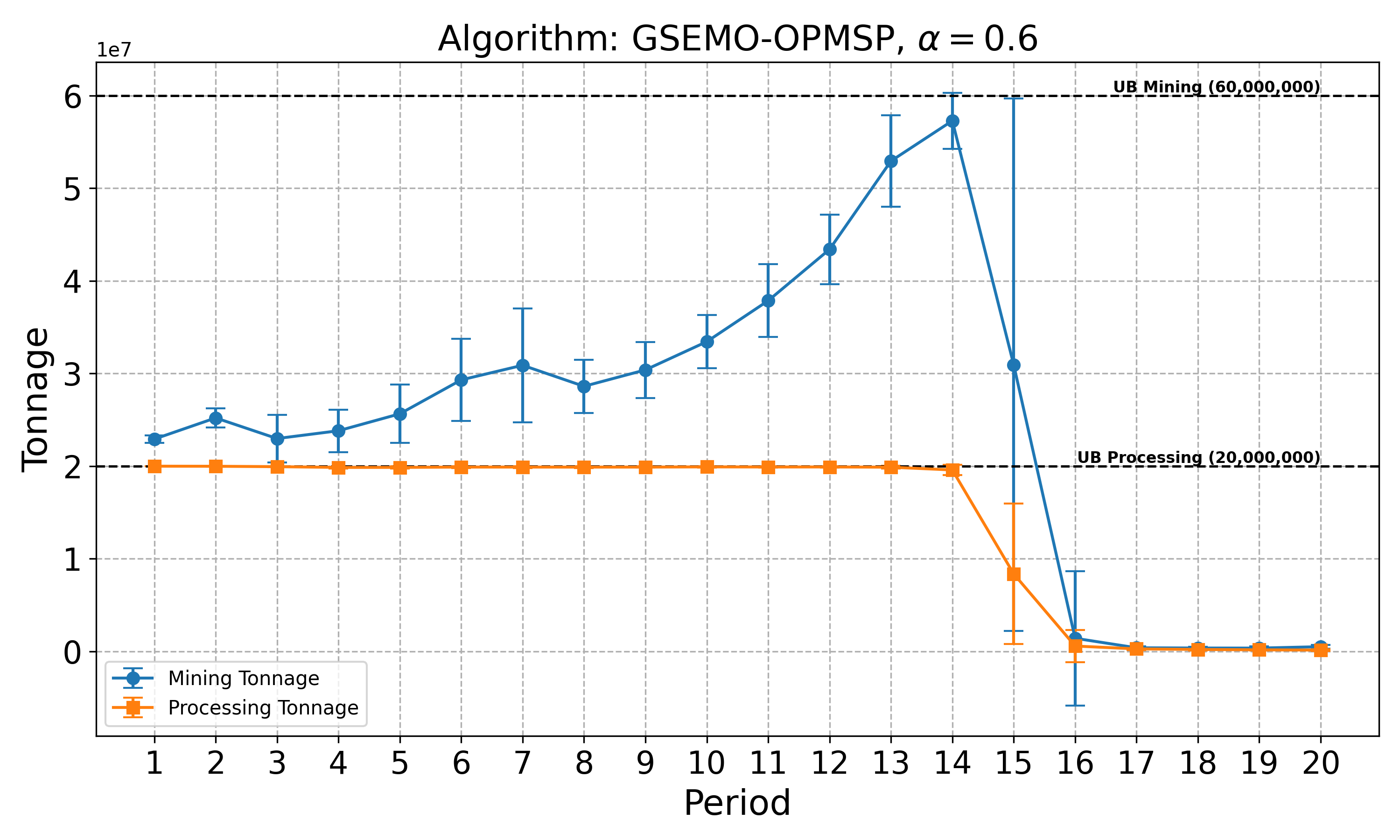
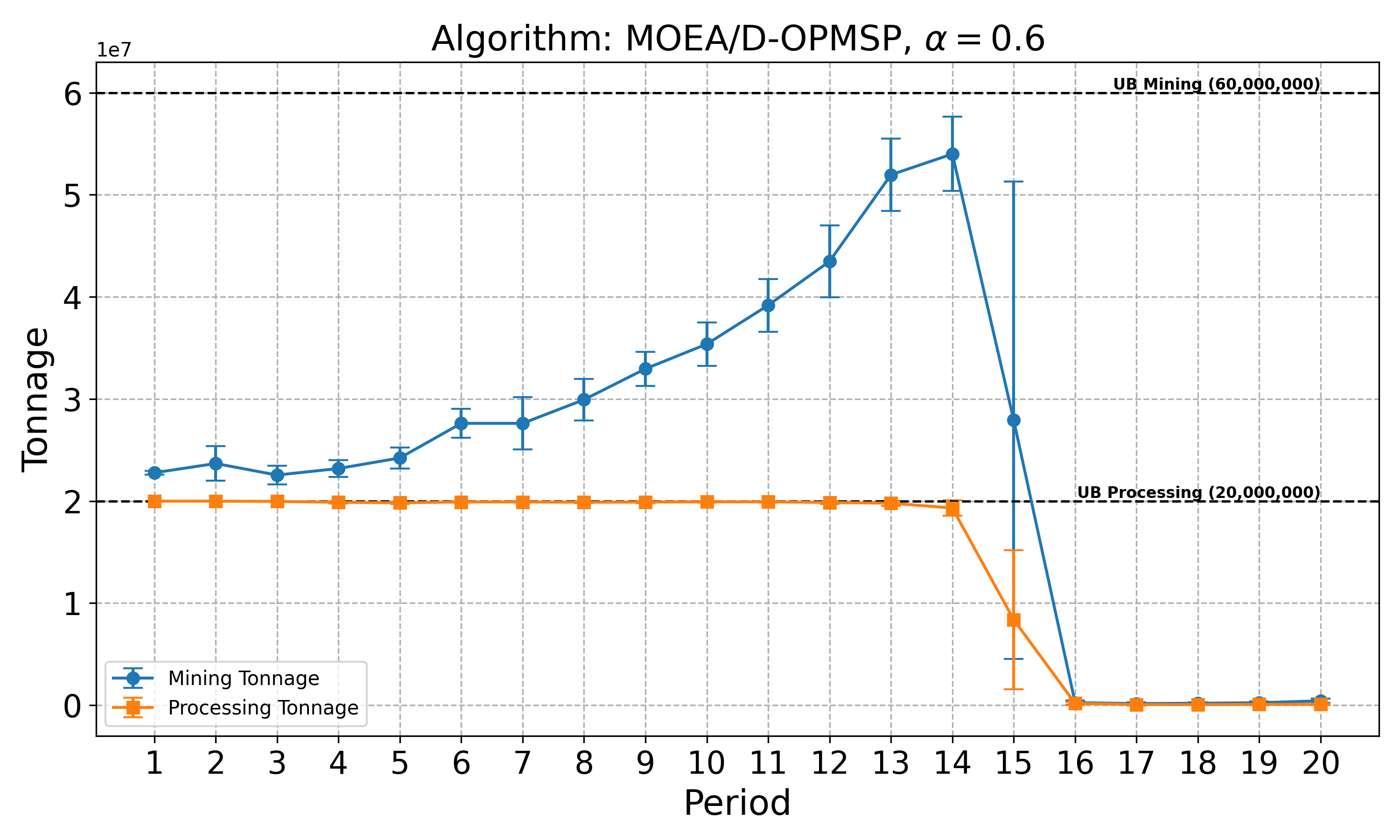
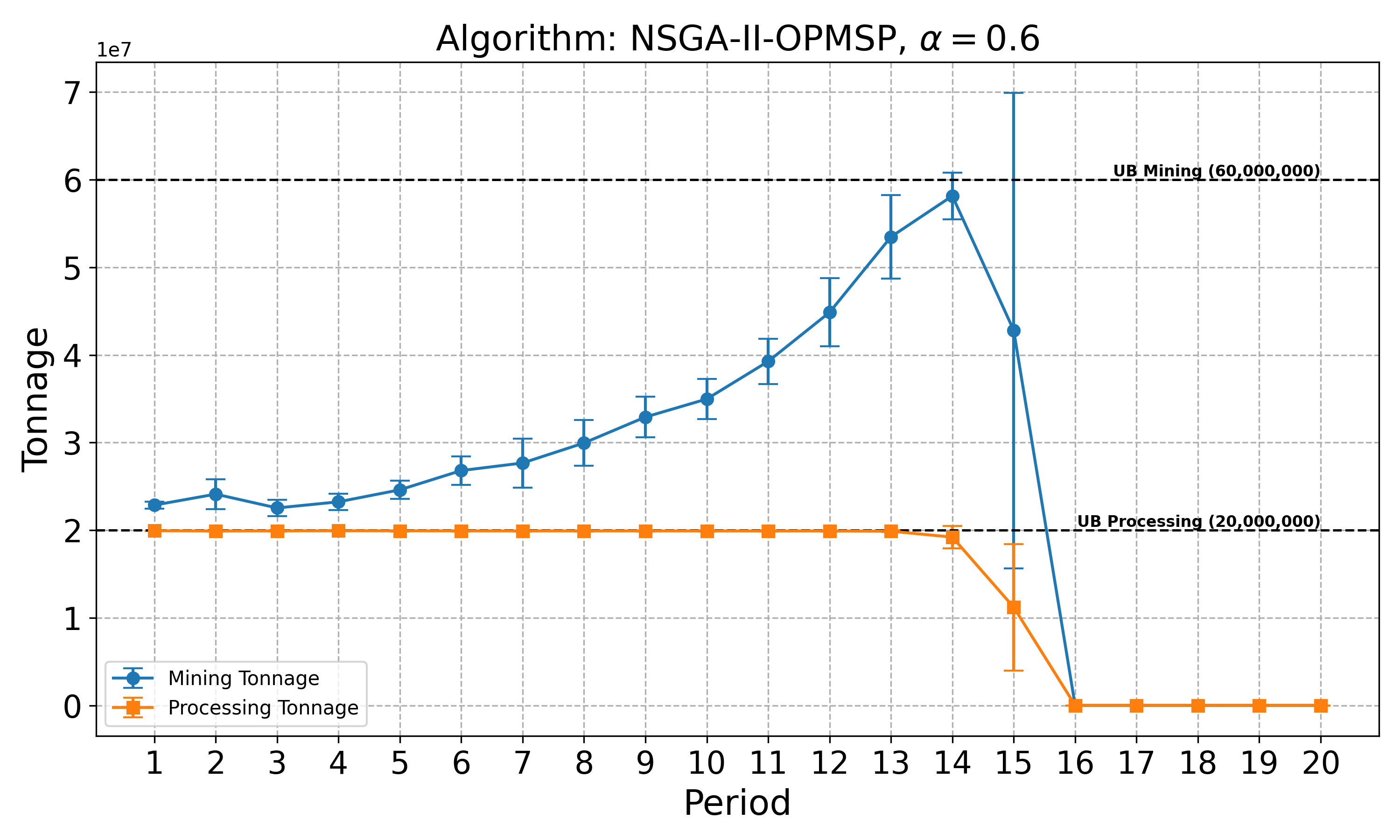
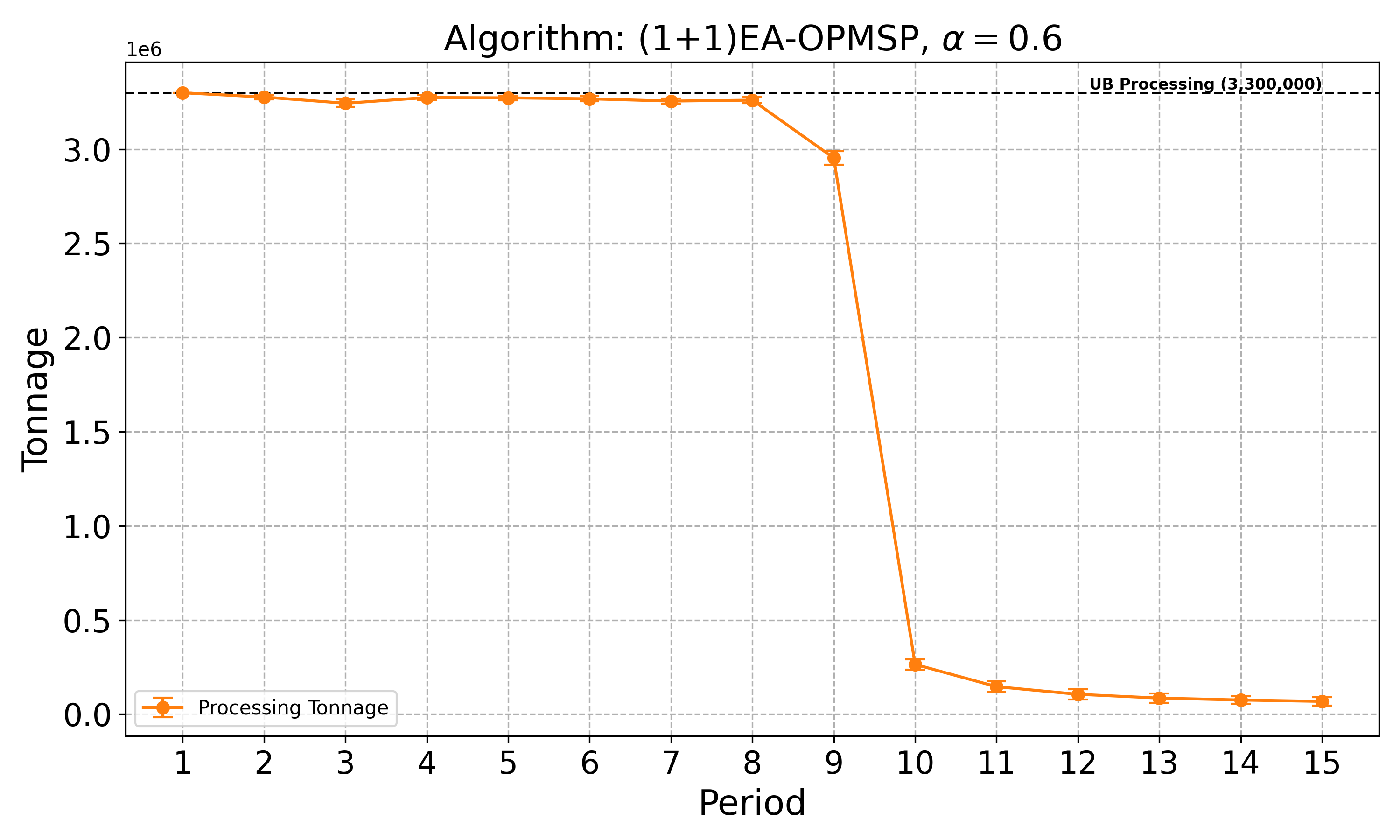
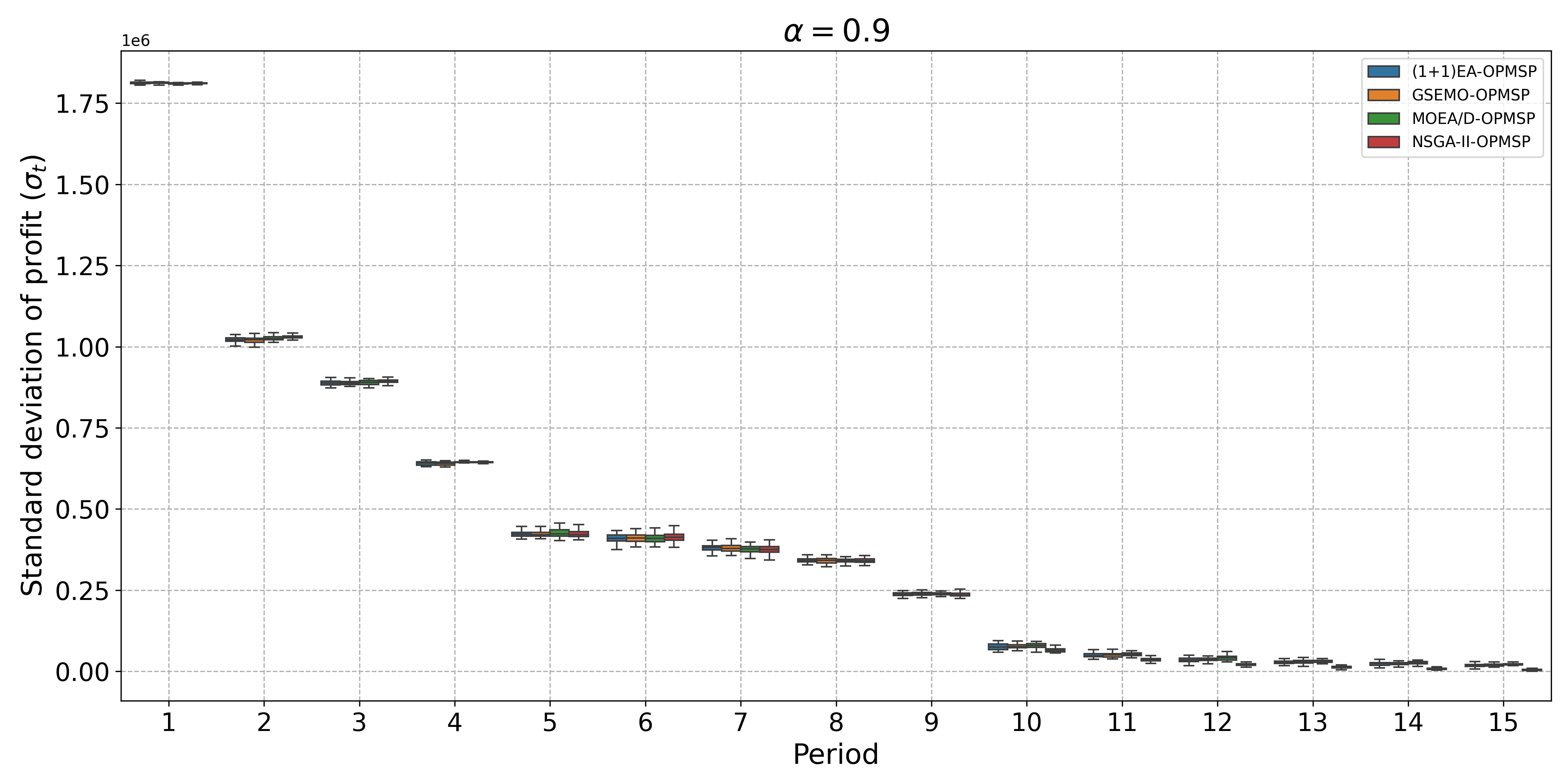
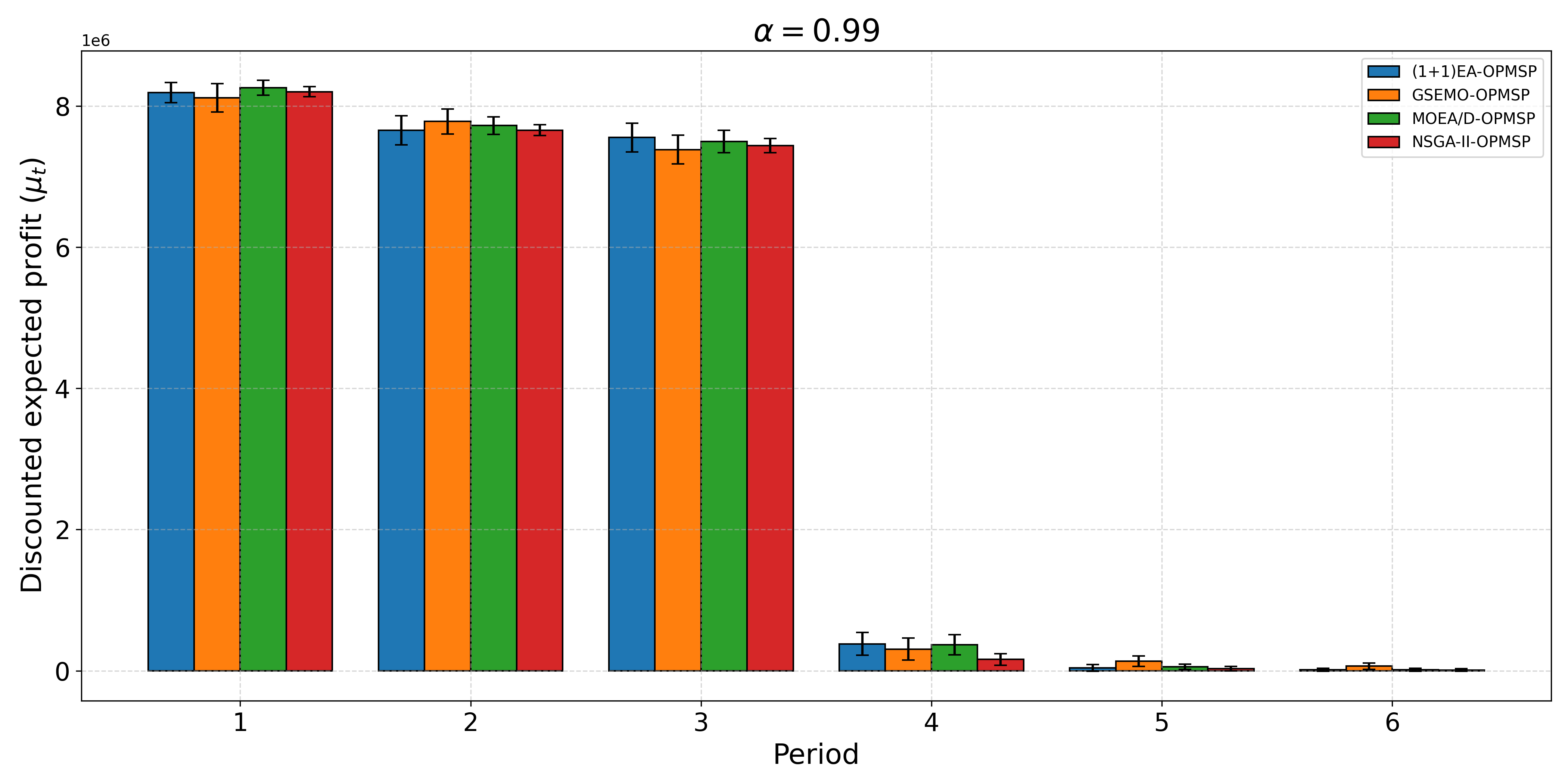
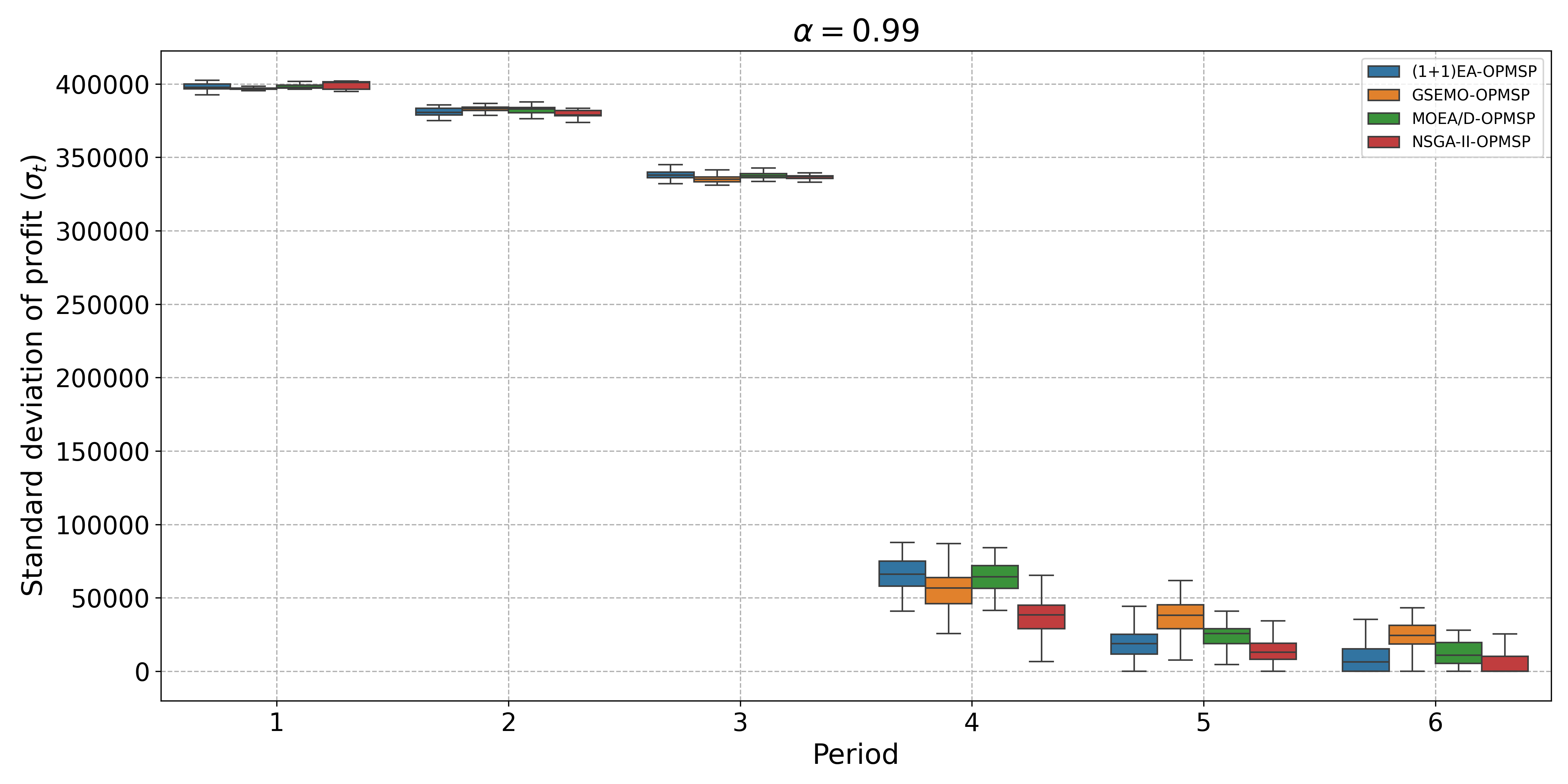
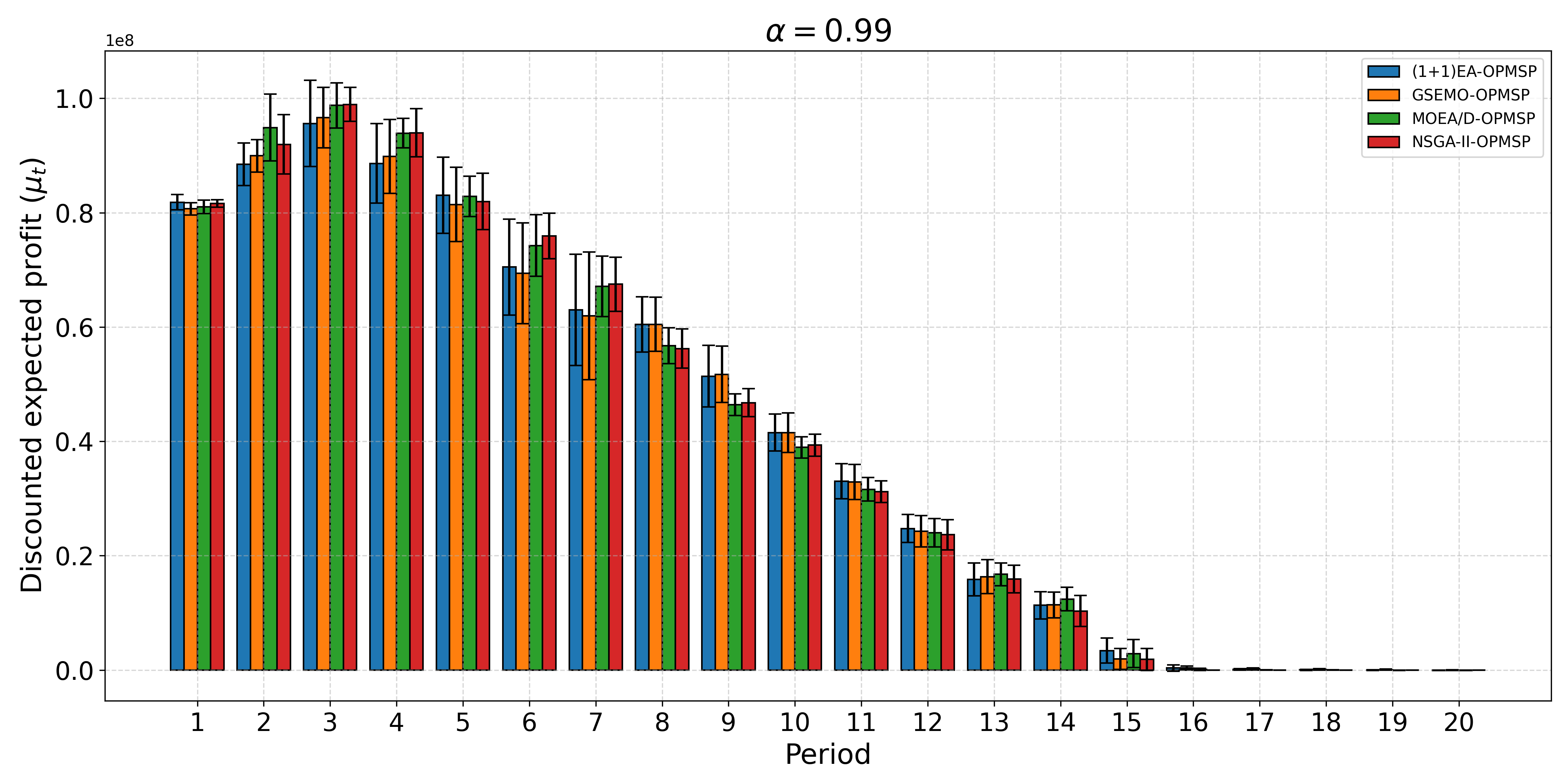
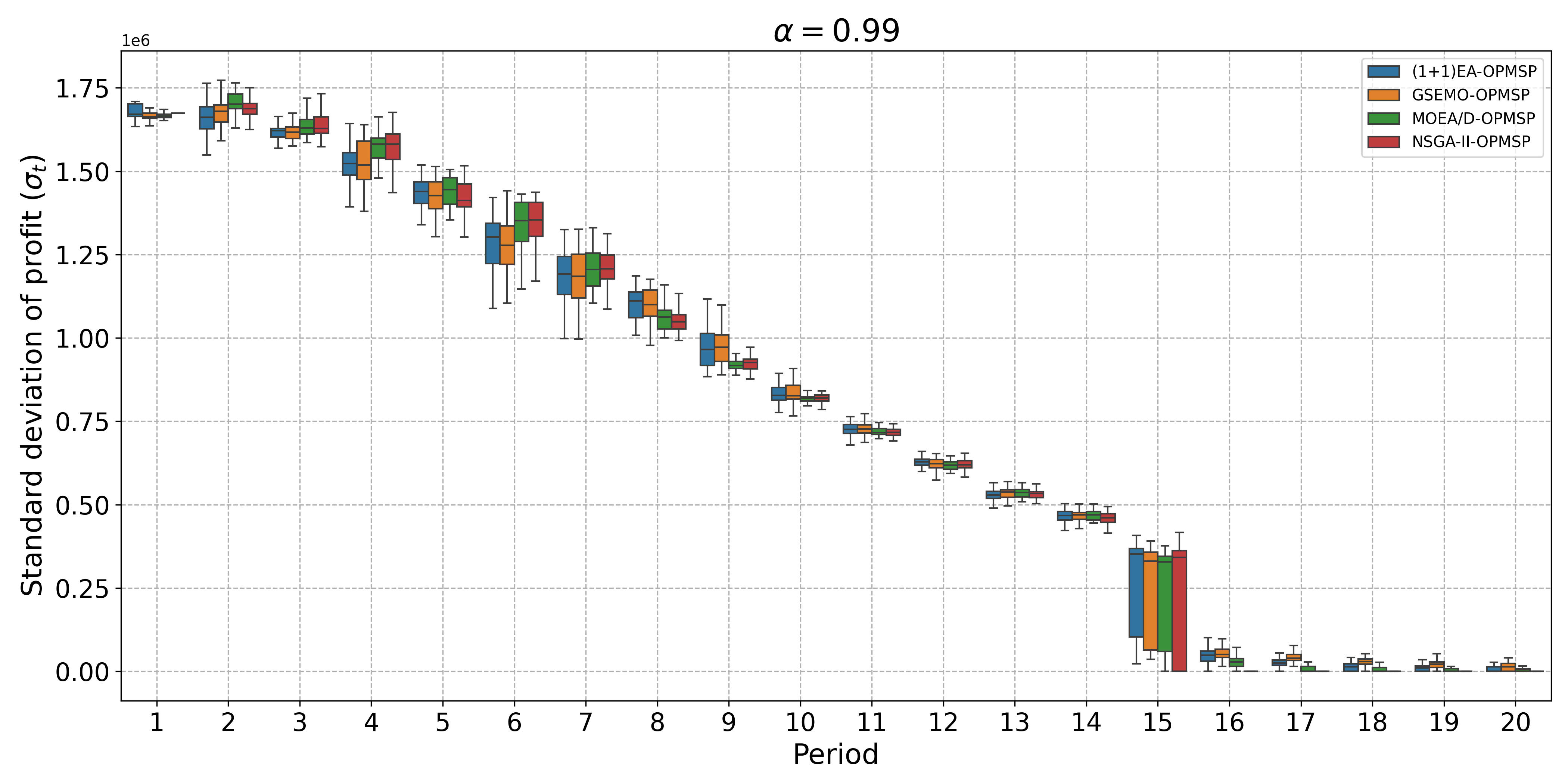
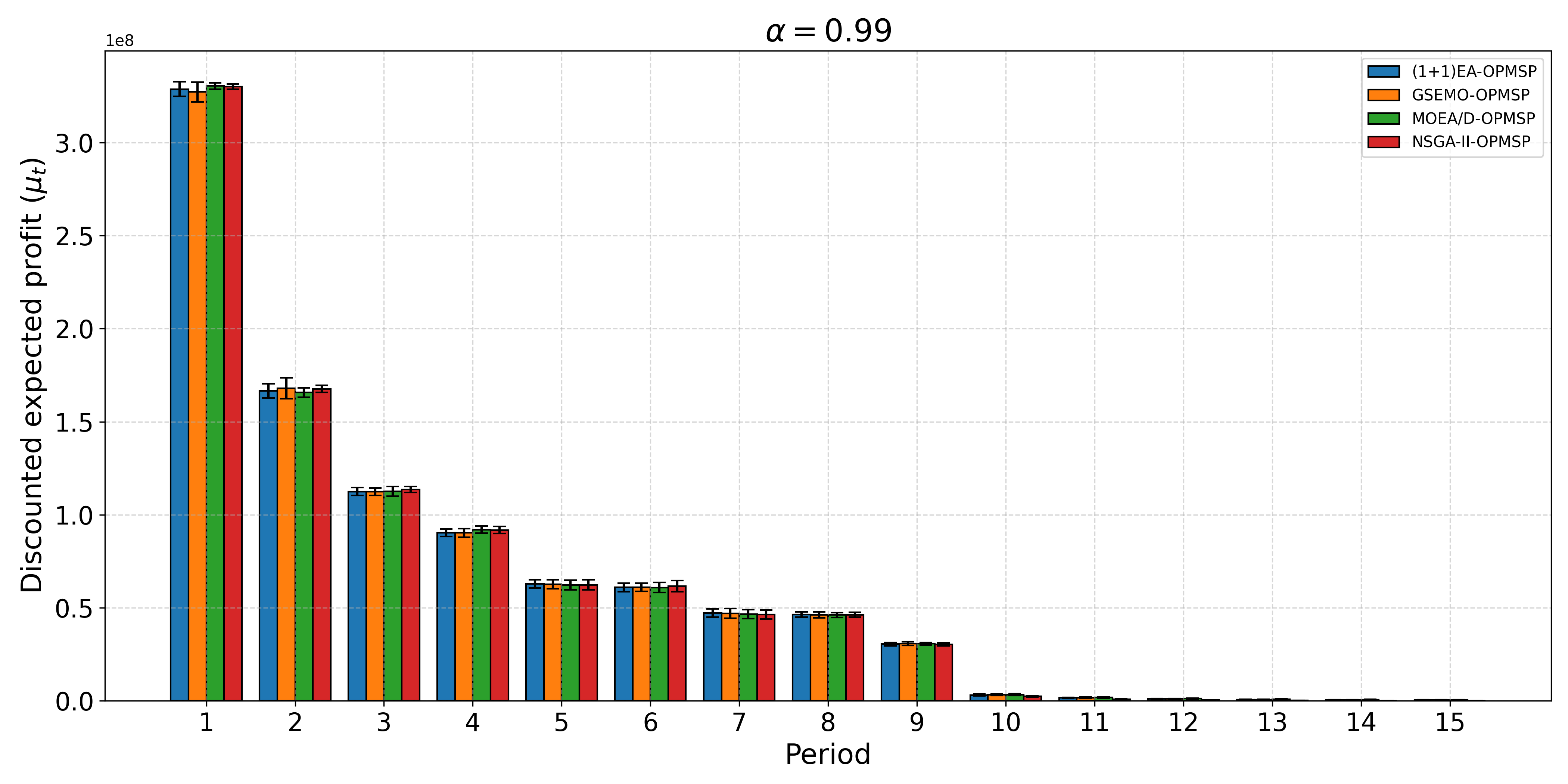
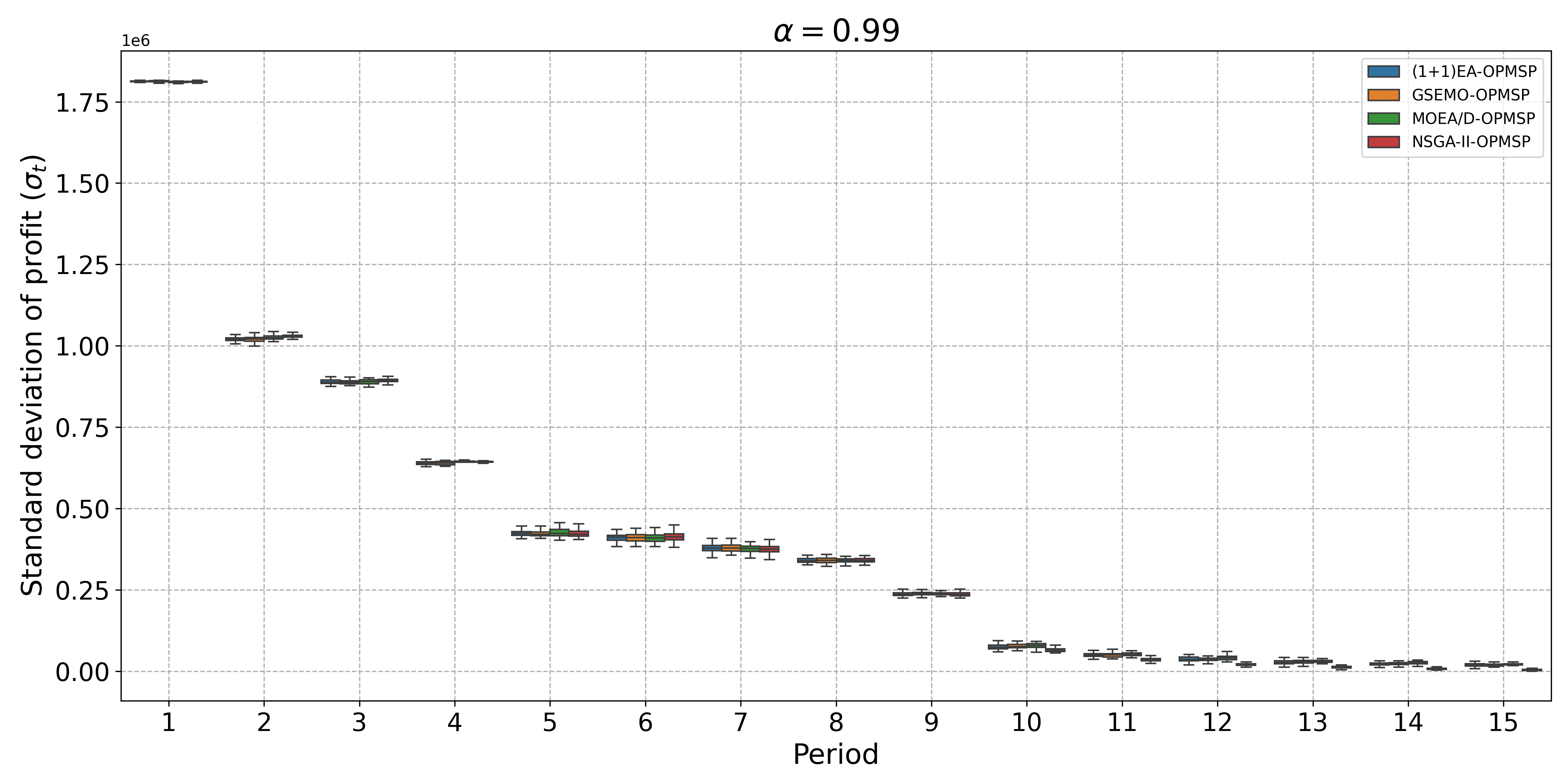
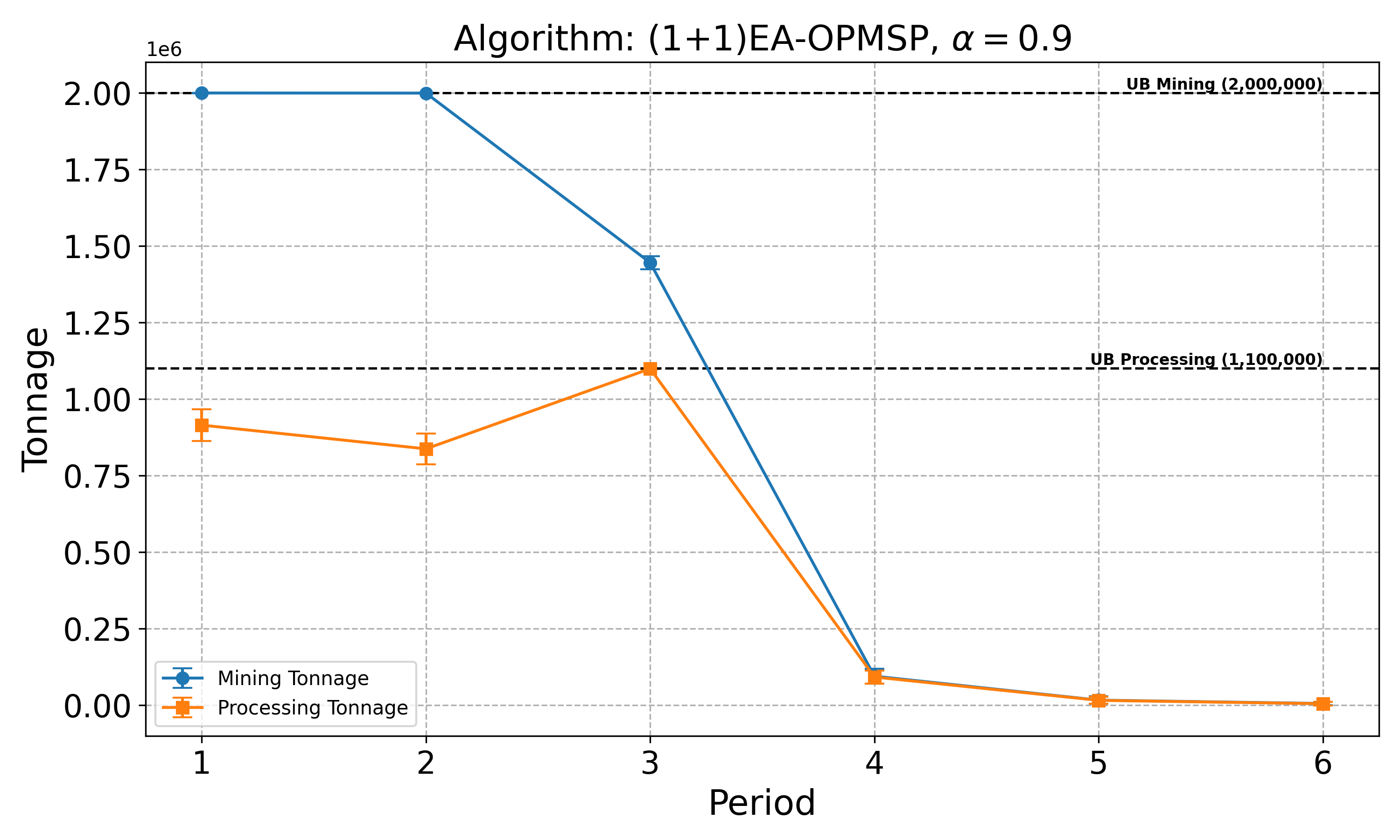
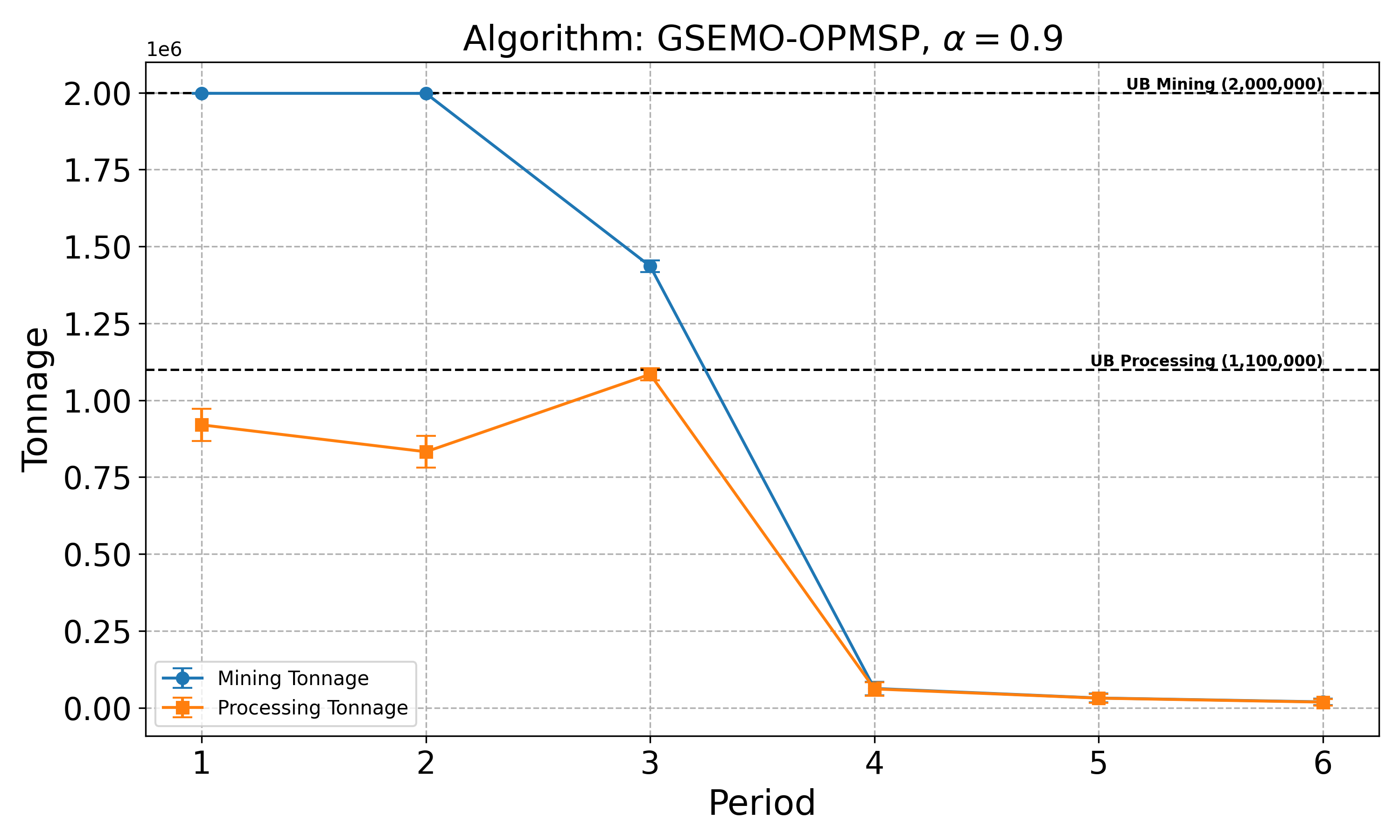
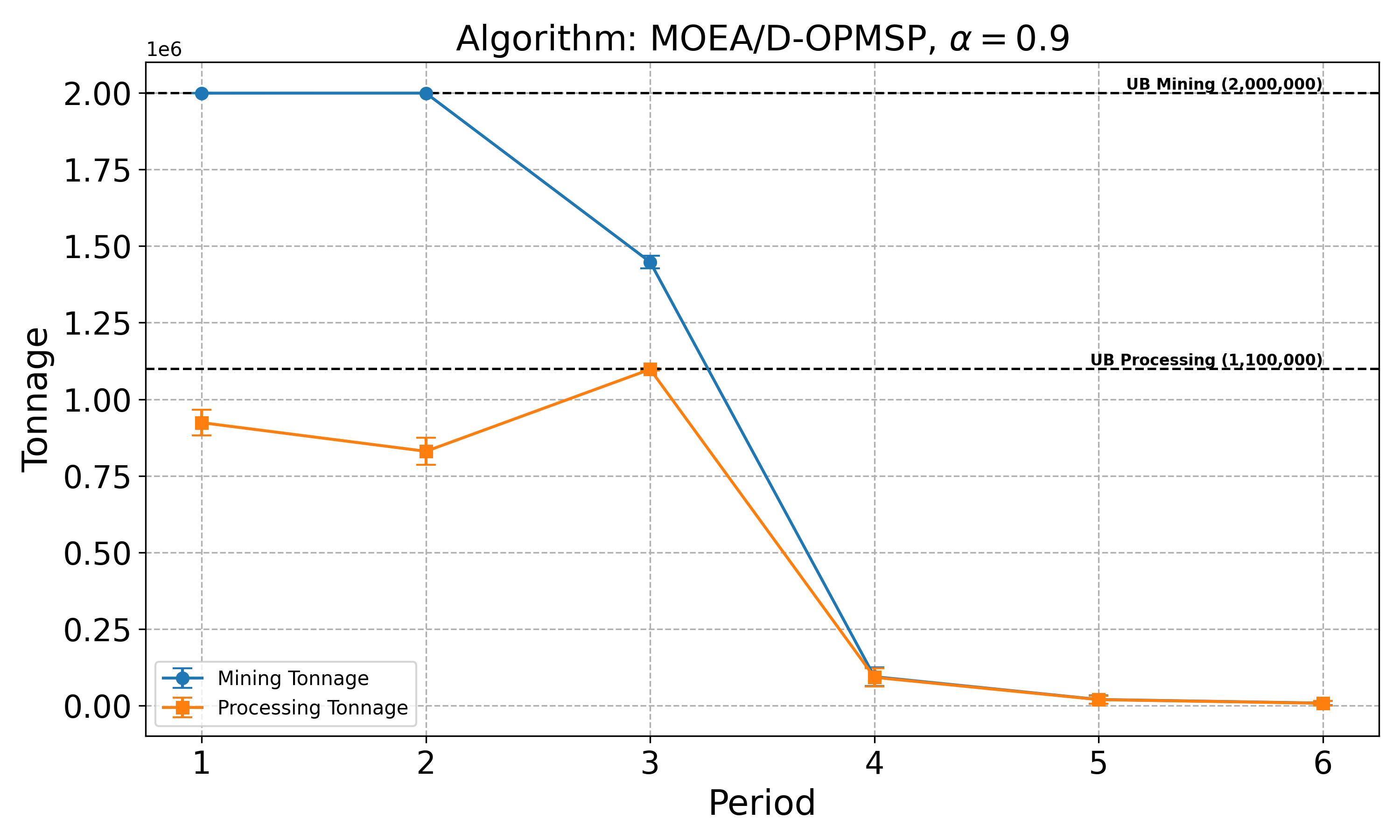
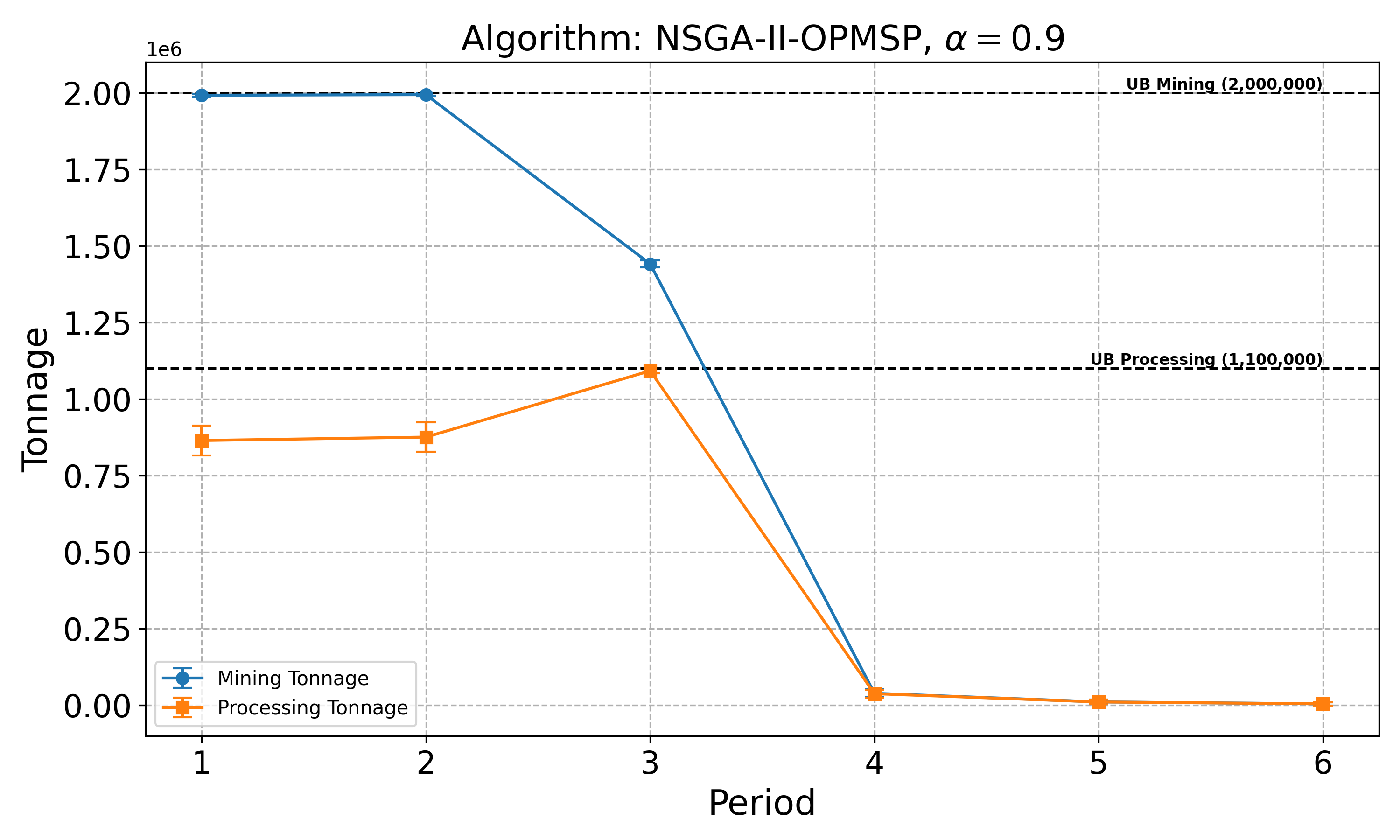
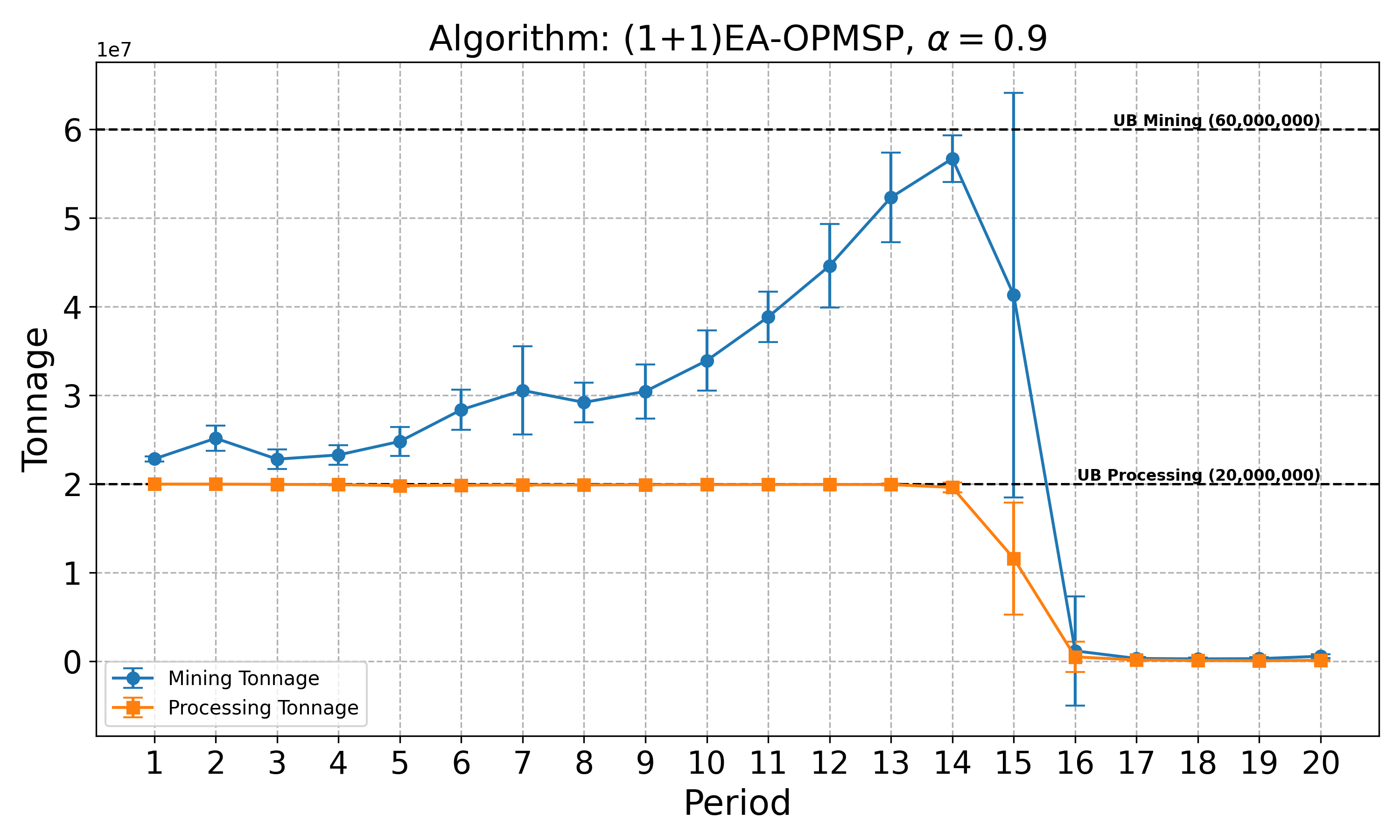
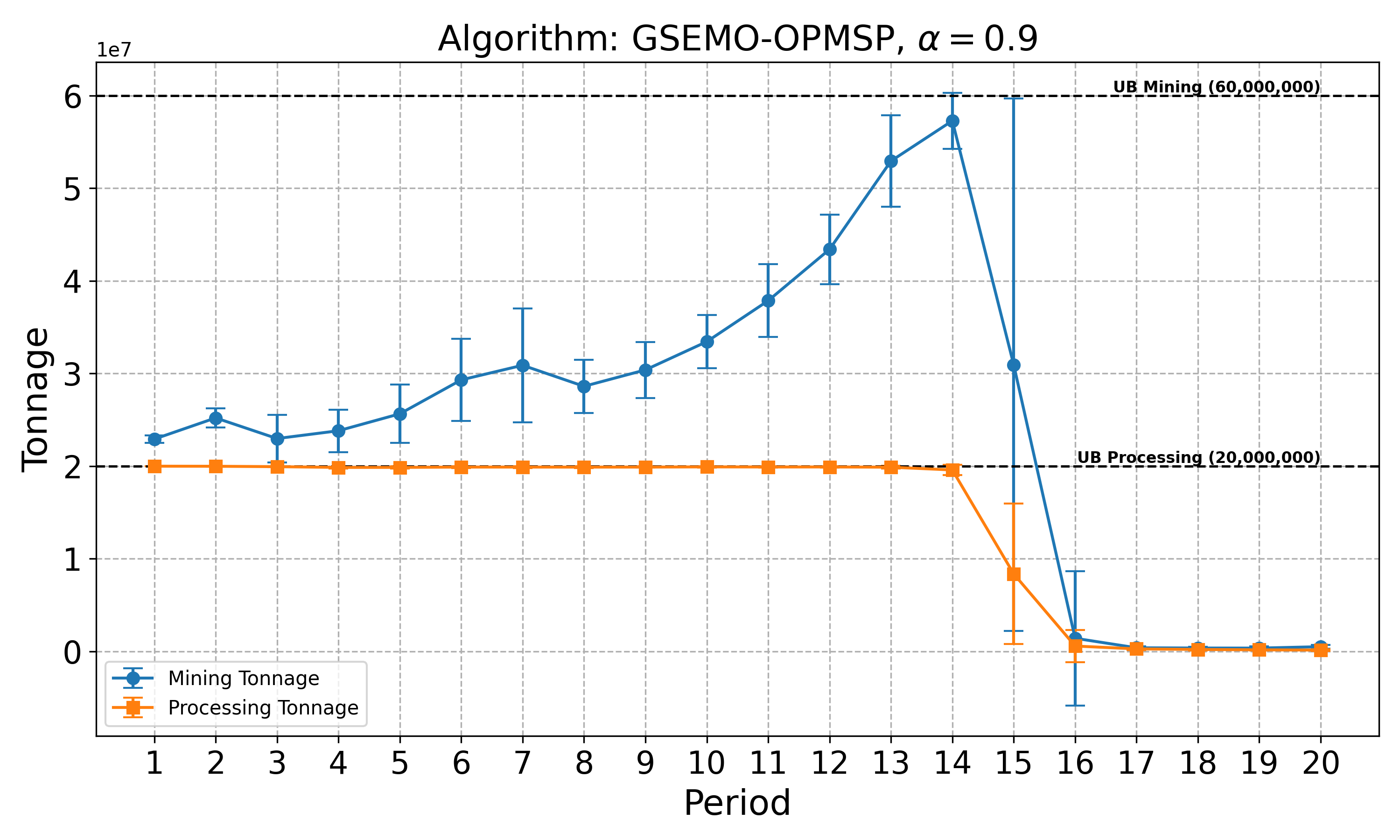
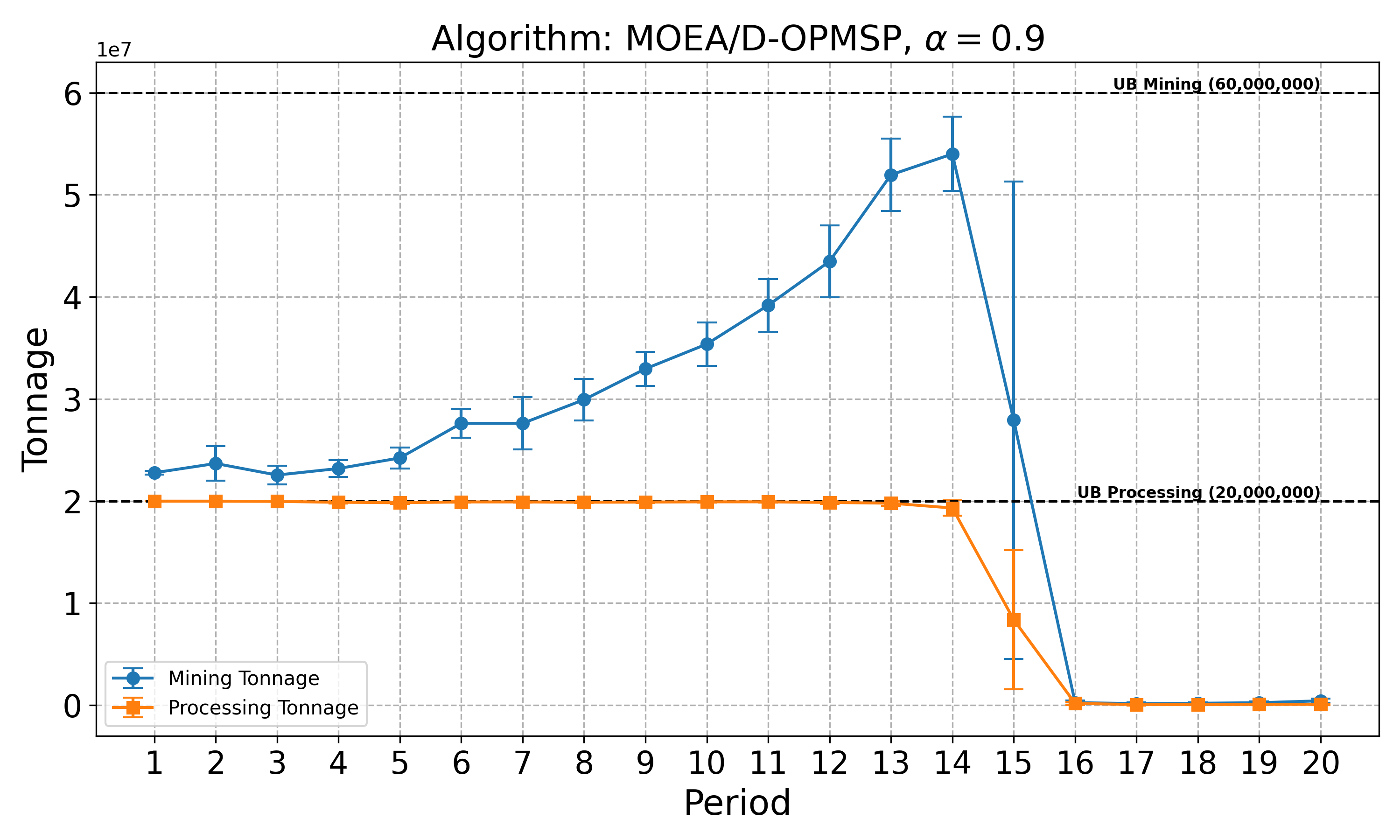
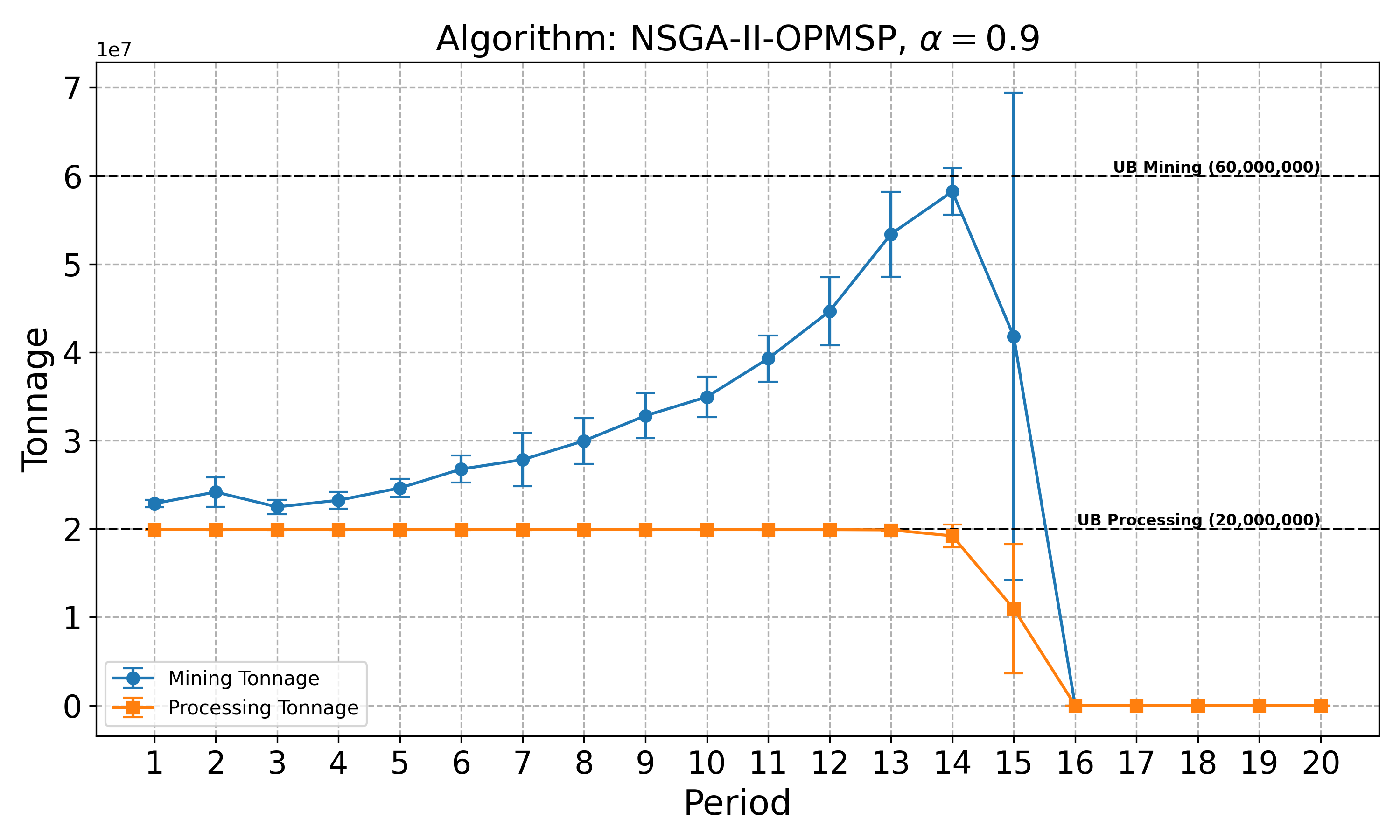
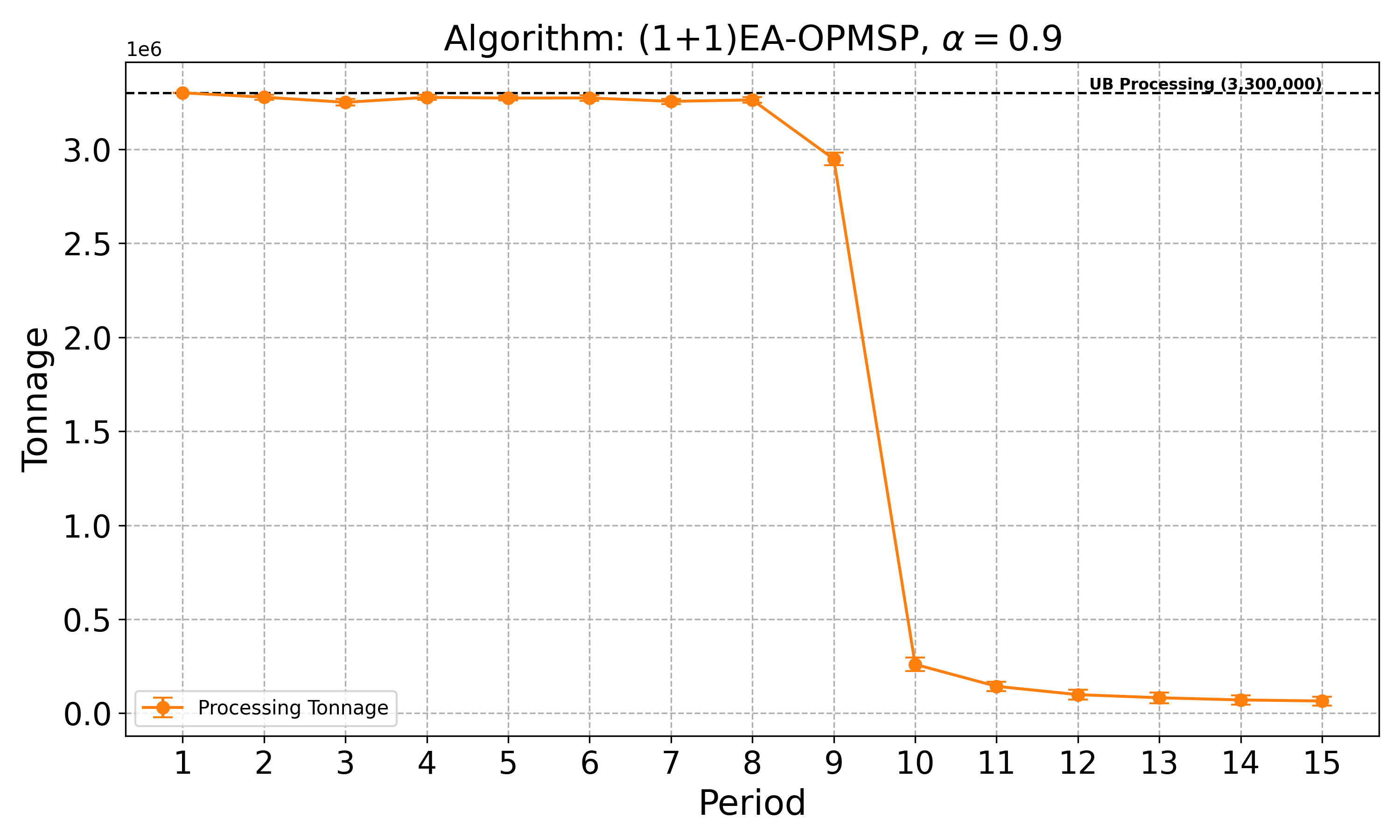
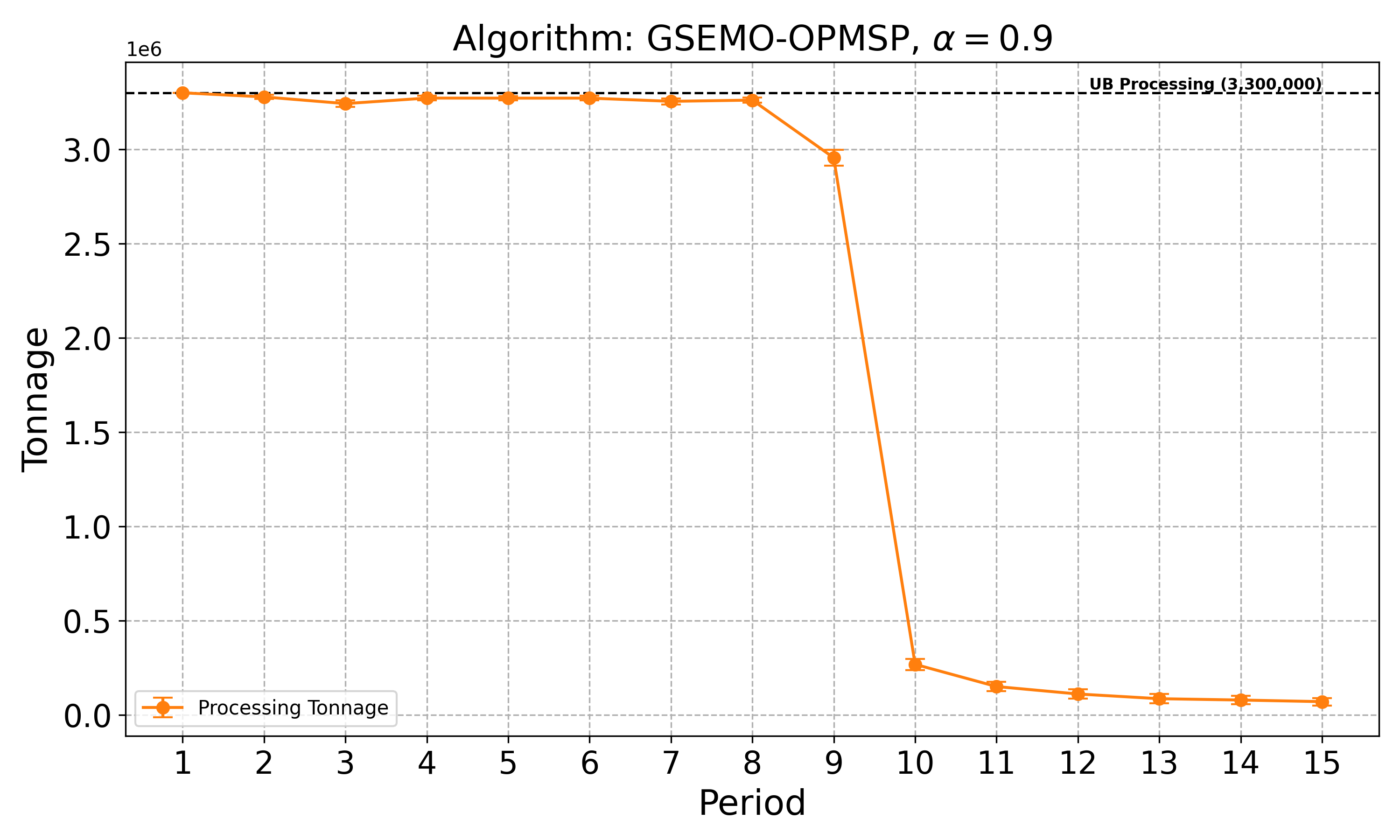
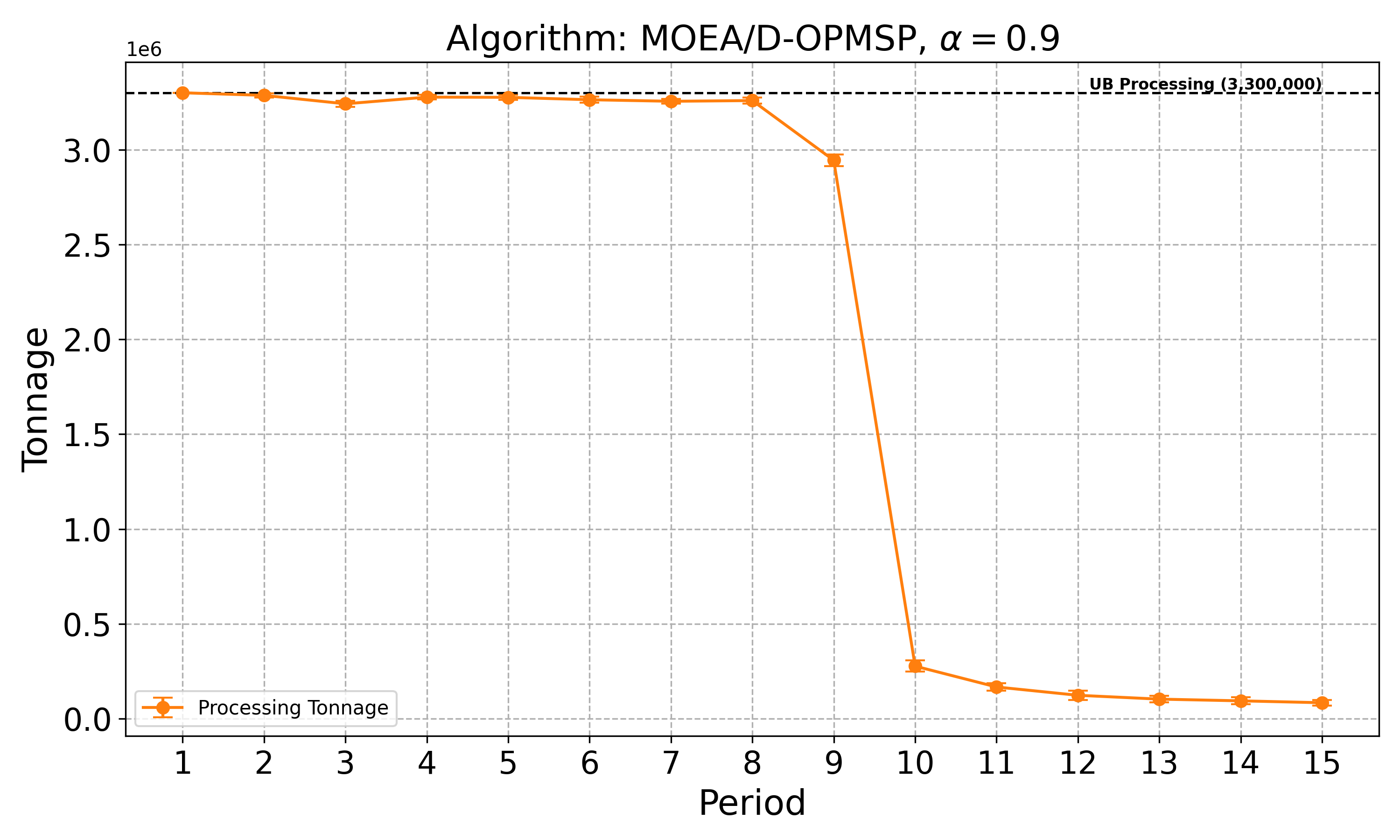
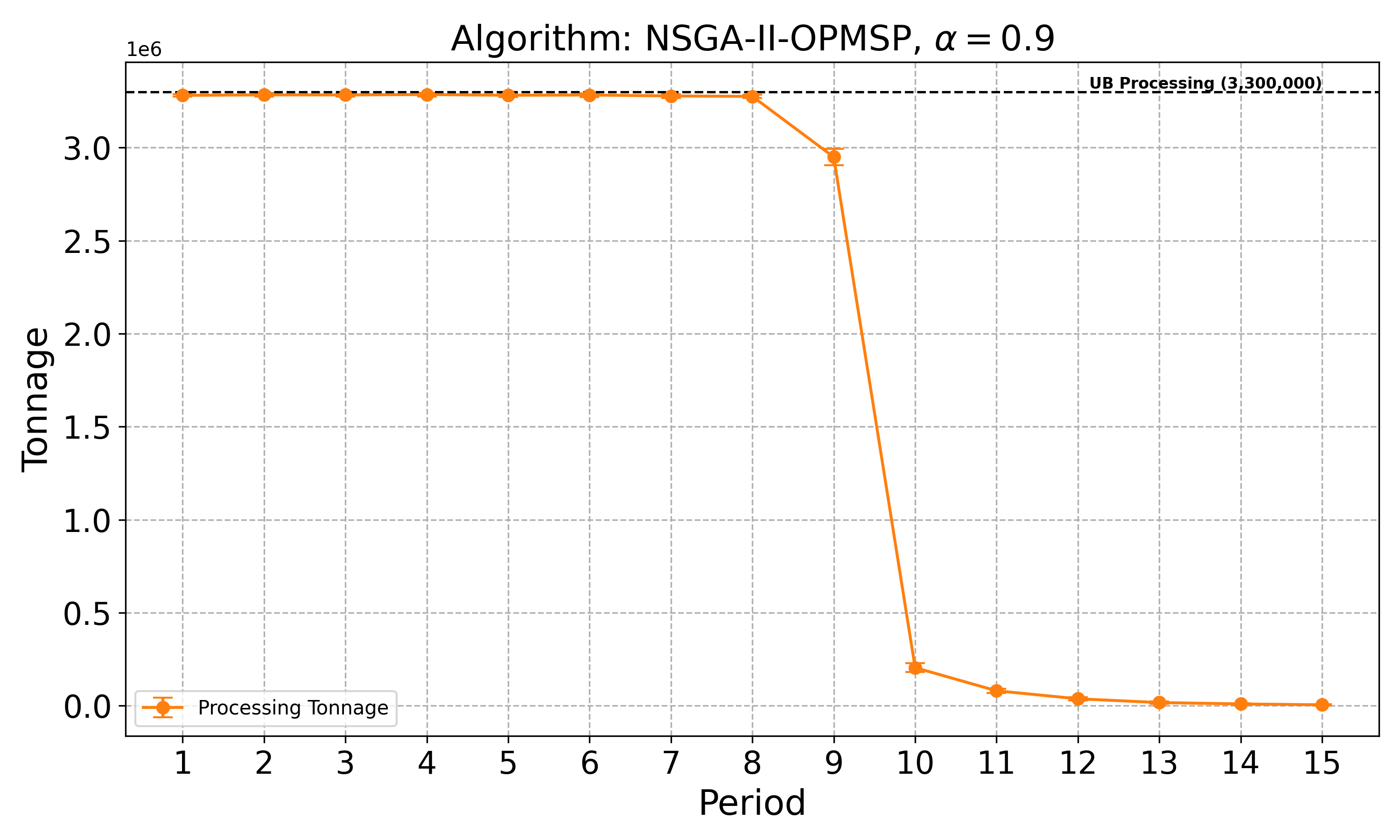
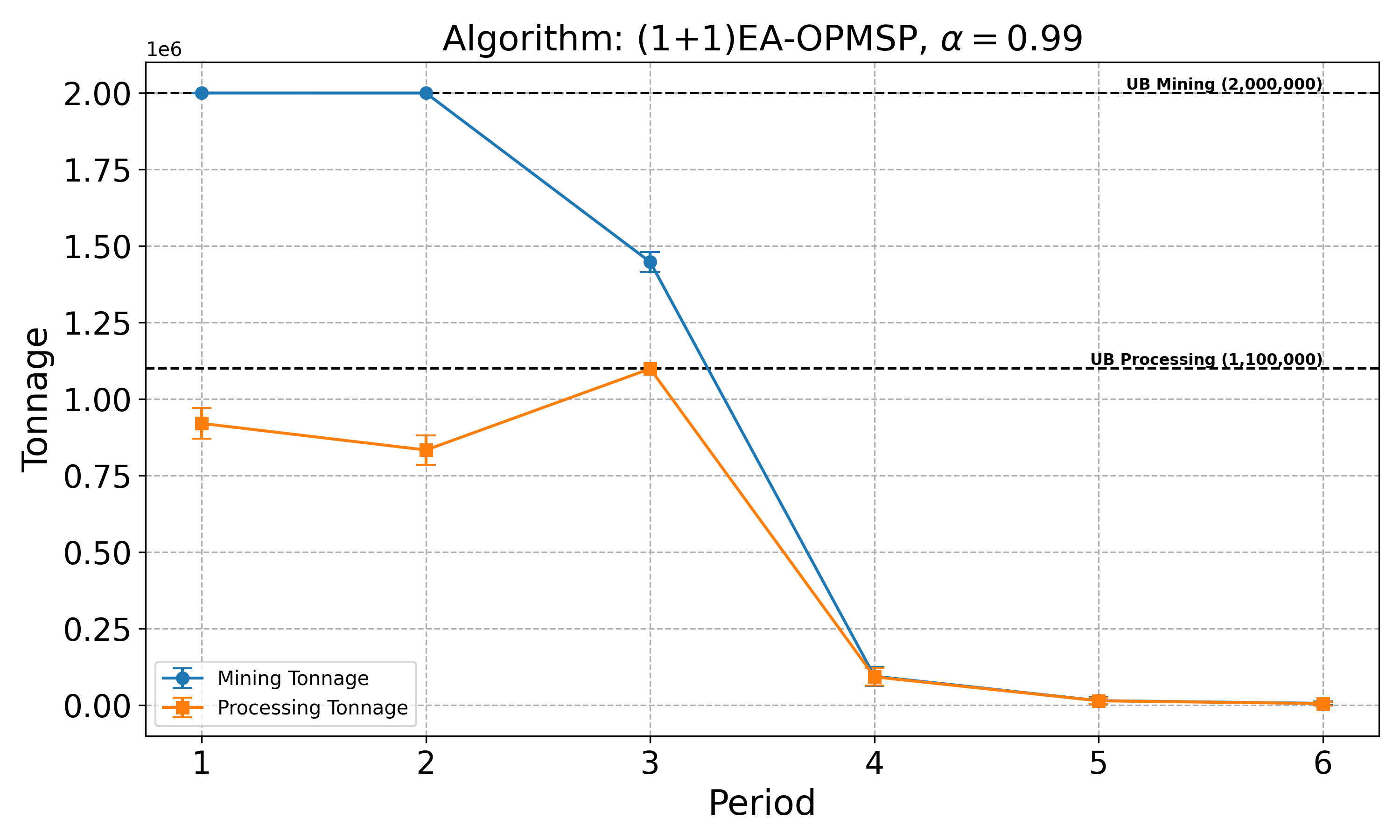
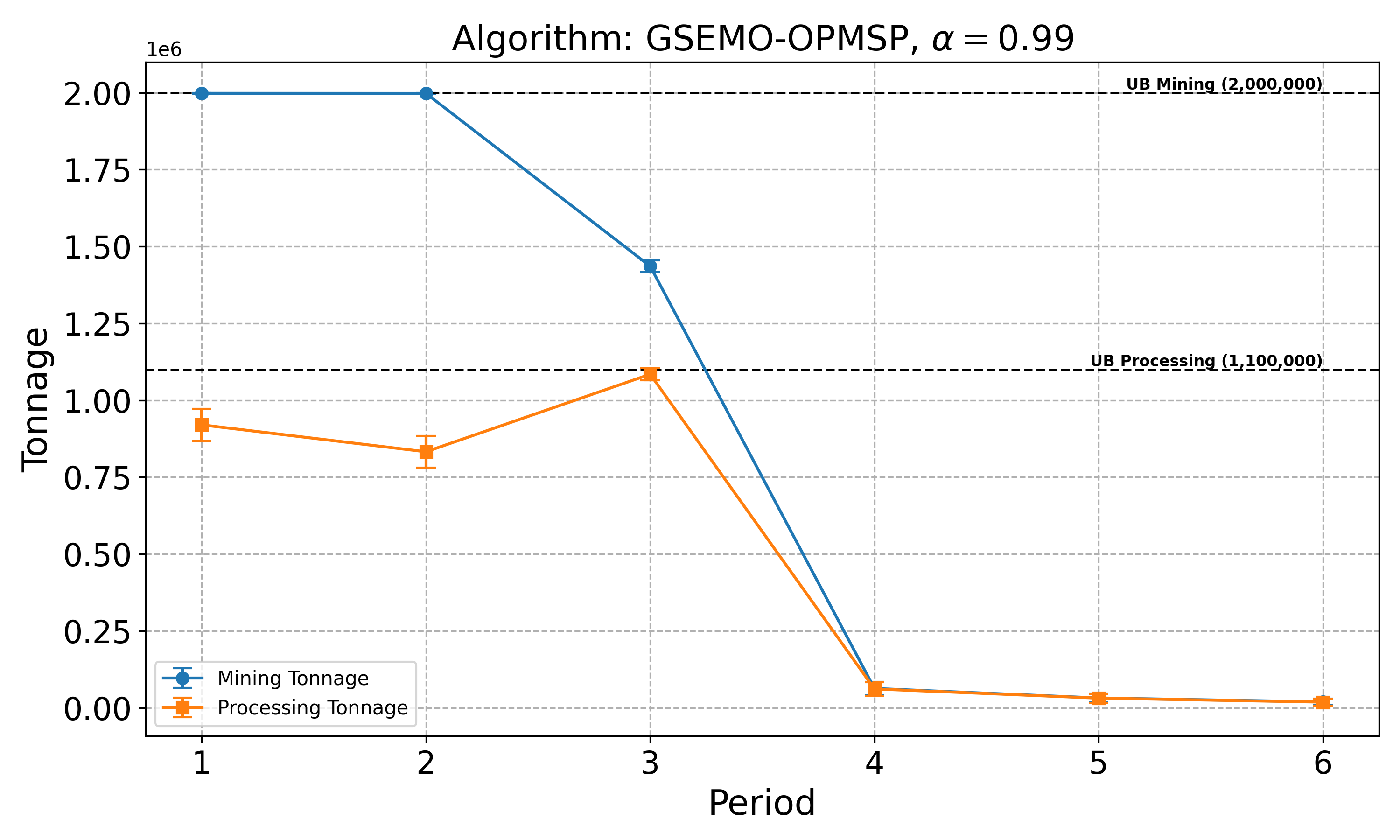
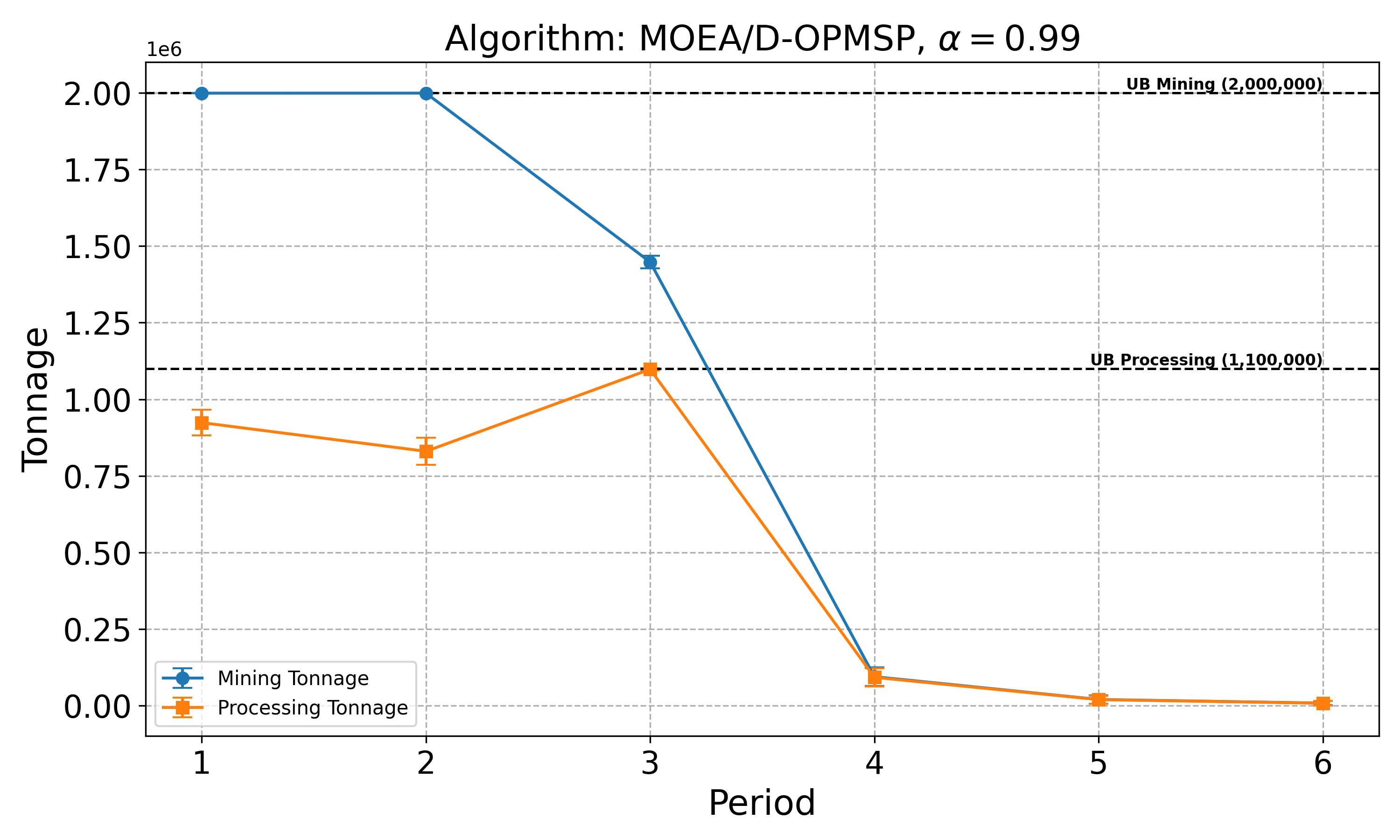
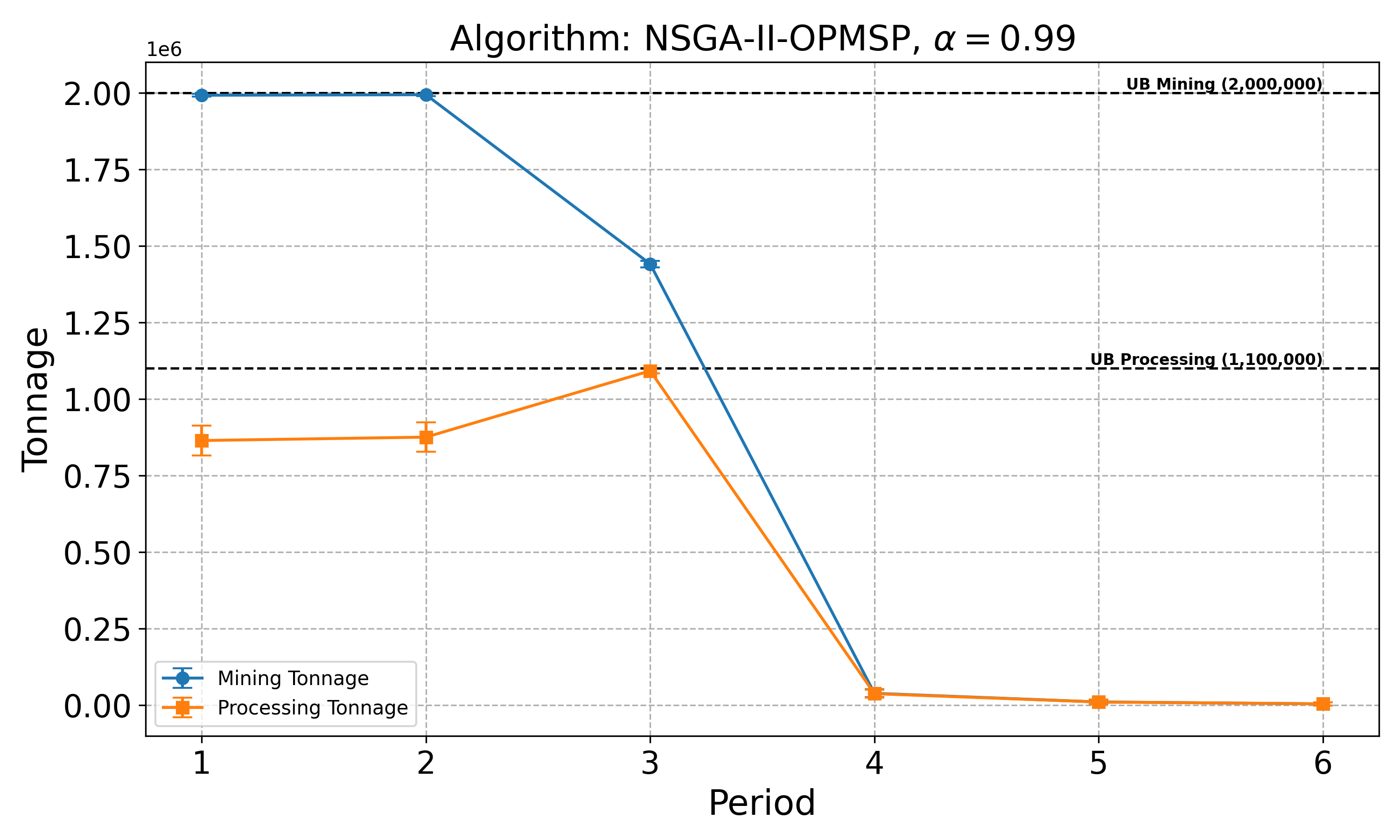
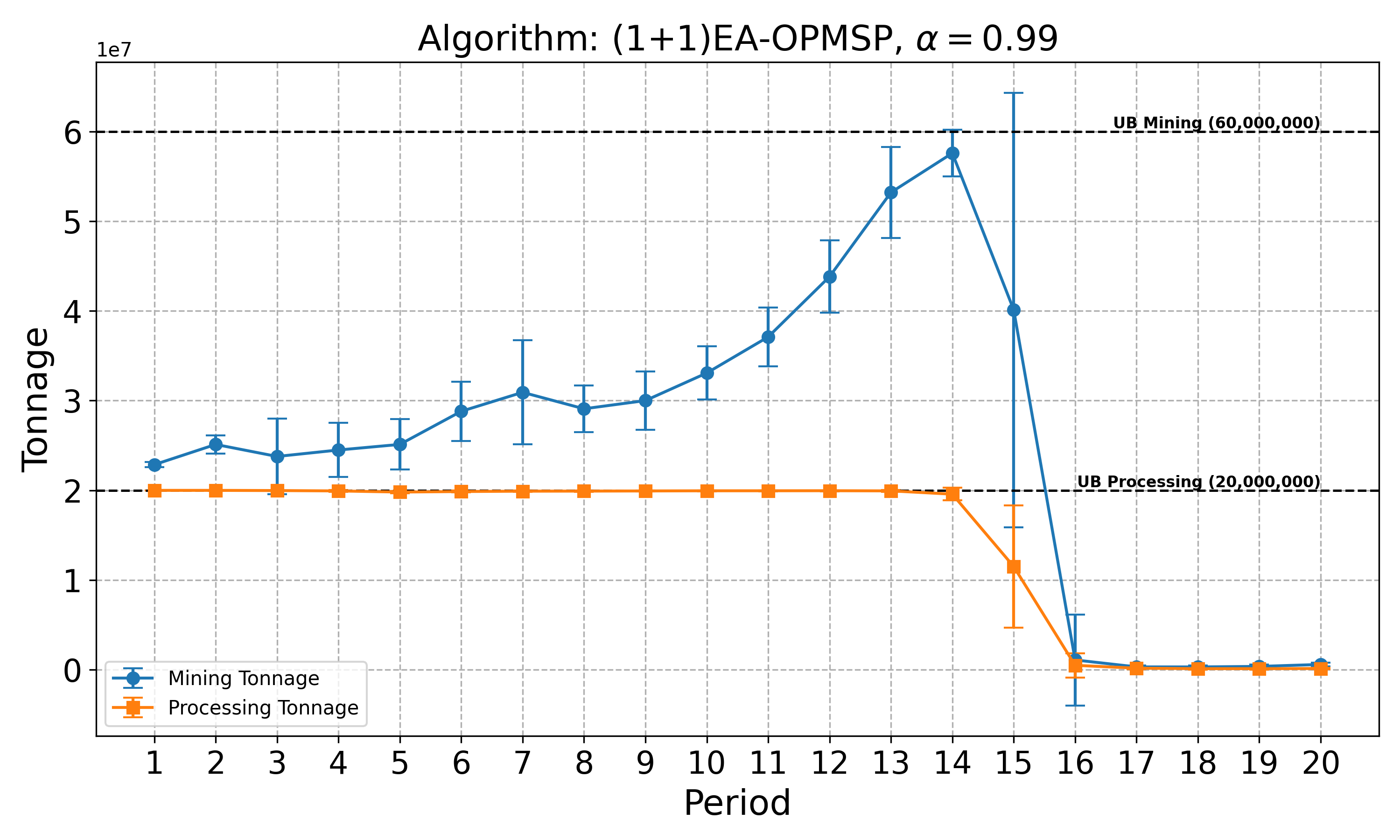
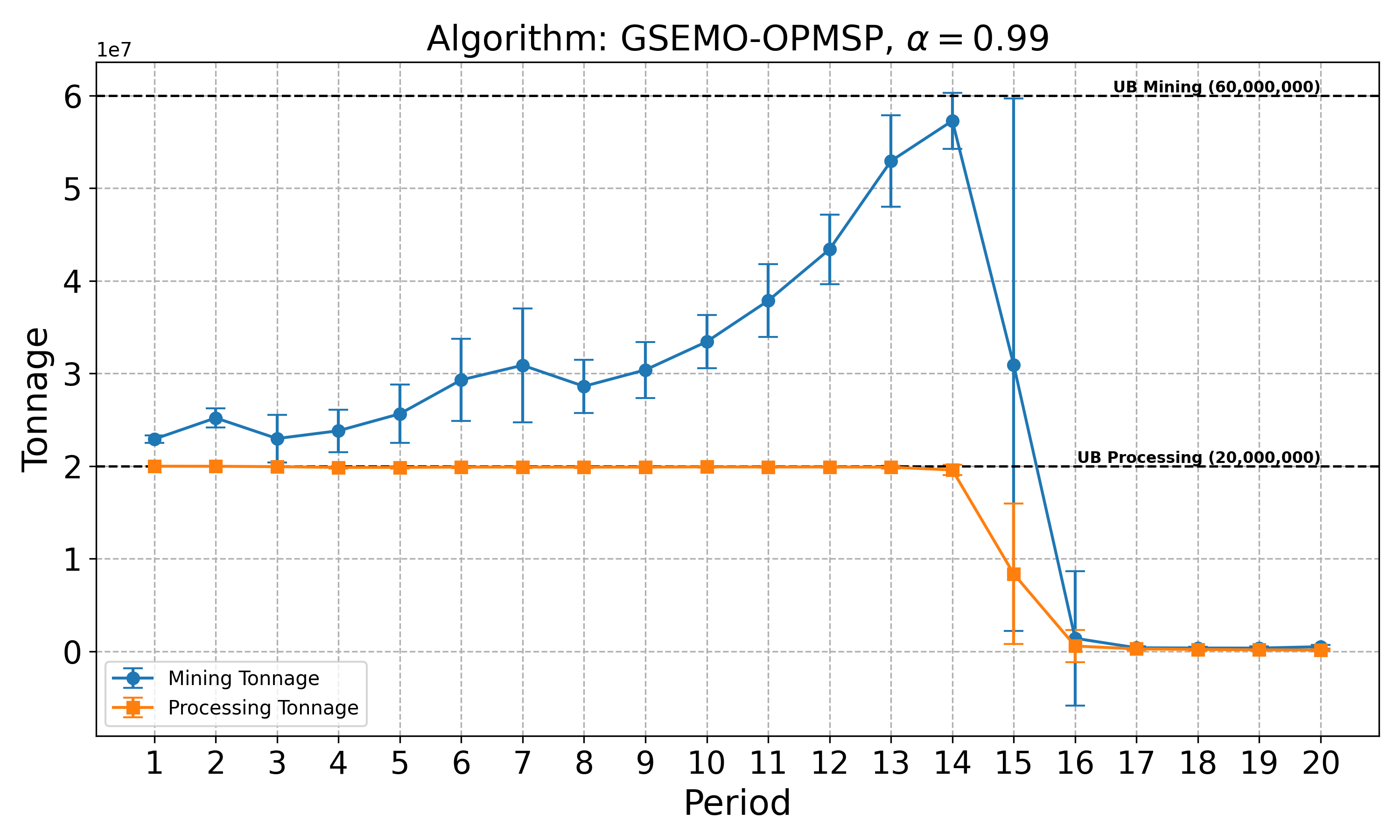
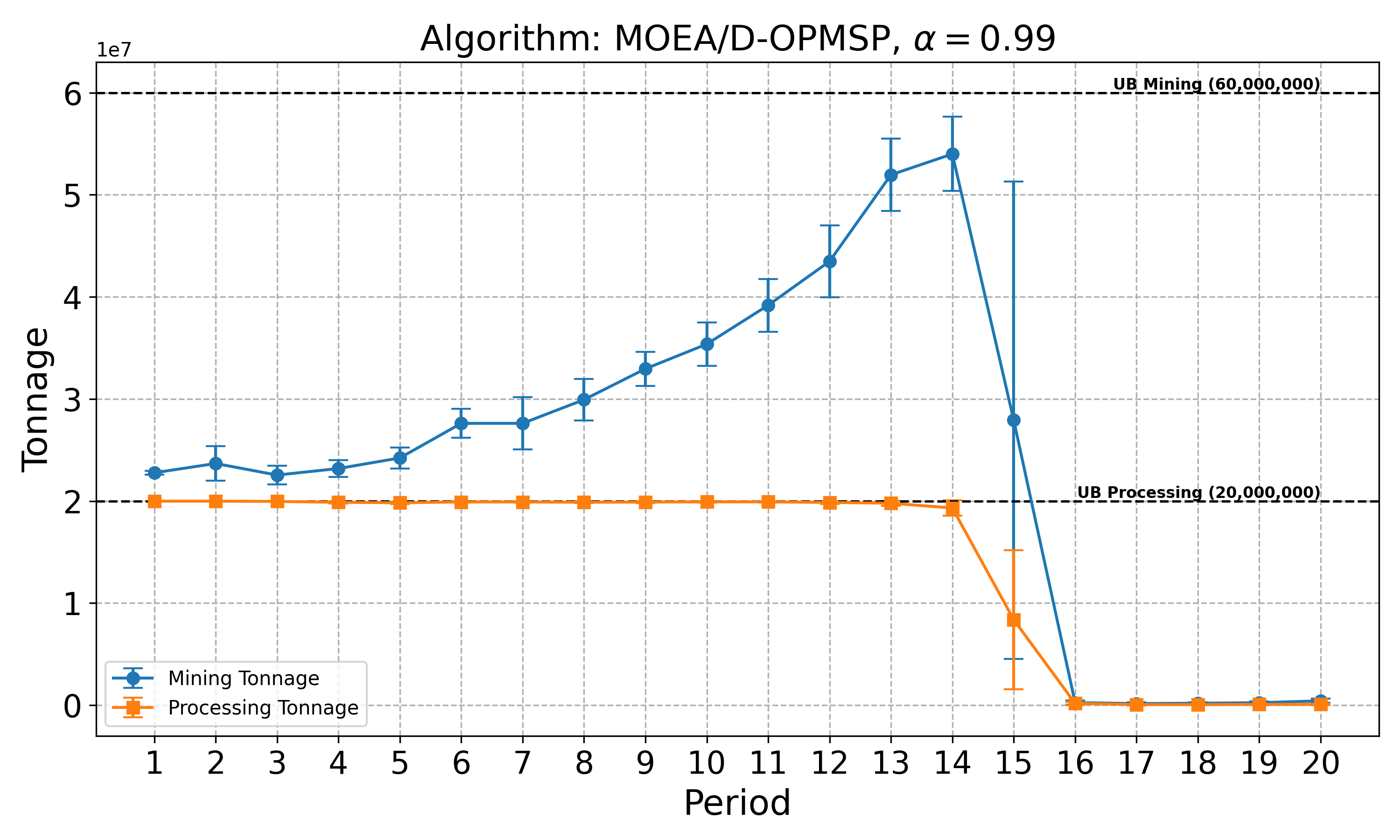
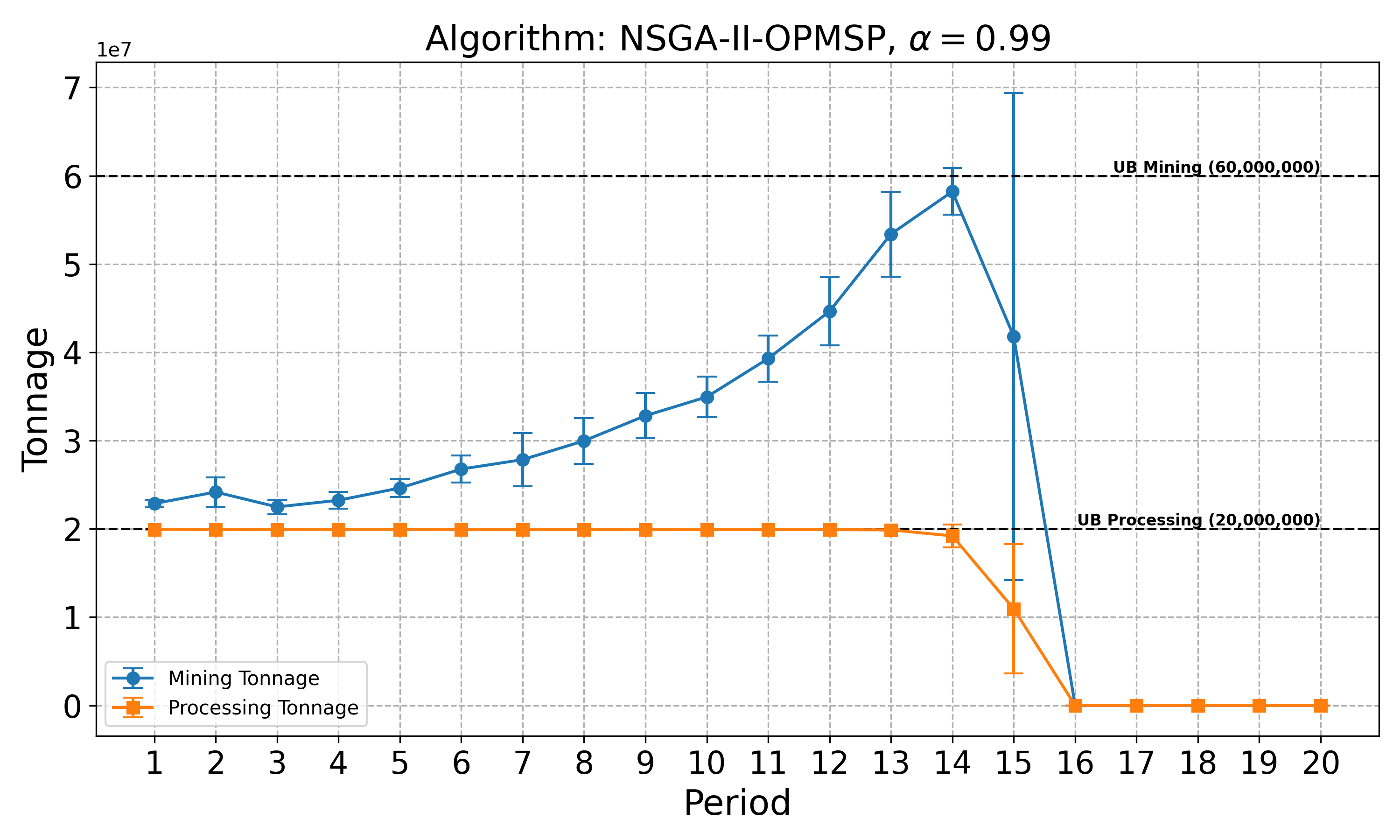
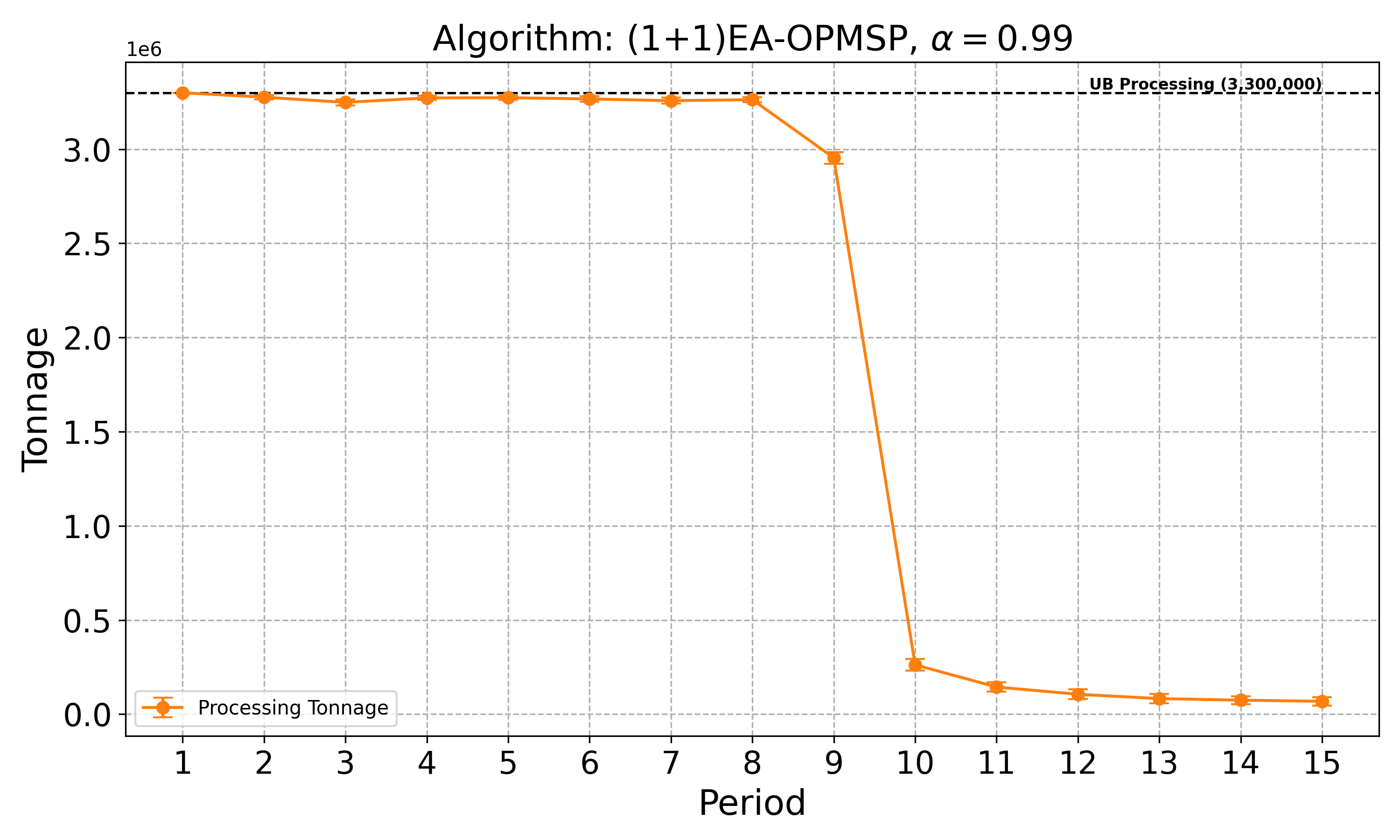
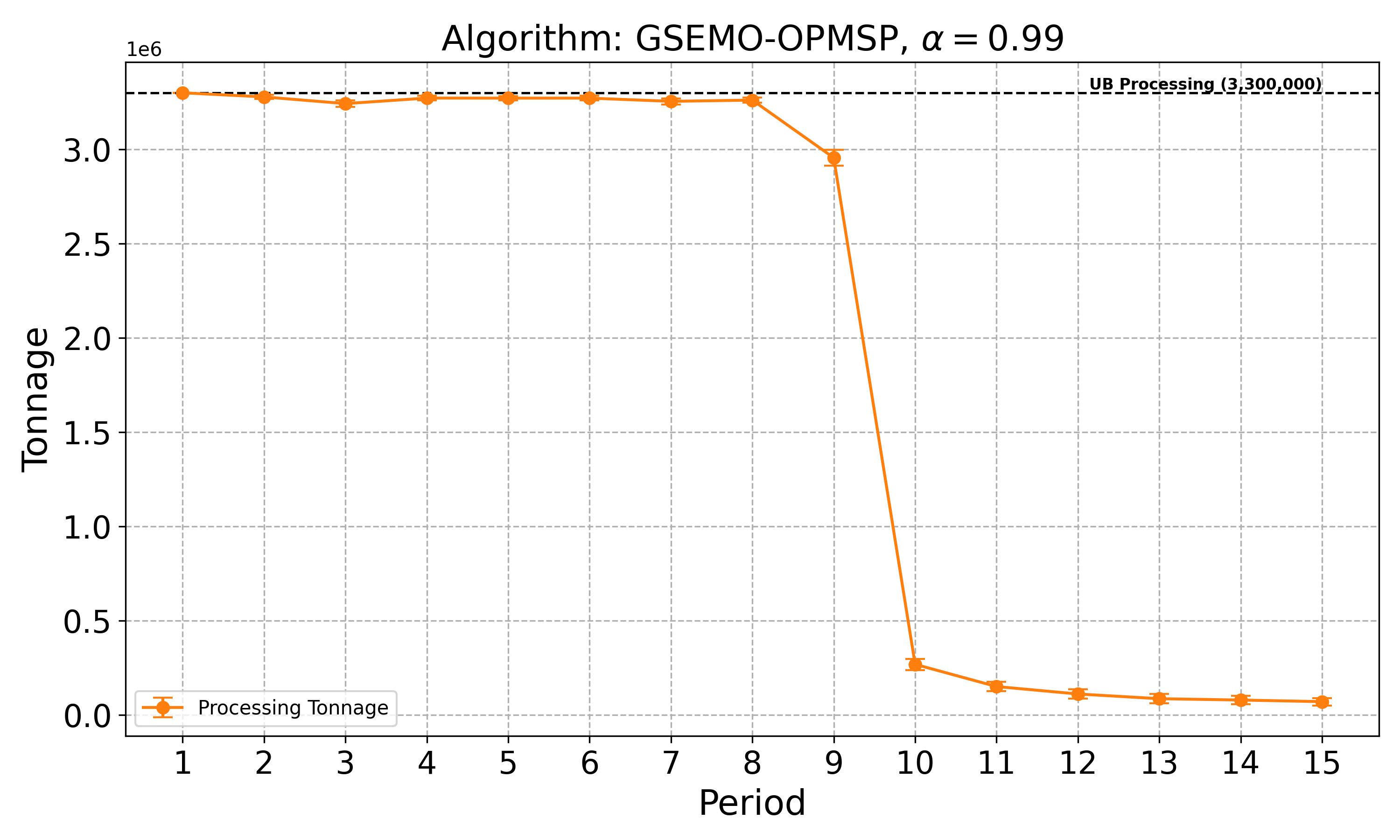
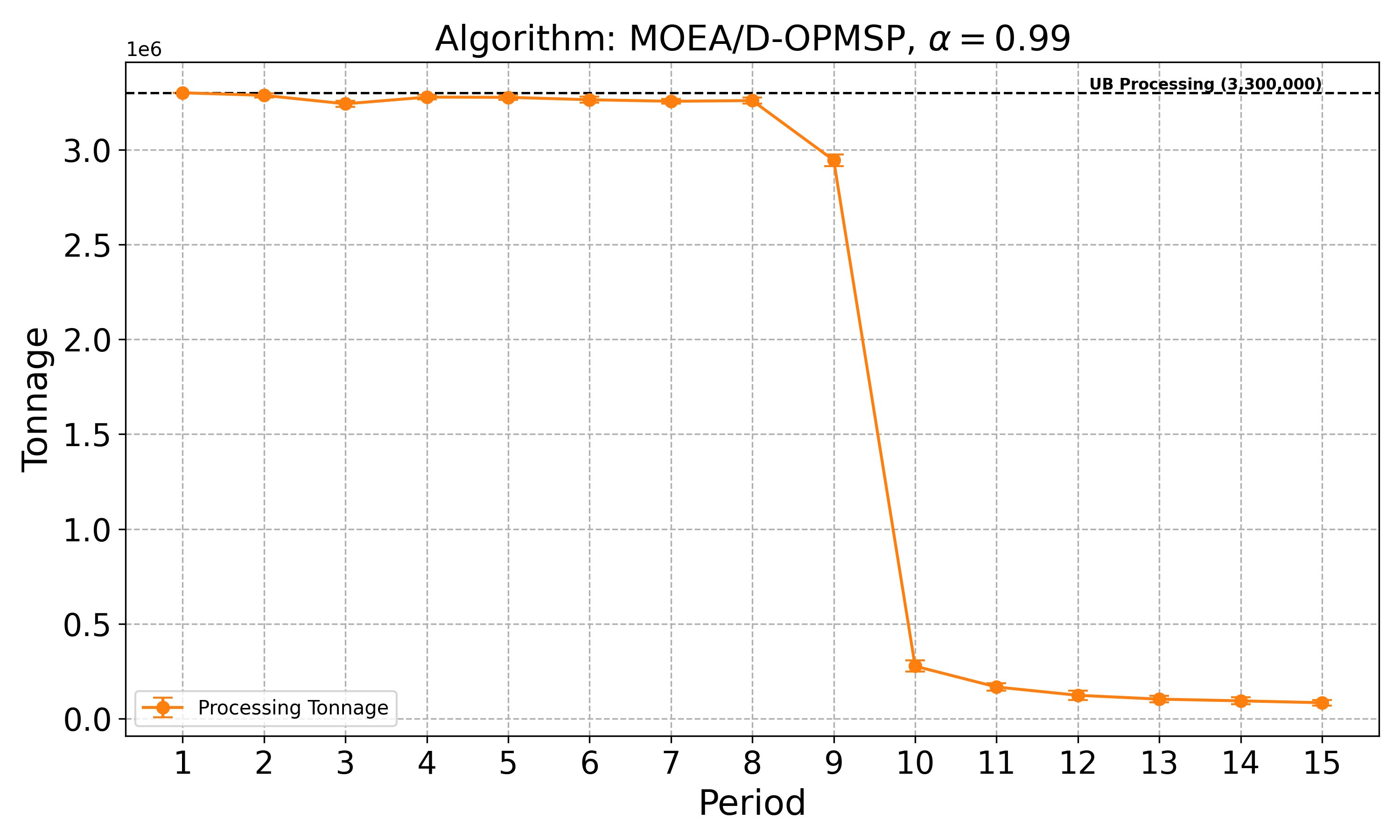
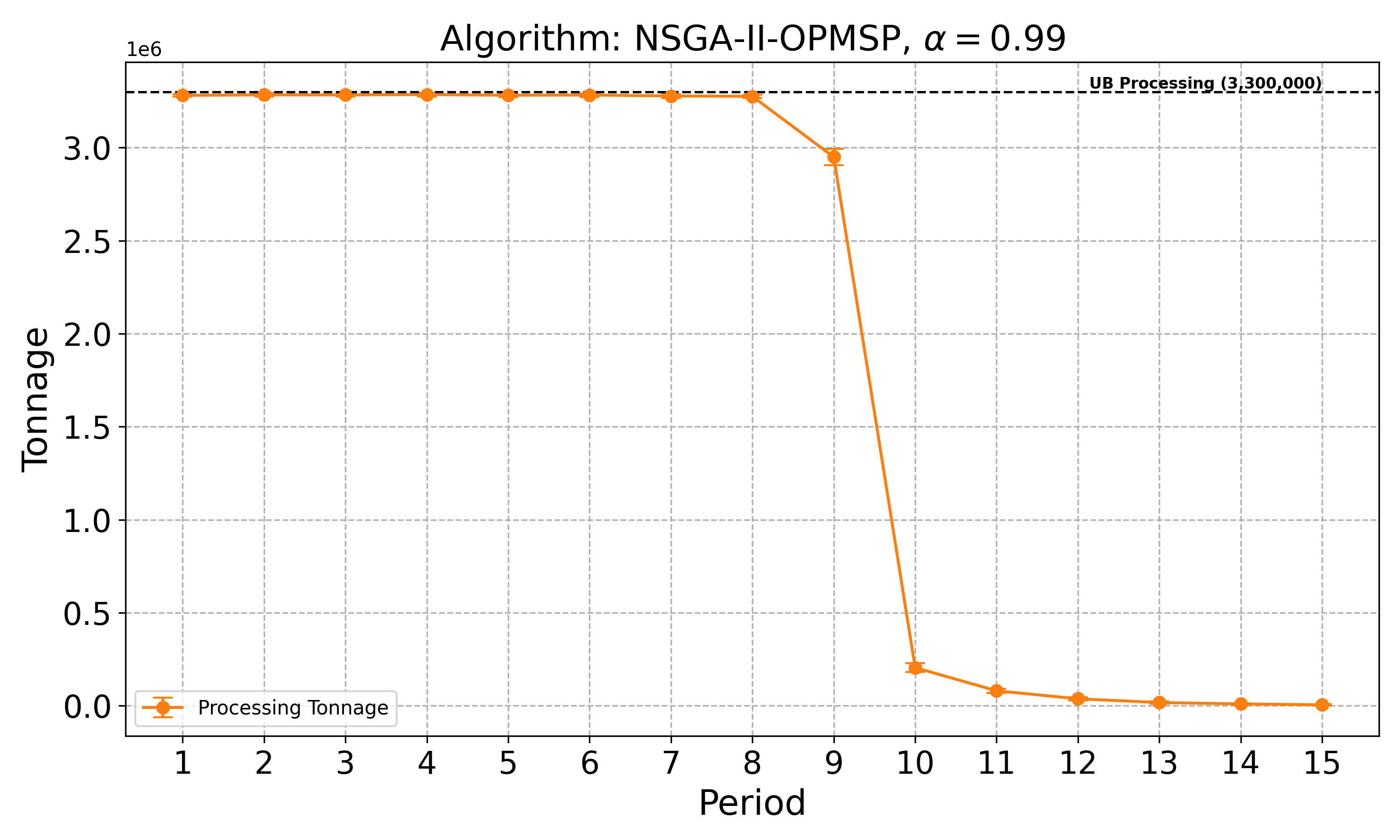
The open-pit mine scheduling problem (OPMSP) is a complex, computationally expensive process in long-term mine planning, constrained by operational and geological dependencies. Traditional deterministic approaches often ignore geological uncertainty, leading to suboptimal and potentially infeasible production schedules. Chance constraints allow modeling of stochastic components by ensuring probabilistic constraints are satisfied with high probability. This paper presents a bi-objective formulation of the OPMSP that simultaneously maximizes expected net present value and minimizes scheduling risk, independent of the confidence level required for the constraint. Solutions are represented using integer encoding, inherently satisfying reserve constraints. We introduce a domain-specific greedy randomized initialization and a precedence-aware period-swap mutation operator. We integrate these operators into three multi-objective evolutionary algorithms: the global simple evolutionary multi-objective optimizer (GSEMO), a mutation-only variant of multi-objective evolutionary algorithm based on decomposition (MOEA/D), and non-dominated sorting genetic algorithm II (NSGA-II). We compare our bi-objective formulation against the single-objective approach, which depends on a specific confidence level, by analyzing mine deposits consisting of up to 112 687 blocks. Results demonstrate that the proposed bi-objective formulation yields more robust and balanced trade-offs between economic value and risk compared to single-objective, confidence-dependent approach.