Post-Training LLMs as Better Decision-Making Agents: A Regret-Minimization Approach

📝 Original Info

• Title: Post-Training LLMs as Better Decision-Making Agents: A Regret-Minimization Approach
• ArXiv ID: 2511.04393
• Date: 2025-11-06
• Authors: Chanwoo Park, Ziyang Chen, Asuman Ozdaglar, Kaiqing Zhang

📝 Abstract

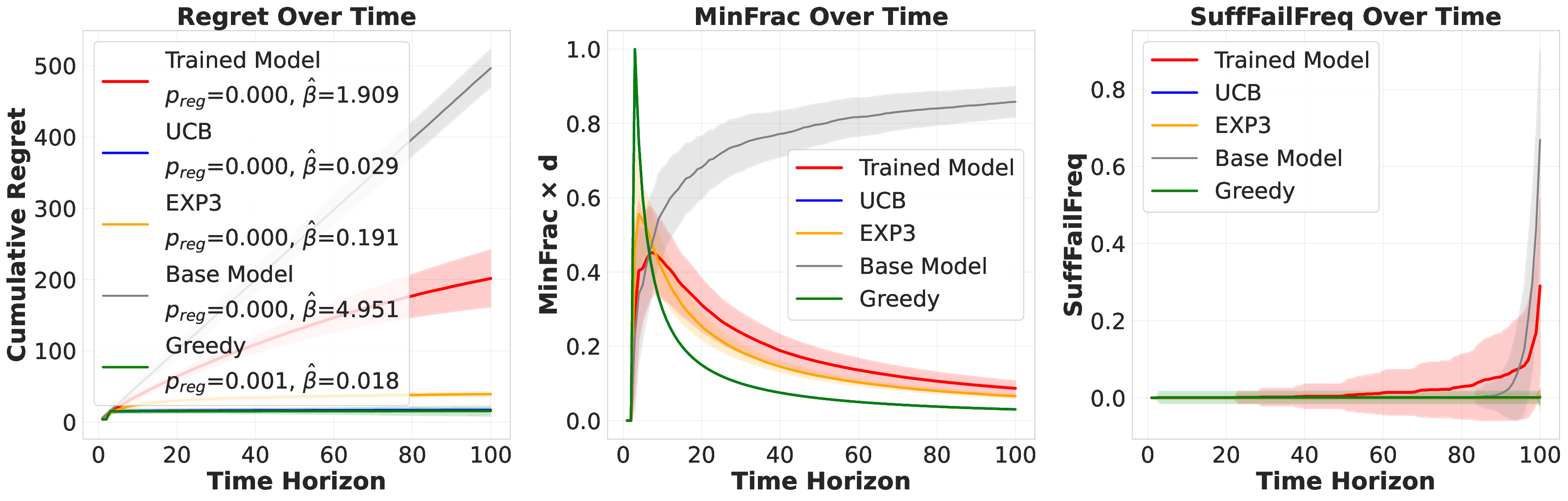
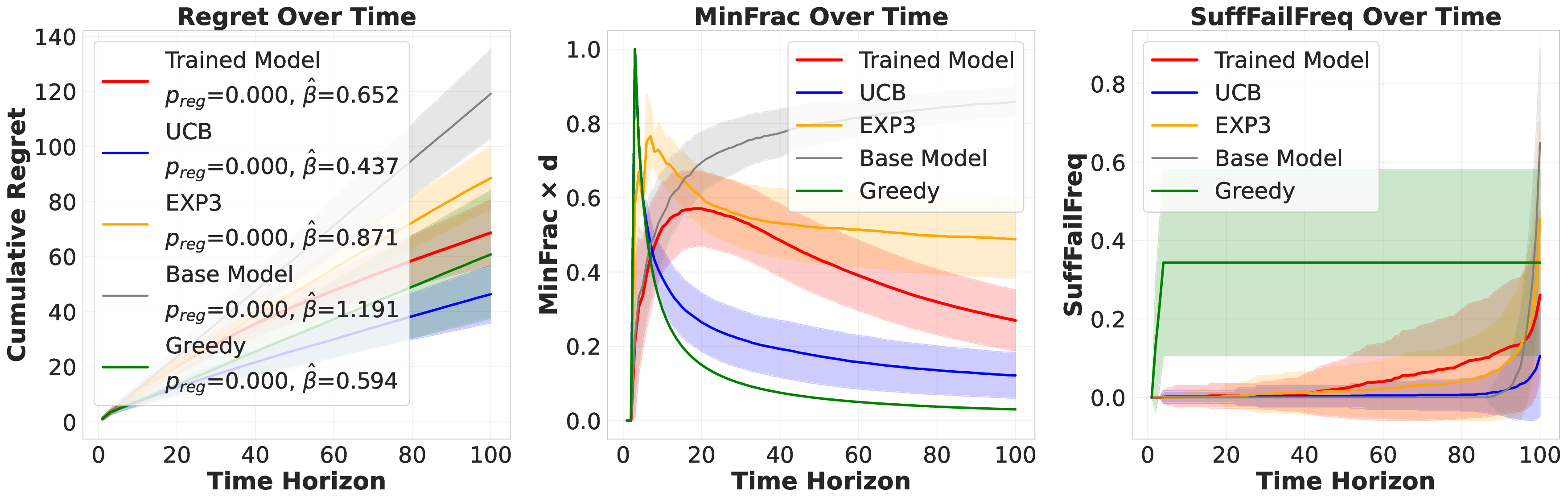
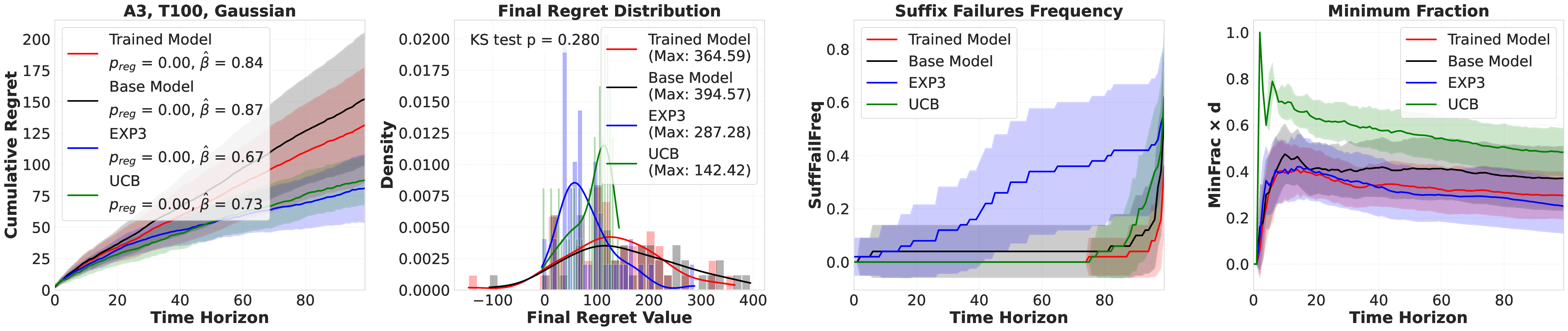
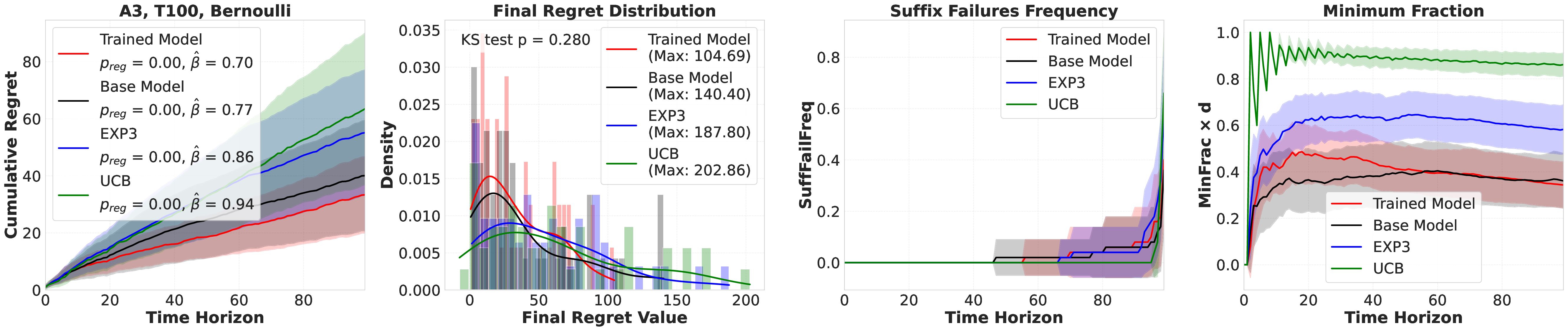
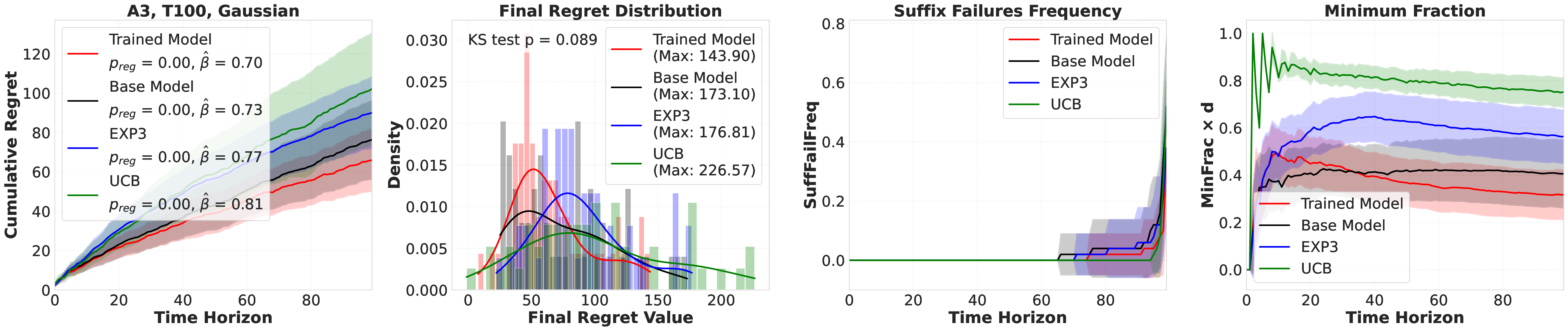
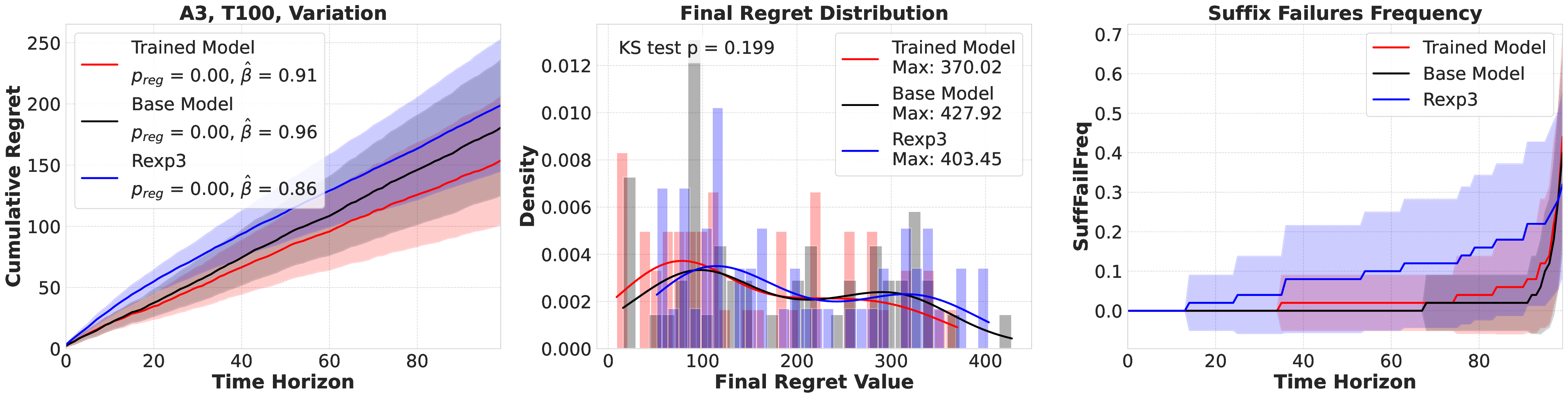
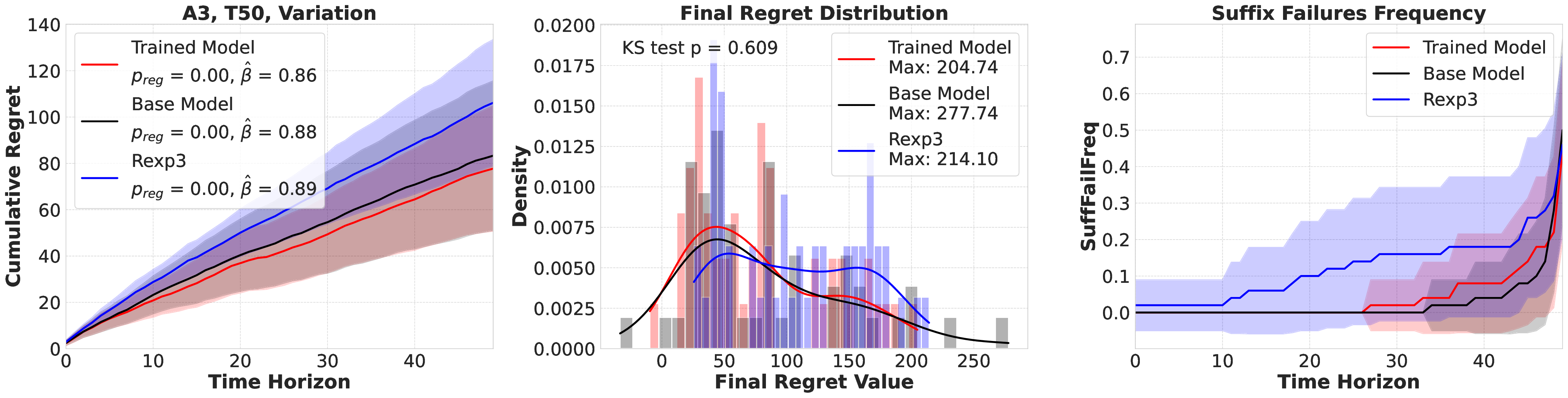
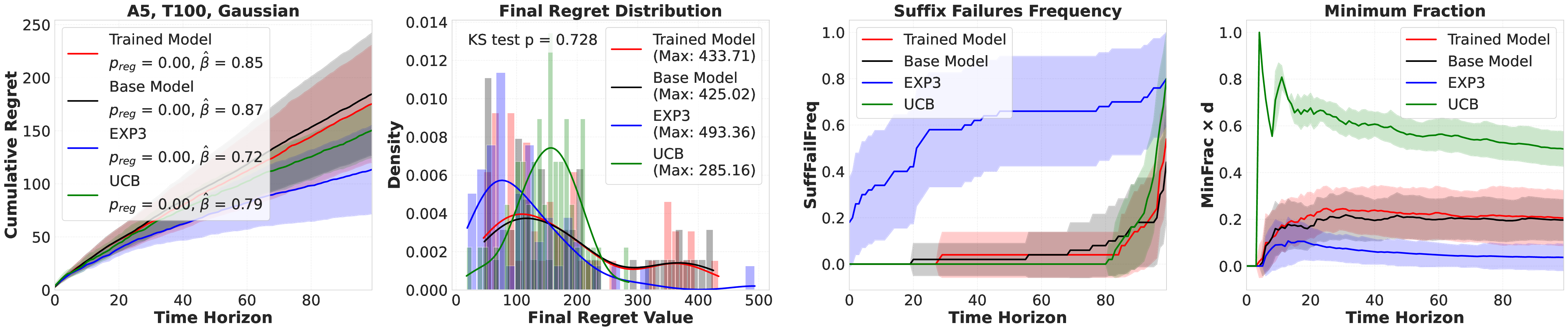
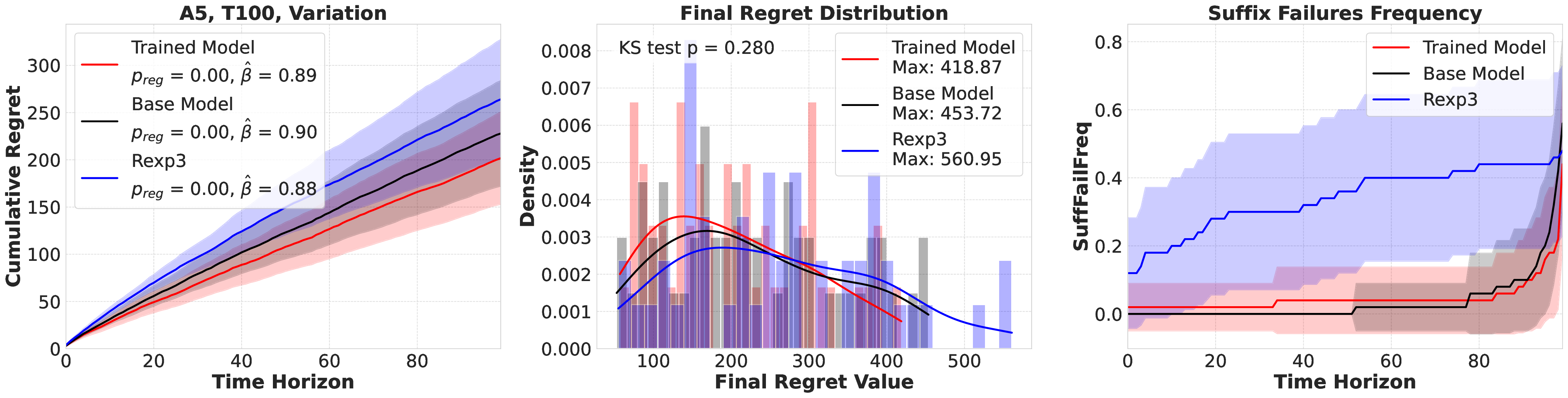
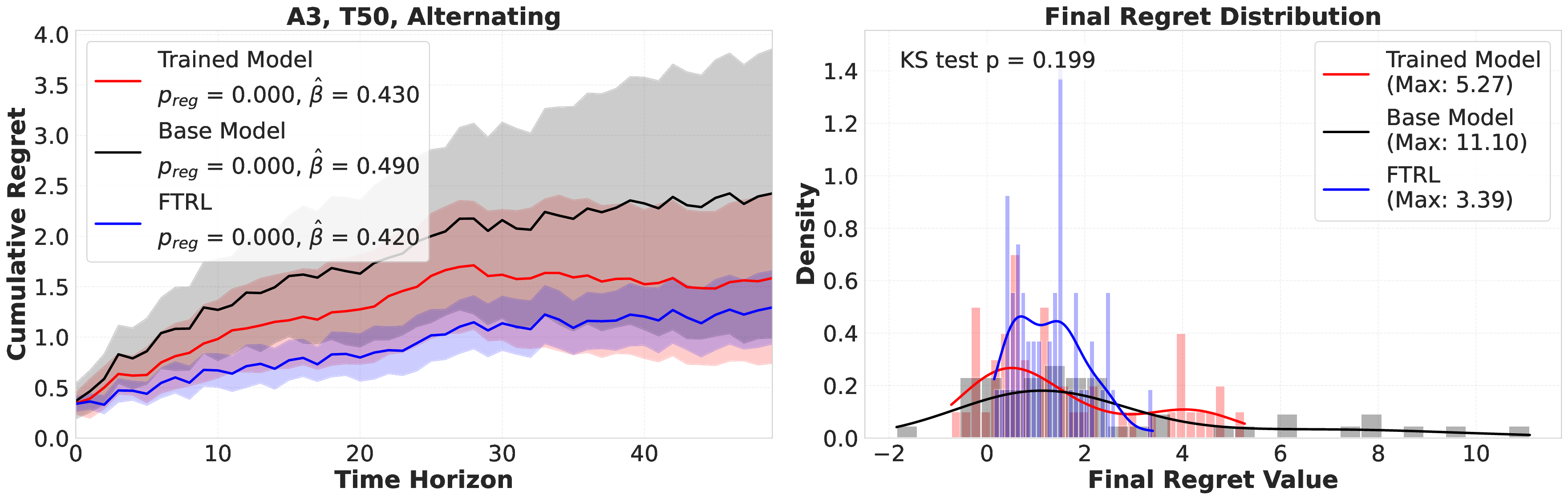
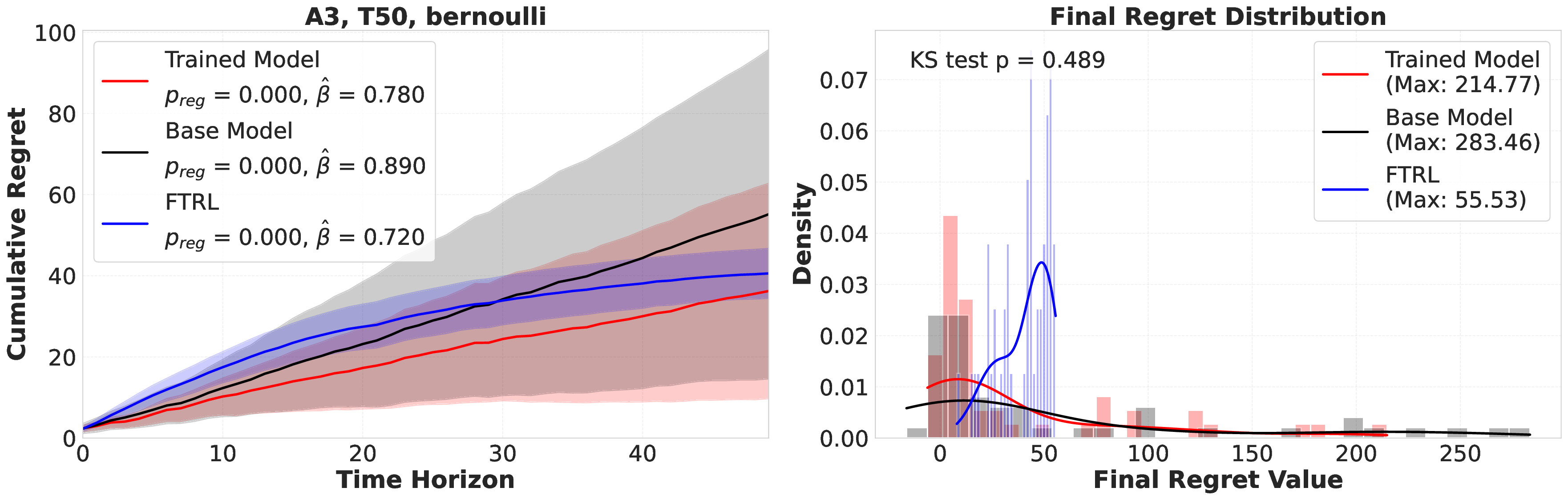
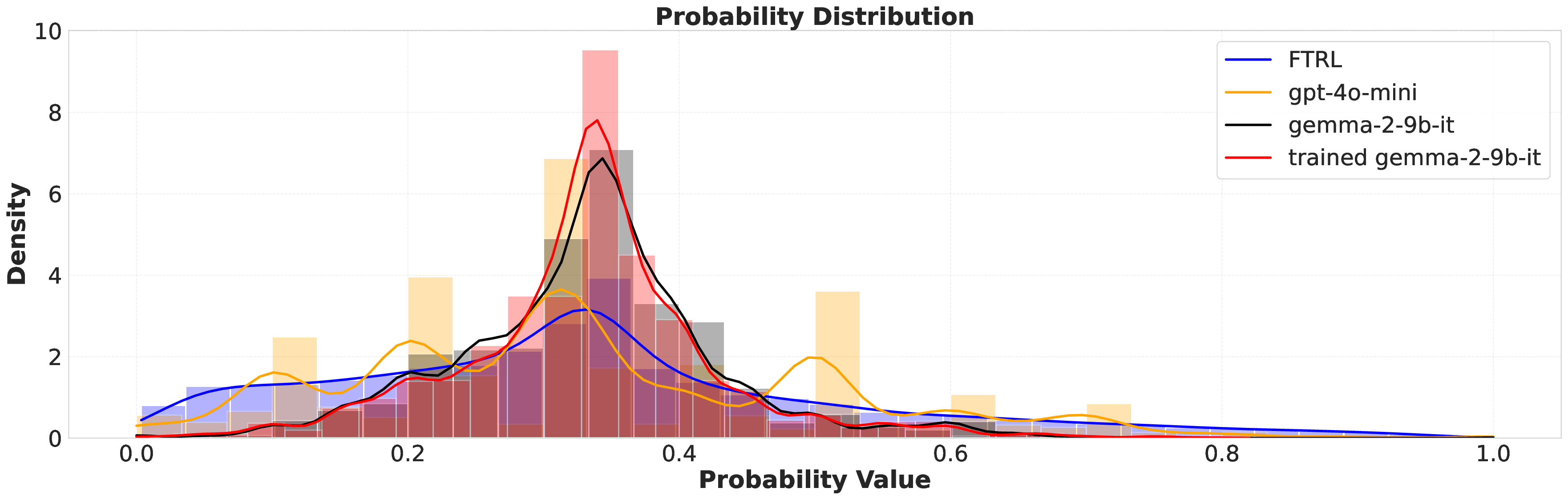
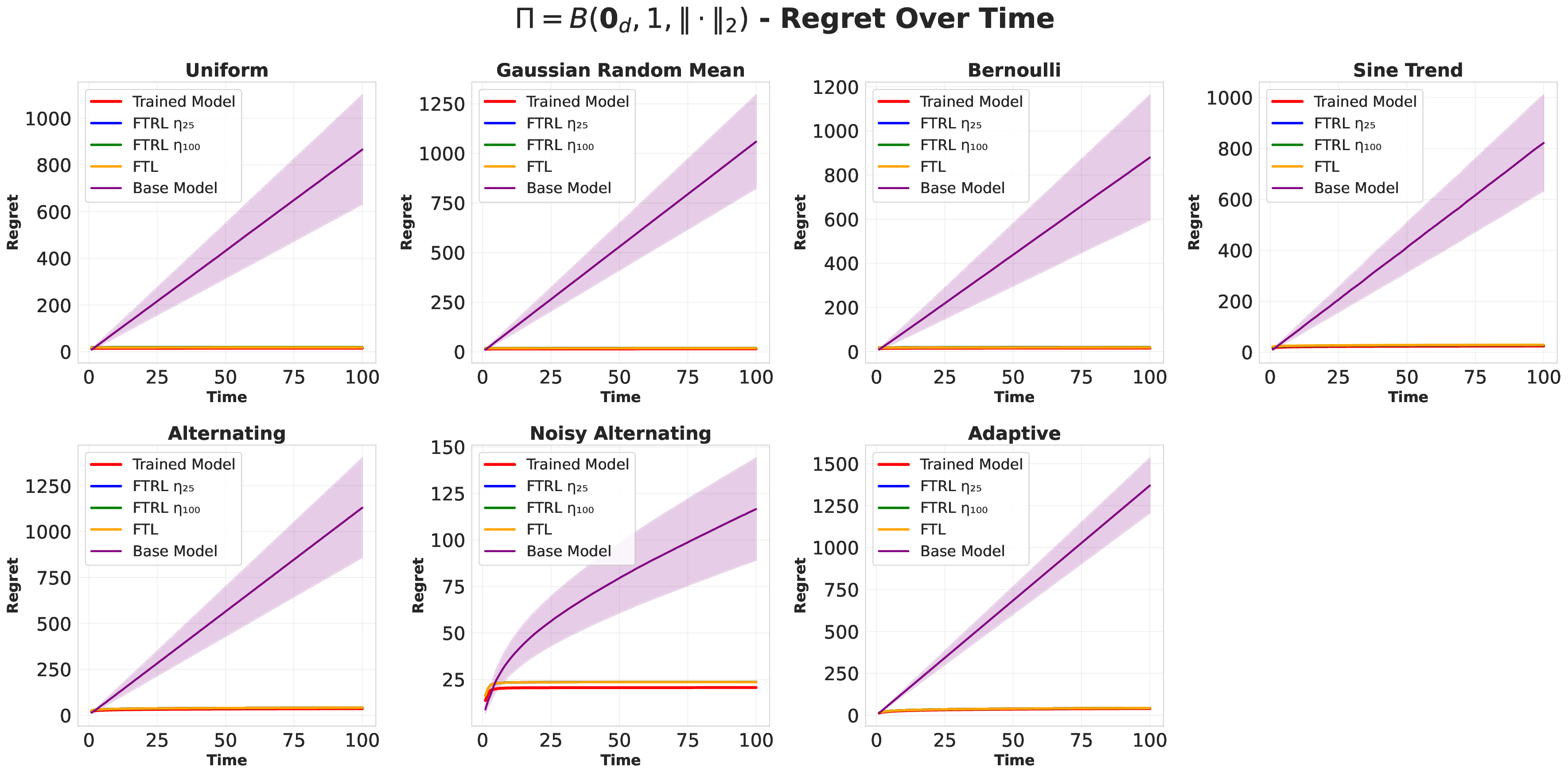
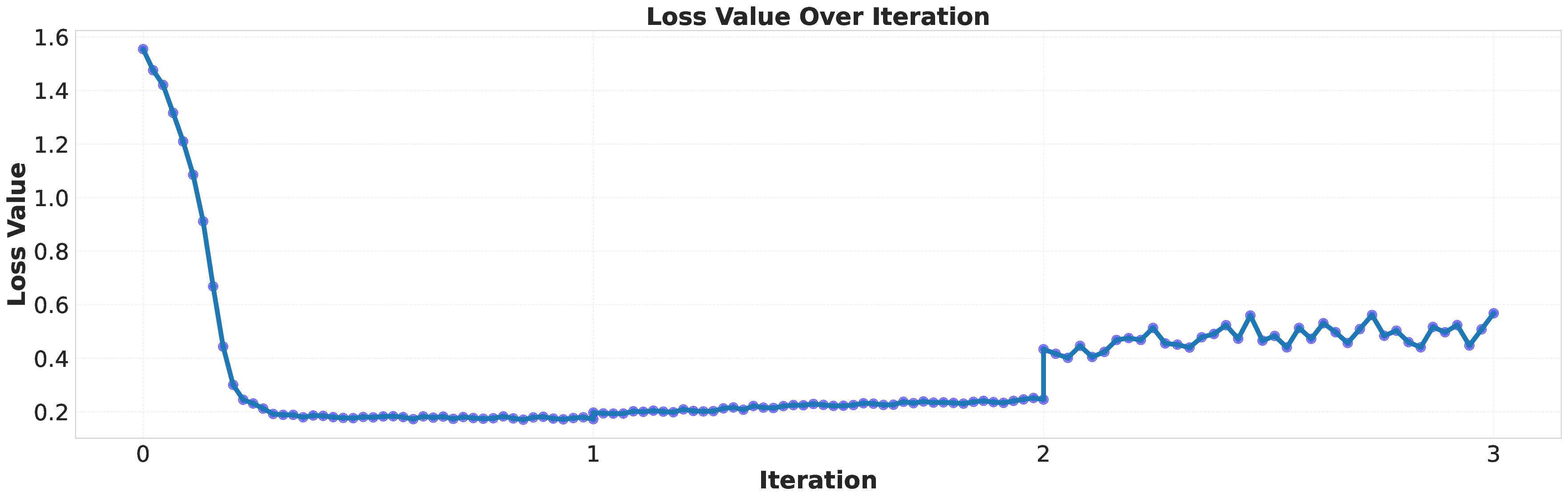
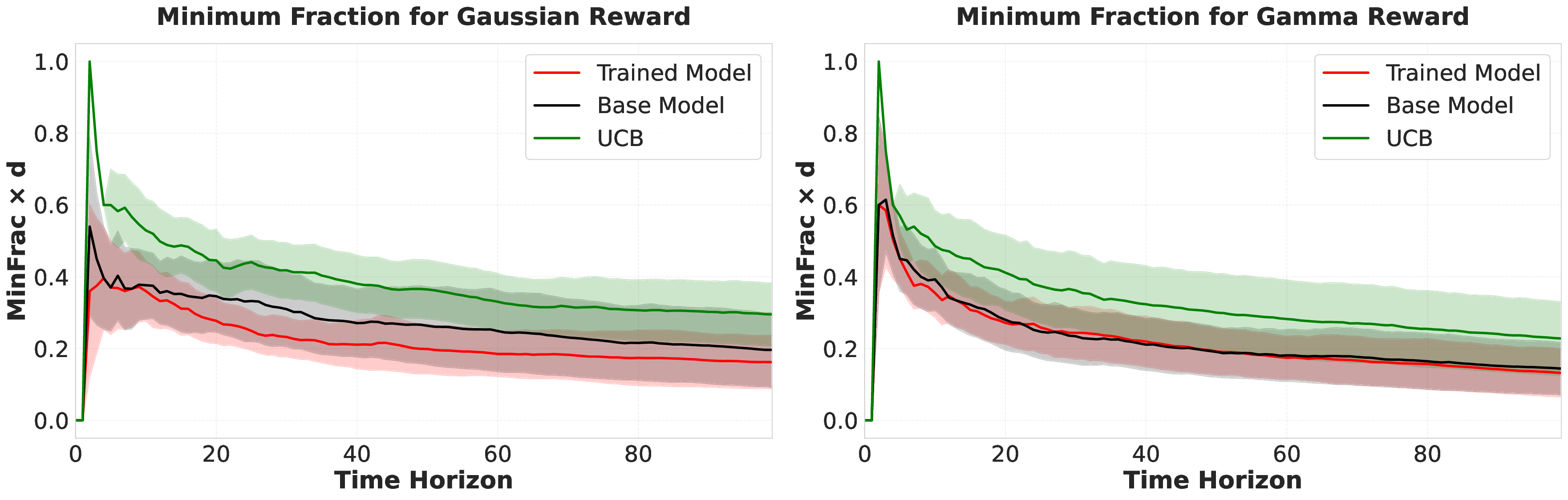
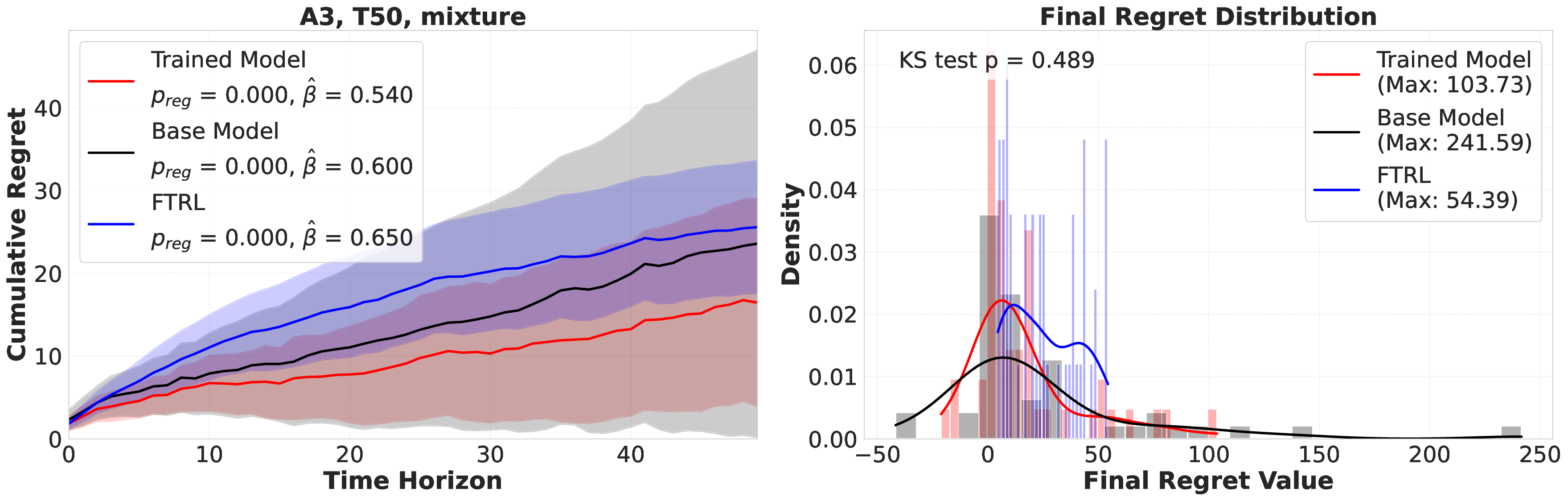
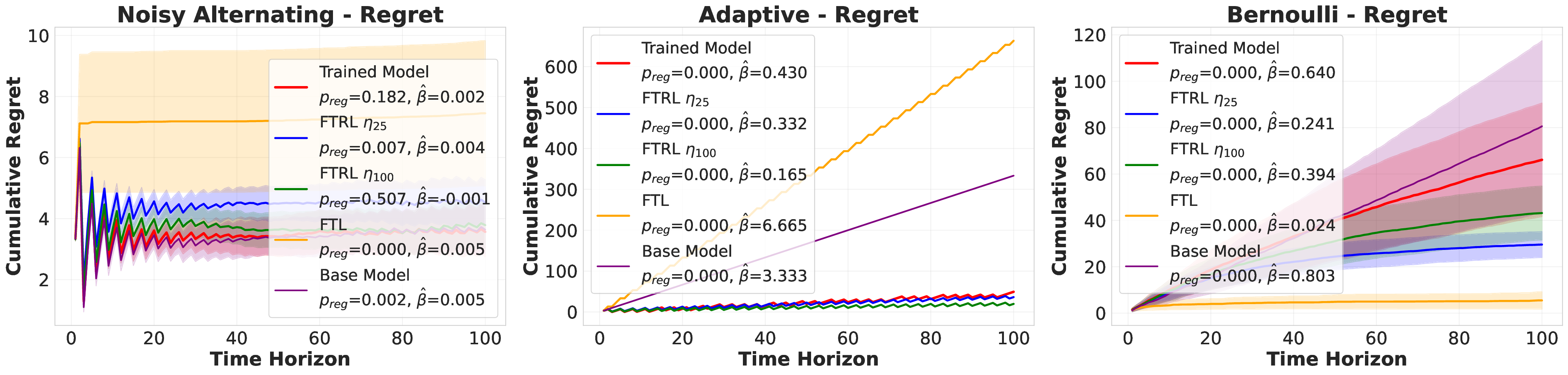
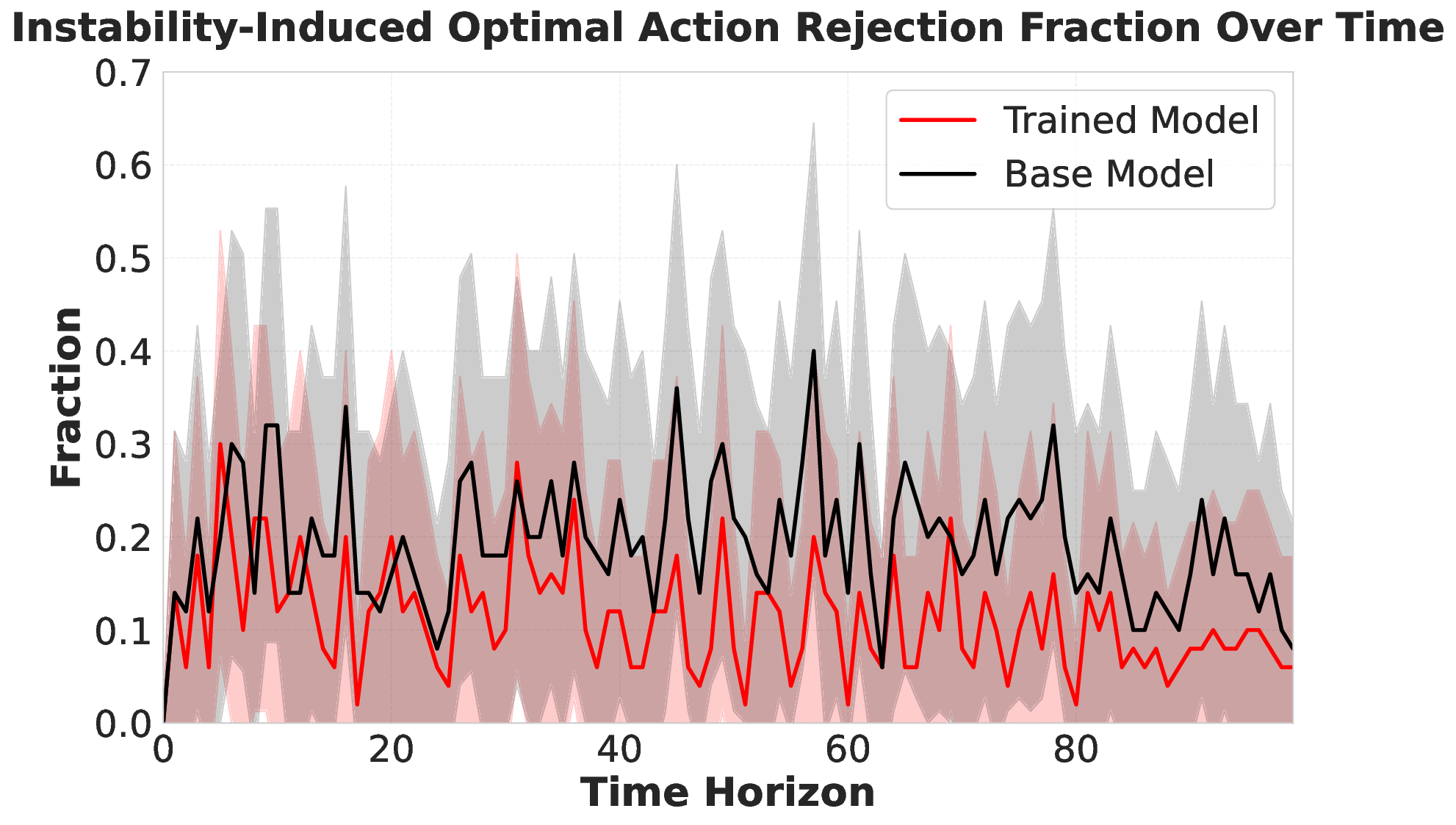
Large language models (LLMs) are increasingly deployed as "agents" for decision-making (DM) in interactive and dynamic environments. Yet, since they were not originally designed for DM, recent studies show that LLMs can struggle even in basic online DM problems, failing to achieve low regret or an effective exploration-exploitation tradeoff. To address this, we introduce Iterative Regret-Minimization Fine-Tuning (Iterative RMFT), a post-training procedure that repeatedly distills low-regret decision trajectories back into the base model. At each iteration, the model rolls out multiple decision trajectories, selects the k-lowest regret ones, and fine-tunes itself on them. Unlike prior methods that (a) distill action sequences from known DM algorithms or (b) rely on manually crafted chain-of-thought templates, our approach leverages the regret metric to elicit the model's own DM ability and reasoning rationales. This reliance on model-generated reasoning avoids rigid output engineering and provides more flexible, natural-language training signals. Empirical results show that Iterative RMFT improves LLMs' DM performance across diverse models - from Transformers with numerical input/output, to open-weight LLMs, and advanced closed-weight models like GPT-4o mini. Its flexibility in output and reasoning formats enables generalization across tasks with varying horizons, action spaces, reward processes, and natural-language contexts. Finally, we provide theoretical insight showing that a single-layer Transformer under this paradigm can act as a no-regret learner in a simplified setting. Overall, Iterative RMFT offers a principled and general post-training framework for enhancing LLMs' decision-making capabilities.

💡 Deep Analysis

📄 Full Content

📸 Image Gallery

Reference