A Proof of Learning Rate Transfer under $μ$P

📝 Original Info

• Title: A Proof of Learning Rate Transfer under $μ$P
• ArXiv ID: 2511.01734
• Date: 2025-11-03
• Authors: 정보 없음 (논문에 저자 정보가 제공되지 않았습니다.)

📝 Abstract

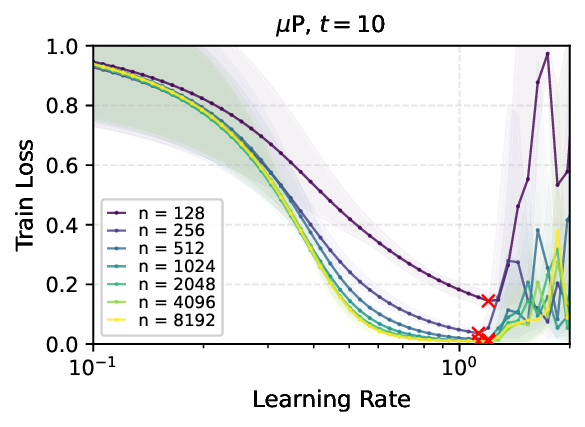
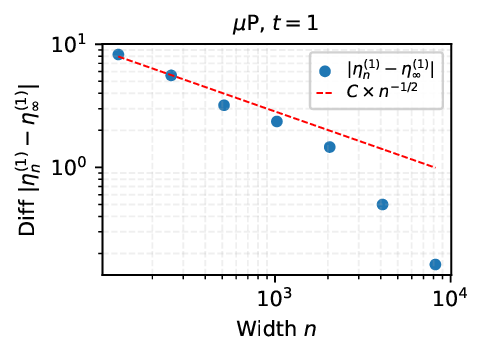
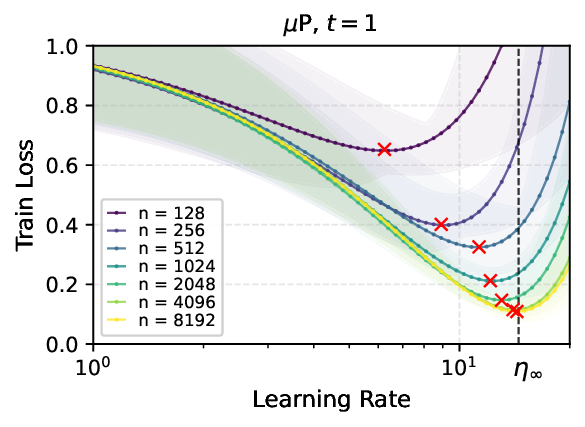
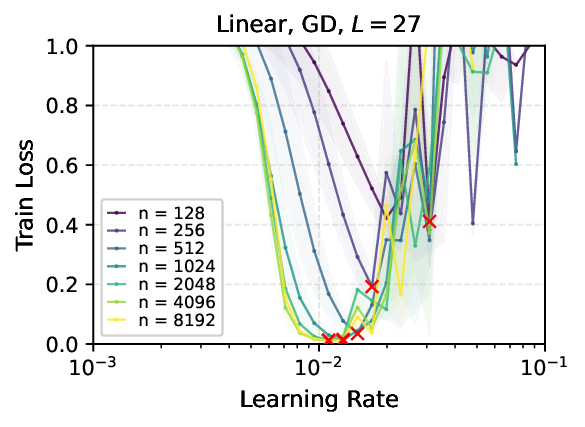
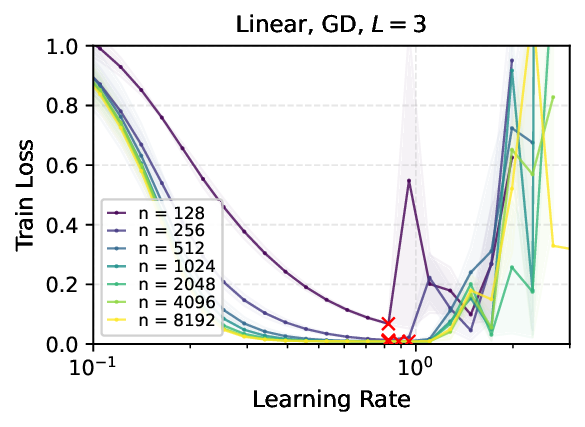
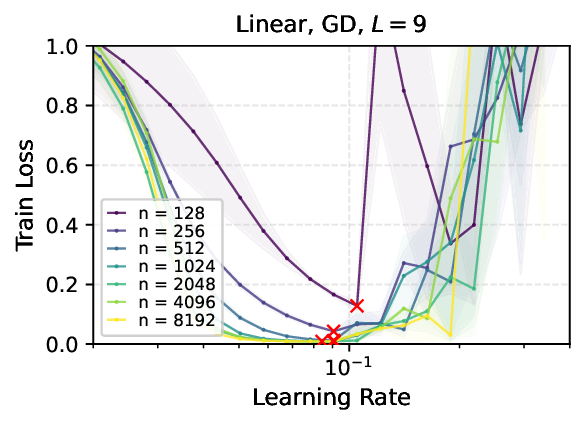
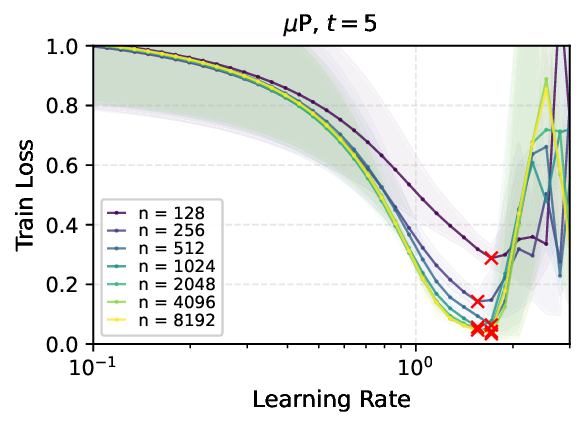
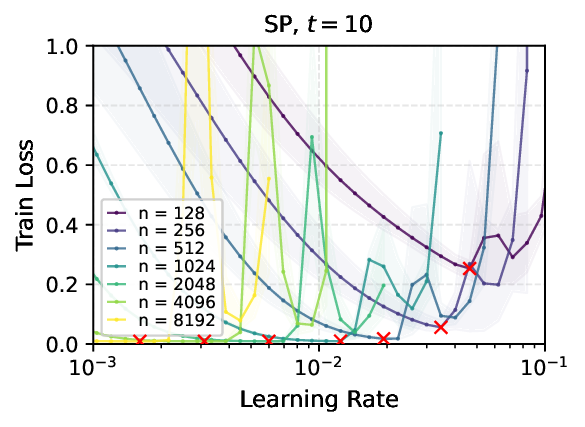
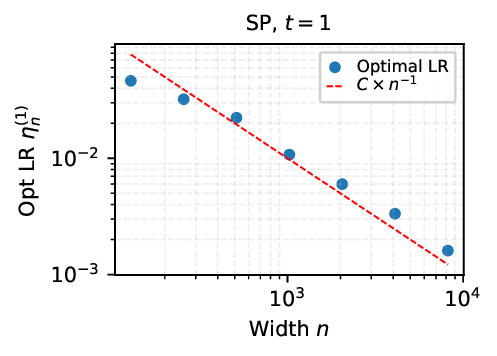
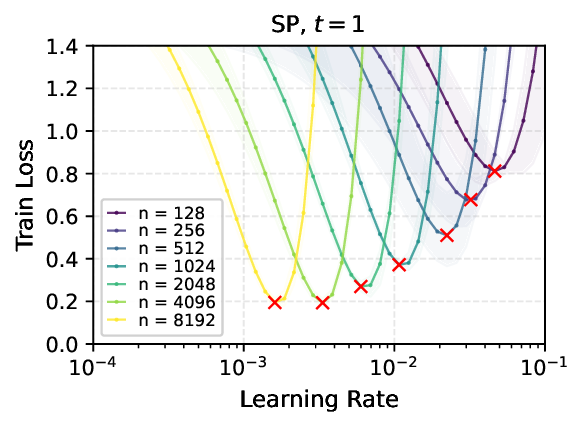
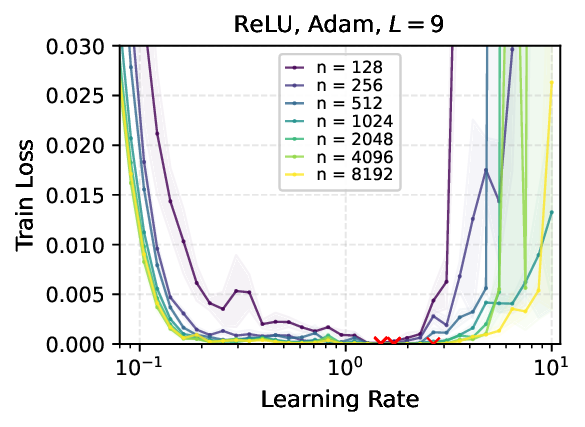
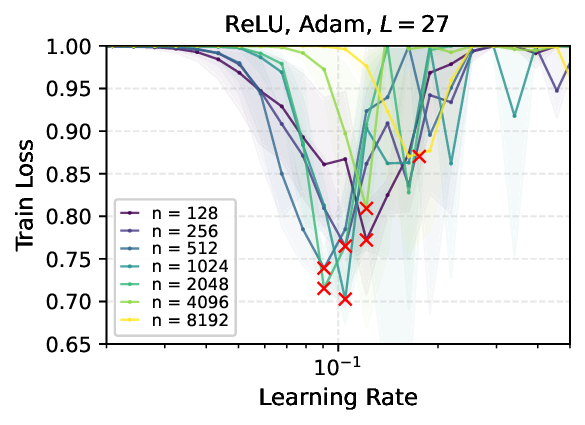
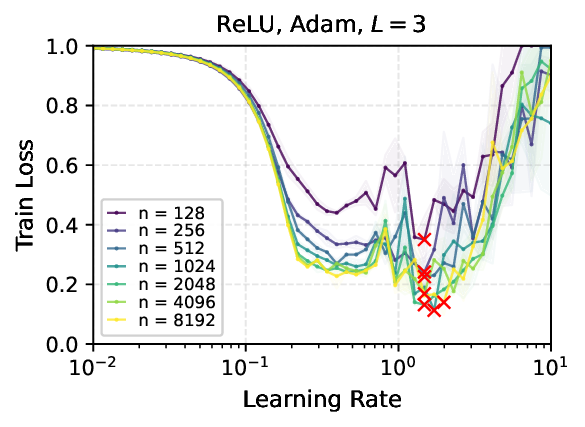
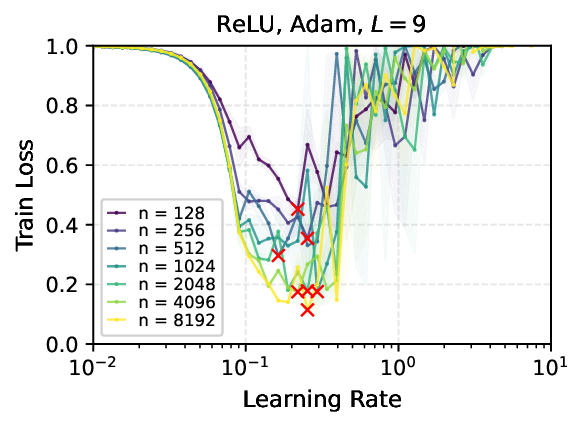
We provide the first proof of learning rate transfer with width in a linear multi-layer perceptron (MLP) parametrized with $μ$P, a neural network parameterization designed to ``maximize'' feature learning in the infinite-width limit. We show that under $μP$, the optimal learning rate converges to a \emph{non-zero constant} as width goes to infinity, providing a theoretical explanation to learning rate transfer. In contrast, we show that this property fails to hold under alternative parametrizations such as Standard Parametrization (SP) and Neural Tangent Parametrization (NTP). We provide intuitive proofs and support the theoretical findings with extensive empirical results.

💡 Deep Analysis

📄 Full Content

📸 Image Gallery

Reference