DeepContour: A Hybrid Deep Learning Framework for Accelerating Generalized Eigenvalue Problem Solving via Efficient Contour Design

📝 Original Info

• Title: DeepContour: A Hybrid Deep Learning Framework for Accelerating Generalized Eigenvalue Problem Solving via Efficient Contour Design
• ArXiv ID: 2511.01927
• Date: 2025-11-02
• Authors: ** 정보 없음 (논문에 저자 정보가 제공되지 않음) **

📝 Abstract

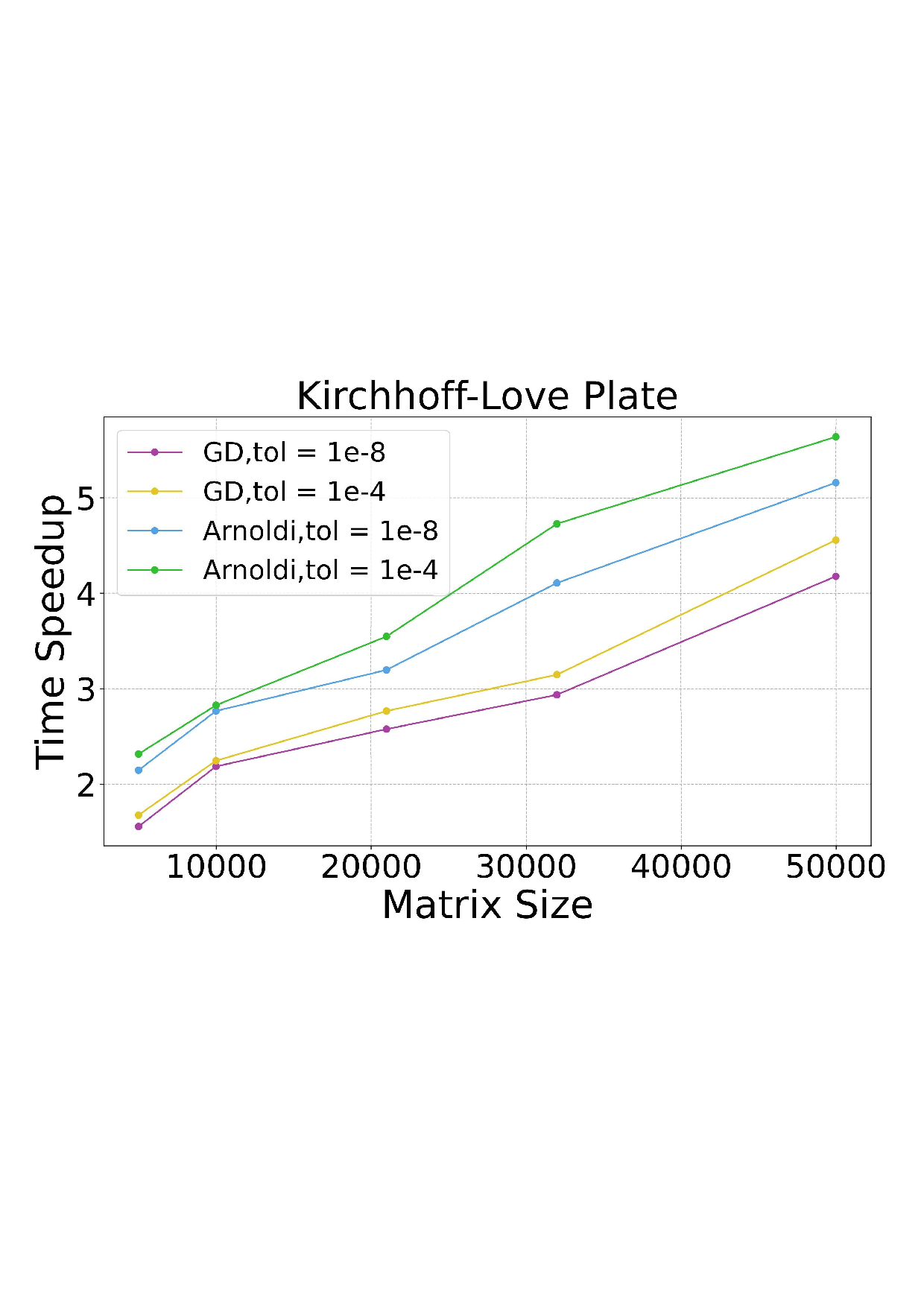
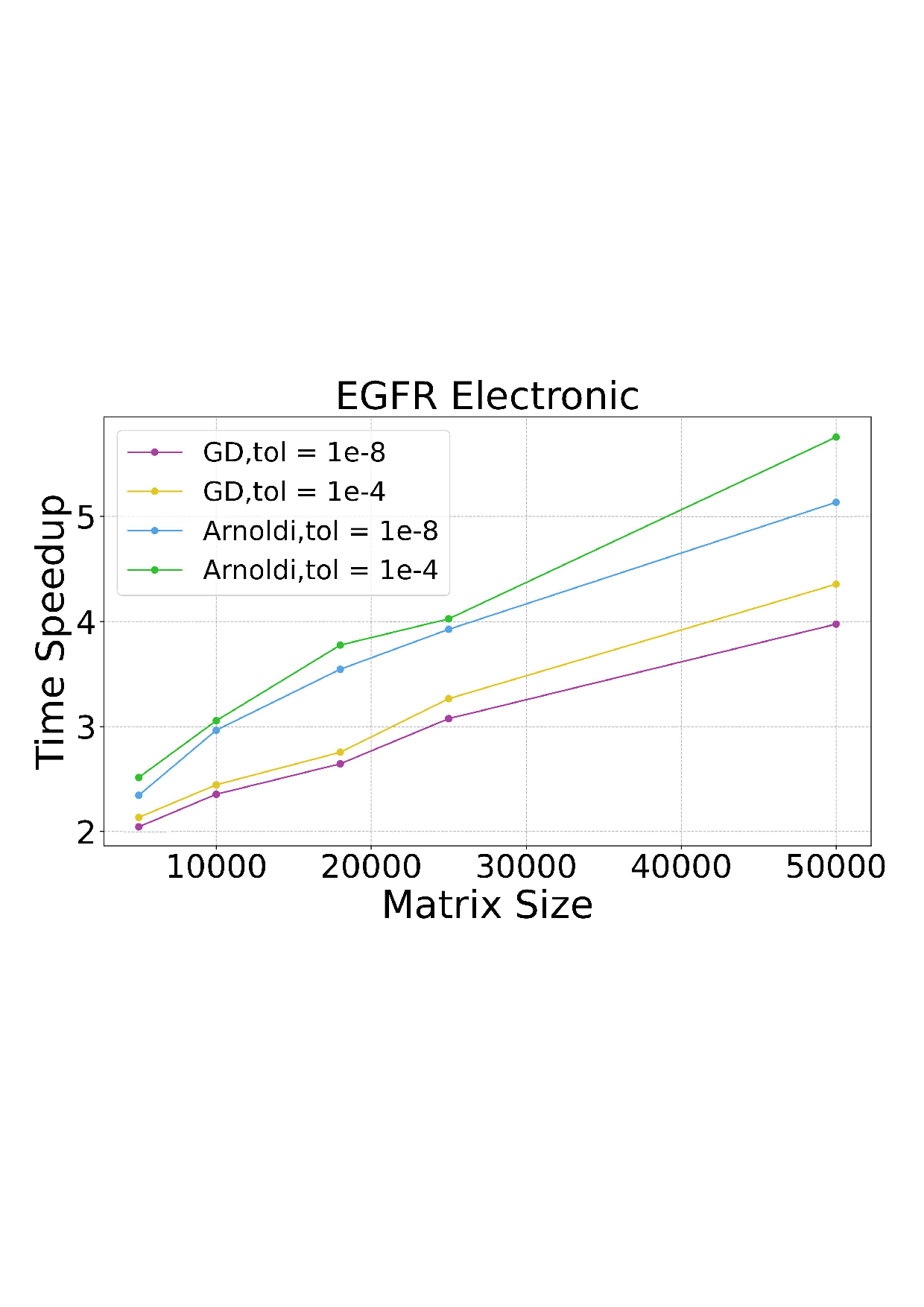
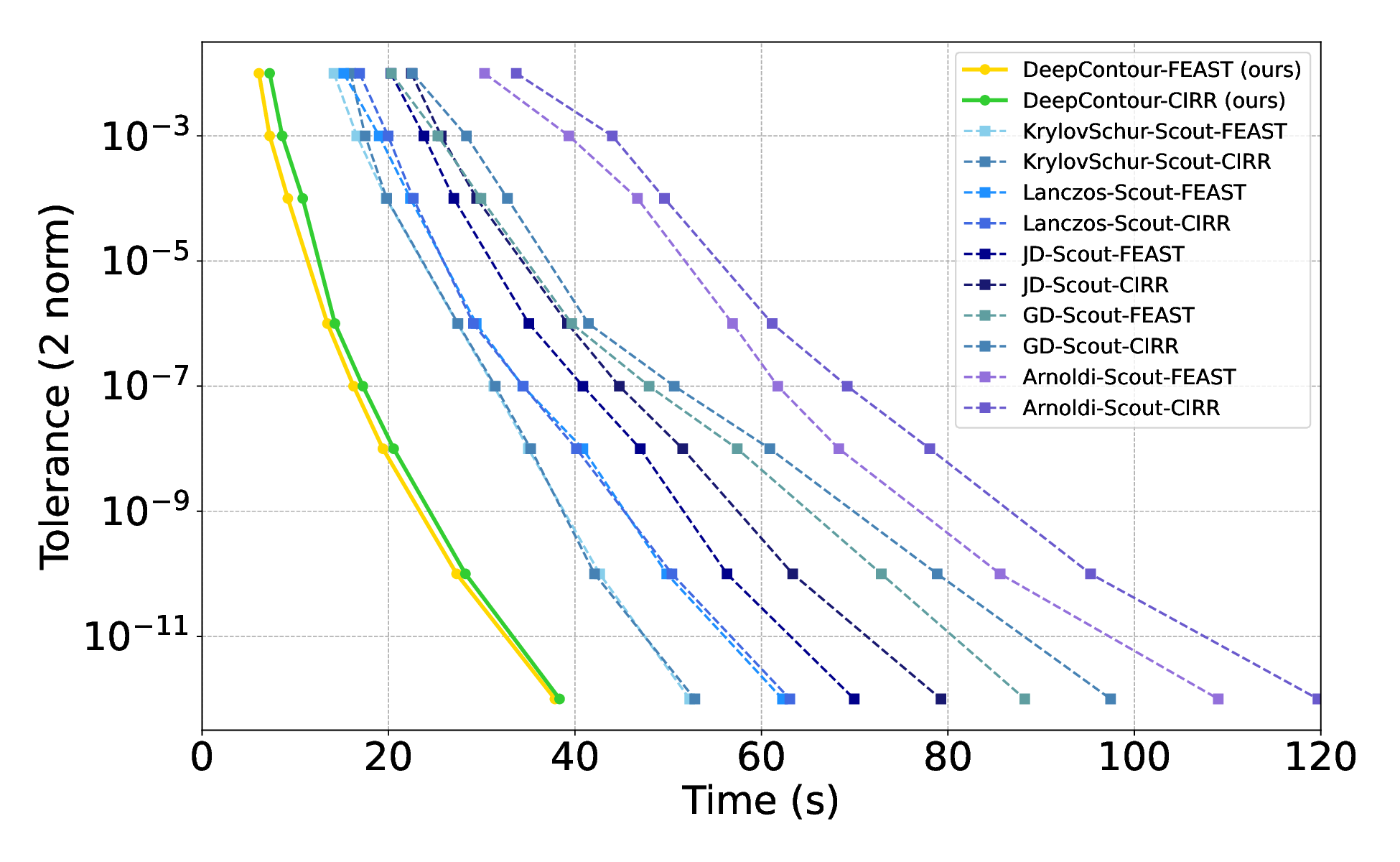
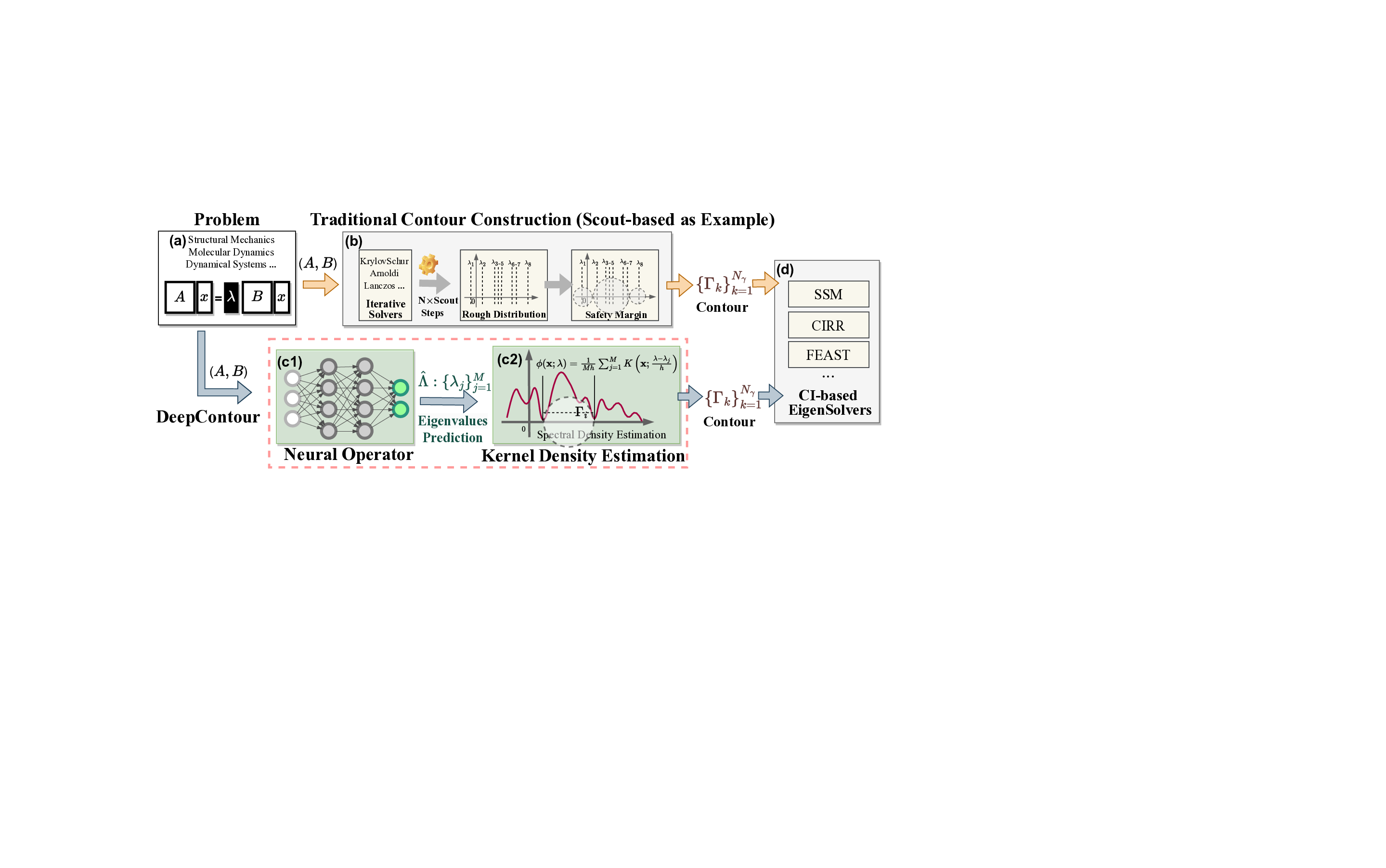
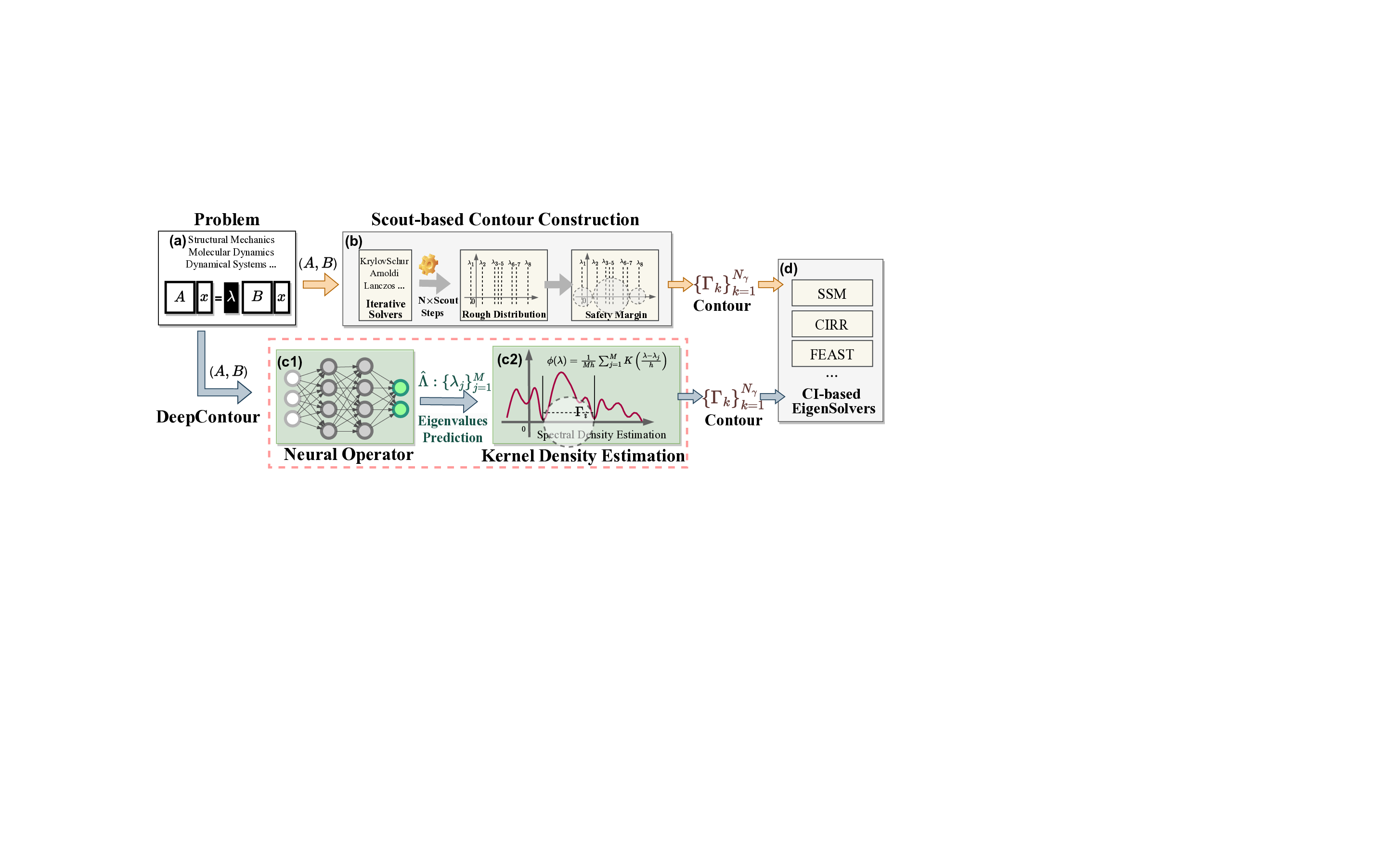
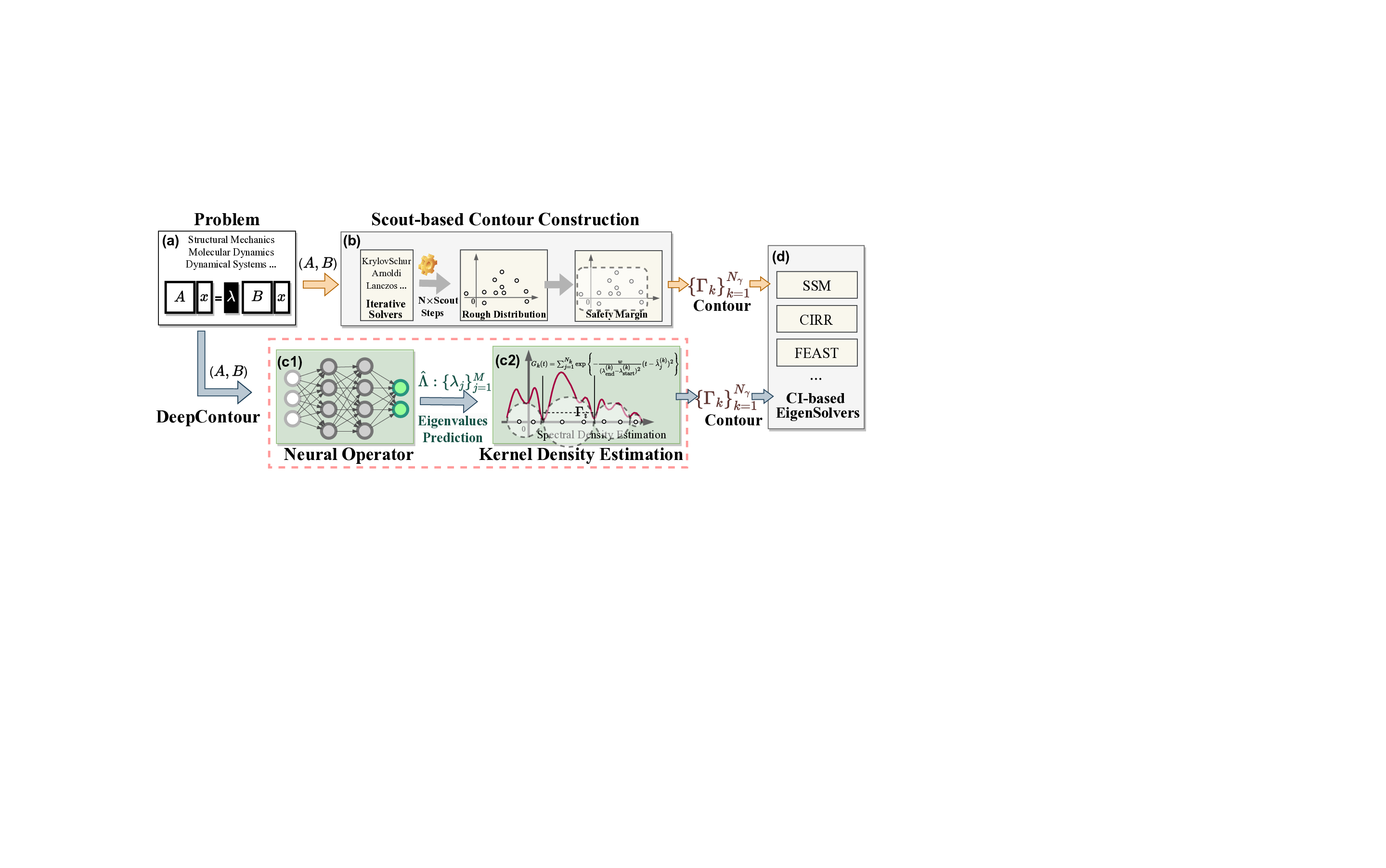
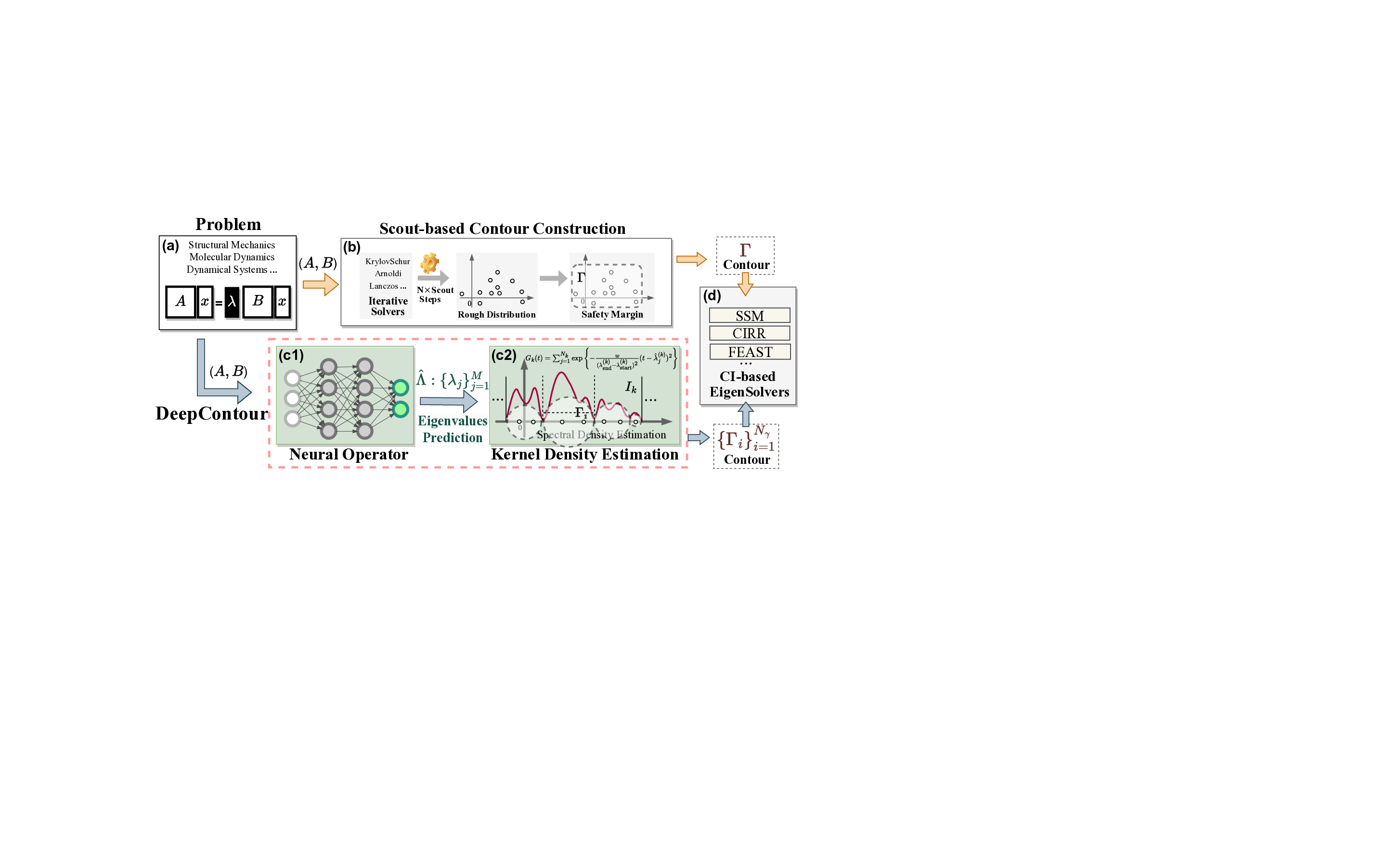
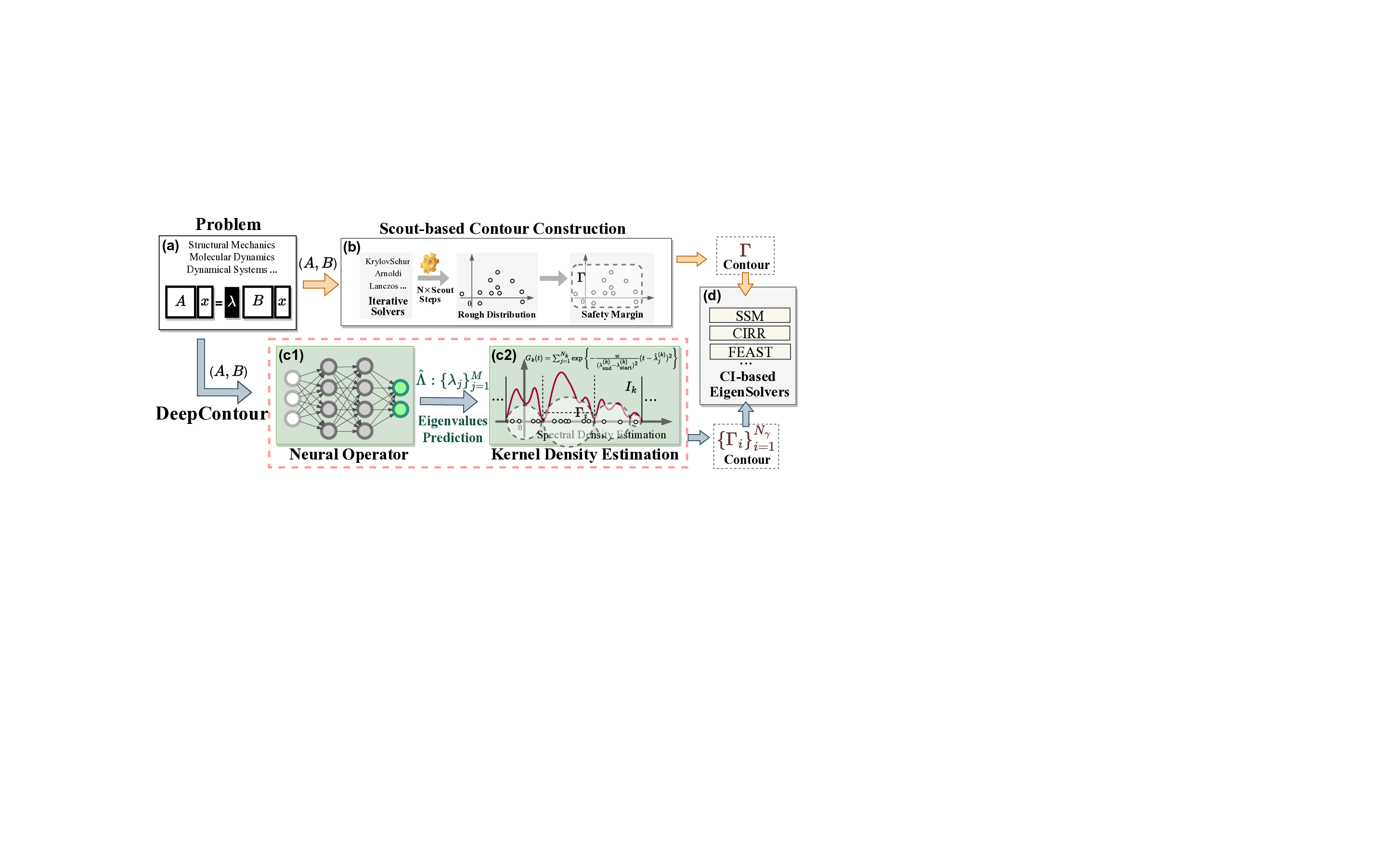
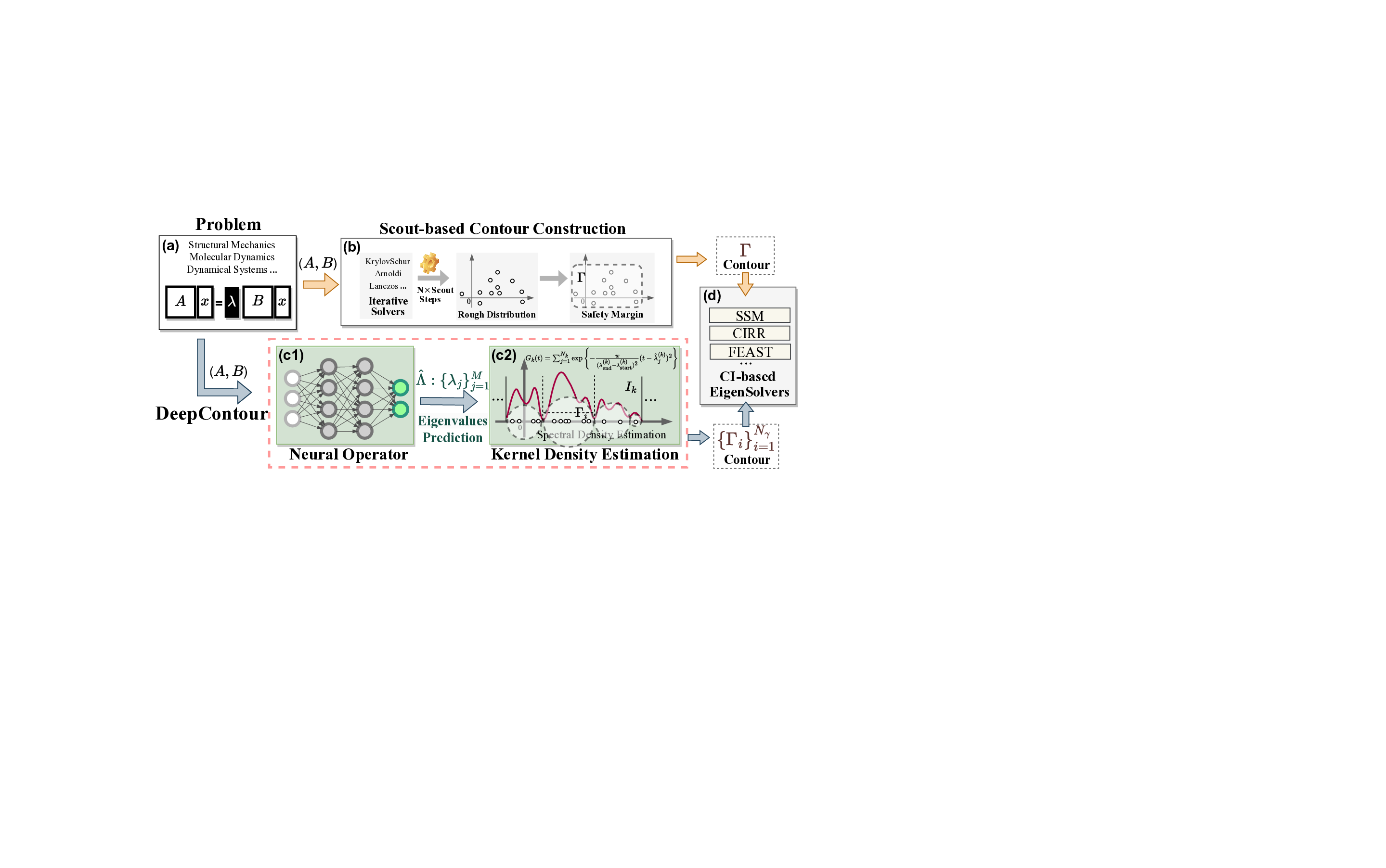
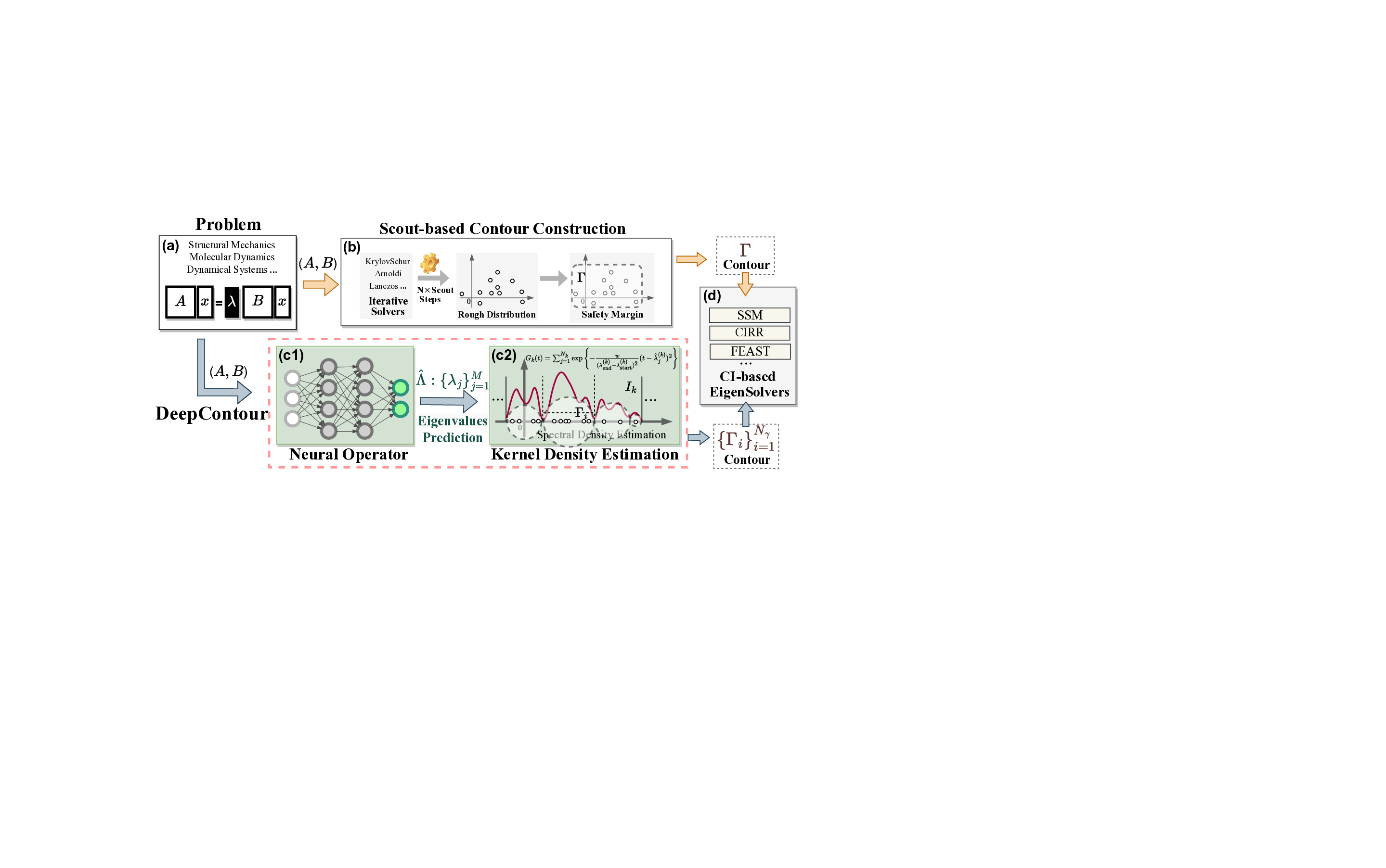
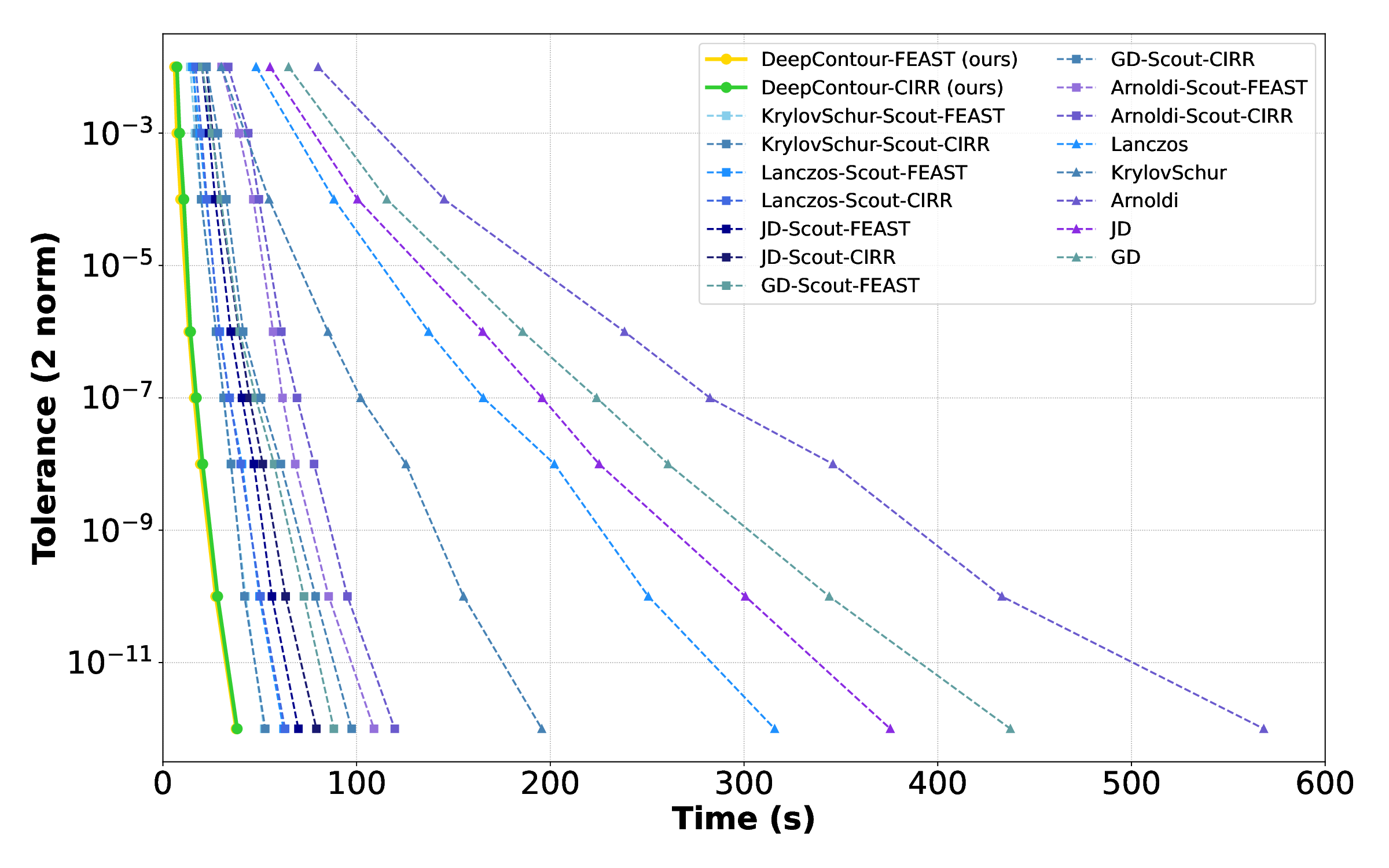
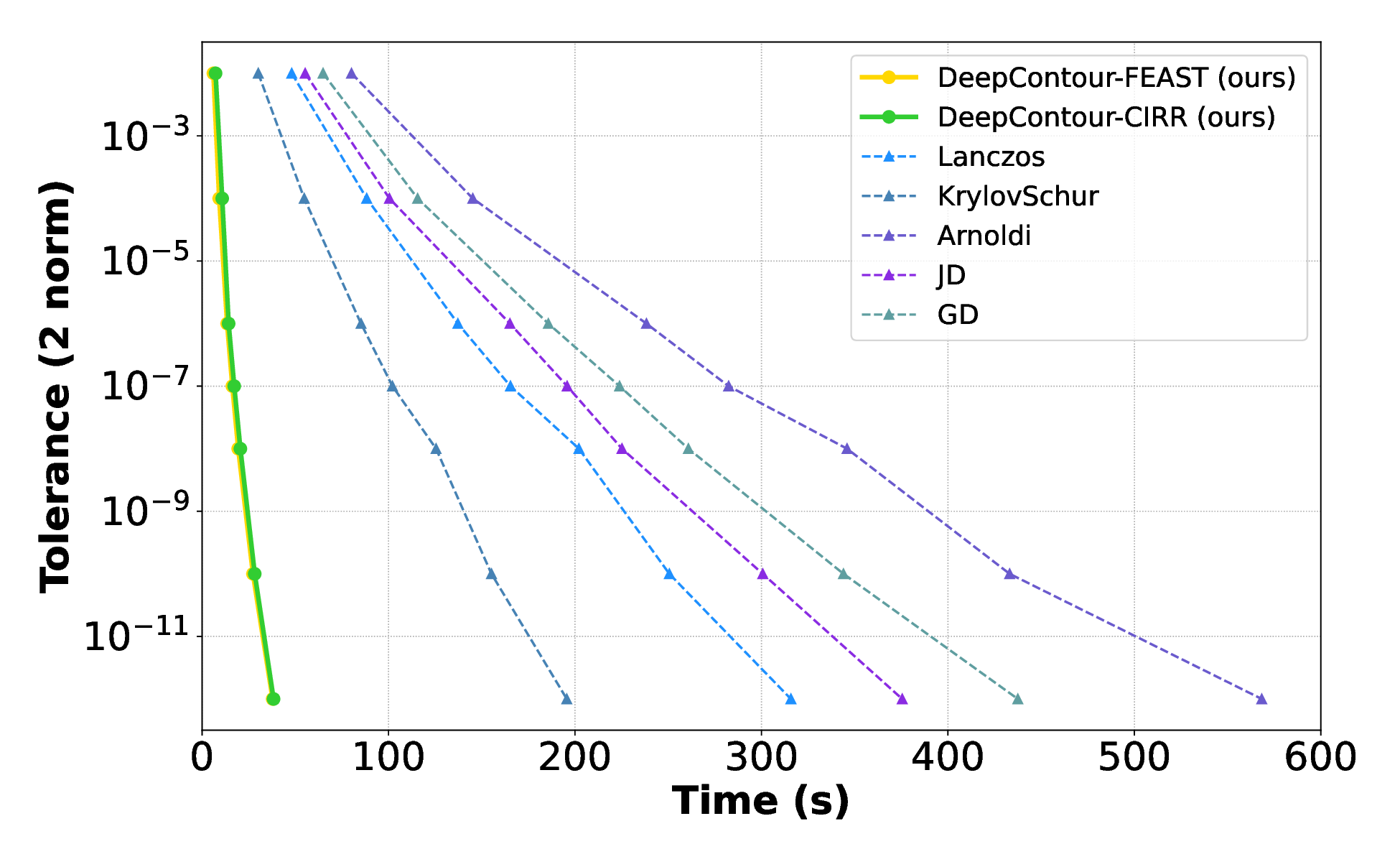
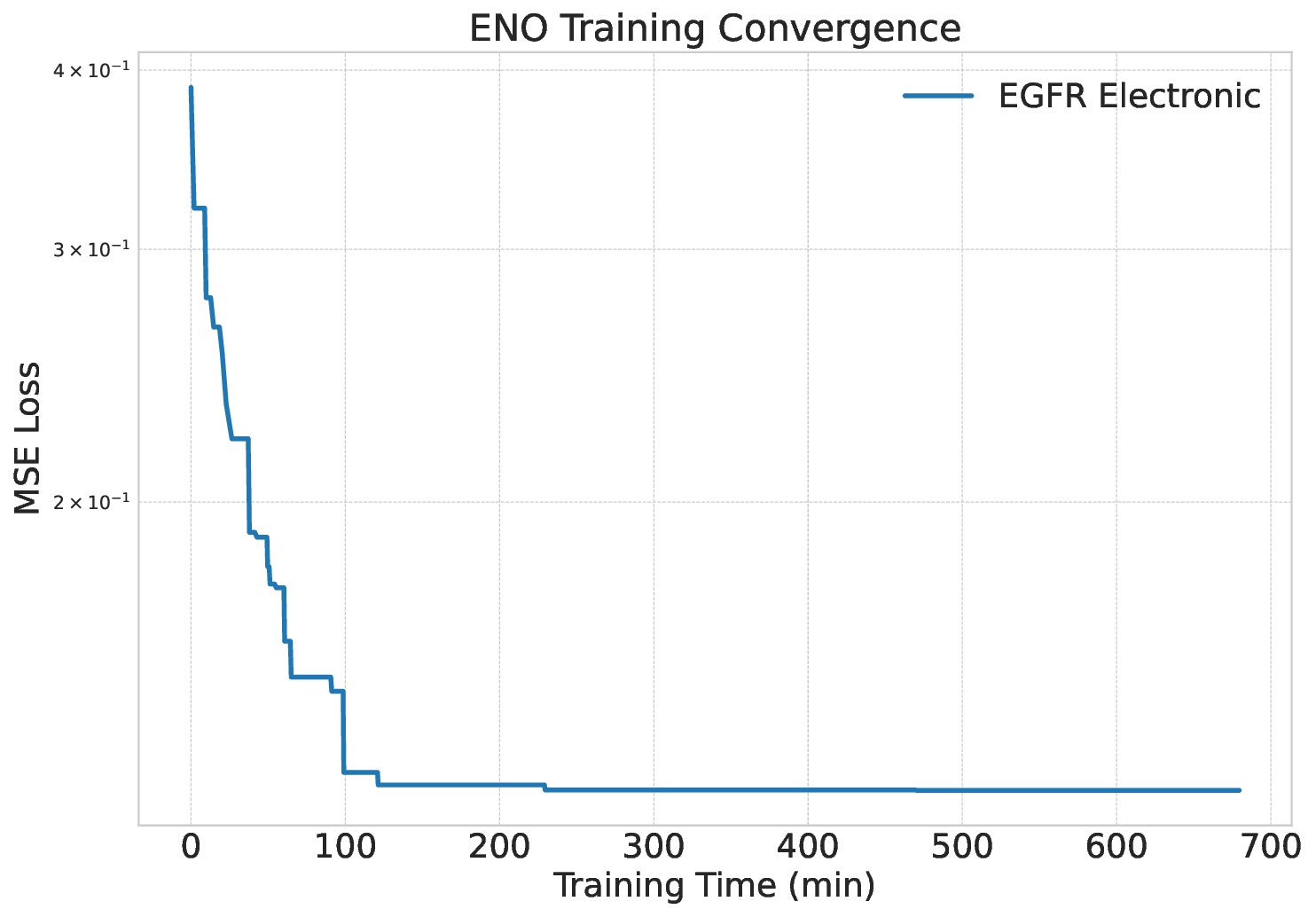
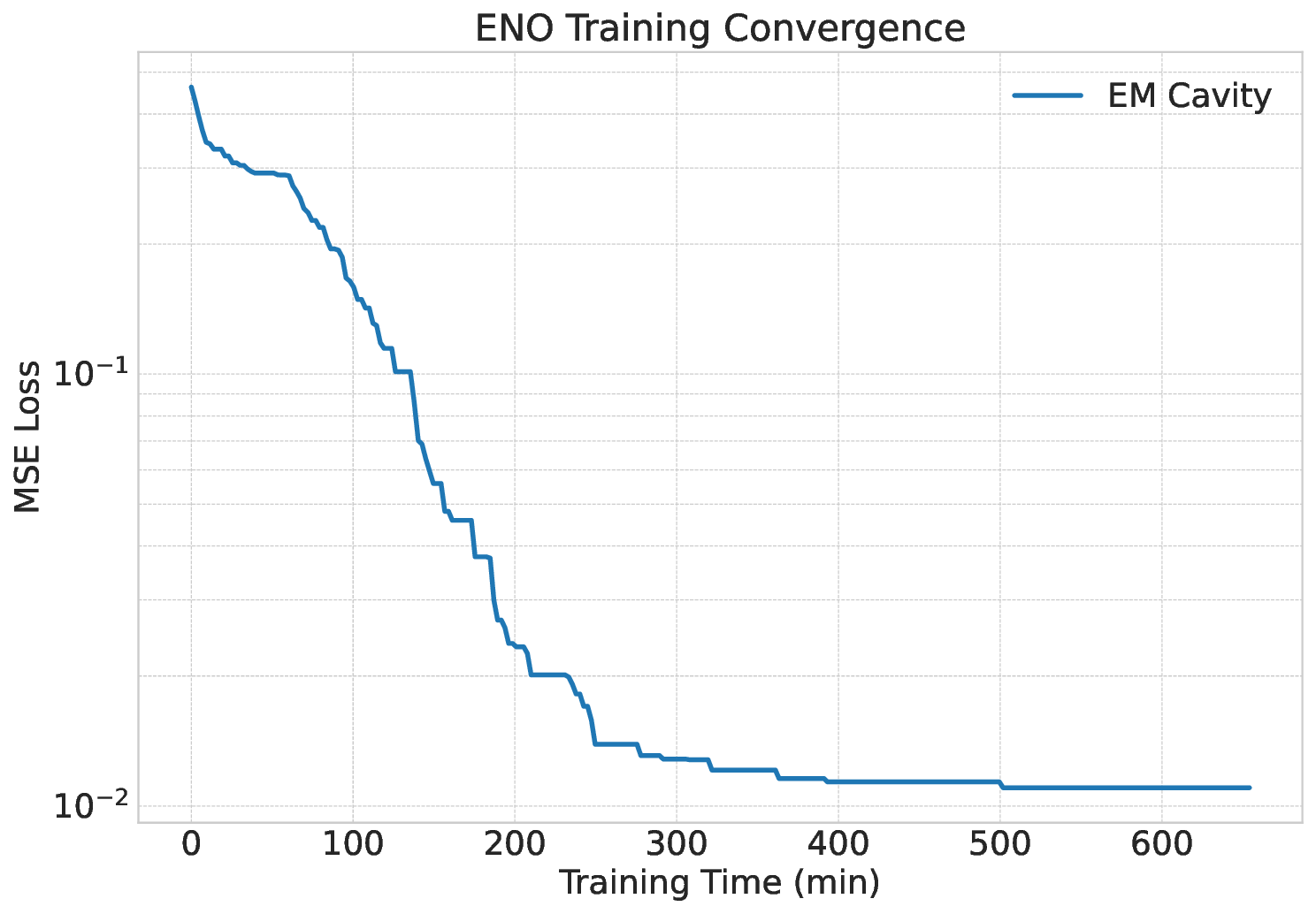
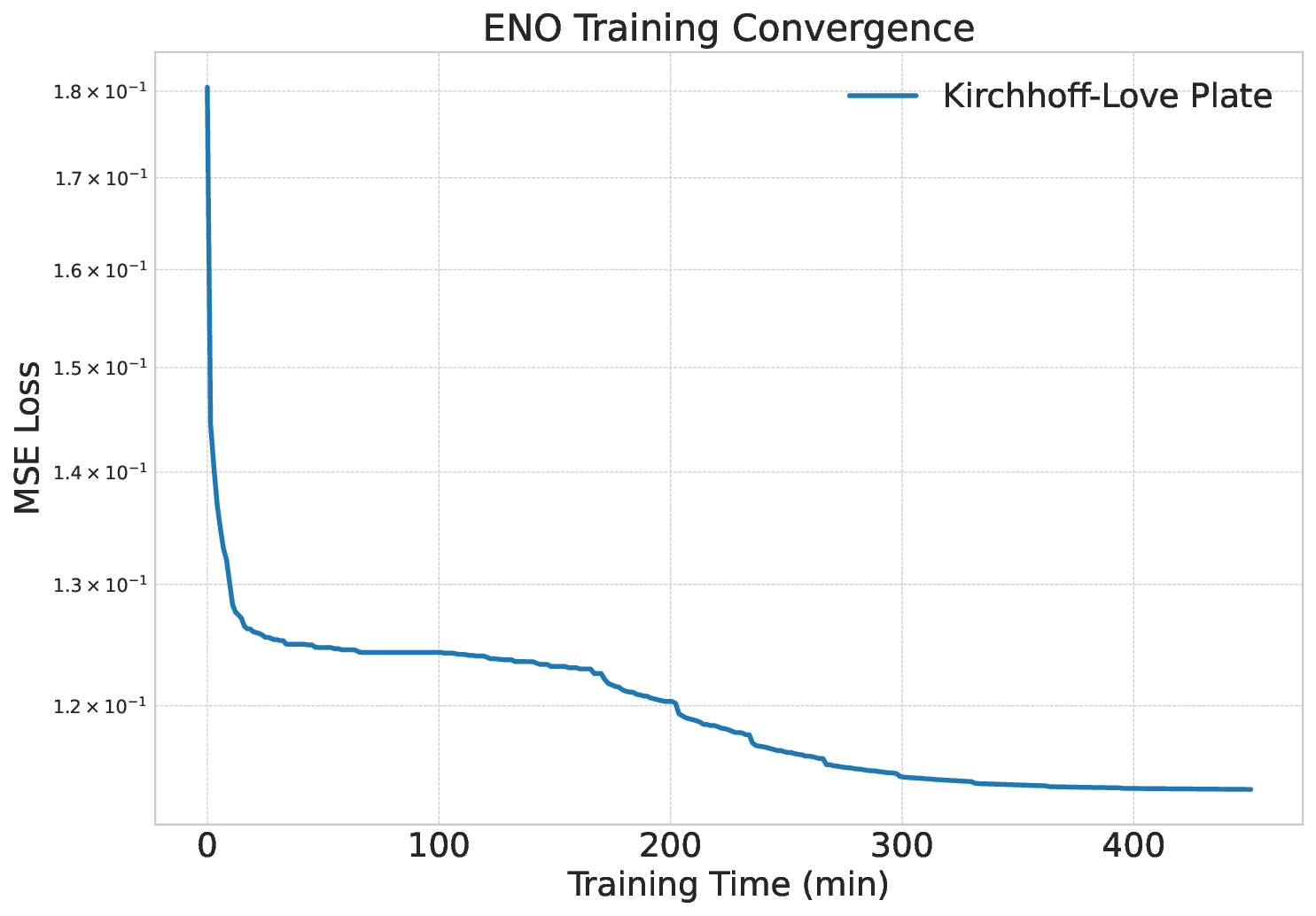
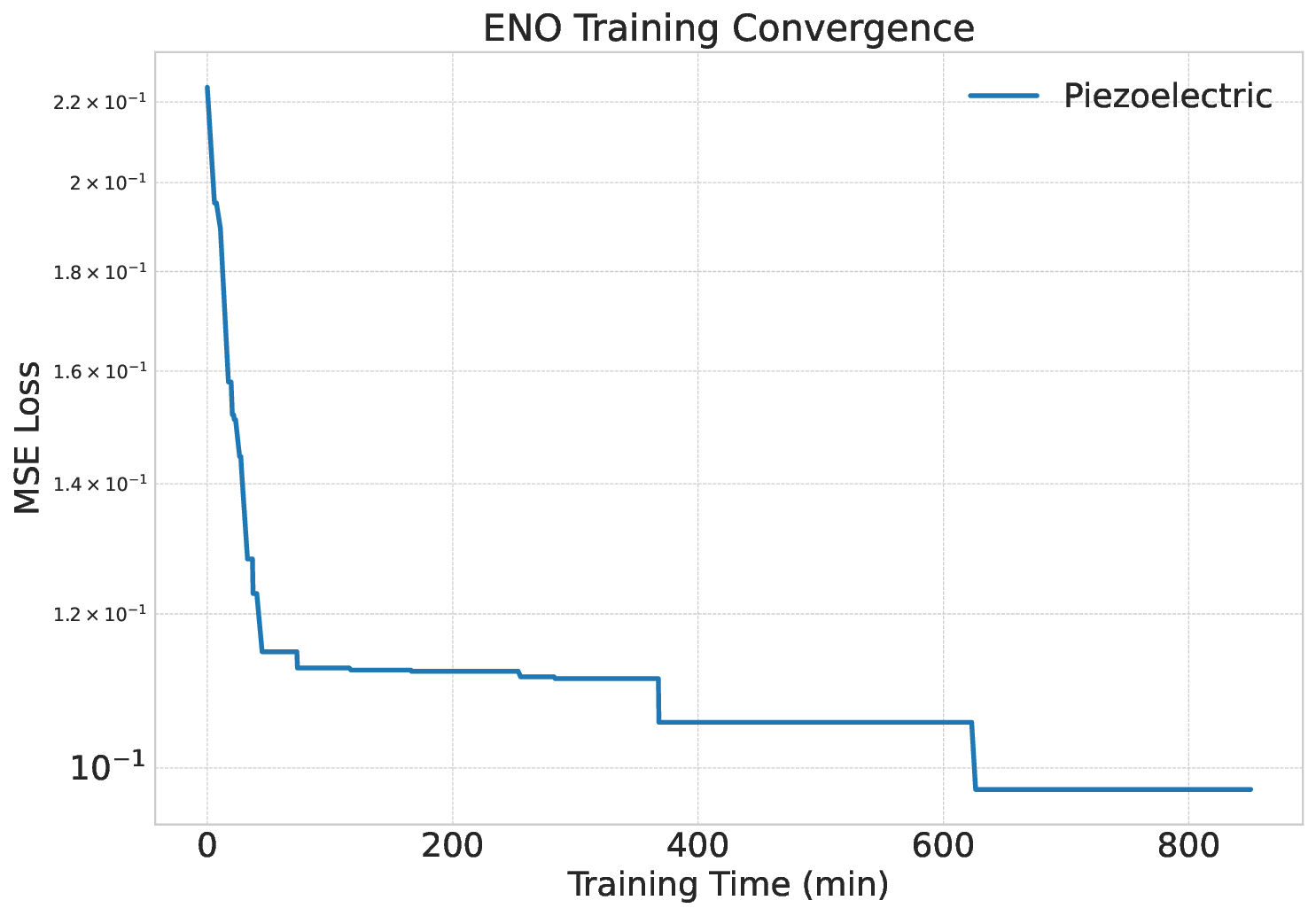
Solving large-scale Generalized Eigenvalue Problems (GEPs) is a fundamental yet computationally prohibitive task in science and engineering. As a promising direction, contour integral (CI) methods, such as the CIRR algorithm, offer an efficient and parallelizable framework. However, their performance is critically dependent on the selection of integration contours -- improper selection without reliable prior knowledge of eigenvalue distribution can incur significant computational overhead and compromise numerical accuracy. To address this challenge, we propose DeepContour, a novel hybrid framework that integrates a deep learning-based spectral predictor with Kernel Density Estimation for principled contour design. Specifically, DeepContour first employs a Fourier Neural Operator (FNO) to rapidly predict the spectral distribution of a given GEP. Subsequently, Kernel Density Estimation (KDE) is applied to the predicted spectrum to automatically and systematically determine proper integration contours. Finally, these optimized contours guide the CI solver to efficiently find the desired eigenvalues. We demonstrate the effectiveness of our method on diverse challenging scientific problems. In our main experiments, DeepContour accelerates GEP solving across multiple datasets, achieving up to a 5.63$\times$ speedup. By combining the predictive power of deep learning with the numerical rigor of classical solvers, this work pioneers an efficient and robust paradigm for tackling difficult generalized eigenvalue involving matrices of high dimension.

💡 Deep Analysis

📄 Full Content

📸 Image Gallery

Reference