Efficient Reinforcement Learning for Large Language Models with Intrinsic Exploration

📝 Original Info

• Title: Efficient Reinforcement Learning for Large Language Models with Intrinsic Exploration
• ArXiv ID: 2511.00794
• Date: 2025-11-02
• Authors: ** (논문에 명시된 저자 정보가 제공되지 않아 알 수 없습니다.) **

📝 Abstract

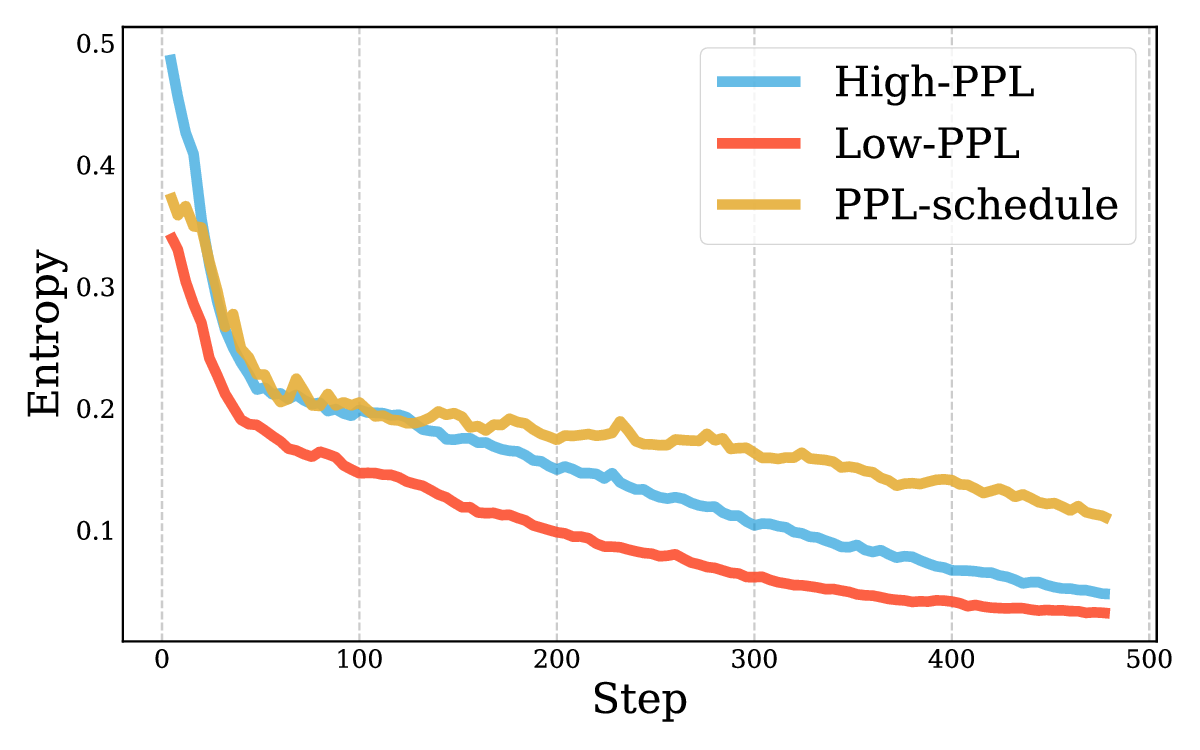
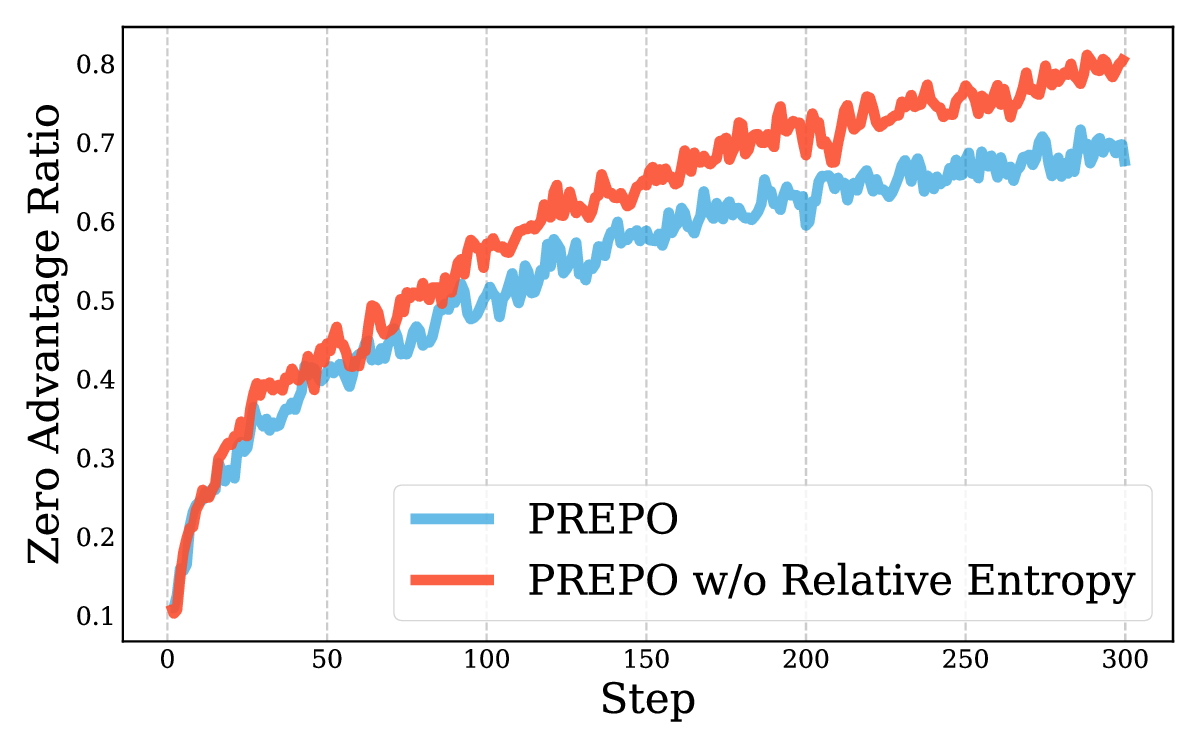
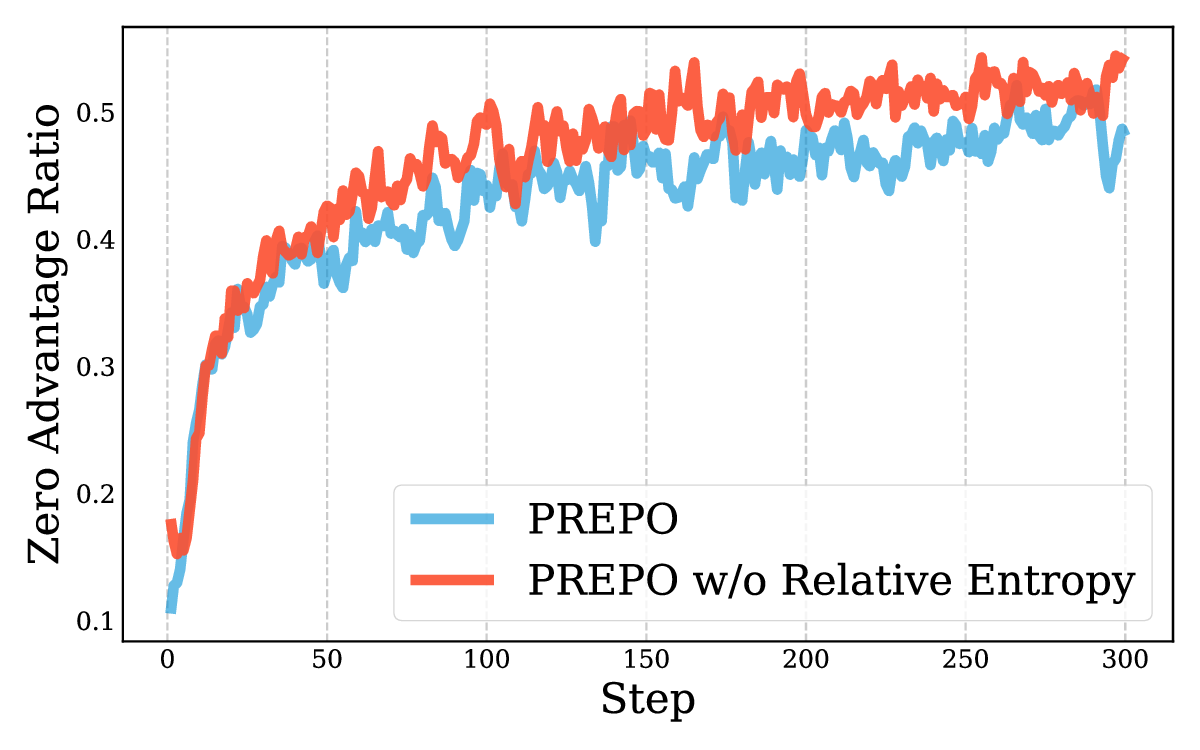
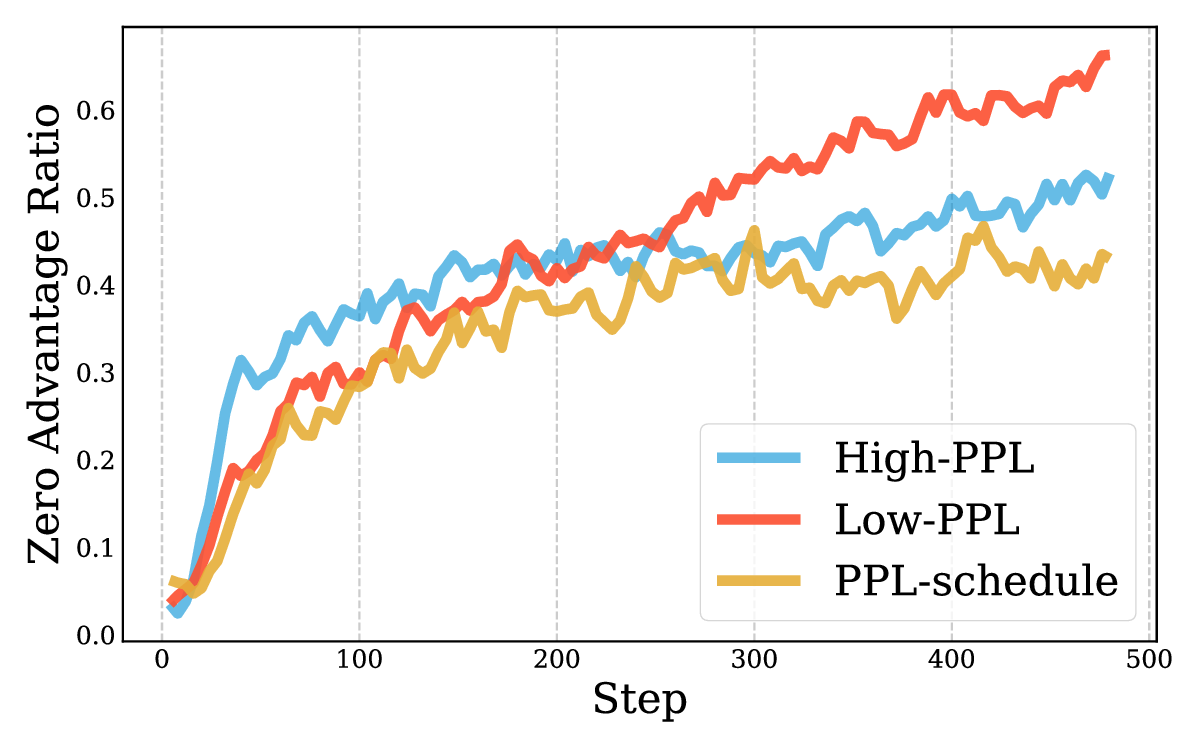
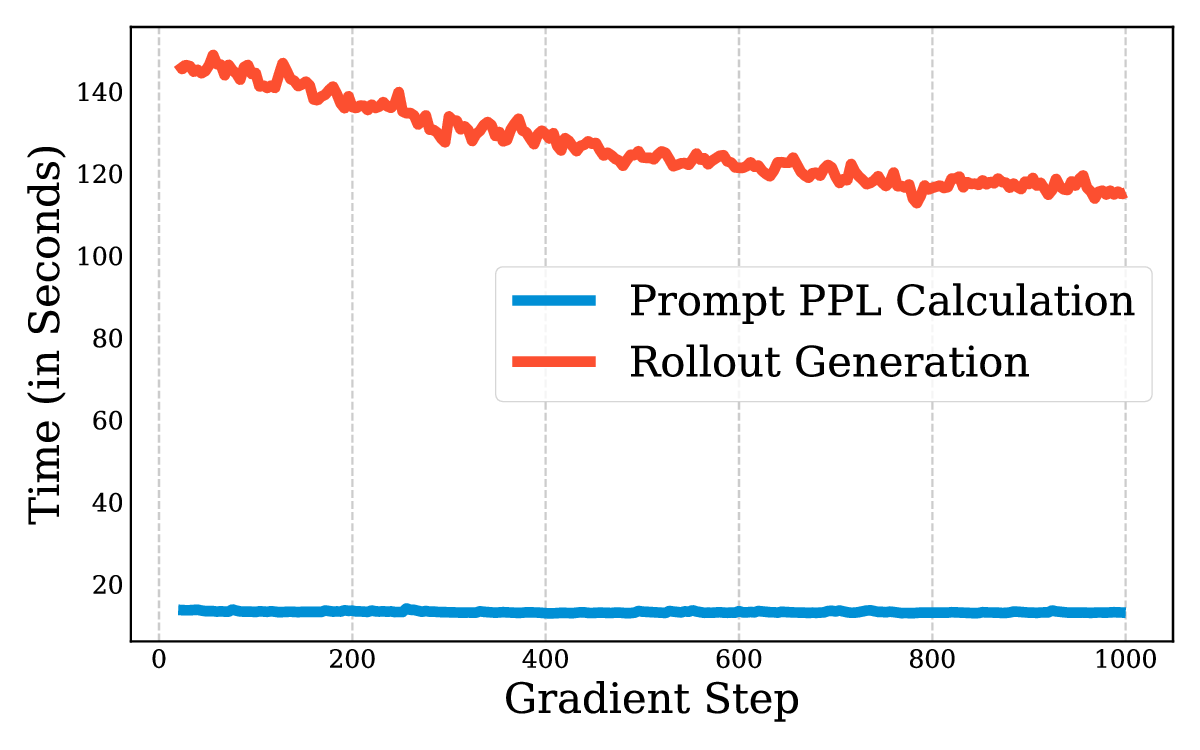
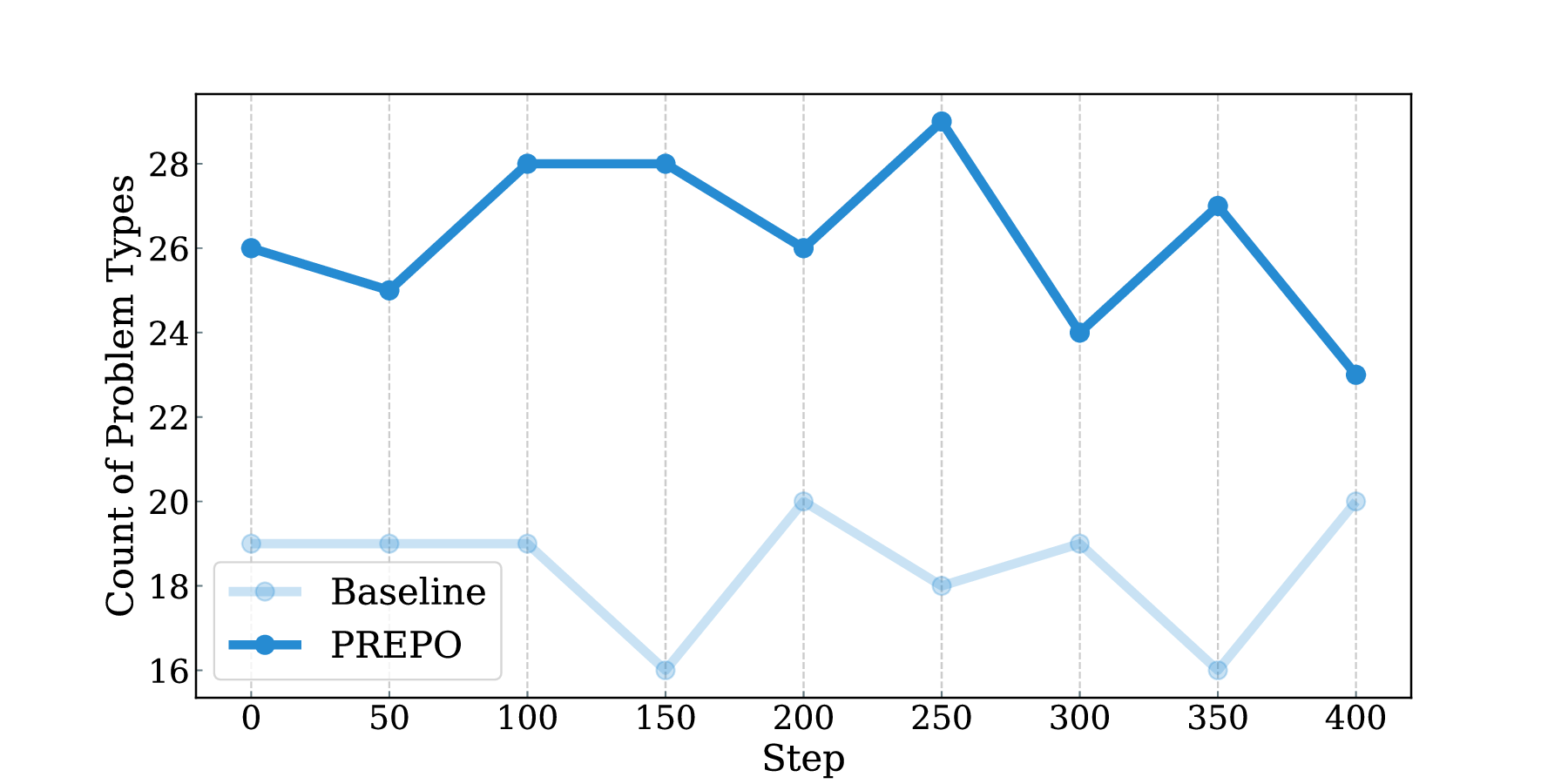
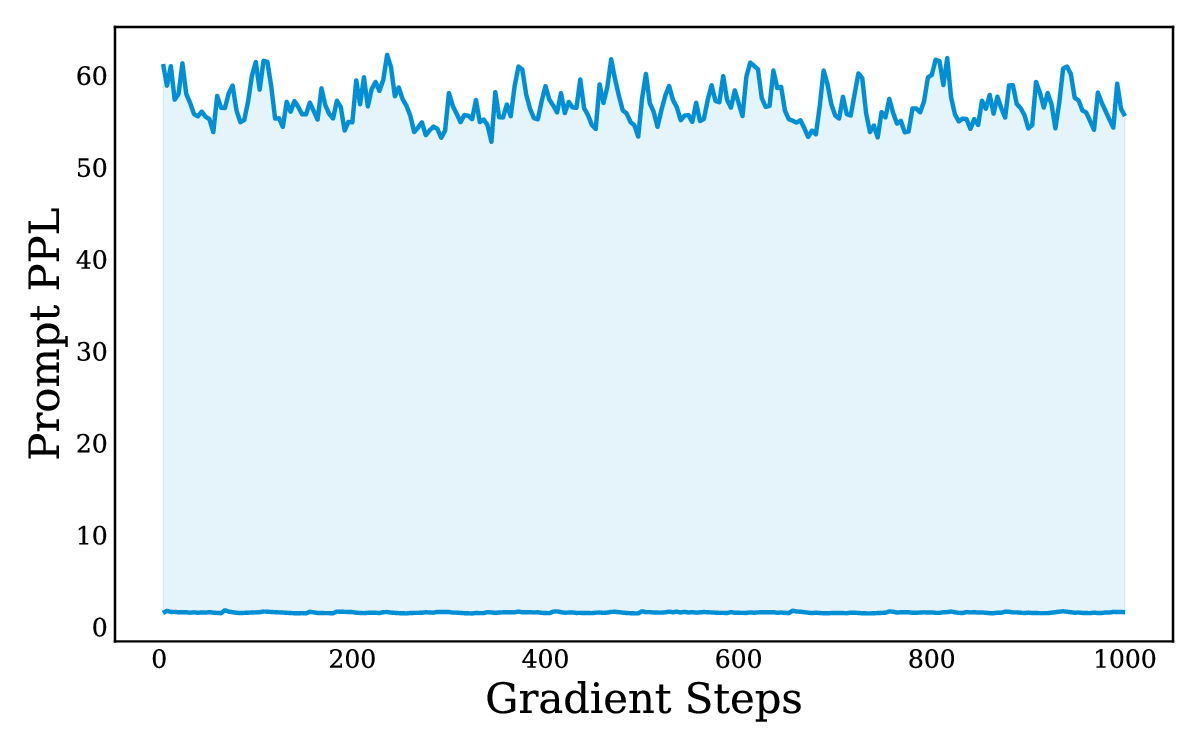
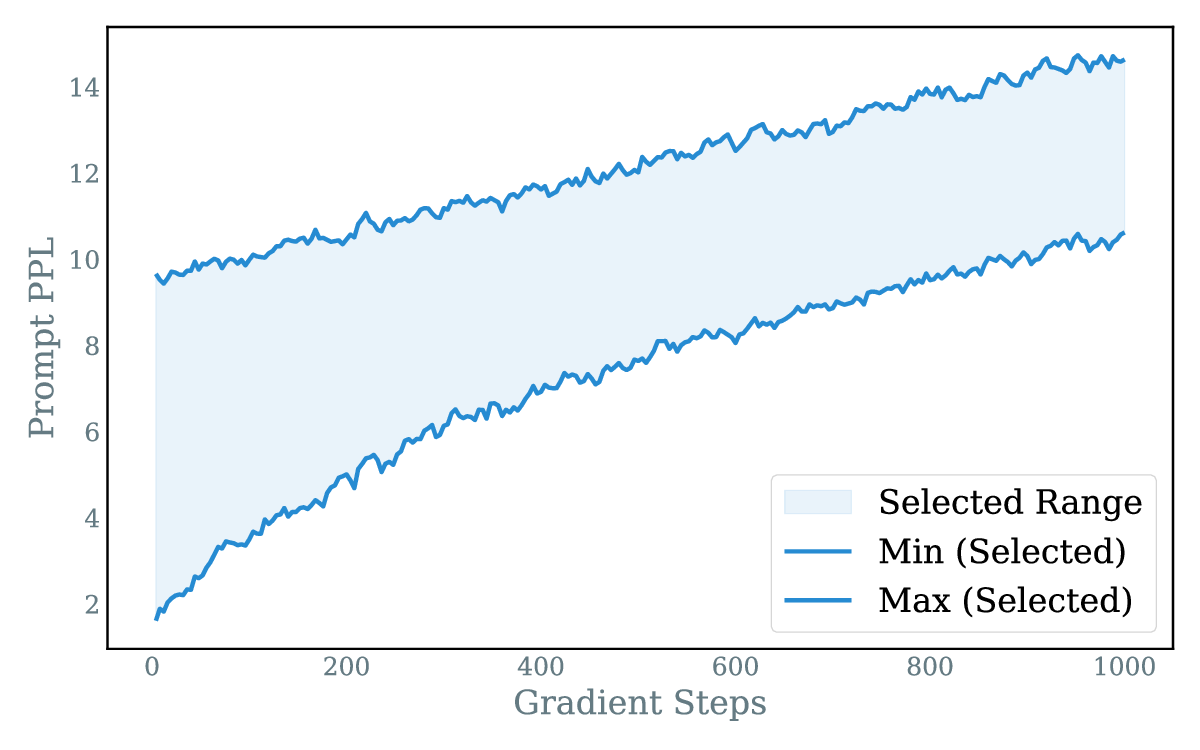
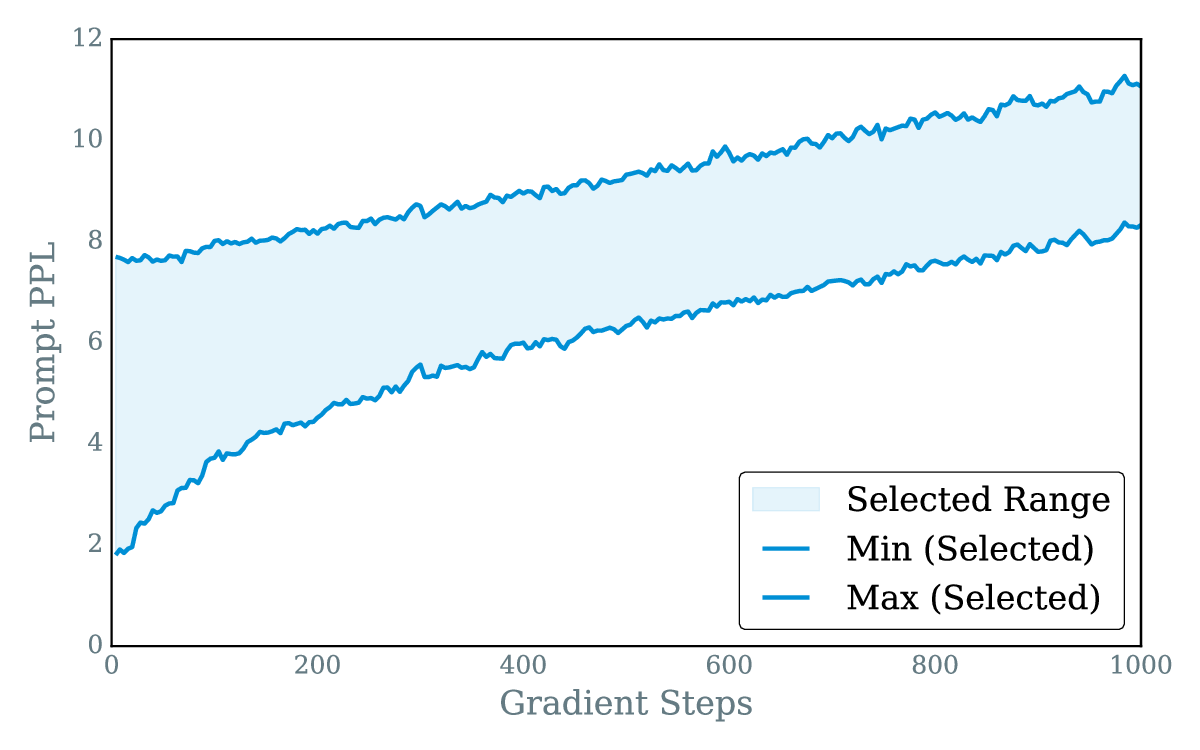
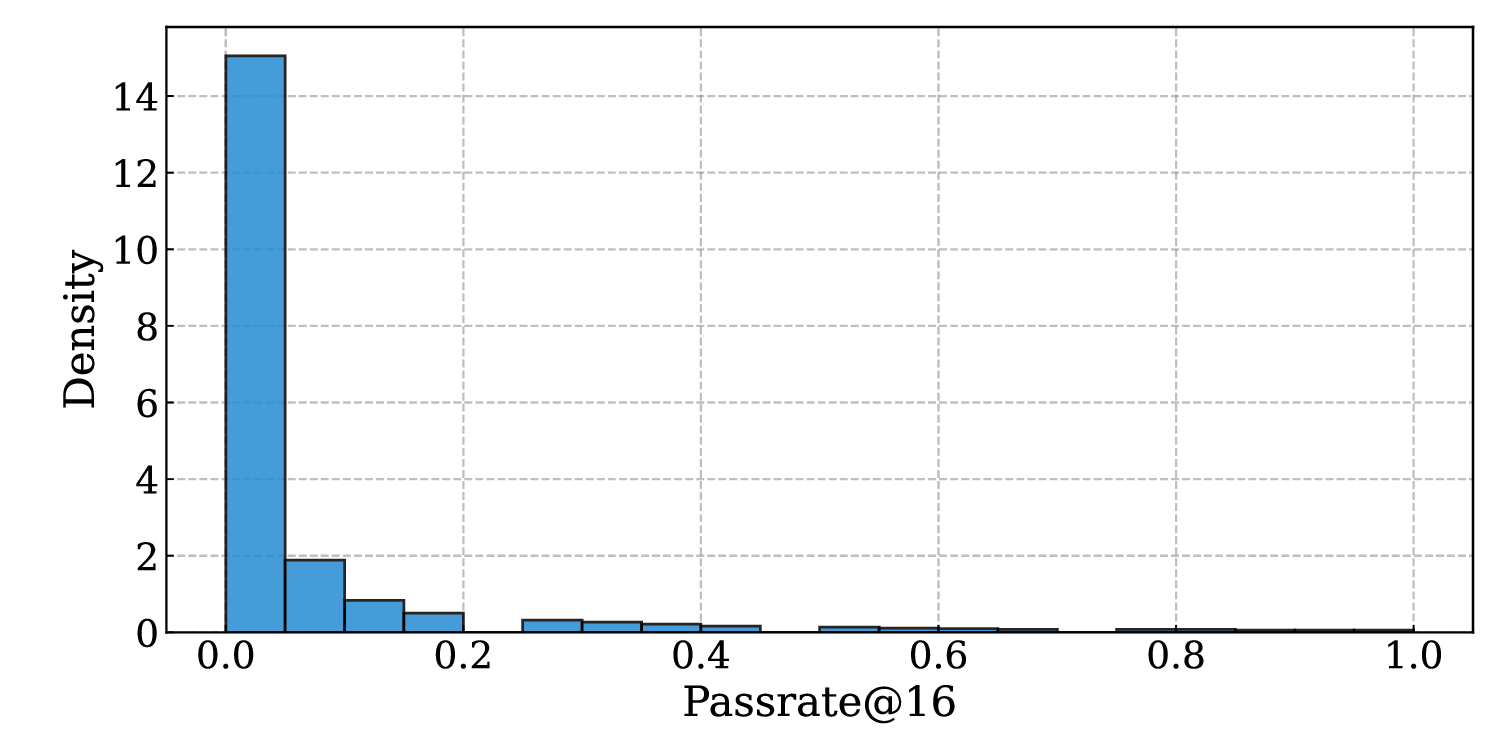
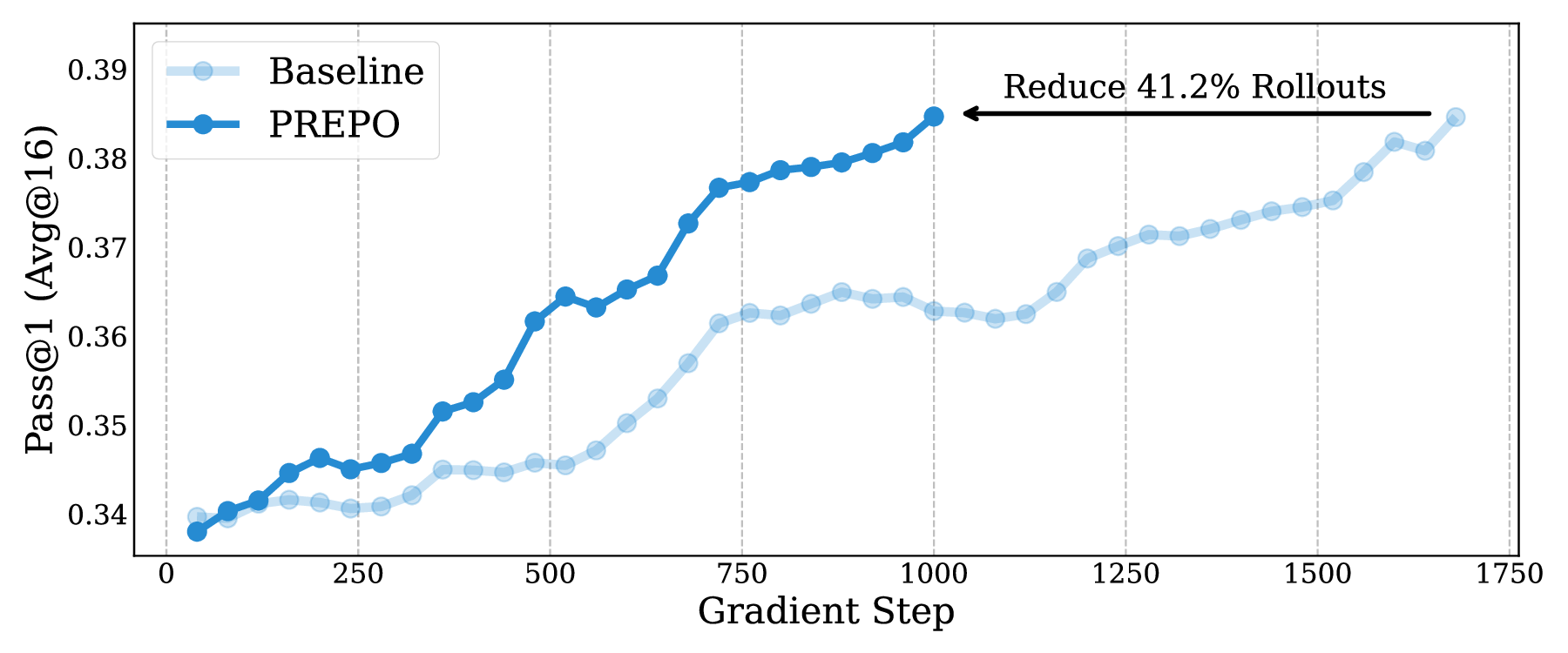
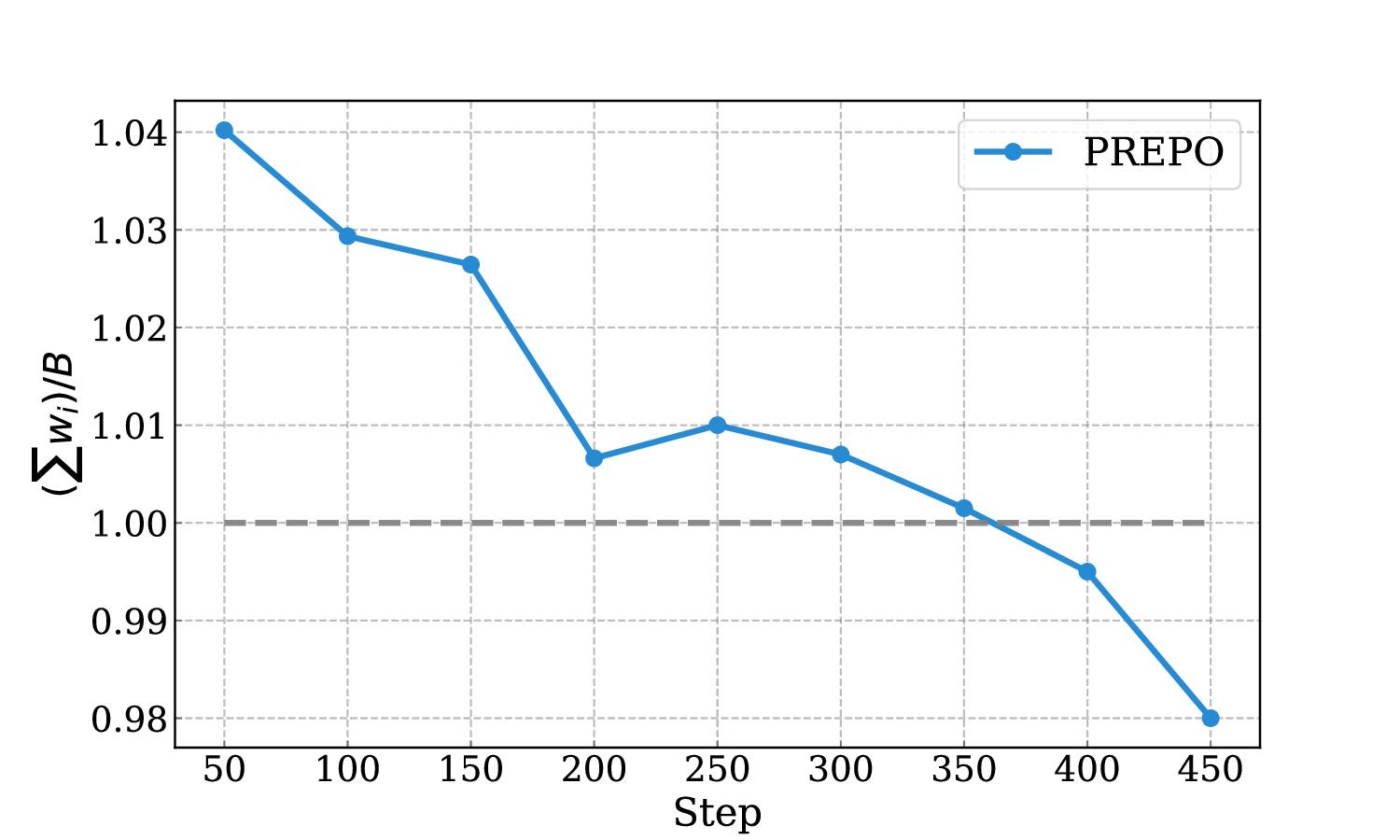
Reinforcement learning with verifiable rewards (RLVR) has improved the reasoning ability of large language models, yet training remains costly because many rollouts contribute little to optimization, considering the amount of computation required. This study investigates how simply leveraging intrinsic data properties, almost free benefit during training, can improve data efficiency for RLVR. We propose PREPO with two complementary components. First, we adopt prompt perplexity as an indicator of model adaptability in learning, enabling the model to progress from well-understood contexts to more challenging ones. Second, we amplify the discrepancy among the rollouts by differentiating their relative entropy, and prioritize sequences that exhibit a higher degree of exploration. Together, these mechanisms reduce rollout demand while preserving competitive performance. On the Qwen and Llama models, PREPO achieves effective results on mathematical reasoning benchmarks with up to 3 times fewer rollouts than the baselines. Beyond empirical gains, we provide theoretical and in-depth analyses explaining the underlying rationale of our method to improve the data efficiency of RLVR.

💡 Deep Analysis

📄 Full Content

📸 Image Gallery

Reference