Efficient Estimation of Regularized Tyler's M-Estimator Using Approximate LOOCV

📝 Original Info

• Title: Efficient Estimation of Regularized Tyler’s M-Estimator Using Approximate LOOCV
• ArXiv ID: 2505.24781
• Date: 2025-05-30
• Authors: ** 정보 없음 (제공된 텍스트에 저자 정보가 포함되어 있지 않음) **

📝 Abstract

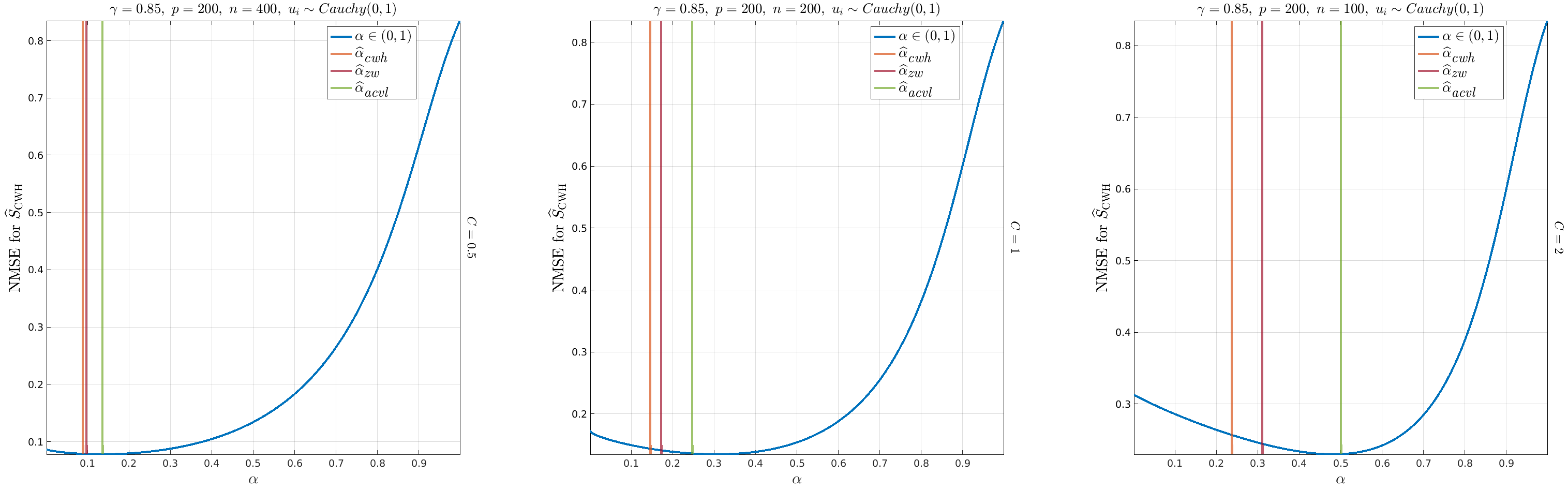
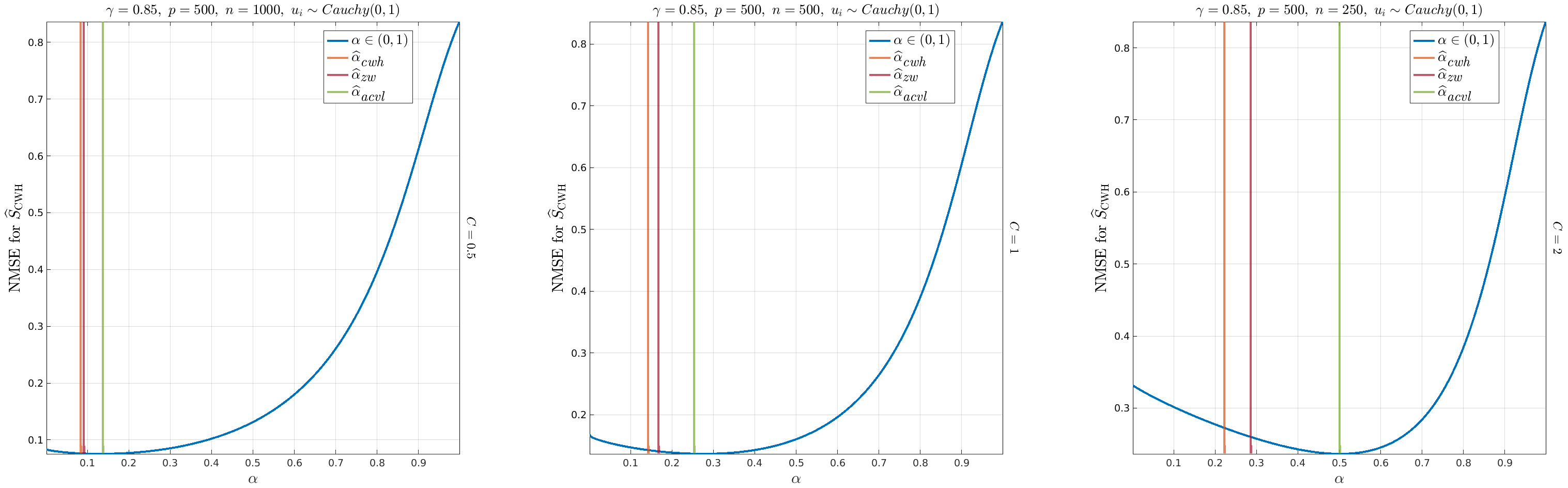
We consider the problem of estimating a regularization parameter, or a shrinkage coefficient $α\in (0,1)$ for Regularized Tyler's M-estimator (RTME). In particular, we propose to estimate an optimal shrinkage coefficient by setting $α$ as the solution to a suitably chosen objective function; namely the leave-one-out cross-validated (LOOCV) log-likelihood loss. Since LOOCV is computationally prohibitive even for moderate sample size $n$, we propose a computationally efficient approximation for the LOOCV log-likelihood loss that eliminates the need for invoking the RTME procedure $n$ times for each sample left out during the LOOCV procedure. This approximation yields an $O(n)$ reduction in the running time complexity for the LOOCV procedure, which results in a significant speedup for computing the LOOCV estimate. We demonstrate the efficiency and accuracy of the proposed approach on synthetic high-dimensional data sampled from heavy-tailed elliptical distributions, as well as on real high-dimensional datasets for object recognition, face recognition, and handwritten digit's recognition. Our experiments show that the proposed approach is efficient and consistently more accurate than other methods in the literature for shrinkage coefficient estimation.

💡 Deep Analysis

📄 Full Content

📸 Image Gallery

Reference