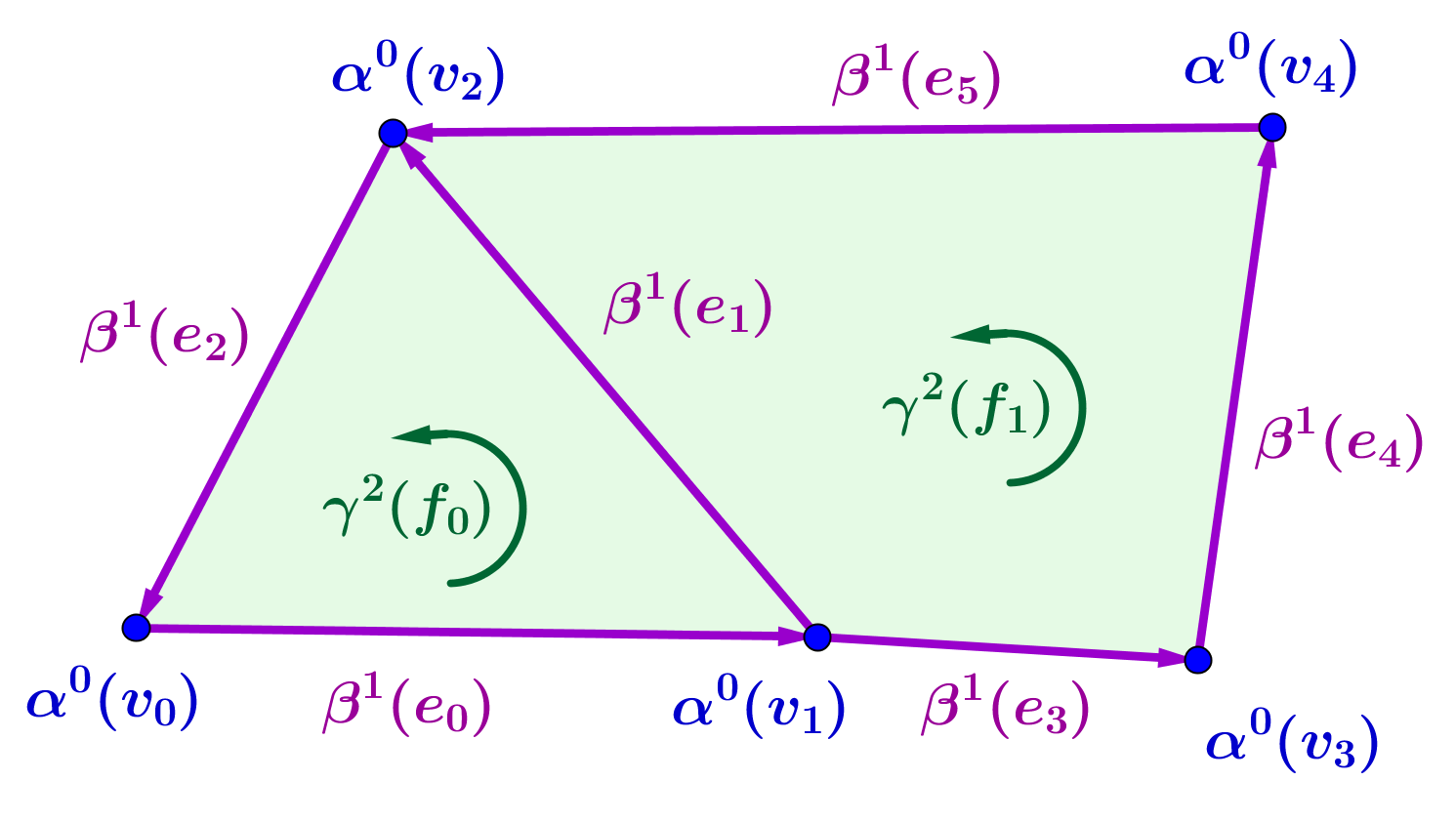
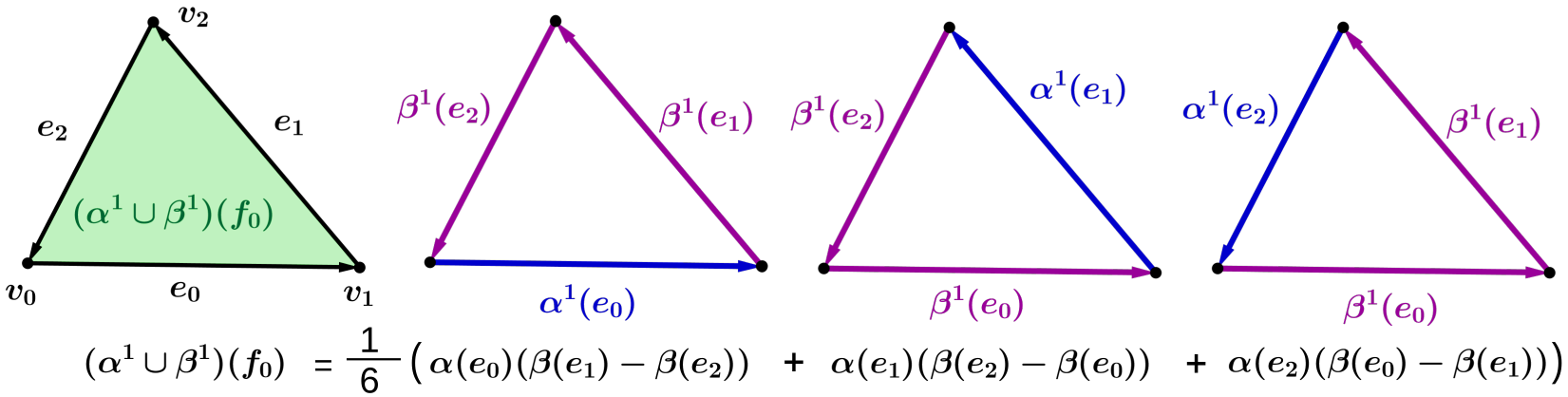A discrete wedge product on general polygonal meshes
📝 Original Info
- Title: A discrete wedge product on general polygonal meshes
- ArXiv ID: 2504.14275
- Date: 2025-04-19
- Authors: Lenka Ptackova
📝 Abstract
Discrete exterior calculus offers a coordinate-free discretization of exterior calculus especially suited for computations on curved spaces. In this work, we present a wedge product on 2-dimensional pseudomanifolds, whose faces are any polygons. We prove that this polygonal wedge product is compatible with the discrete exterior derivative in the sense that it satisfies the Leibniz product rule. We thus extend previously studied discretizations of wedge products from simplicial or quadrilateral meshes to surface meshes whose faces are arbitrary simple polygons. We also prove that our discrete wedge product corresponds to a cup product of cochains on 2-pseudomanifolds. By rigorously justifying our construction we add another piece to ever evolving discrete versions of exterior calculus.💡 Deep Analysis
This research explores the key findings and methodology presented in the paper: A discrete wedge product on general polygonal meshes.Discrete exterior calculus offers a coordinate-free discretization of exterior calculus especially suited for computations on curved spaces. In this work, we present a wedge product on 2-dimensional pseudomanifolds, whose faces are any polygons. We prove that this polygonal wedge product is compatible with the discrete exterior derivative in the sense that it satisfies the Leibniz product rule. We thus extend previously studied discretizations of wedge products from simplicial or quadrilateral meshes to surface meshes whose faces are arbitrary simple polygons. We also prove that our discrete wedge product corresponds to a cup product of cochains on 2-pseudomanifolds. By rigorously justifying our construction we add another piece to ever evolving discrete versions of exterior calculus.
📄 Full Content
📸 Image Gallery