From Interpretability to Inference An Estimation Framework for Universal Approximators

📝 Original Paper Info

- Title: From interpretability to inference an estimation framework for universal approximators
- ArXiv ID: 1903.04209
- Date: 2024-12-06
- Authors: Andreas Joseph

📝 Abstract

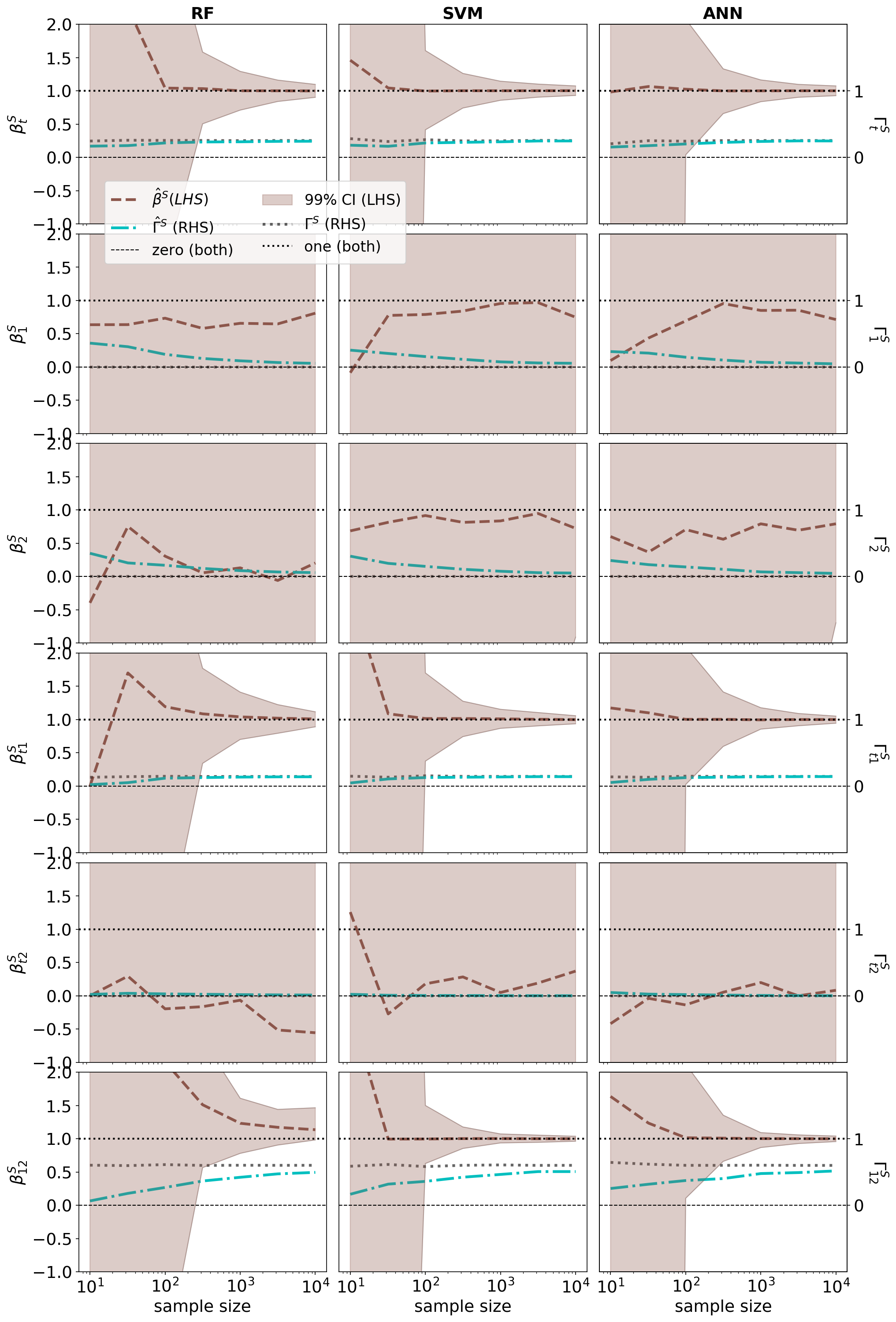
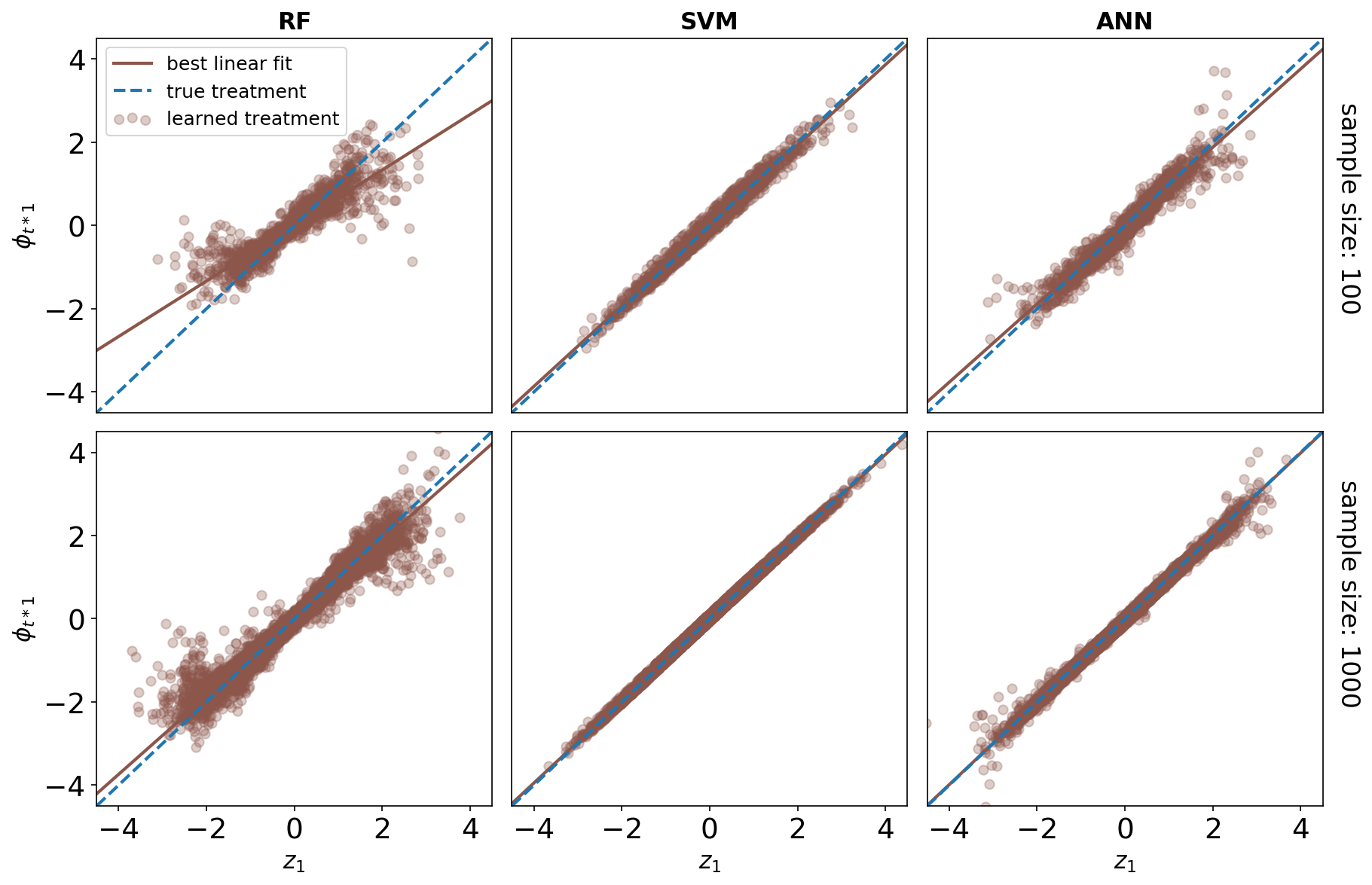
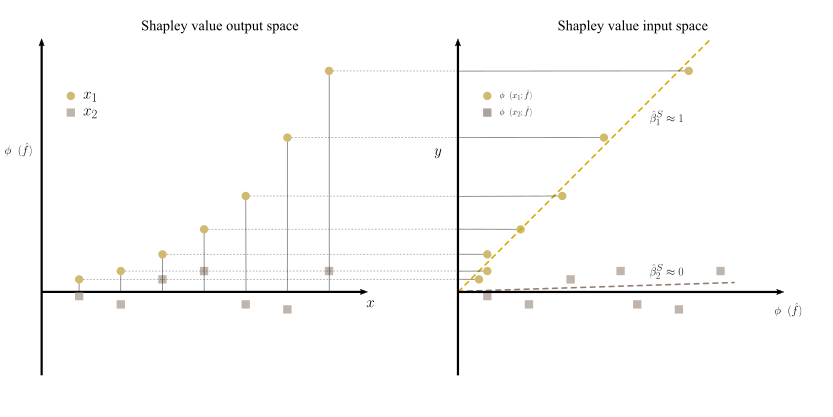
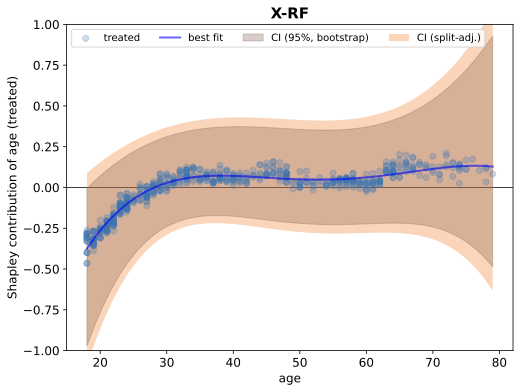
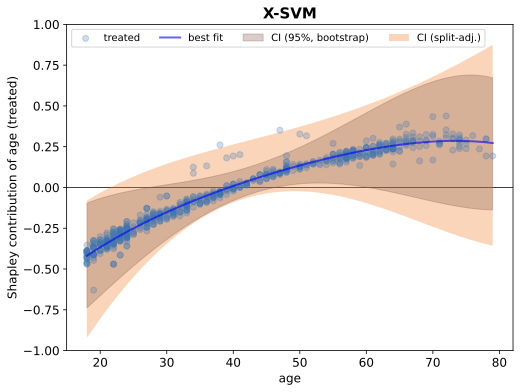
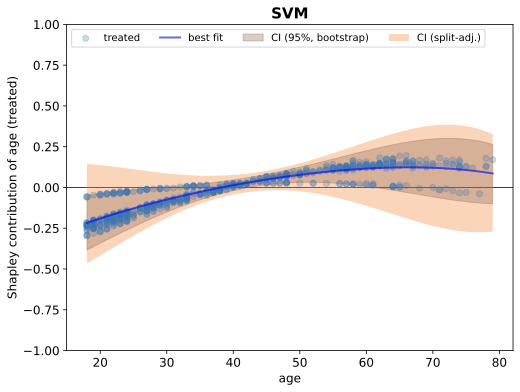
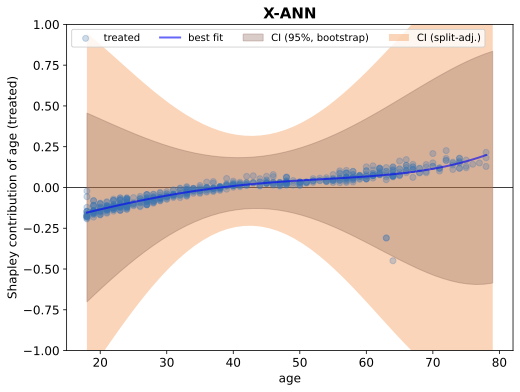
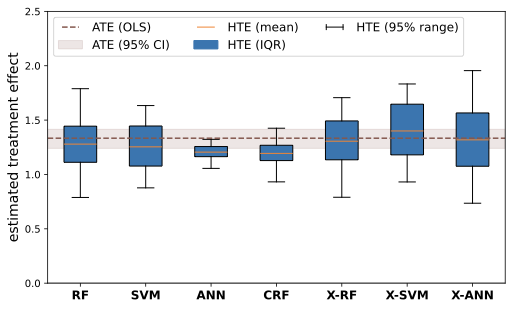
We present a novel framework for estimation and inference with the broad class of universal approximators. Estimation is based on the decomposition of model predictions into Shapley values. Inference relies on analyzing the bias and variance properties of individual Shapley components. We show that Shapley value estimation is asymptotically unbiased, and we introduce Shapley regressions as a tool to uncover the true data generating process from noisy data alone. The well-known case of the linear regression is the special case in our framework if the model is linear in parameters. We present theoretical, numerical, and empirical results for the estimation of heterogeneous treatment effects as our guiding example.

💡 Summary & Analysis

This paper introduces a new framework for interpreting and understanding predictions made by complex machine learning models known as universal approximators. The core idea revolves around decomposing model predictions into Shapley values, which are used to measure how much each feature contributes to the final prediction. This approach helps in understanding individual components of the model's bias and variance.

The key contribution of this research is a robust estimation method that ensures Shapley value estimations are asymptotically unbiased. Additionally, it introduces Shapley regressions as a tool for uncovering true data generation processes from noisy data alone. The paper also demonstrates how linear regression can be seen as a special case within their framework when the model parameters are linear.

This work is significant because it bridges the gap between complex machine learning models and interpretability. It allows developers to understand what drives predictions in these models, enabling more informed decision-making based on true underlying data patterns rather than just surface-level trends obscured by noise.

📄 Full Paper Content (ArXiv Source)

📊 논문 시각자료 (Figures)

A Note of Gratitude

The copyright of this content belongs to the respective researchers. We deeply appreciate their hard work and contribution to the advancement of human civilization.