Retrieval-augmented generation (RAG) enables large language models (LLMs) to access external knowledge, helping mitigate hallucinations and enhance domain-specific expertise. Graph-based RAG enhances structural reasoning by introducing explicit relational organization that enables information propagation across semantically connected text units. However, these methods typically rely on Euclidean embeddings that capture semantic similarity but lack a geometric notion of hierarchical depth, limiting their ability to represent abstraction relationships inherent in complex knowledge graphs. To capture both fine-grained semantics and global hierarchy, we propose HyperbolicRAG, a retrieval framework that integrates hyperbolic geometry into graph-based RAG. HyperbolicRAG introduces three key designs: (1) a depth-aware representation learner that embeds nodes within a shared Poincaré manifold to align semantic similarity with hierarchical containment, (2) an unsupervised contrastive regularization that enforces geometric consistency across abstraction levels, and (3) a mutual-ranking fusion mechanism that jointly exploits retrieval signals from Euclidean and hyperbolic spaces, emphasizing cross-space agreement during inference. Extensive experiments across multiple QA benchmarks demonstrate that HyperbolicRAG outperforms competitive baselines, including both standard RAG and graphaugmented baselines.
L ARGE language models (LLMs) have demonstrated re- markable capabilities across a wide range of natural language processing tasks, including question answering, summarization, dialogue generation, and personalization [1], [2], [3]. Despite their strong generalization ability, LLMs inevitably suffer from knowledge staleness and hallucination, as their internal parameters cannot be easily updated with newly emerging facts or domain-specific information [4].
To mitigate these limitations, retrieval-augmented generation (RAG) [5] has emerged as a powerful paradigm that equips LLMs with access to external knowledge bases. By retrieving relevant documents at inference time and conditioning generation on this evidence, RAG systems can provide more up-to-date and contextually grounded responses, thereby reducing reliance on outdated or incomplete parametric knowledge. Building on this idea, graph-based RAG methods, such as G-Retriever [6], GraphRAG [7], LightRAG [8], Hip-poRAG [9] and HippoRAG2 [10], have organized the retrieved or corpus-level documents into graph structures. In these approaches, documents, entities, and concepts are represented as interconnected nodes linked by semantic or relational edges, enabling more structured access to knowledge. This paradigm enables multi-hop evidence aggregation through explicit graph traversal or message passing, thereby improving reasoning over linked knowledge.
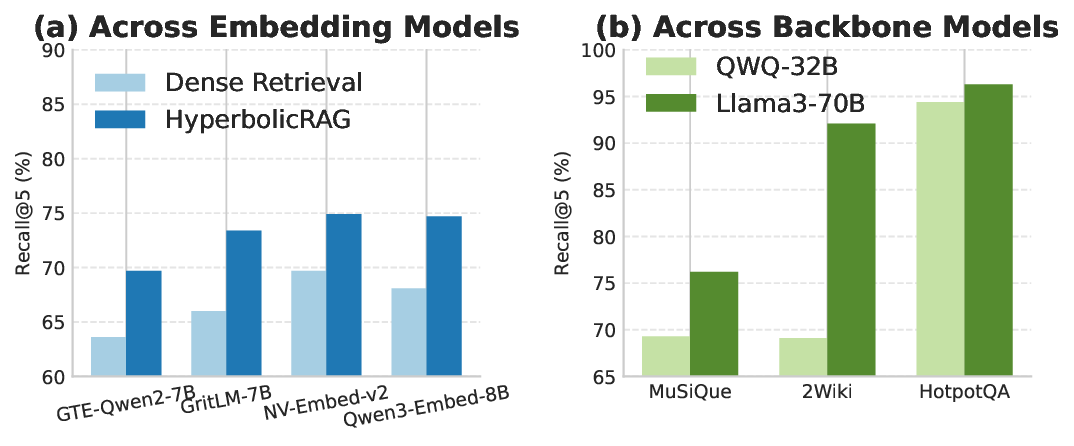
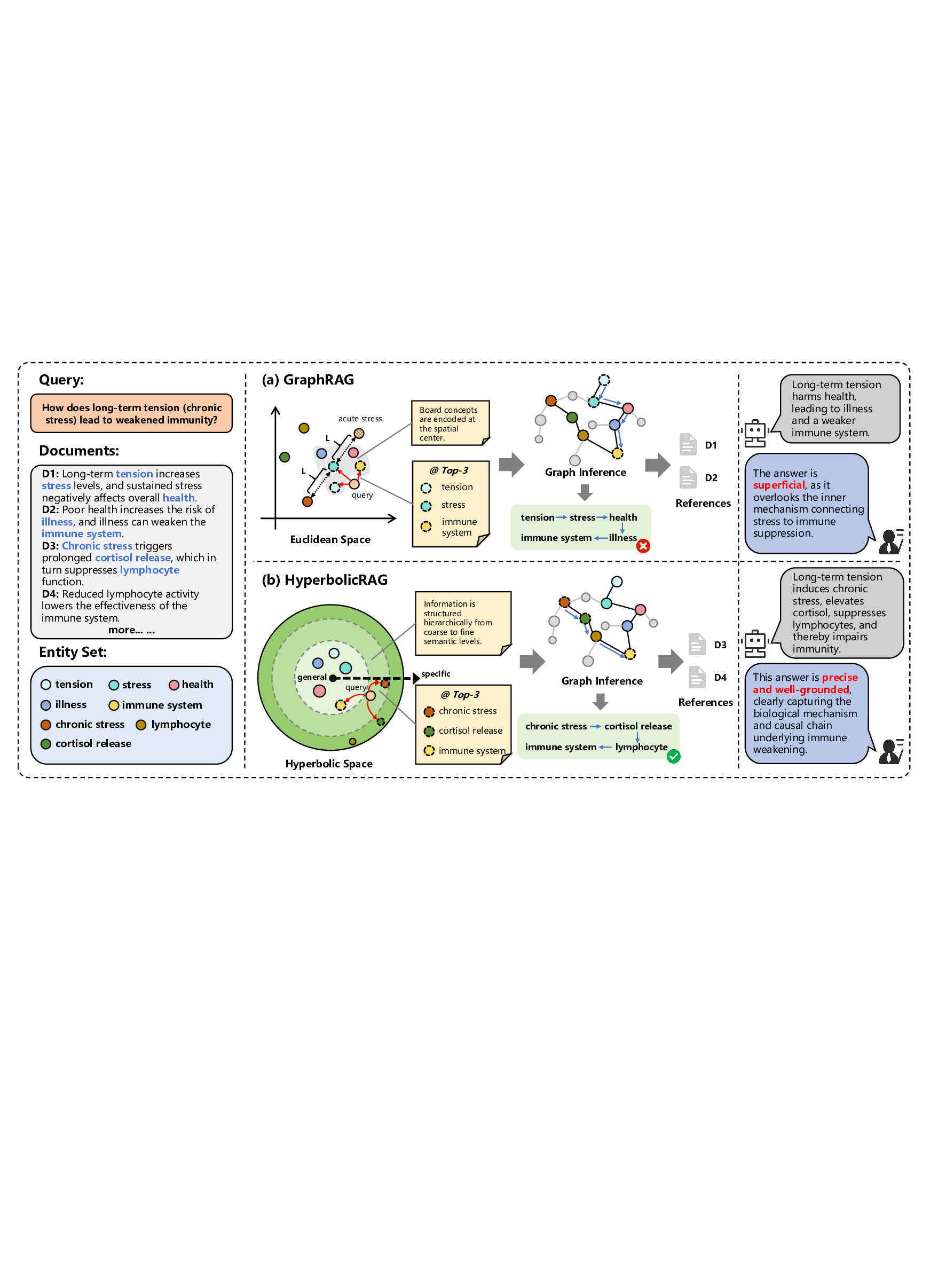
However, graph-based retrieval and reasoning methods typically embed nodes in flat Euclidean spaces, which are ill-suited for representing the hierarchical dependencies that underlie complex knowledge [11], [12]. Consider the query, “How does long-term tension (chronic stress) lead to weakened immunity?” A standard dense retriever 1 usually returns passages about broad themes like “health” or “stress,” which are superficially relevant yet too generic to reflect the underlying mechanisms. This behavior arises from the hubness inherent in high-dimensional Euclidean embedding spaces [14], [15]: semantically broad concepts occupy central regions that lie close to many queries, causing retrieval to disproportionately favor high-frequency, generic nodes. Consequently, graph traversal treats nodes as if they lie on a single semantic plane, overlooking that “cortisol release” is a specific descendant of “stress” along a causal and ontological hierarchy. In other words, graph-based propagation can connect entities while remaining largely insensitive to the hierarchical geometry that structures complex domains.
To address these challenges, and inspired by findings that human perception structures concepts in tree-like hierarchies where general concepts subsume more specific subconcepts [16], we propose integrating hyperbolic geometry into GraphRAG. Hyperbolic geometry naturally models such structures by encoding semantic depth and containment with minimal distortion [17], [18]: radial distance represents levels of specificity, and the exponential expansion of hyperbolic space accommodates large and deep hierarchies. As illustrated in Fig. 1, in Euclidean space (top), general and specific concepts co-locate on a flat surface, limiting the separation of leaf-leaf nodes and blurring hierarchical boundaries. In contrast, within hyperbolic space (bottom), general concepts are positioned near the center, while specific facts are located 1 Dense retrievers encode queries and documents into continuous vector representations and retrieve results based on embedding similarity [13].
Comparison of Euclidean vs. hyperbolic embedding effects on retrieval-augmented multi-hop reasoning. (a) In Euclidean space, embeddings primarily reflect surface-level semantic similarity. high-level concepts (e.g., stress) act as semantic hubs because their vectors approximate the mean of multiple subordinate contexts (e.g., acute stress, chronic stress). Linear distance metrics therefore make these hub nodes geometrically close to many queries, causing top-k activation to favor broad concepts and leading graph propagation (PPR) to spread over general subgraphs. The resulting answers tend to be superficial. (b) In hyperbolic space, hierarchical depth is encoded radially: general concepts concentrate near the center while fine-grained mechanistic facts align near the boundary. A mechanism-oriented query is mapped closer to boundary nodes (via depth alignment), which yields initial activation on specific mechanism nodes (e.g., chronic stress, cortisol release, lymphocyte). Subsequent propagation remains focused within the mechanism subbranch, producing more precise, causal answers. toward the boundary. This arrangement exploits the exponential growth property to preserve hierarchical containment relations.
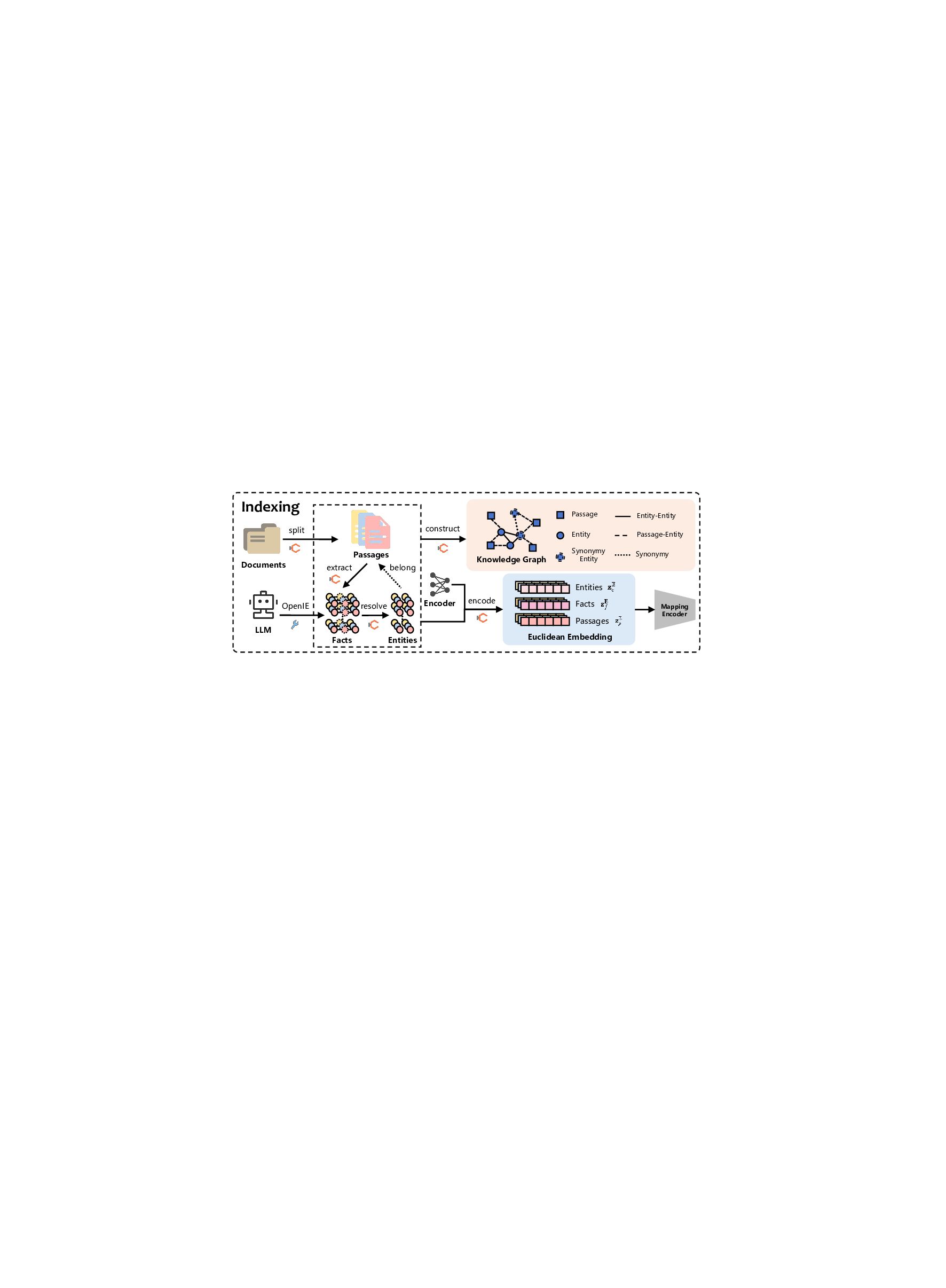
Building upon this geometric insight, we develop Hyperbol-icRAG, a hierarchy-aware retrieval framework that integrates hyperbolic geometry into graph-based RAG. HyperbolicRAG introduces three key components. First, it predicts a semantic depth fo
This content is AI-processed based on open access ArXiv data.