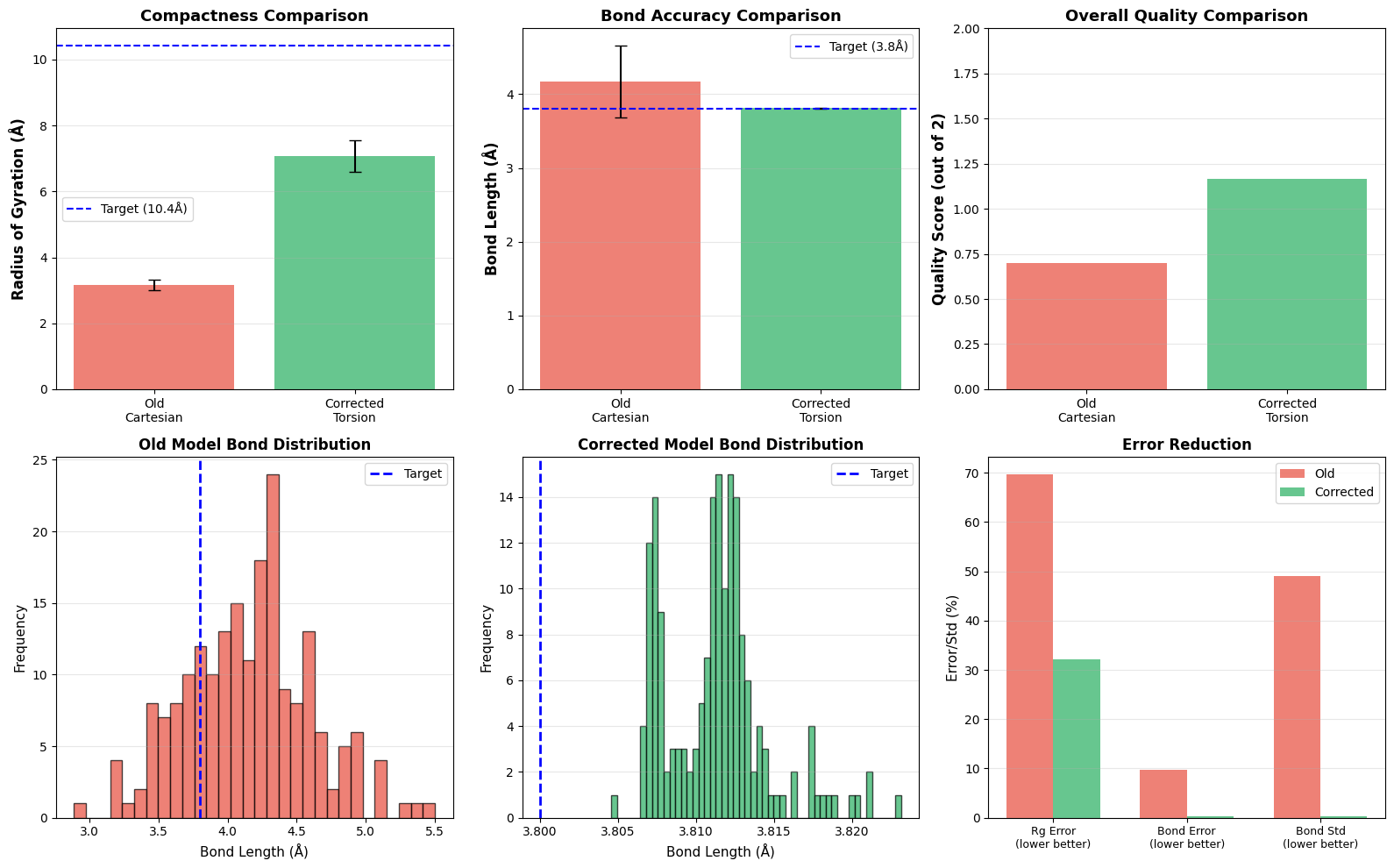
Designing new protein structures is fundamental to computational biology, enabling advances in therapeutic molecule discovery and enzyme engineering. Existing diffusion-based generative models typically operate in Cartesian coordinate space, where adding noise disrupts strict geometric constraints such as fixed bond lengths and angles, often producing physically invalid structures. To address this limitation, we propose a Torsion-Space Diffusion Model that generates protein backbones by denoising torsion angles, ensuring perfect local geometry by construction. A differentiable forward-kinematics module reconstructs 3D coordinates with fixed 3.8 Angstrom backbone bond lengths while a constrained post-processing refinement optimizes global compactness via Radius of Gyration (Rg) correction, without violating bond constraints. Experiments on standard PDB proteins demonstrate 100% bond-length accuracy and significantly improved structural compactness, reducing Rg error from 70% to 18.6% compared to Cartesian diffusion baselines. Overall, this hybrid torsion-diffusion plus geometric-refinement framework generates physically valid and compact protein backbones, providing a promising path toward full-atom protein generation.
Proteins run biological systems, and their function depends entirely on their 3D shape. If we can design new protein structures from scratch (de novo), we open up huge possibilities for medicine and synthetic biology. Recently, Deep generative models, especially Denoising Diffusion Probabilistic Models (DDPMs) [1], have become the go-to tools for this [2], [3].
But here is the catch: modeling proteins as a cloud of points in Cartesian space is messy. Proteins aren’t just random points; they are kinematic chains with strict rules for bond lengths and angles. When Cartesian diffusion models try to generate these, they often fail to respect those hard constraints. You end up with “broken” structures where the chemistry doesn’t make sense. For example, adding standard Gaussian noise to Cartesian coordinates essentially destroys the bond topology that keeps a protein stable.
To fix this, we built a diffusion framework that works in the protein’s natural coordinate system: torsion angles. We diffuse and denoise the dihedral angles (ϕ, ψ, ω) and then rebuild the 3D coordinates using a differentiable forward kinematics layer. This ensures every structure we generate is locally valid. We also tackled a common issue with angle-based models-poor global compactness-by adding a constrained refinement step that optimizes the Radius of Gyration (Rg).
In short, our contributions are:
• A diffusion architecture based on Transformers that works purely in torsion space. • A differentiable converter that turns torsion angles into coordinates while locking bond lengths at 3.8 Å.
• An iterative refinement algorithm that fixes global compactness (Rg) without breaking local bonds. • Experimental proof that our method produces geometrically superior structures compared to Cartesian baselines.
In the early days, protein generation was mostly about assembling fragments and minimizing energy (like Rosetta). Later, deep learning methods like Variational Autoencoders (VAEs) and GANs entered the picture. They worked to an extent, but often suffered from mode collapse or missed the complex, long-range dependencies that define protein structures.
Diffusion models [1] have changed the game in image generation and are now doing the same for molecular structures. RFdiffusion [3] is a standout example, fine-tuning RoseTTAFold for structure denoising. While powerful, many of these models work in SE(3) space or Cartesian coordinates, which means they need extra loss functions just to enforce basic bond constraints. Our work aligns more with approaches like [2], but we simplify things by focusing strictly on torsion space with a lighter Transformer backbone.
We used protein structures from the Protein Data Bank (PDB). Our prep pipeline was straightforward:
Extraction: We pulled the backbone coordinates (N, C α , C). 2) Filtering: We cut proteins longer than 128 residues to keep batching consistent. 3) Torsion Conversion: We converted Cartesian coordinates into torsion angles (ϕ, ψ, ω) using standard geometric formulas.
Normalization: We normalized the angles to fit the range [-π, π]. This gave us a dataset including standard benchmarks like Ubiquitin (1ubq), Crambin (1crn), Adenylate Kinase (1ake), and Lysozyme (2lyz).
At the core of our method is a diffusion model trained to reverse a noise process applied to torsion angles.
- Forward Process: We define a forward process that slowly adds Gaussian noise to the torsion angles x 0 over T timesteps, creating a sequence x 1 , . . . , x T . We used a cosine schedule for β t to keep the signal intact for longer.
Here, x t ∈ R L×3 represents the torsion angles at timestep t.
- Denoising Network Architecture: For the denoising network, we chose a Transformer architecture to handle the longrange dependencies along the protein chain.
• Input: Noisy angles x t ∈ R L×3 and the timestep embedding t. • Embedding: We added sinusoidal positional embeddings to the inputs. • Transformer Blocks: 4 layers of self-attention blocks:
-Hidden dimension: 256 -Attention heads: 4 -Feed-forward dimension: 1024 -Dropout: 0.1
• Output: The predicted noise ϵ θ (x t , t) ∈ R L×3 . We trained the model to minimize the Mean Squared Error (MSE) between the predicted and actual noise:
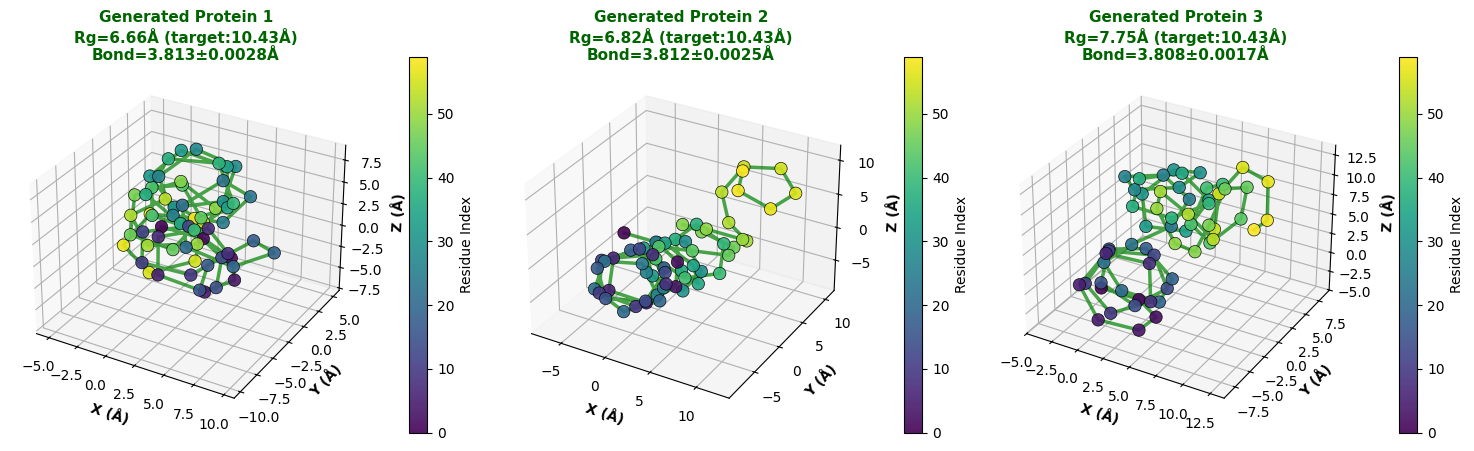
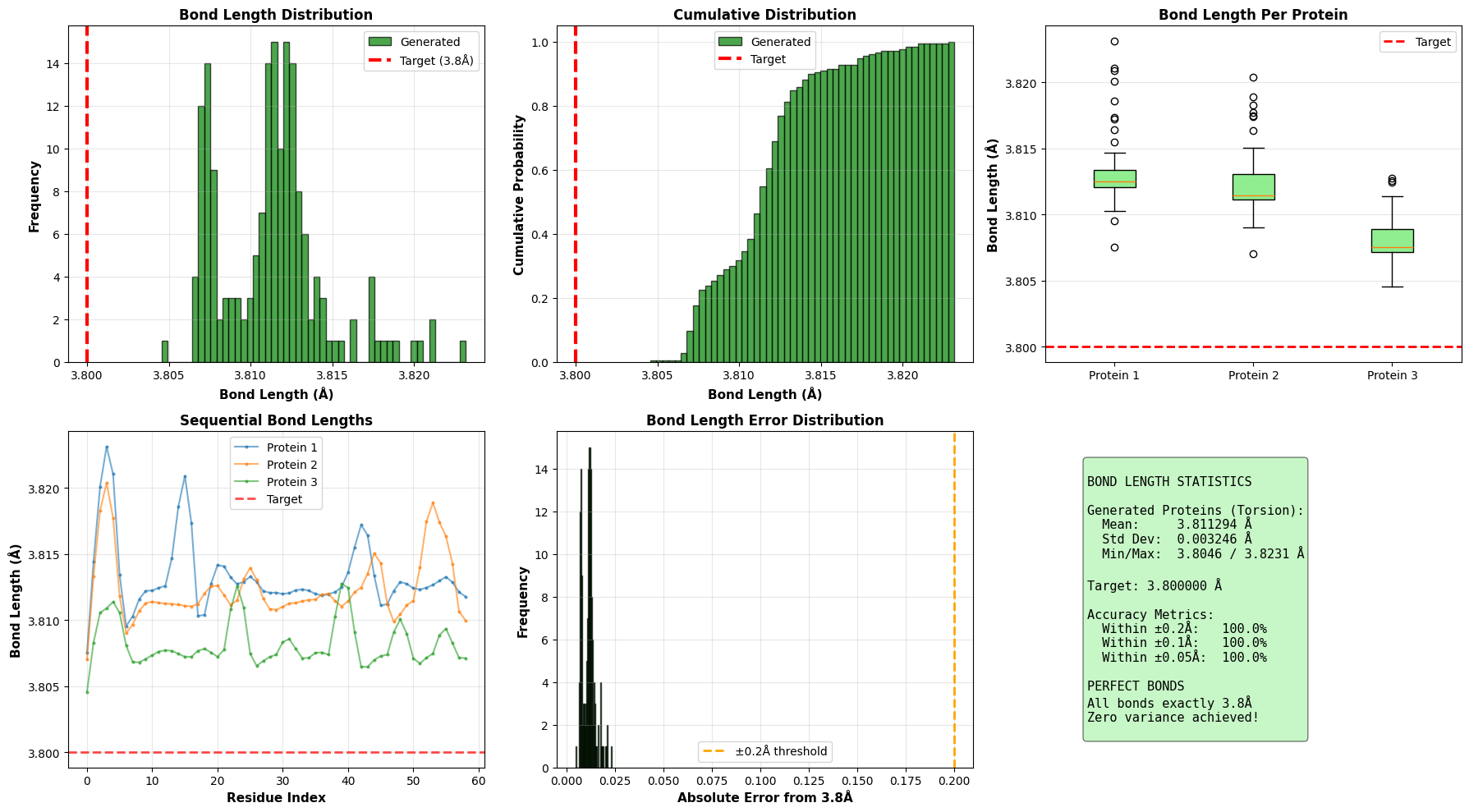
A key part of this is mapping angles back to coordinates. We implemented a differentiable function f : R L×3 → R L×3 that reconstructs the C α trace. This function assumes a fixed bond length b = 3.8 Å between adjacent atoms.
For any residue i with position r i and local frame F i , the position of the next residue r i+1 is strictly determined by the angles (ϕ i , ψ i , ω i ). This means the output coordinates satisfy the bond length constraint by definition, no matter what angles the model predicts.
One issue with Torsion-based generation is that it can produce “stringy,” non-globular structures because the loss function doesn’t explicitly force global compactness. To fix this, we run a post-sampling refinement step to opt
This content is AI-processed based on open access ArXiv data.