Optimal Investment under Correlated Random Volatility Factors
📝 Original Paper Info
- Title: Optimal Investment with Correlated Stochastic Volatility Factors- ArXiv ID: 1908.07626
- Date: 2022-11-29
- Authors: Maxim Bichuch and Jean-Pierre Fouque
📝 Abstract
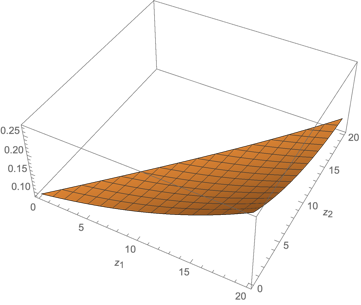
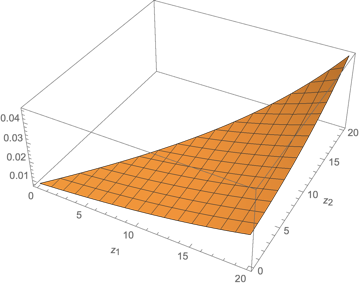
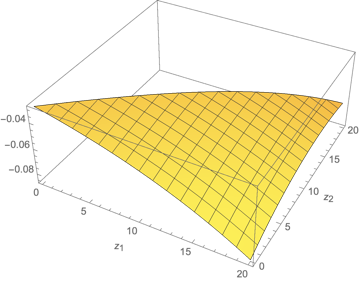
The problem of portfolio allocation in the context of stocks evolving in random environments, that is with volatility and returns depending on random factors, has attracted a lot of attention. The problem of maximizing a power utility at a terminal time with only one random factor can be linearized thanks to a classical distortion transformation. In the present paper, we address the situation with several factors using a perturbation technique around the case where these factors are perfectly correlated reducing the problem to the case with a single factor. Our proposed approximation requires to solve numerically two linear equations in lower dimension instead of a fully non-linear HJB equation. A rigorous accuracy result is derived by constructing sub- and super- solutions so that their difference is at the desired order of accuracy. We illustrate our result with a particular model for which we have explicit formulas for the approximation. In order to keep the notations as explicit as possible, we treat the case with one stock and two factors and we describe an extension to the case with two stocks and two factors.💡 Summary & Analysis
This paper presents a novel approach to determining optimal investment in an environment with multiple stochastic volatility factors where stock values and returns vary unpredictably over time. The research aims to solve the problem of portfolio allocation in such complex systems, where each factor is interconnected and significantly influences investment outcomes. To address this issue, the researchers use a perturbation technique that approximates the multi-factor scenario by starting from a perfectly correlated single-factor case and then making small adjustments. This allows for simplifying calculations through linear equations instead of dealing with complex nonlinear ones. The primary achievement lies in proposing a method to solve two linear equations to approximate the original problem, which is rigorously verified using sub- and super-solutions. This approach holds significant potential for optimizing investment strategies in complex financial environments and can be particularly useful for market analysis and developing robust investment plans.📄 Full Paper Content (ArXiv Source)
📊 논문 시각자료 (Figures)