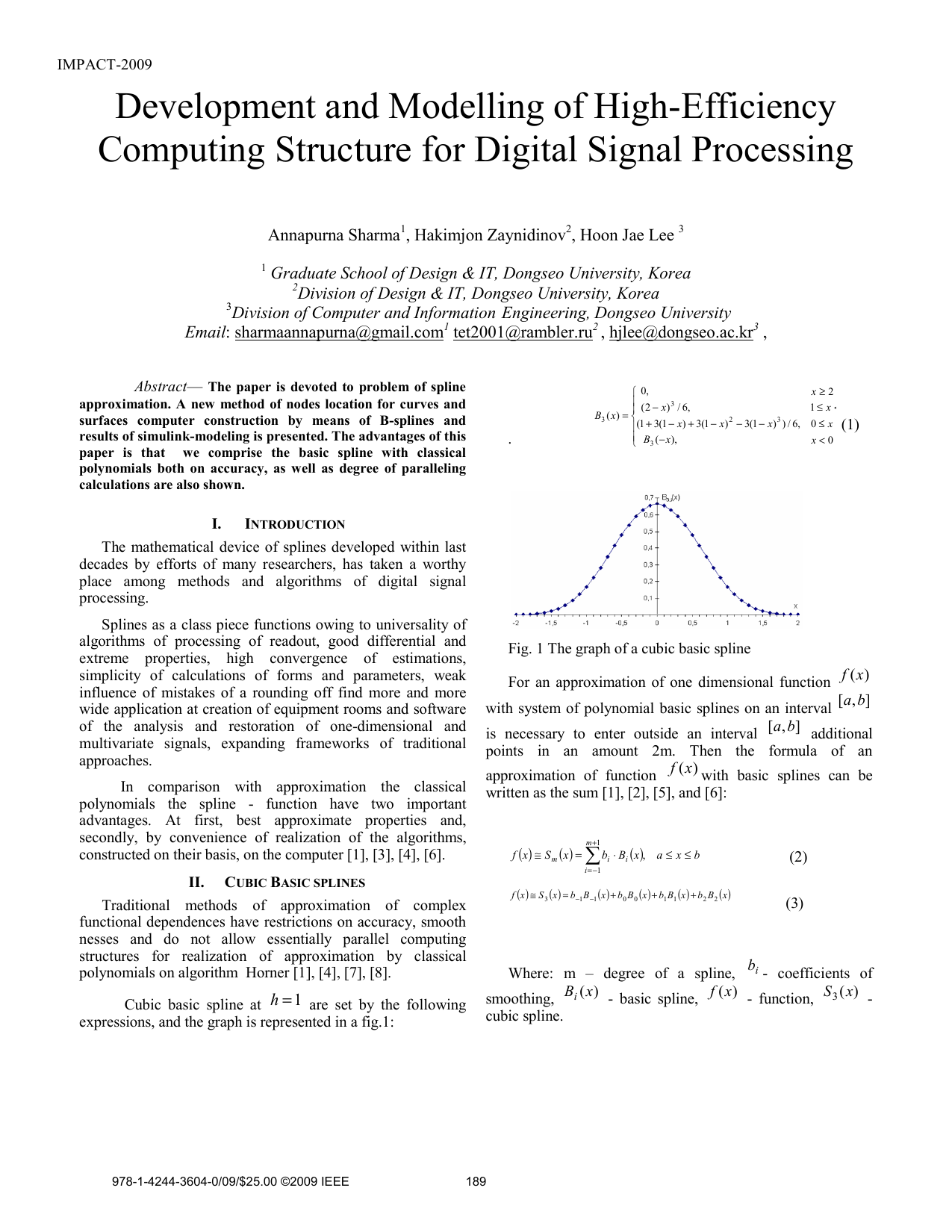
The paper is devoted to problem of spline approximation. A new method of nodes location for curves and surfaces computer construction by means of B-splines and results of simulink-modeling is presented. The advantages of this paper is that we comprise the basic spline with classical polynomials both on accuracy, as well as degree of paralleling calculations are also shown.
The mathematical device of splines developed within last decades by efforts of many researchers, has taken a worthy place among methods and algorithms of digital signal processing.
Splines as a class piece functions owing to universality of algorithms of processing of readout, good differential and extreme properties, high convergence of estimations, simplicity of calculations of forms and parameters, weak influence of mistakes of a rounding off find more and more wide application at creation of equipment rooms and software of the analysis and restoration of one-dimensional and multivariate signals, expanding frameworks of traditional approaches.
In comparison with approximation the classical polynomials the spline -function have two important advantages. At first, best approximate properties and, secondly, by convenience of realization of the algorithms, constructed on their basis, on the computer [1], [3], [4], [6].
Traditional methods of approximation of complex functional dependences have restrictions on accuracy, smooth nesses and do not allow essentially parallel computing structures for realization of approximation by classical polynomials on algorithm Horner [1], [4], [7], [8]. with basic splines can be written as the sum [1], [2], [5], and [6]:
Where: m -degree of a spline, i b -coefficients of smoothing,
The three-dot formula, in this case for calculation of coefficient participate r-1, r and r+1-th values of function ) 8 ( 61
Here r f the reduced form of ) (x f r . Thus, the local properties of basis is appears, and the structure can be created according to tabular -algorithmic methods.
The formula (3) follows, that it is necessary to summarize pair products by groups till four and periodically to update these sums in a summator.
The block scheme (fig. 2) consists of a pre-set block, clock pulse generator (GEN), address counter (СT), generator of b-coefficients, shift register, memory (MEM) consisting of four subsections (ROM1, ROM2, ROM3, ROM4) for storage of value of a basic spline, four multipliers (M) and summator (SUM). ROM2 -01 for an interval
ROM3 -10 for an interval
ROM4 -11 for an interval
The values of b-coefficient are worked out on the generator of b-coefficients with the formula ( 4) and records to the shift register accordingly by blocks . , , ,
The methodical error of interpolation of function Apparently from ( 6), the error exceeds the size received in (7), more than three times.
V. CONCLUSION Thus, (fig. 3.) the high-efficiency computing structure is developed for restoration of the signals. A modeling of the structure using MATLAB simulink environment shows a high efficiency both in terms of the speed and the error. It functions three times more quickly than the existing, and the methodical error of the existing device exceeds three times, than an error of offered structure.
978-1-4244-3604-0/09/$25.00 ©2009 IEEE
This content is AI-processed based on open access ArXiv data.