LLM 엔지니어링 방정식 해결 가능성 직접 예측과 솔버 연동 비교
📝 원문 정보
- Title: Can Large Language Models Solve Engineering Equations? A Systematic Comparison of Direct Prediction and Solver-Assisted Approaches
- ArXiv ID: 2601.01774
- 발행일: 2026-01-05
- 저자: Sai Varun Kodathala, Rakesh Vunnam
📝 초록 (Abstract)
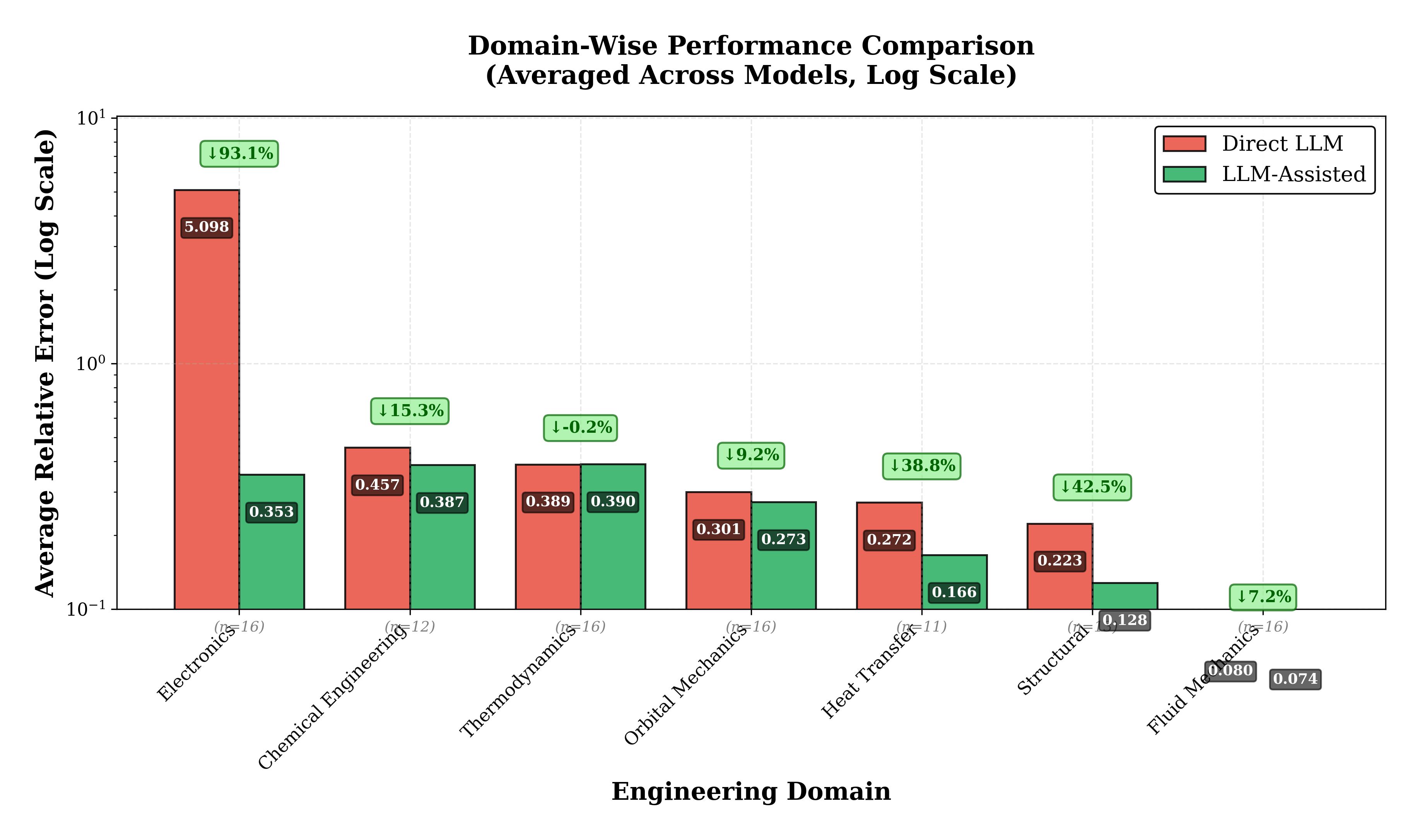
공학 현장에서 마찰계수 계산부터 궤도 위치 추정에 이르기까지 반복적인 수치 해법이 필요한 초월 방정식이 널리 사용된다. 본 연구는 대형 언어 모델(LLM)이 이러한 방정식을 직접 수치 예측으로 해결할 수 있는지, 혹은 LLM이 기호 조작을 수행하고 고전적 반복 솔버와 결합된 하이브리드 구조가 더 효과적인지를 체계적으로 평가한다. 7개 공학 분야에 걸친 100개의 문제에 대해 최신 모델 6종(GPT‑5.1, GPT‑5.2, Gemini‑3‑Flash, Gemini‑2.5‑Lite, Claude‑Sonnet‑4.5, Claude‑Opus‑4.5)을 테스트했으며, 직접 예측 방식과 LLM이 방정식을 구성·초기값을 제공하고 뉴턴‑라프슨 방식으로 수치 해를 구하는 솔버‑보조 방식을 비교하였다. 직접 예측은 모델별 평균 상대 오차가 0.765 %에서 1.262 %인 반면, 솔버‑보조 방식은 0.225 %에서 0.301 %로 오류 감소율이 67.9 %에서 81.8 %에 달한다. 분야별 분석에서는 지수 방정식에 민감한 전자공학에서 93.1 %의 개선 효과가 두드러진 반면, 패턴 인식에 강한 유체역학에서는 7.2 %에 그치는 등 차이를 보였다. 결과는 최신 LLM이 기호 처리와 도메인 지식 검색에서는 뛰어나지만, 정밀한 반복 연산에서는 한계가 있음을 시사한다. 따라서 LLM은 독립적인 계산 엔진보다는 전통적인 수치 해석기와 결합된 지능형 인터페이스로 활용하는 것이 최적이다.💡 논문 핵심 해설 (Deep Analysis)
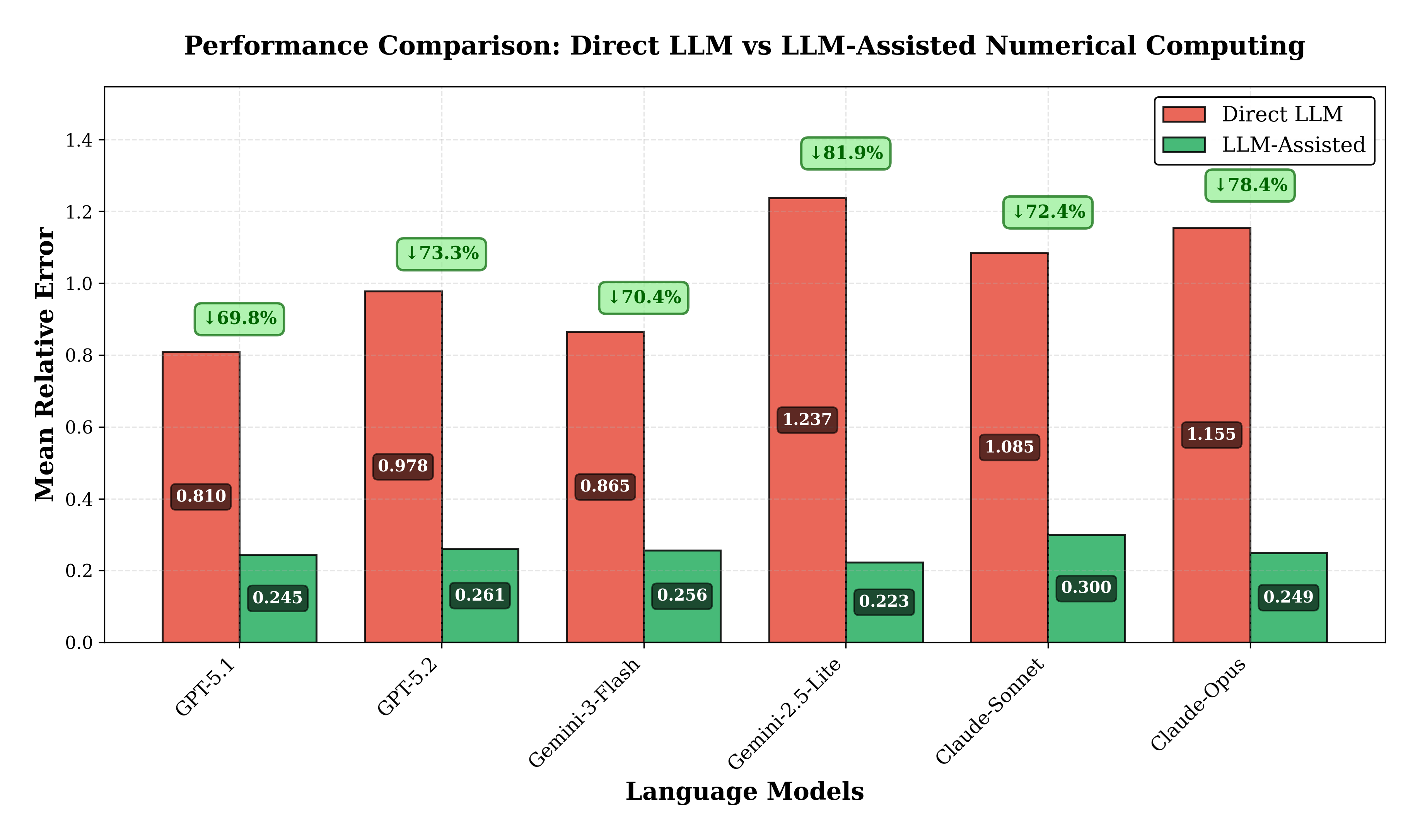
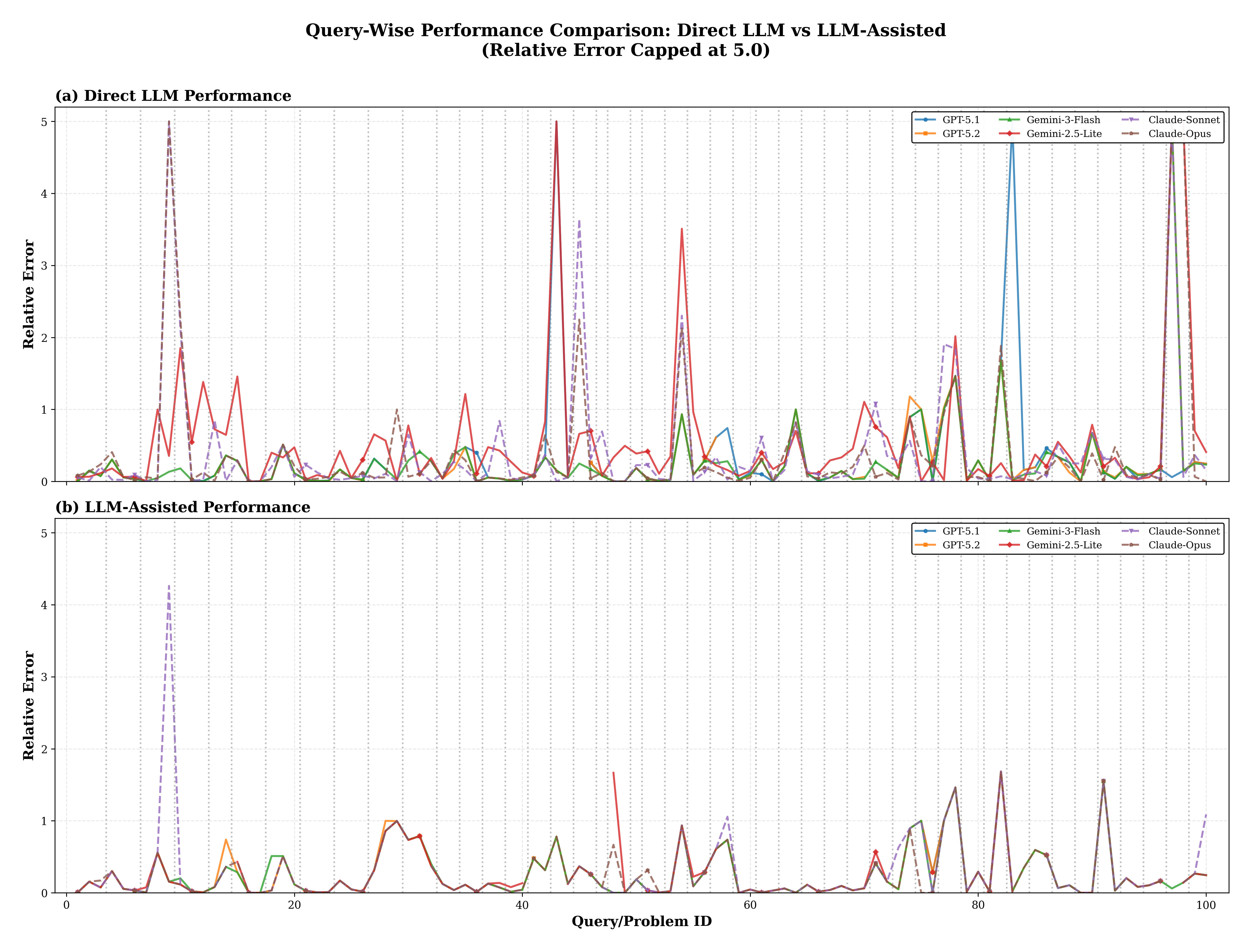
모델별 성능 차이를 살펴보면, 최신 GPT‑5 시리즈와 Claude‑Opus가 상대적으로 낮은 오류를 보였으며, Gemini‑3‑Flash와 Claude‑Sonnet은 약간 높은 편이었다. 이는 각 모델의 훈련 데이터 구성과 수치 연산에 대한 사전 학습 정도가 차이를 만든 것으로 추정된다. 도메인별 분석에서는 전자공학 분야의 지수·로그 형태 방정식이 LLM의 패턴 인식만으로는 높은 민감도를 보이기 때문에 직접 예측에서 큰 오류가 발생했으며, 솔버‑보조를 통해 93 % 이상의 오류 감소가 관찰되었다. 반면 유체역학 분야의 다항식이나 경험식 기반 방정식은 모델이 기존 사례를 기억하고 유사한 형태를 재생산하는 데 강점을 보여, 직접 예측에서도 비교적 낮은 오류(7 % 수준)만을 기록했다.
이러한 결과는 LLM이 “지식 검색·기호 조작” 단계에서는 뛰어나지만, “정밀 수치 연산” 단계에서는 아직 한계가 있음을 명확히 보여준다. 특히 뉴턴‑라프슨과 같은 고전적 반복법은 수렴성 보장과 미세 조정이 가능하므로, LLM이 제공하는 초기값과 방정식 형태만으로도 전체 파이프라인의 효율을 크게 향상시킬 수 있다. 따라서 실무에서는 LLM을 “스마트 프론트엔드”로 활용해 문제 정의, 변수 선정, 초기 추정 등을 자동화하고, 백엔드에서는 검증된 수치 해석기를 그대로 두는 하이브리드 구조가 가장 현실적이다. 향후 연구에서는 LLM이 자체적으로 수치 미분·적분을 수행하도록 훈련시키거나, 자동 미분 프레임워크와 연계해 완전한 엔드‑투‑엔드 솔루션을 모색할 필요가 있다. 또한, 오류 전파와 불확실성 추정 메커니즘을 도입해 LLM이 제공하는 초기값의 신뢰도를 정량화한다면, 설계 단계에서의 위험 관리에도 크게 기여할 수 있을 것이다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리