style="width:100.0%" />

대형 언어 모델(LLMs)의 확장은 트랜스포머와 전문가 혼합(MoE) 아키텍처를 결합함으로써 크게 진보했습니다. 이는 희소 활성화를 통해 계산 비용이 비례적으로 증가하지 않음에도 불구하고 모델 용량을 늘리는 방법입니다. 라우터 네트워크(또는 “라우터”)는 각 입력 토큰에 대해 소수의 전문가들을 동적으로 활성화합니다. 그러나 MoE 모델의 효과는 그 라우팅 결정의 질에 크게 의존합니다.

표준 라우터는 은닉 상태를 기반으로 전문가 할당을 예측하도록 훈련된 가벼운 파라미트릭 분류기입니다. 한 번 훈련이 완료되면 라우터는 고정된 정책을 구현합니다. 내분포 데이터에서는 효과적일 수 있지만, 추론 중에 라우팅 결정을 조정할 유연성이 부족합니다. 입력 데이터가 훈련 분포에서 벗어나면(종종 복잡도가 높은 경우) 라우터는 고정된 사전 지식에서 외삽해야 하며, 이로 인해 비효율적인 전문가를 선택할 수 있습니다. 이러한 유연성 부족은 MoE 모델의 잠재력을 제한하며 특히 특수하거나 분포 외의 작업에서는 더욱 그렇습니다.

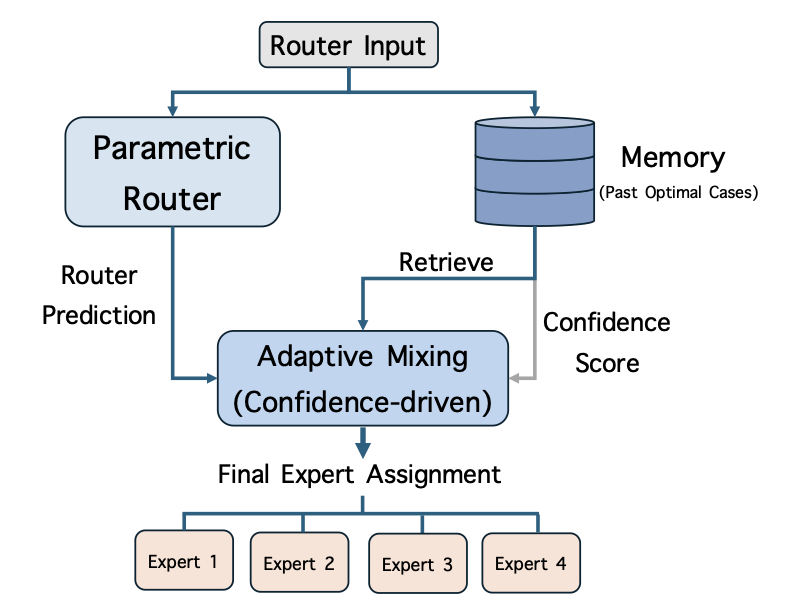
이 논문에서 우리는 kNN-MoE를 제안합니다. 이는 과거 라우터 입력의 가장 가까운 이웃을 검색하고 이를 활용하여 최적의 전문가 할당을 재사용함으로써 라우팅 결정을 정교하게 만듭니다(그림 1). 구체적으로, 우리는 라우터 입력(key)과 참조 집합에서 최대 가능성(maximizing the likelihood on a reference set)을 통해 얻은 최적의 전문가 할당(value)을 저장하는 메모리를 구축합니다. 테스트 시 kNN-MoE는 메모리에서 과거 사례 가능성을 높게 만든 이웃의 전문가 할당을 검색하고 이를 라우터 예측과 결합합니다. 유사도를 신뢰도 점수로 사용하여 이 작업을 수행합니다. 직관적으로, 검색된 이웃이 매우 유사할 때는 검색된 라우팅에 신뢰하고 그렇지 않으면 원래의 파라미트릭 라우터로 돌아가서 관계 없는 검색으로부터 발생하는 잡음을 피합니다.

kNN-MoE를 OLMoE, GPT-OSS 및 Qwen3 등 세 가지 MoE 모델에서 GPQA, SuperGPQA, MMLU, 의학 작업(USMLE와 MedMCQA) 등의 벤치마크에 평가했습니다. 실증 결과 kNN-MoE는 제로샷 기준선보다 우수한 성능을 보였으며, 계산 비용이 상당히 높은 지도 학습 세부 조정과 경쟁하는 성능을 달성하였습니다. 이 모든 것이 모델 파라미터를 수정하지 않고 이루어졌습니다. 궁극적으로 kNN-MoE는 정적인 파라미트릭 라우팅과 동적 추론 요구 사항 사이의 간격을 메우며, 세부 조정의 계산 부담 없이 MoE 모델의 적응성을 향상시키는 확장 가능한 경로를 제공합니다.

관련 작업

MoE의 전문가 할당 최적화

기존 연구에 따르면 MoE에서 전문가 할당을 최적화하면 모델 성능이 향상됩니다. 예를 들어, C3PO는 모델이 올바르게 답변한 예제를 사용하여 라우팅 로짓을 세부 조정하는 테스트 시 적응 방법을 제안했습니다. 그러나 이 접근법은 기준선보다 약 5배 더 큰 계산 비용을 초래합니다.

또한 동시 작업에는 라우터에 보조 손실(auxiliary loss)로 세부 조정하는 것을 포함합니다. 우리의 비파라미트릭 접근과 달리 그들의 방법은 모델이 고정된 채로 남아 있는 반면, 라우터 파라미터를 영구적으로 업데이트합니다. 유사하게, 테스트 시 적응 프레임워크는 입력 컨텍스트에서 자기 지도 손실을 최소화함으로써 전문가 할당을 실시간으로 최적화합니다. 반면에 우리의 프레임워크는 온라인 최적화 오버헤드를 피하고 메모리 저장소에서 캐시된 최적의 할당을 직접 검색하여 사용합니다.

비파라미트릭 및 검색 강화 LM

우리의 작업은 외부 데이터 저장소로 신경망을 보강하는 비파라미트릭 방법과 밀접한 관련이 있습니다. 연구의 한 가지 주요 추세는 캐시된 은닉 상태 데이터 스토어에서 가장 가까운 이웃 토큰을 검색하여 최종 출력 분포를 보간하는 kNN-LM입니다. 유사하게, 검색 강화 생성 모델은 텍스트 조각을 검색하여 생성 과정을 조건으로 합니다. 또한 reranking에서 과거의 고유용도 결정을 검색하여 출력 선택을 안내했습니다.

전문가 혼합

$`L`$ 층이 있는 MoE 트랜스포머 모델을 고려합니다. 여기서 $`\mathcal{L}_{\text{MoE}} \subset \{1, \dots, L\}`$은 MoE 층의 인덱스 집합입니다. 특정 층 $`\ell \in \mathcal{L}_{\text{MoE}}`$에 대해 모듈은 $`N`$ 개의 전문가 네트워크 $`\{E^{(\ell)}_i\}_{i=1}^N`$ 및 라우터 $`R^{(\ell)}`$를 포함합니다.

$`x^{(\ell)} \in \mathbb{R}^d`$는 MoE 모듈의 입력 은닉 상태로, 일반적으로 이전 어텐션 블록 또는 정규화 모듈의 출력입니다. MoE 모듈의 핵심 메커니즘은 라우터를 사용하여 입력을 가장 관련 있는 전문가에게 할당하는 것입니다. 라우터는 일반적으로 학습 가능한 가중치 행렬 $`W_r^{(\ell)} \in \mathbb{R}^{d \times N}`$에 의해 매개변수화되며, Top-$`k`$ 소프트맥스 함수를 통해 전문가 할당(희소 게이팅 분포) $`a^{(\ell)}(x^{(\ell)}) \in \mathbb{R}^N`$을 생성합니다:

\begin{equation}
    a^{(\ell)}(x^{(\ell)}) = \mathrm{TopK}\left(\mathrm{Softmax}(x^{(\ell)} W_r^{(\ell)})\right).
\end{equation}

MoE 모듈의 최종 출력 $`h^{(\ell)}`$는 예측된 전문가 할당을 사용하여 선택된 전문가들의 출력의 선형 결합으로 계산됩니다:

\begin{equation}
    h^{(\ell)} = \sum_{i=1}^N a^{(\ell)}(x^{(\ell)})_i \cdot E^{(\ell)}_i(x^{(\ell)}).\nonumber
\end{equation}

표준 추론 중에 라우터 가중치 $`W_r^{(\ell)}`$은 고정되어 있습니다. 이 정적 라우팅 전략은 테스트 분포가 학습 분포에서 벗어날 때 적응성을 제한할 수 있습니다.

제안된 방법: kNN-MoE

우리는 kNN-MoE (그림 1)를 제안합니다. 이는 과거 라우터 입력 및 최적의 전문가 할당을 사용하는 메모리를 활용하여 라우팅 결정을 강화하는 검색 기반 프레임워크입니다. 우리는 각 MoE 모듈 $`\ell \in \mathcal{L}_{\text{MoE}}`$에 독립적인 메모리 저장소 $`\mathcal{M}^{(\ell)}`$를 장착합니다. 층 지수 $`(\ell)`$는 생략되며, 이 방법은 모든 층에서 동일하게 작동합니다. kNN-MoE에는 두 단계가 포함됩니다: (1) 메모리 구축 (§4.1), 이는 전문가 할당 메모리를 오프라인으로 생성하는 과정이며; (2) 신뢰성 기반 적응적 혼합 (§4.2), 추론 중에 저장된 전문가 할당을 검색하고 활용하는 과정입니다.

메모리 구축

메모리 구축의 목표는 층별 키-값 저장소 $`\mathcal{M} = \{(k_t, v_t)\}`$를 생성하는 것입니다. 여기서 키 $`k_t`$는 라우터 입력이고 값 $`v_t`$는 원래 라우터보다 우수한 최적의 전문가 할당입니다. 이 과정은 데이터 수집과 최적의 전문가 할당 도출 두 단계로 이루어집니다.

데이터 수집

우리는 참조 데이터셋 $`\mathcal{D}_{\text{ref}}`$를 사용합니다. 여기에는 정답 토큰 시퀀스가 포함되어 있습니다. $`\mathbf{y} = (y_1, \dots, y_T)`$는 $`\mathcal{D}_{\text{ref}}`$의 시퀀스를 나타냅니다. 우리는 이들 시퀀스에 대해 동결된 MoE 모델을 teacher-forcing 모드에서 실행합니다. 각 시간 단계 $`t \in [1,T]`$마다 현재 층의 라우터 입력 $`x_t`$와 해당 정답 토큰 $`y_t`$를 수집합니다. 이 라우터 입력은 검색 키로 사용되며, 즉 $`k_t = x_t`$입니다.

최적의 전문가 할당 도출

원래 라우팅 결정(방정식 [eq:router_gate]에서 정의된 것) 대신, 우리는 지상진실 토큰 $`y_t`$의 예측 확률을 최대화하는 최적의 전문가 할당을 저장합니다. 각 토큰에 대해 이는 최적화 문제로 표현됩니다.

$`\pi(r) = \mathrm{TopK}(\mathrm{Softmax}(r))`$은 로짓 $`r \in \mathbb{R}^N`$에서 희소 전문가 가중치로 매핑하는 것을 나타냅니다. 특정 토큰 $`t`$에 대해, 우리는 학습 가능한 로짓 벡터 $`r_t`$를 도입하여 파라미트릭 출력 $`x_t W_r`$을 대체합니다. 우리는 $`r_t`$를 최적화하여 목표 토큰 $`y_t`$의 음의 로그 가능성을 최소화합니다:

\begin{align}
    r_t^{*} &= \mathop{\rm arg~min}\limits_{r \in \mathbb{R}^N} \mathcal{L}_t(r), \\
    \mathcal{L}_t(r) &= - \log p_\theta(y_t \mid x_t, \text{routing}=\pi(r)), \nonumber
\end{align}

여기서 $`\theta`$는 네트워크의 나머지 동결된 파라미터를 나타냅니다.

우리는 방정식 [eq:gold_routing_obj]을 경사 하강법을 통해 해결합니다. 우리는 $`r_t`$를 원래 파라미트릭 로짓으로 초기화합니다, 즉 $`r_t^{(0)} = x_t W_r`$. 그런 다음 $`S`$ 단계의 업데이트를 수행합니다:

\begin{equation}
    r_t^{(s+1)} = r_t^{(s)} - \eta \nabla_r \mathcal{L}_t(r_t^{(s)}), ~~ s = 0, \dots, S-1,\nonumber
\end{equation}

여기서 $`\eta`$는 학습률입니다. $`r_t`$를 일반 층에 대해 설명하지만 이 최적화는 모델 전체에서 동시에 수행됩니다; 구체적으로, 모든 MoE 층의 라우팅 로짓 $`\{r_t^{(\ell)}\}_{\ell \in \mathcal{L}_{\text{MoE}}}`$은 손실을 최소화하기 위해 동시에 업데이트됩니다. 또한, 최적화 및 데이터 수집 과정은 $`\mathcal{D}_{\text{ref}}`$의 서로 다른 시퀀스 간에 독립적으로 수행됩니다.

최종 최적화된 할당은 $`a^*(x_t) = \pi(r_t^{(S)})`$. 이 값이 메모리에서의 타겟 값, 즉 $`v_t = a^*(x_t)`$를 나타냅니다. 이것은 “최적” 선택을 나타냅니다: 다음 토큰을 가장 잘 예측하기 위해 어떤 전문가들이 선택되어야 하는지를 나타냅니다.

마지막으로 현재 층의 메모리는 다음과 같이 구축됩니다:

\begin{equation}
    \mathcal{M} = \{(x_t, a^*(x_t)) \mid t \in \mathcal{D}_{\text{ref}}\}.\nonumber
\end{equation}

이 과정은 $`\mathcal{L}_{\text{MoE}}`$의 모든 층에 대해 반복됩니다.

신뢰성 기반 적응적 혼합

추론 중에는 각 MoE 레이어와 각 라우터 입력 $`x`$에 대해 해당 메모리에서 가장 가까운 이웃 집합 $`\mathcal{N}(x) \subset \mathcal{M}`$을 검색합니다.

비파라미트릭 전문가 할당 제안 $`a_{\text{mem}}(x)`$는 입력과의 유사도에 따라 검색된 전문가 할당을 집계하여 정의됩니다. 구체적으로, $`\{(k_j, v_j)\}_{j=1}^K`$가 $`\mathcal{N}(x)`$에서 검색된 키-값 쌍이라고 가정합니다. 메모리 기반 전문가 할당은 다음과 같이 계산됩니다:

\begin{equation}
    a_{\text{mem}}(x) = \sum_{j=1}^K \frac{s(x, k_j)}{\sum_{m=1}^K s(x, k_m)} \, v_j,\nonumber
\end{equation}

여기서 $`s(\cdot, \cdot)`$는 유사도 함수입니다.

파라미트릭 라우터 출력 $`a(x)`$(방정식 [eq:router_gate]에서 정의된 것)와 비파라미트릭 제안 $`a_{\text{mem}}(x)`$을 결합하기 위해, 우리는 검색 신뢰도를 반영하는 적응적 혼합 계수 $`\lambda(x)`$를 도입합니다. 이 신뢰도는 이웃의 평균 유사성을 통해 측정됩니다:

\begin{equation}
    \lambda(x) = \frac{1}{K} \sum_{j=1}^K s(x, k_j).\nonumber
\end{equation}

최종 전문가 할당은 파라미트릭 및 메모리 기반 할당 사이의 선형 보간을 통해 얻어집니다:

\begin{equation}
    a_{\text{final}}(x) = (1 - \lambda(x)) a(x) + \lambda(x) a_{\text{mem}}(x).\nonumber
\end{equation}

마지막으로, 우리는 $`a_{\text{final}}(x)`$를 사용하여 MoE 레이어 출력 $`h`$를 계산합니다:

\begin{equation}
    h = \sum_{i=1}^N a_{\text{final}}(x)_i \cdot E_i(x).\nonumber
\end{equation}

이 혼합은 $`\lambda(x) \approx 1`$일 때 모델이 검색된 할당에 신뢰하고 라우터를 수정하며, 반면에 $`\lambda(x) \approx 0`$일 때는 파라미트릭 라우터로 돌아가서 검색 노이즈를 피합니다.

실험

실험 설정

ArXiv 원문 PDF 보기

📊 논문 시각자료 (Figures)

감사의 말씀

이 글의 저작권은 연구하신 과학자분들께 있으며, 인류 문명 발전에 공헌해주신 노고에 감사를 드립니다.

관련 게시글

3D 다중 객체 장면에서의 2D 시스템 비디오와 언어 정합성 및 멀티정보 도함수 없는 제어

AI 강화된 양자점 해밀토니안 튜닝을 통한 마이저나 모드 형성

AI 기반 다중 클러스터 환경의 클라우드 리소스 최적화

검색 시작

검색어를 입력하세요

검색 중...

검색 결과 없음

다른 검색어로 시도해보세요

↑↓ 이동

↵ 선택

ESC 닫기

⌘K 단축키

목차

点击标题快速跳转

목차

제목을 클릭하면 해당 위치로 이동합니다

모델	방법	GPQA	MMLU	SuperGPQA	USMLE	MedMCQA
OLMoE	Zero-shot	27.27	46.77	13.02	32.81	35.57
	5-shot	21.72	33.06	11.09	31.31	25.36
	SFT	21.72	46.89	13.67	37.84	34.78
	SFT (Router Only)	24.24	45.27	11.66	31.22	34.23
	kNN-MoE (Ours)	29.80	47.81