길이 인식 적대적 학습을 통한 가변 길이 궤적 생성 몰 쇼핑객 경로를 위한 디지털 트윈
📝 원문 정보
- Title: Length-Aware Adversarial Training for Variable-Length Trajectories: Digital Twins for Mall Shopper Paths
- ArXiv ID: 2601.01663
- 발행일: 2026-01-04
- 저자: He Sun, Jiwoong Shin, Ravi Dhar
📝 초록 (Abstract)
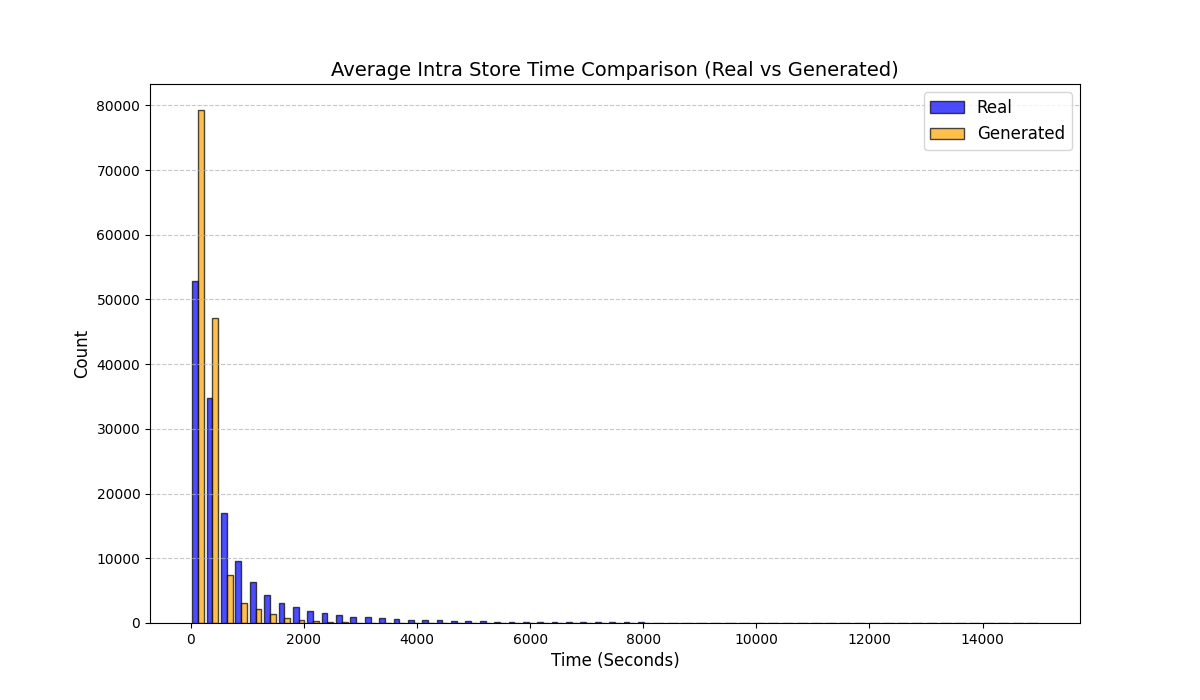
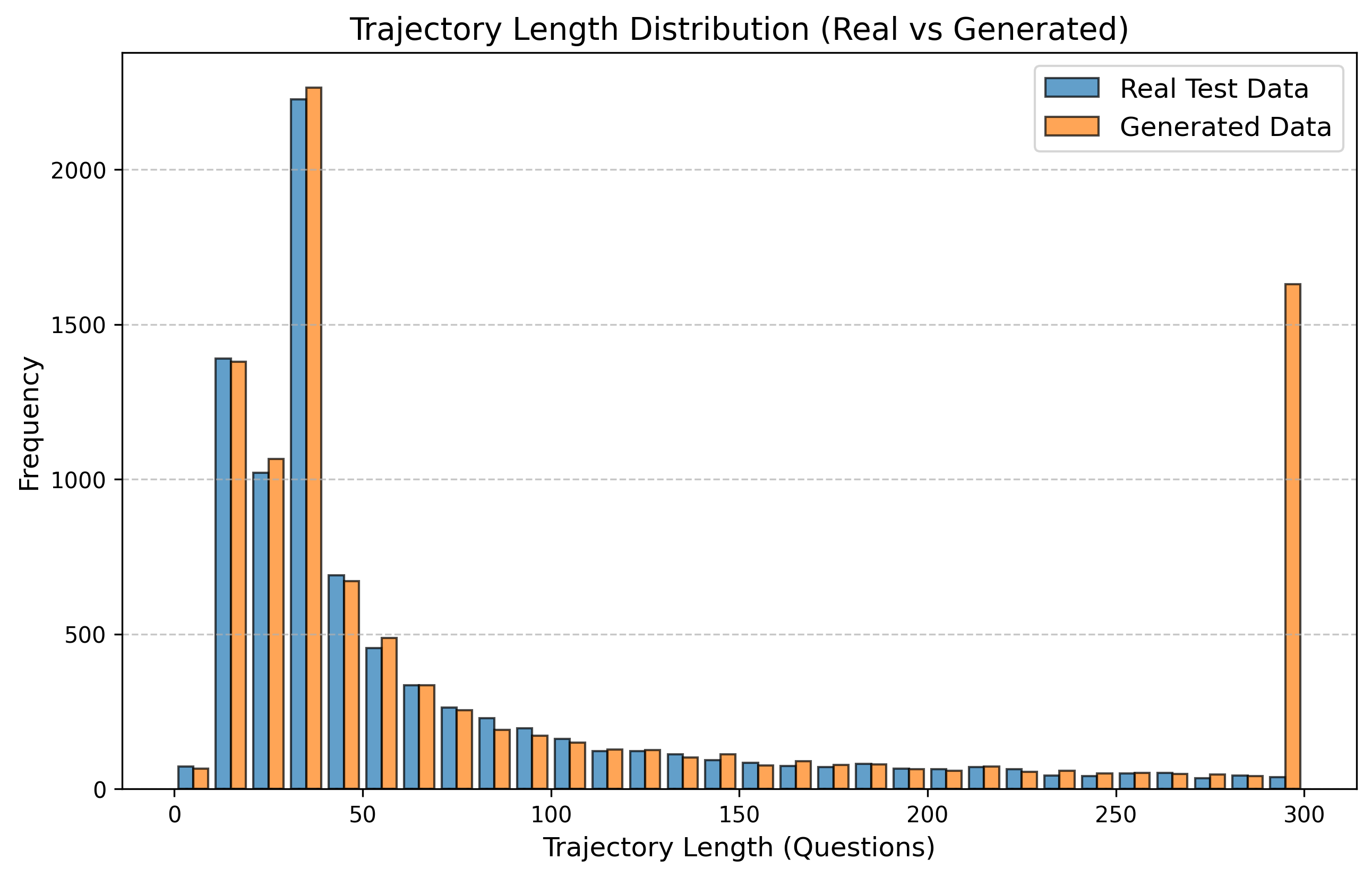
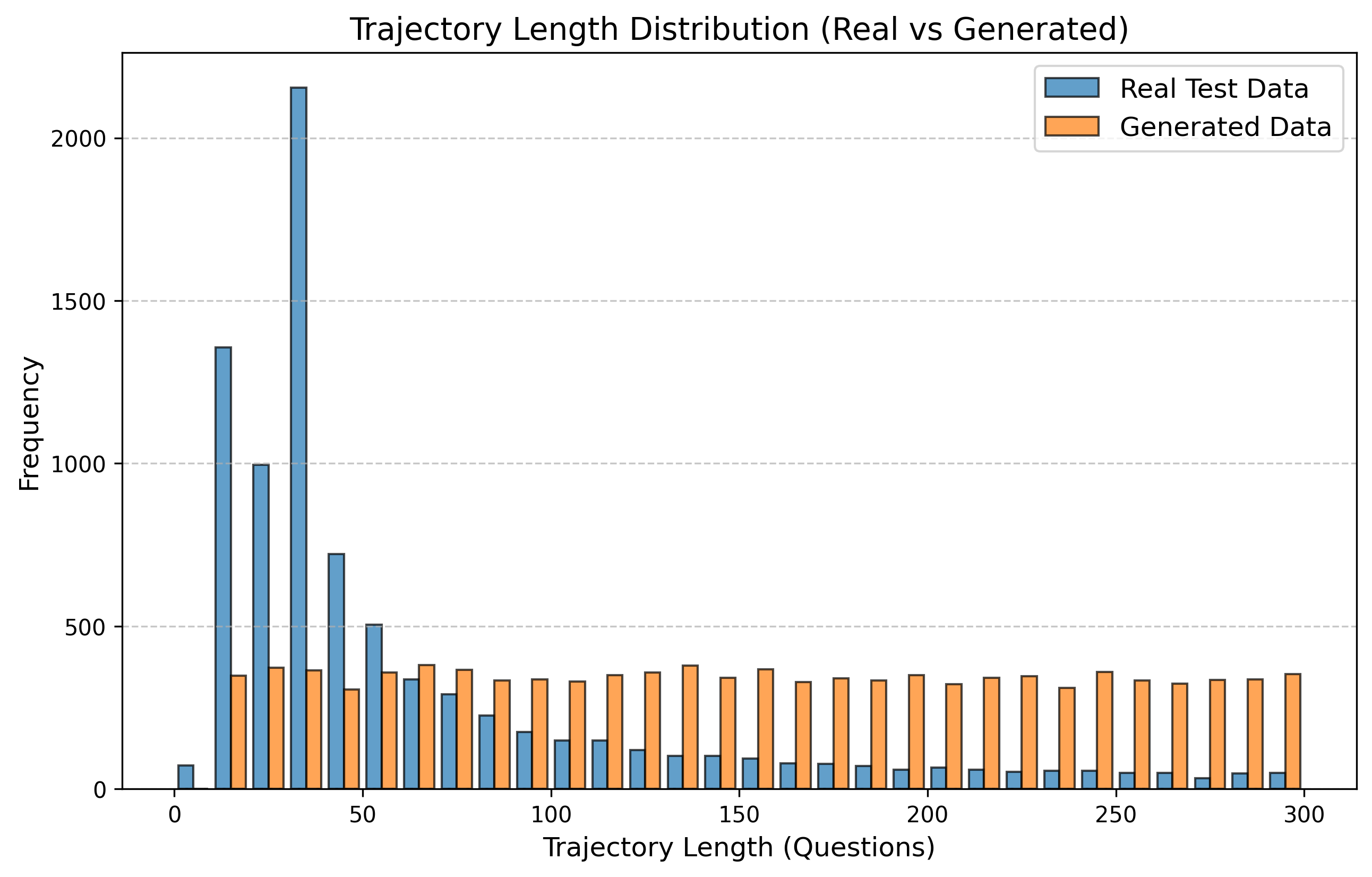
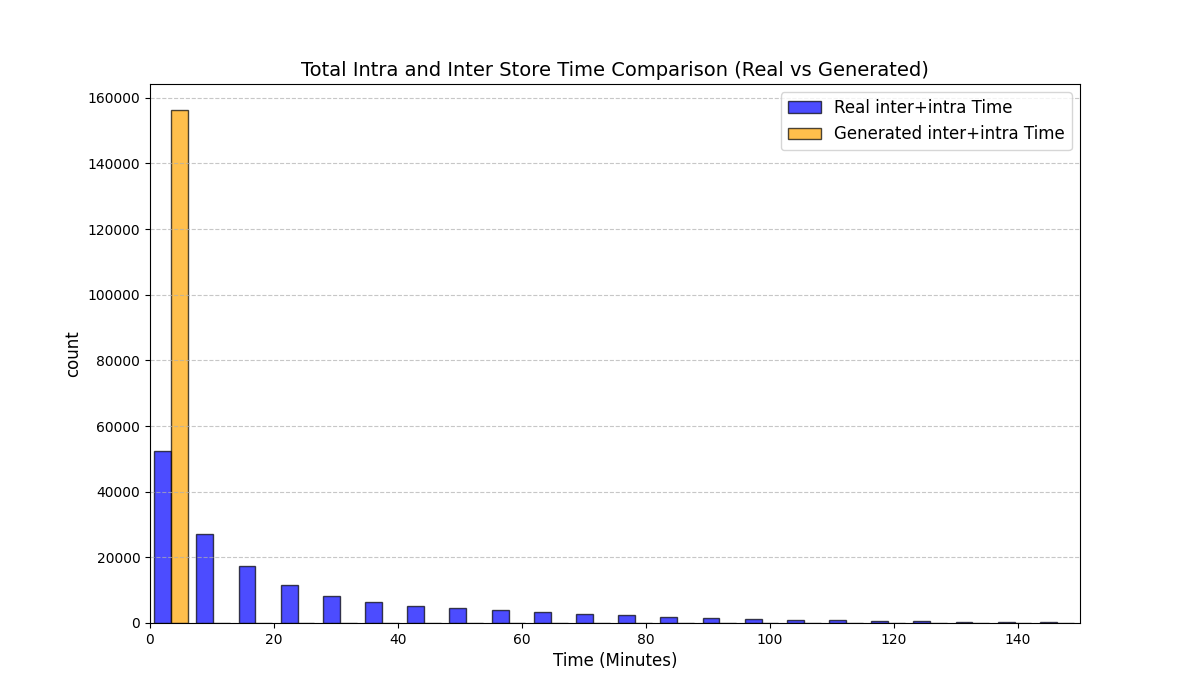
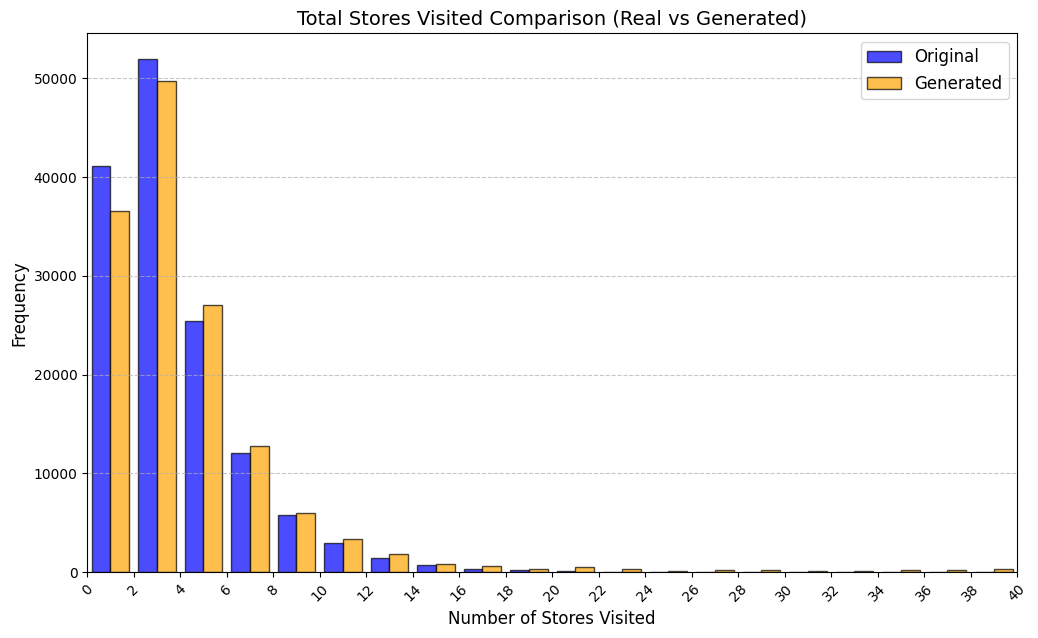
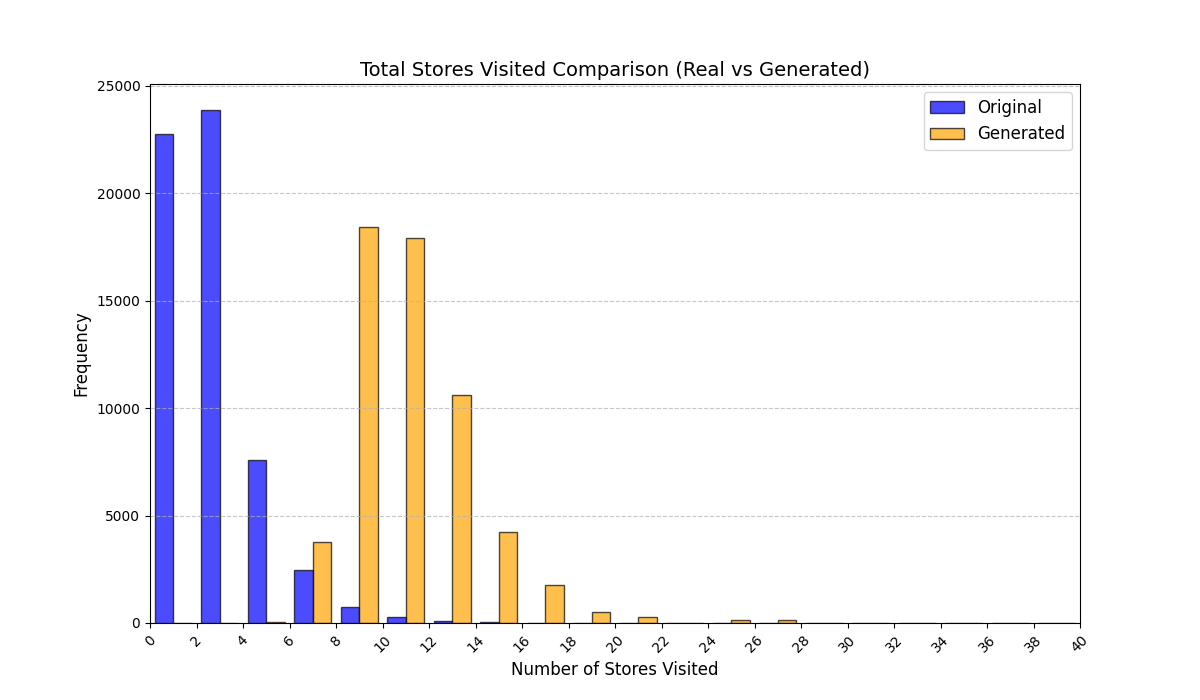
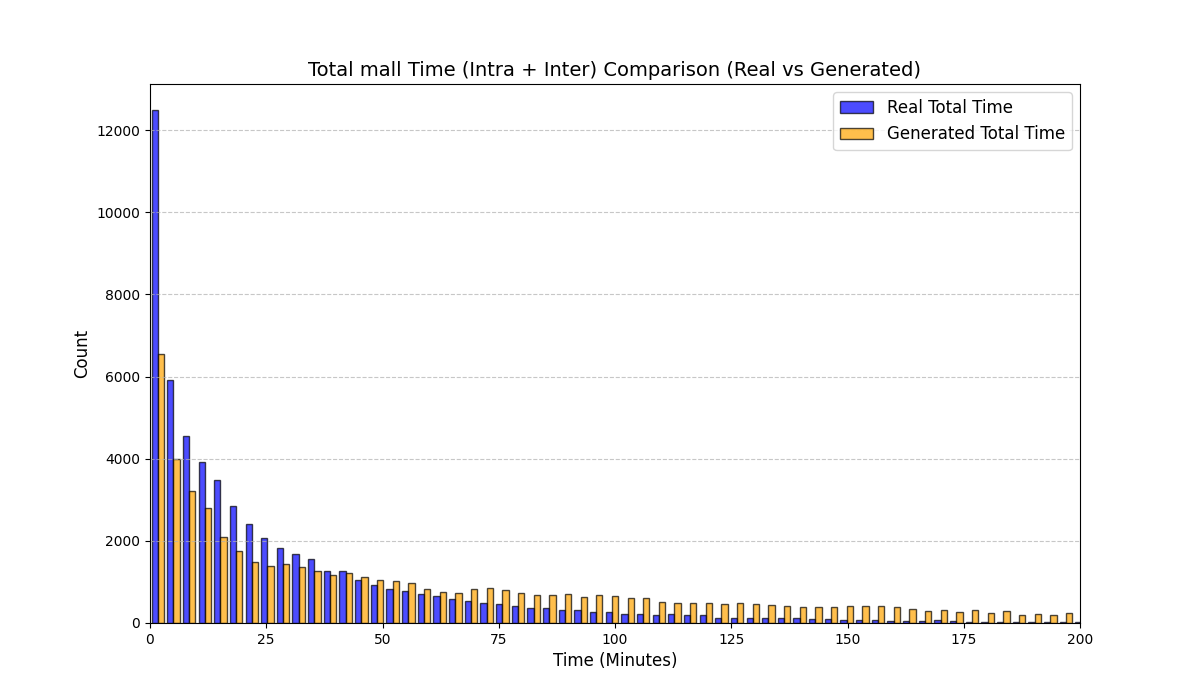
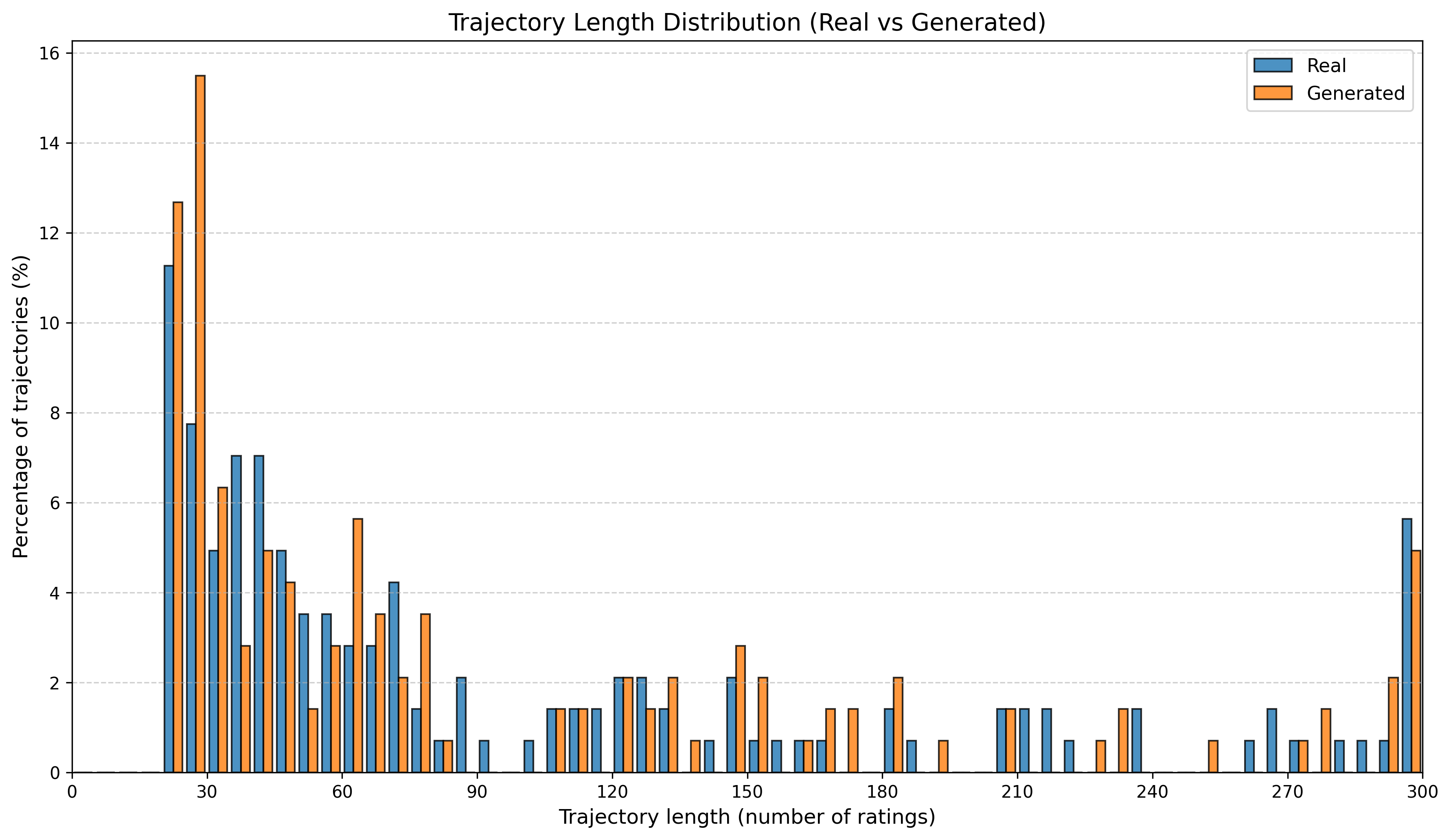
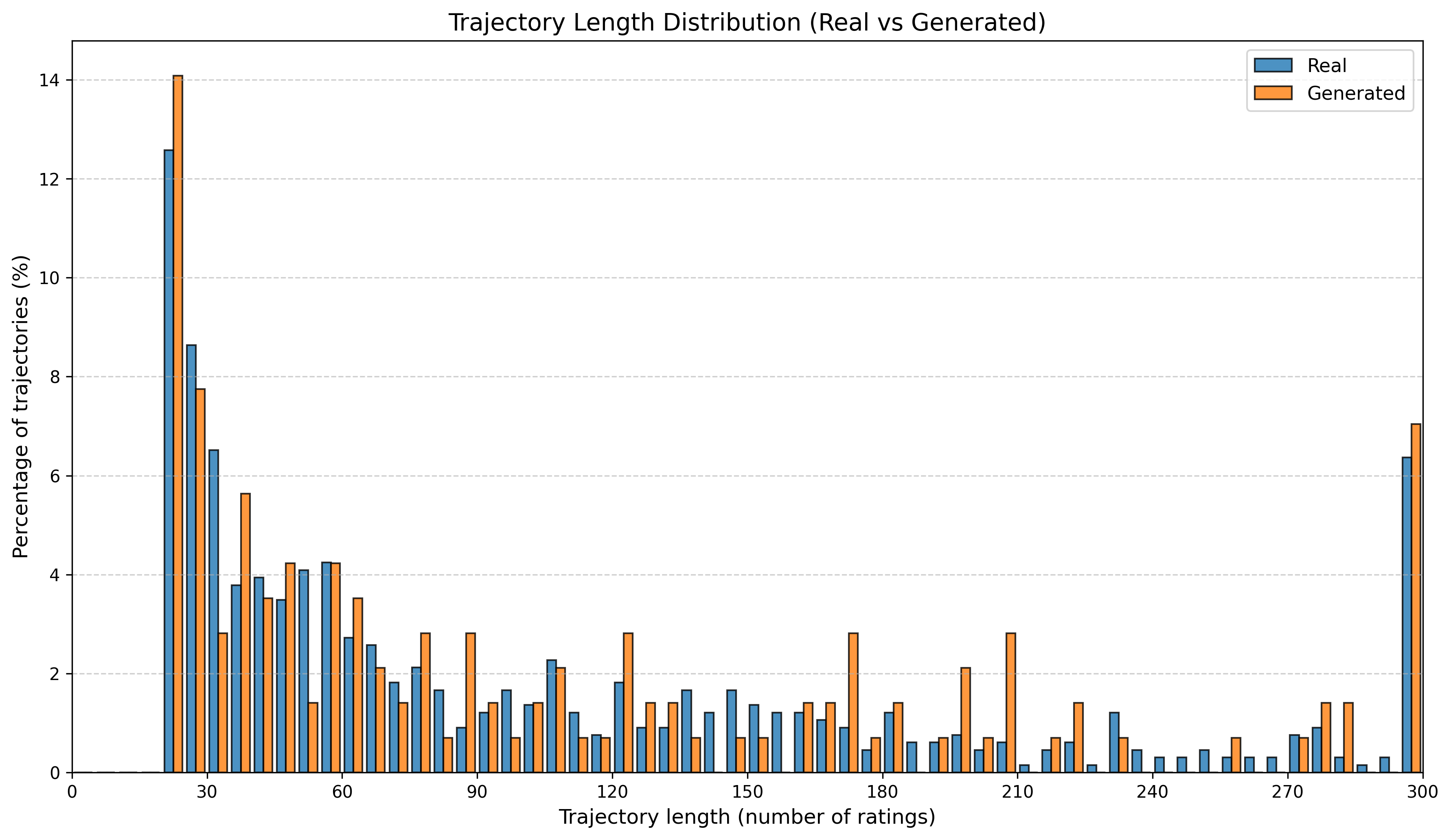
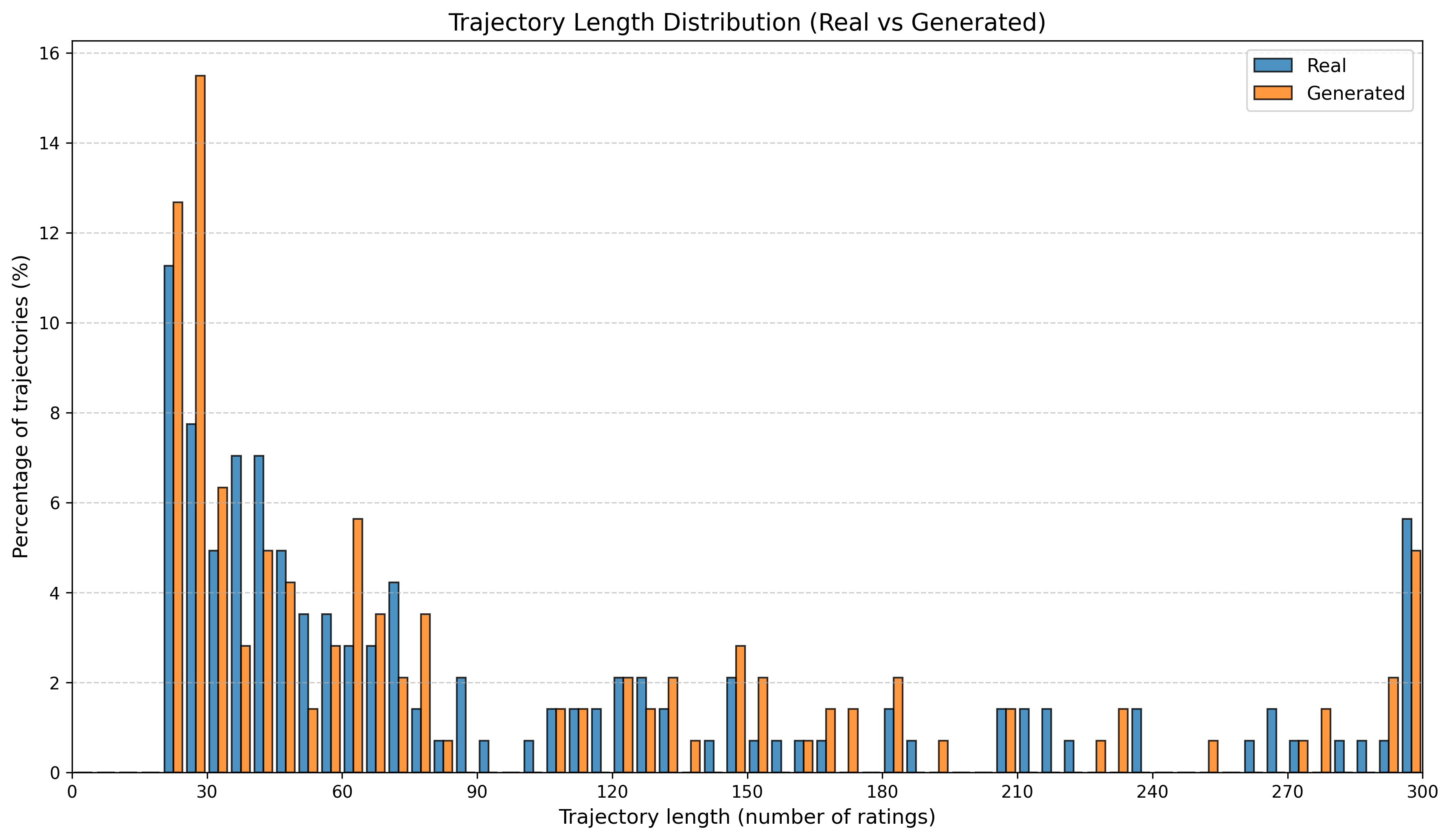
우리는 방문한 위치·아이템과 타임스탬프가 포함된 가변 길이 궤적(시퀀스)의 생성 모델링을 연구한다. 배치 학습 시 궤적 길이의 이질성이 클 경우 학습이 불안정해지고, 이는 궤적 기반 통계량의 분포 매칭을 저하시킨다. 이를 해결하기 위해 길이‑인식 샘플링(LAS)이라는 간단한 배치 전략을 제안한다. LAS는 궤적을 길이별 버킷으로 묶고, 동일 버킷에서만 배치를 샘플링함으로써 배치 내 길이 이질성을 감소시킨다. 모델 클래스는 변형하지 않으며, 조건부 트래젝터리 GAN에 LAS와 시간 정렬 보조 손실을 통합한다. 우리는 (i) 완만한 유계 가정 하에 파생 변수에 대한 분포 수준 보장을, (ii) 길이 전용 단축 크리틱을 제거하고 버킷 내 차이를 목표로 하는 IPM/워셔스테인 메커니즘을 제시한다. 실험 결과, LAS는 다중 몰 쇼핑객 궤적 데이터와 GPS·교육·전자상거래·영화 등 다양한 공개 시퀀스 데이터셋에서 파생 변수 분포 매칭을 일관되게 개선하고, 데이터셋별 지표에서 무작위 샘플링을 능가한다.💡 논문 핵심 해설 (Deep Analysis)
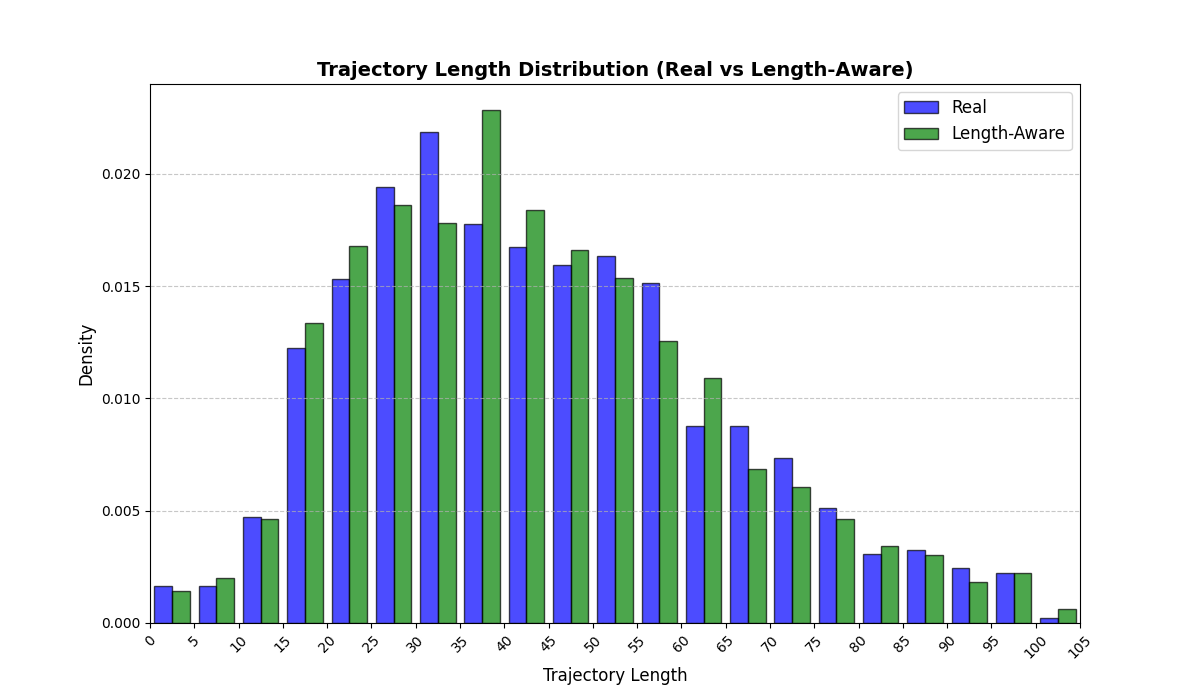
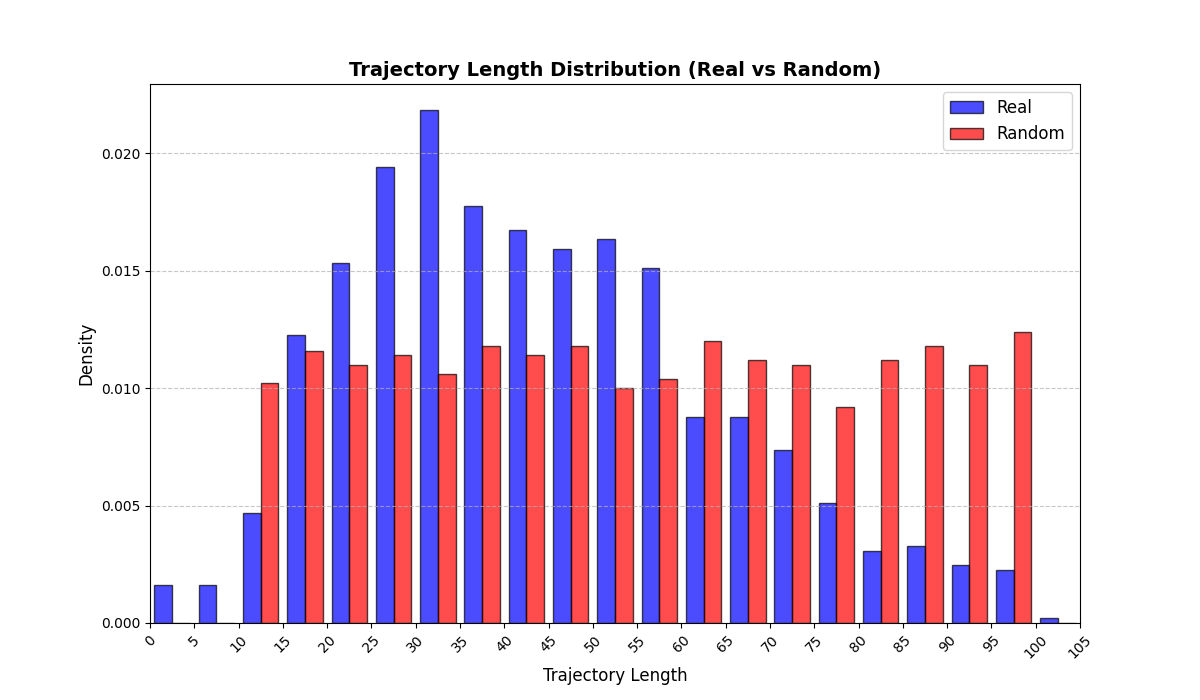
길이‑인식 샘플링(LAS)은 이러한 문제를 근본적으로 해결한다. 먼저 전체 데이터셋을 길이별 버킷으로 나누고, 각 버킷 내부에서만 배치를 구성한다. 이렇게 하면 배치 내 길이 이질성이 최소화되어 그래디언트의 분산이 감소하고, 학습이 보다 안정적으로 진행된다. 또한 판별자는 길이 정보를 활용할 여지가 사라지므로, “길이 전용 단축 크리틱”이 사라진다. 논문은 이를 IPM(Integral Probability Metric) 및 Wasserstein 거리 관점에서 정량화한다. 즉, 길이 버킷 내에서의 분포 차이를 직접 최소화함으로써 전체 분포 매칭이 자연스럽게 향상된다는 메커니즘을 제시한다.
이론적 기여로는 두 가지가 있다. 첫째, 파생 변수에 대해 “분포‑수준 보장(distribution‑level guarantee)”을 제공한다. 이는 각 파생 변수가 유계(bounded)라는 가정 하에, LAS를 적용한 경우 실제 데이터와 생성 데이터 간의 차이가 ε 이하로 수렴한다는 형태의 수학적 결과다. 둘째, 길이‑전용 단축 크리틱을 제거함으로써 판별자가 학습해야 할 목표가 “버킷 내부의 미세한 차이”로 전환된다는 IPM/Wasserstein 메커니즘을 제시한다. 이는 기존 무작위 샘플링이 배치 내 길이 차이 때문에 판별자 손실이 크게 변동하고, 결국 생성기가 불필요한 길이 정보를 학습하게 되는 현상을 이론적으로 설명한다.
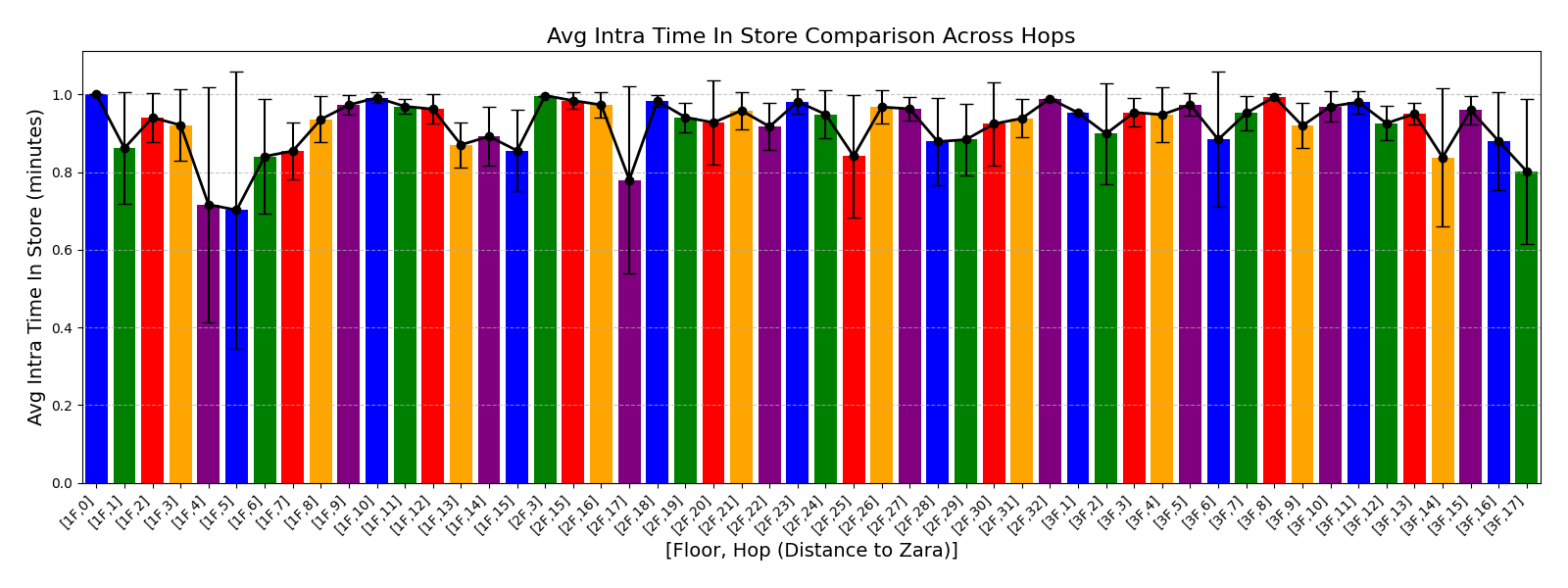
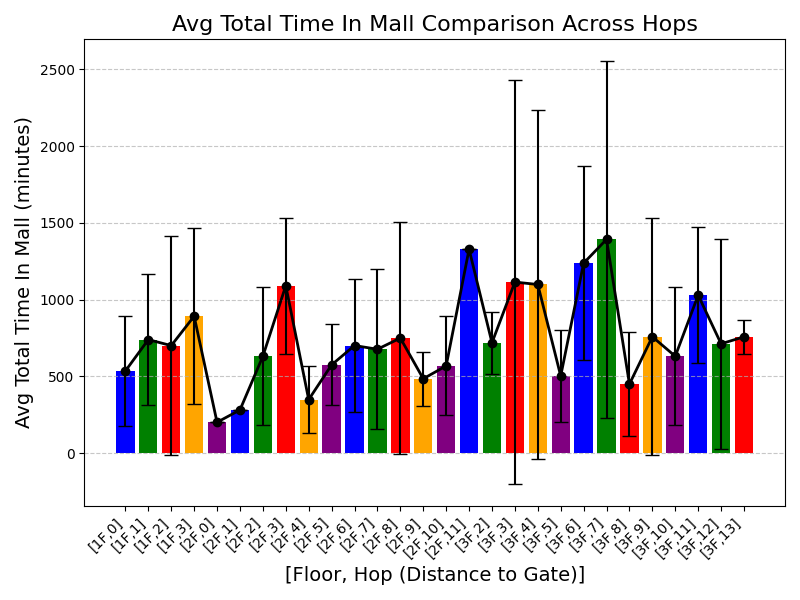
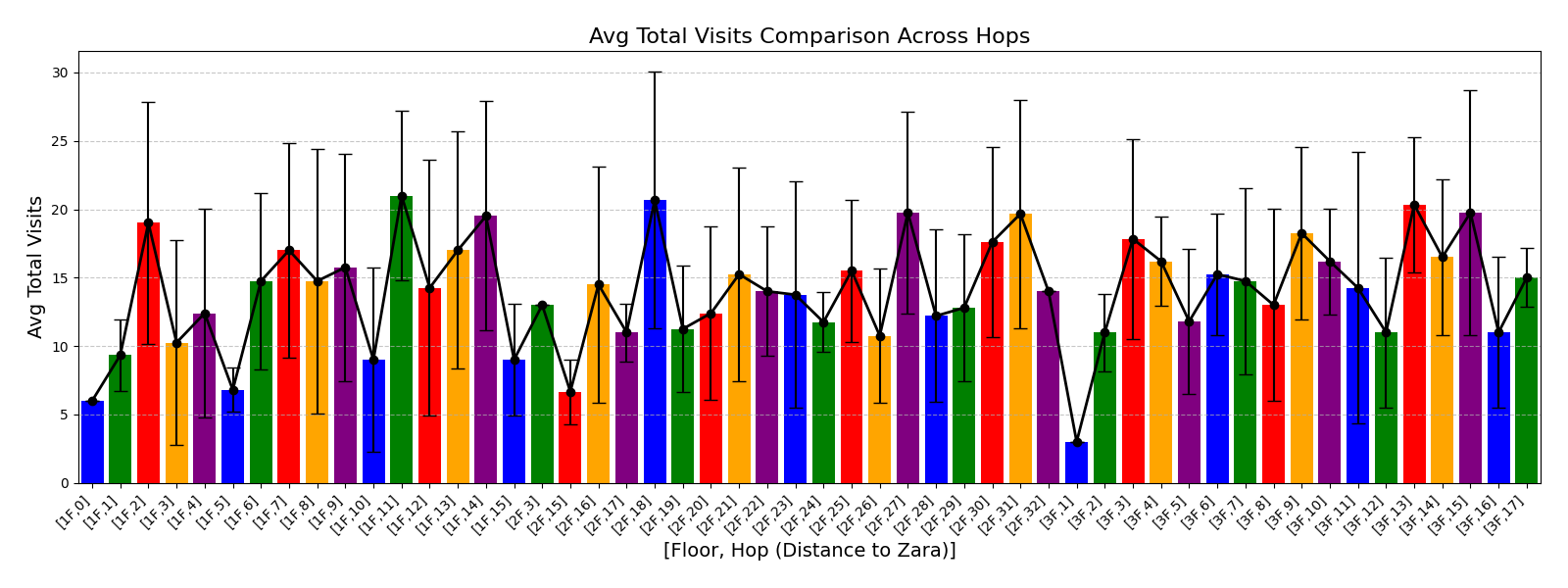
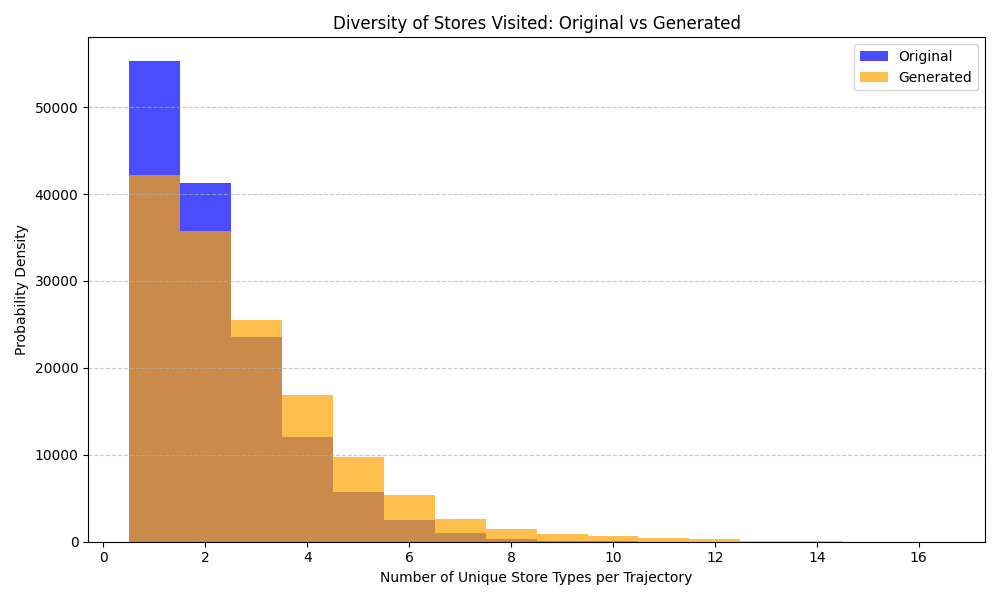
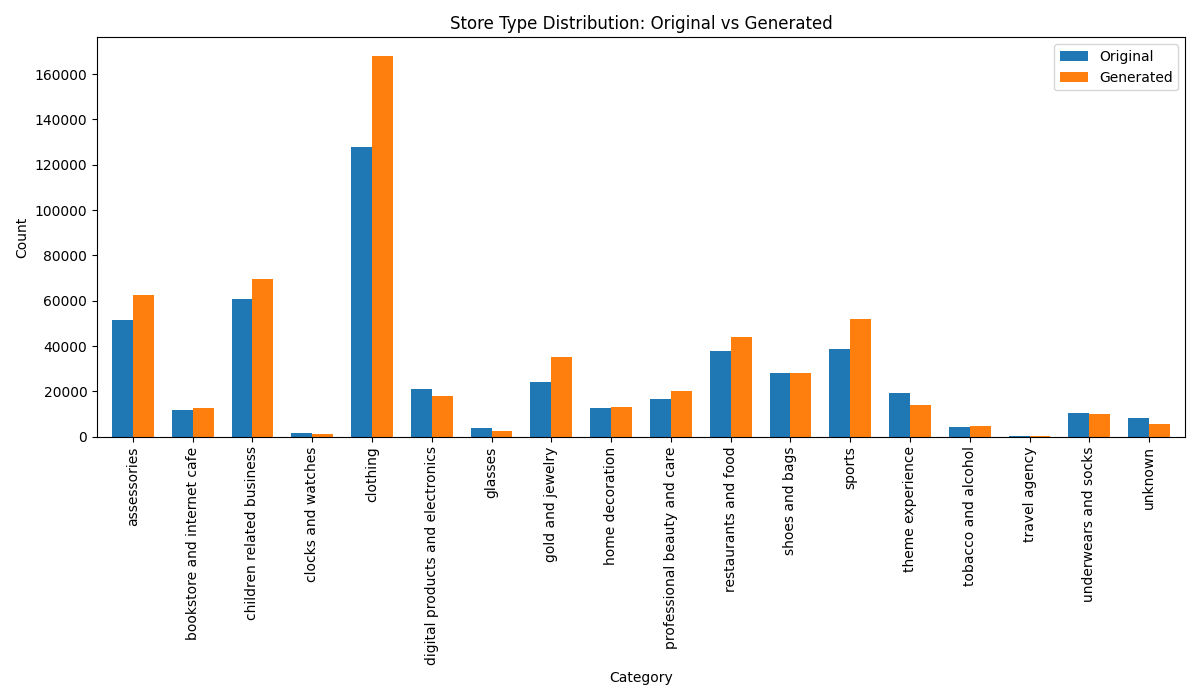
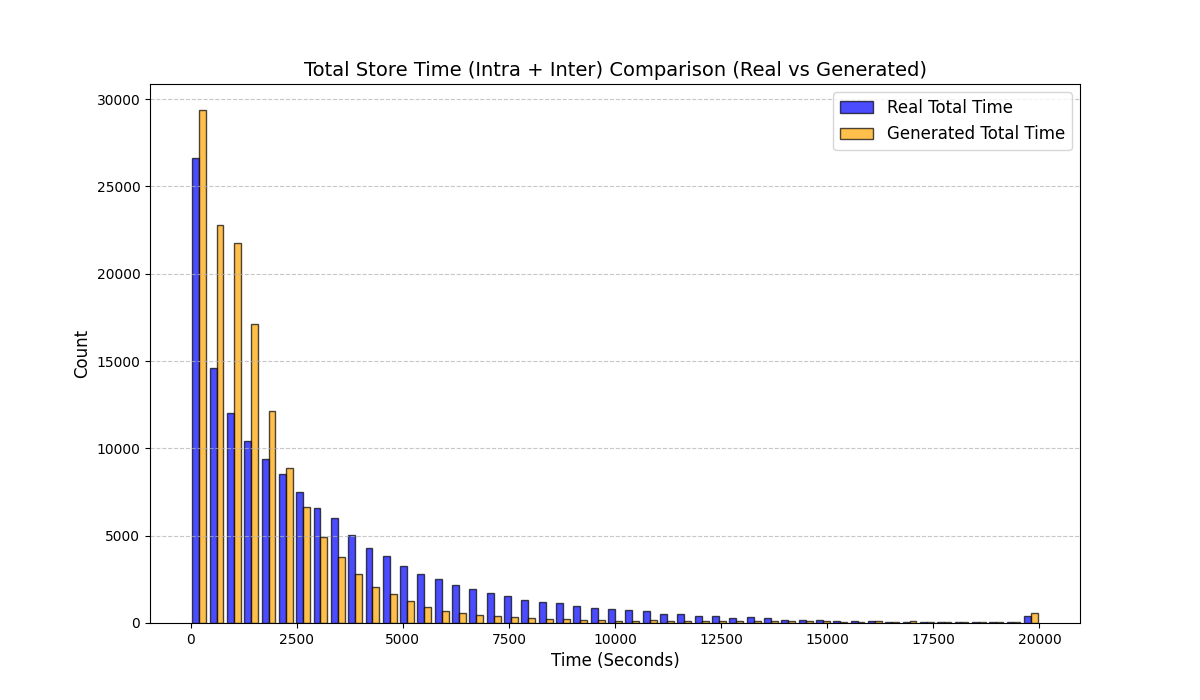
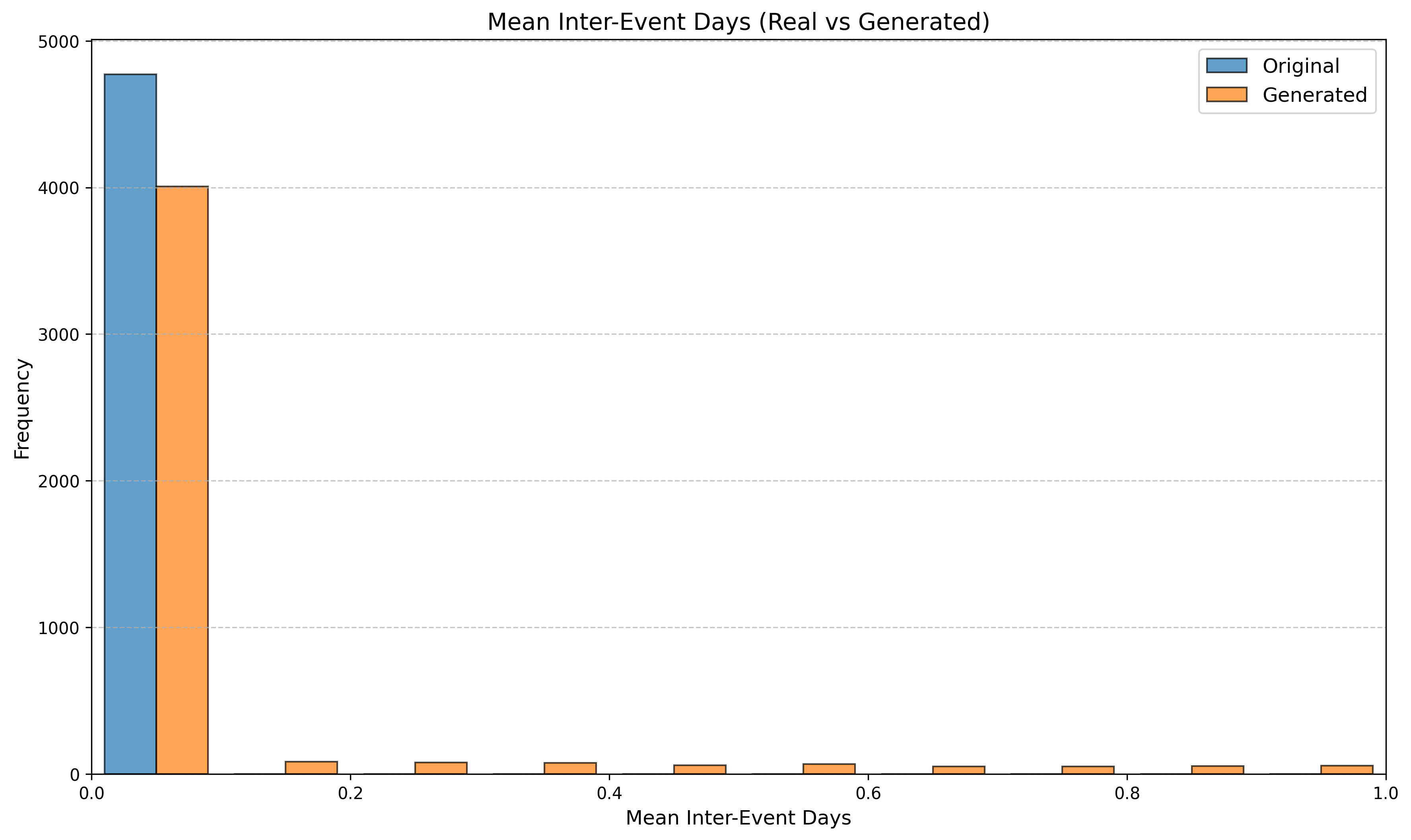
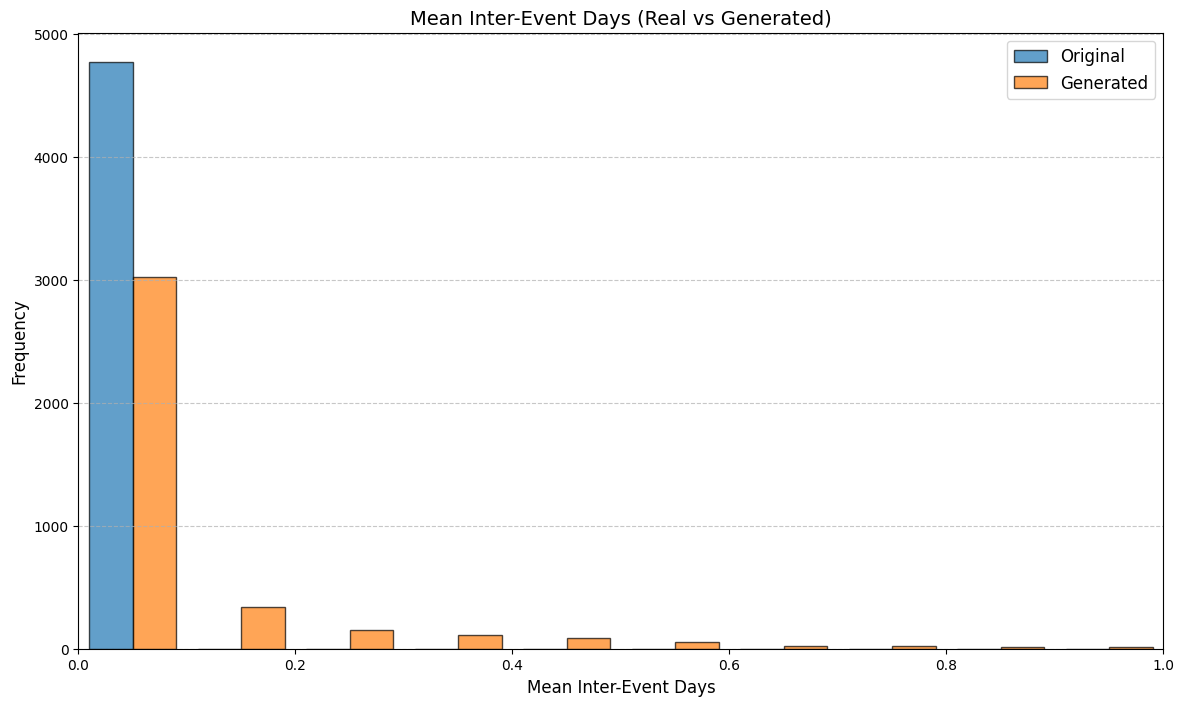
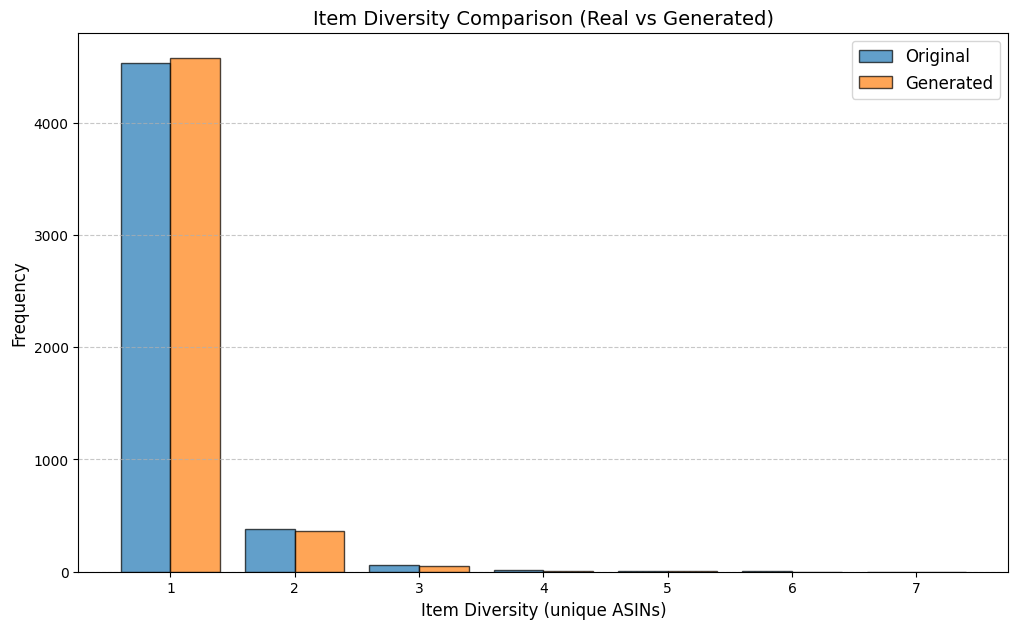
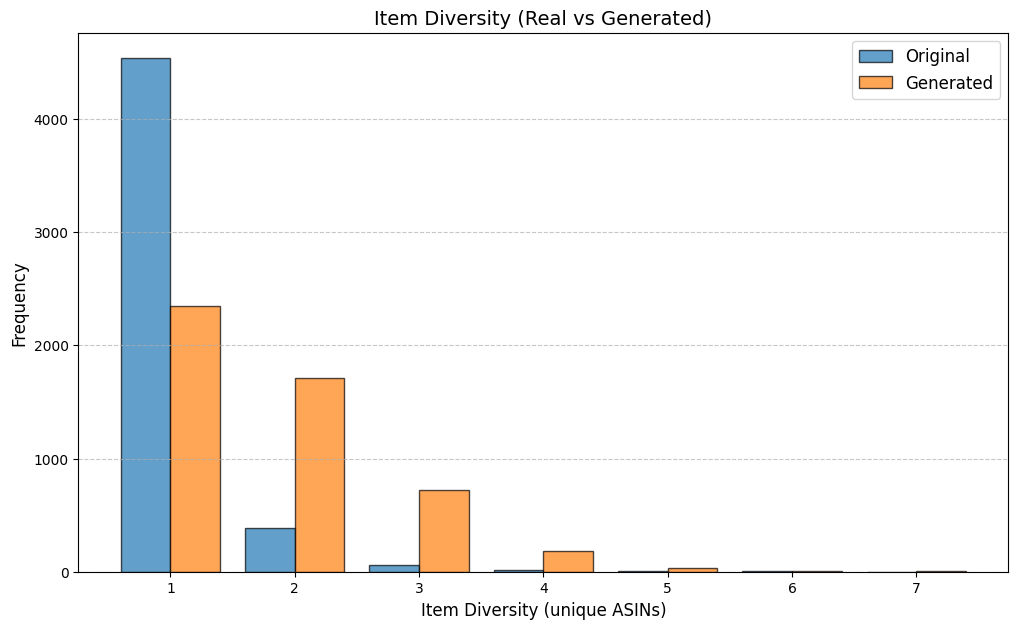
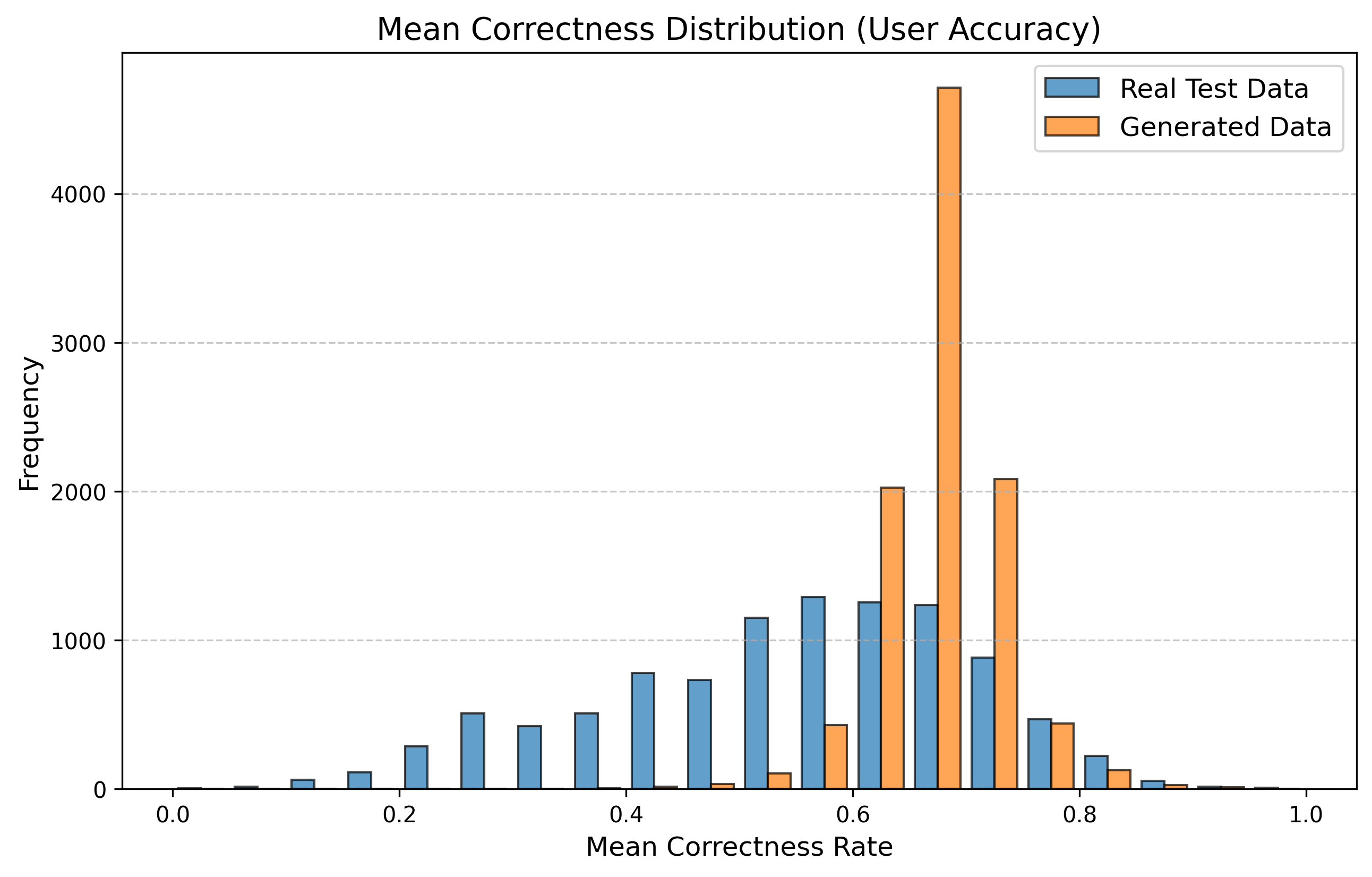
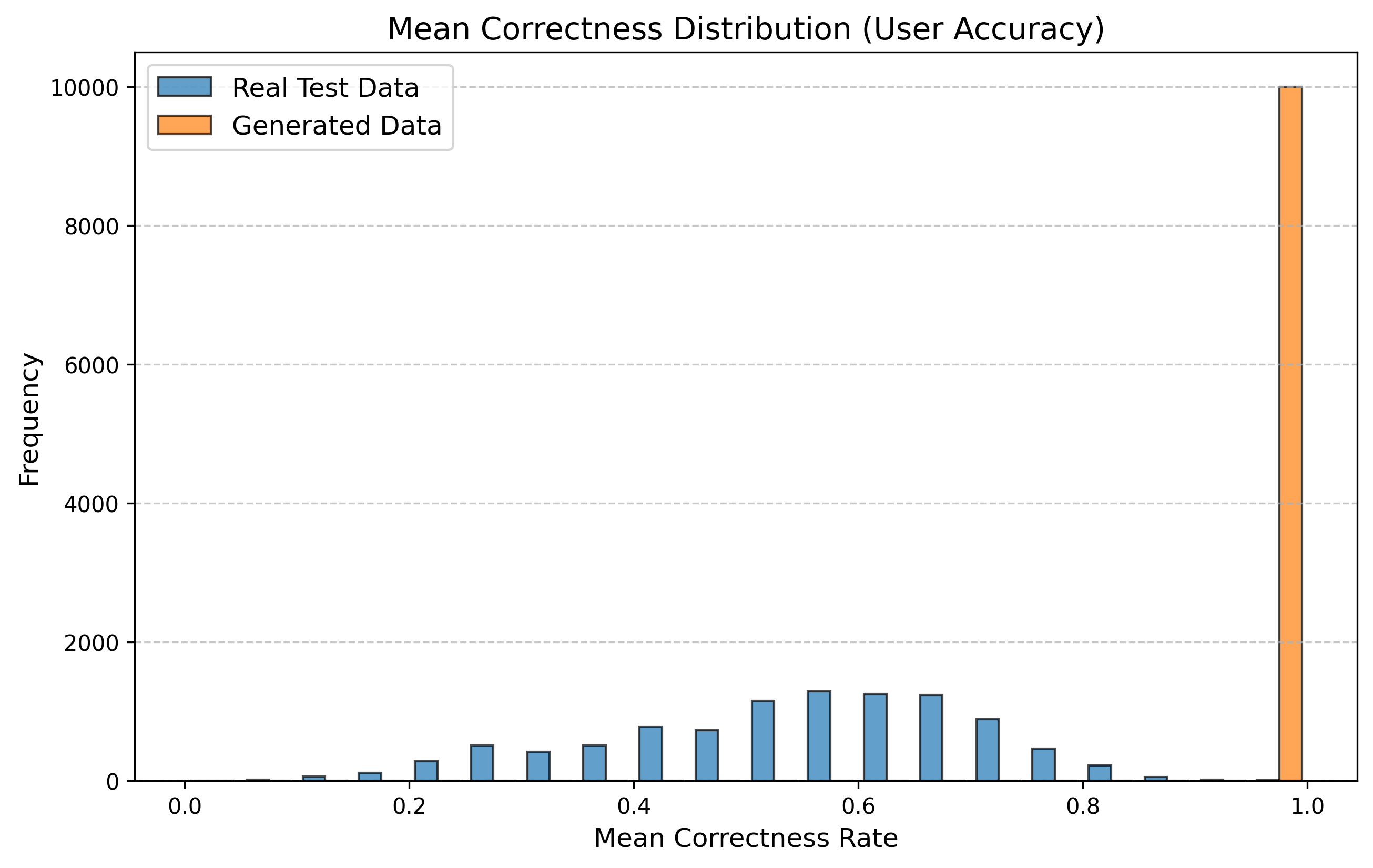
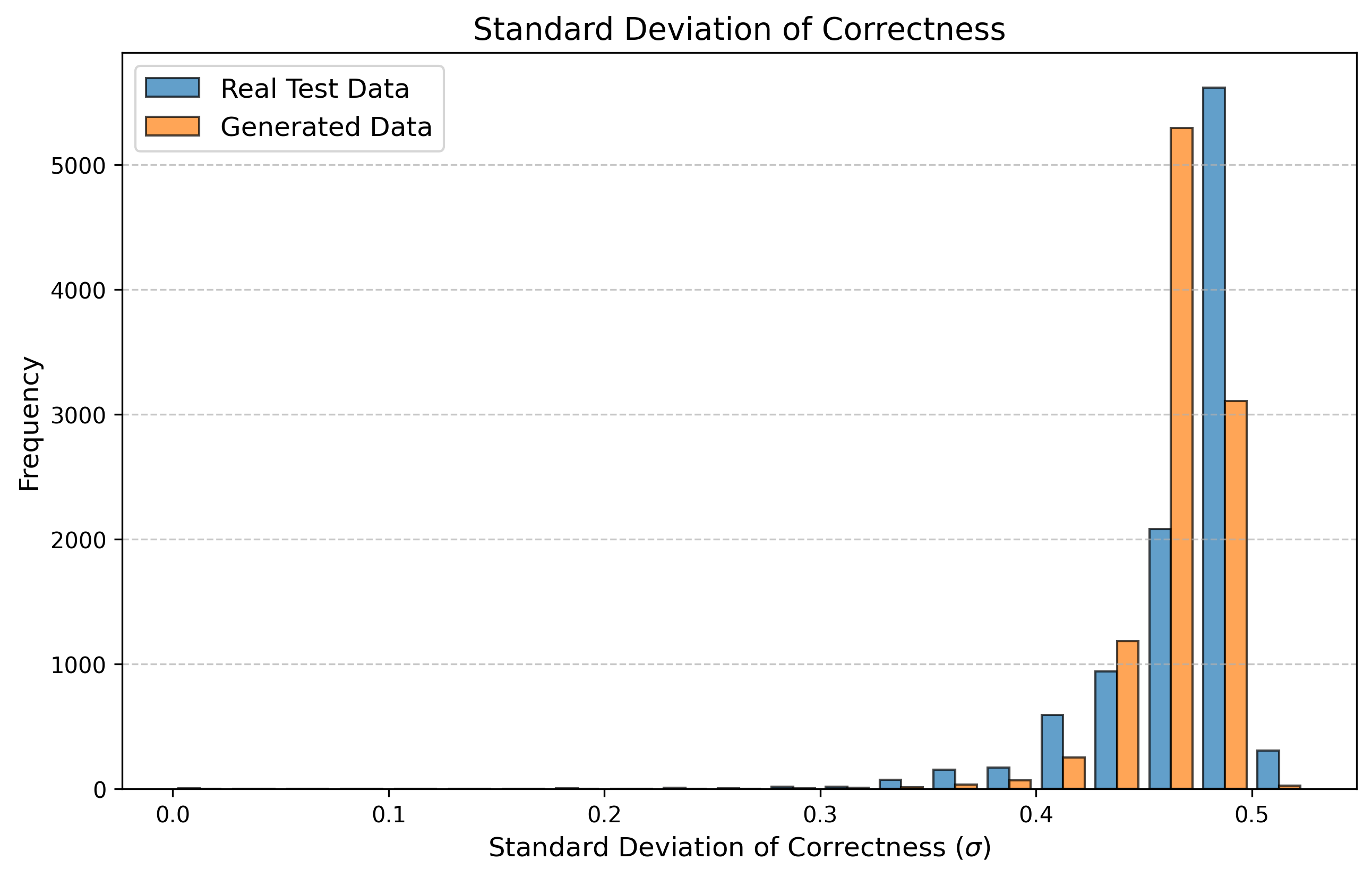
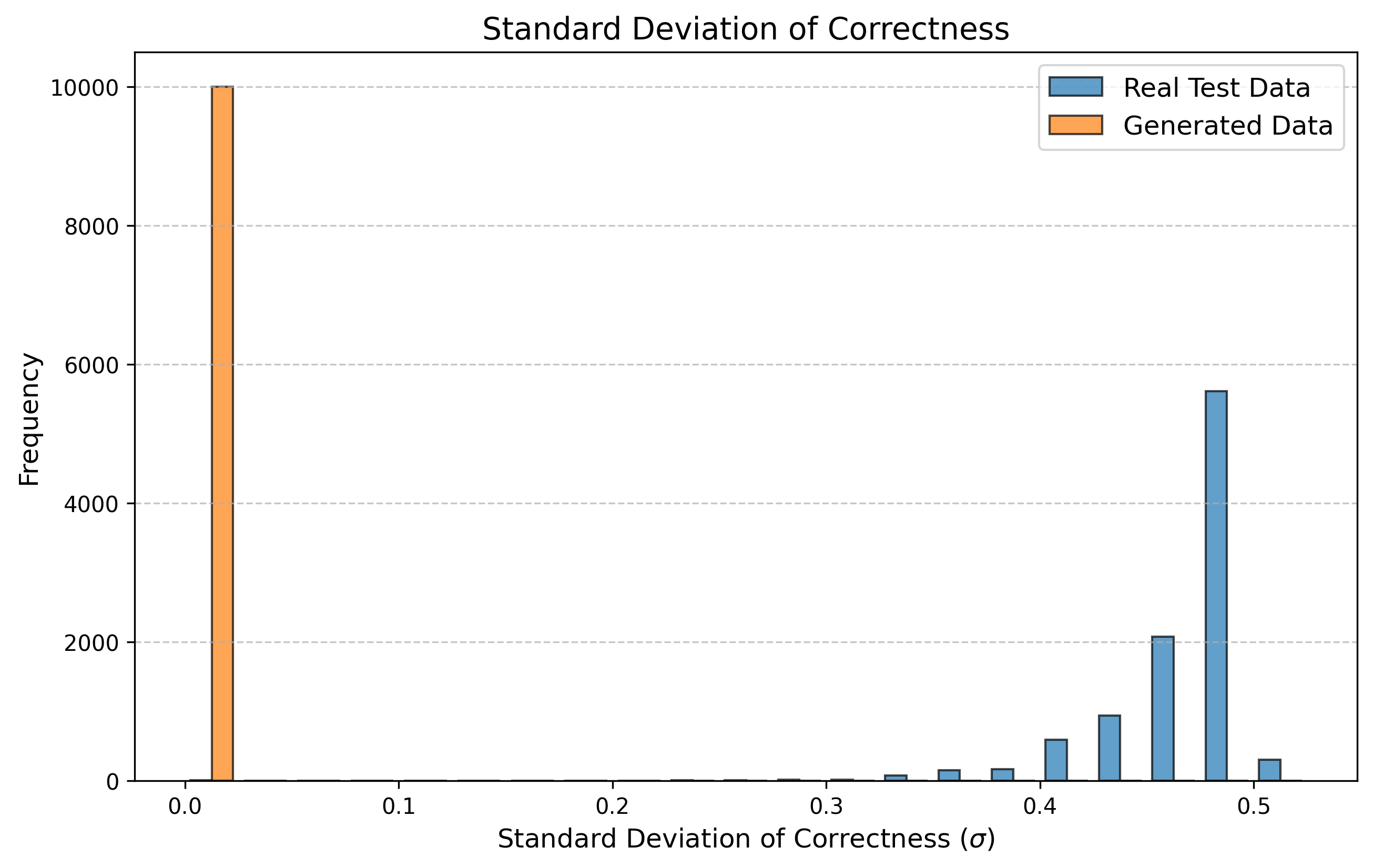
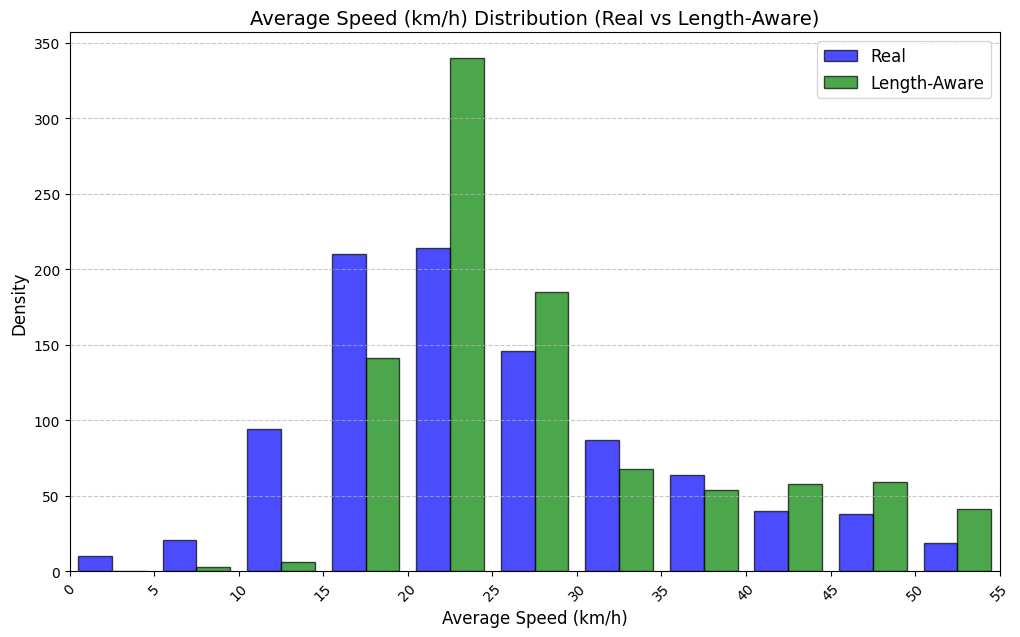
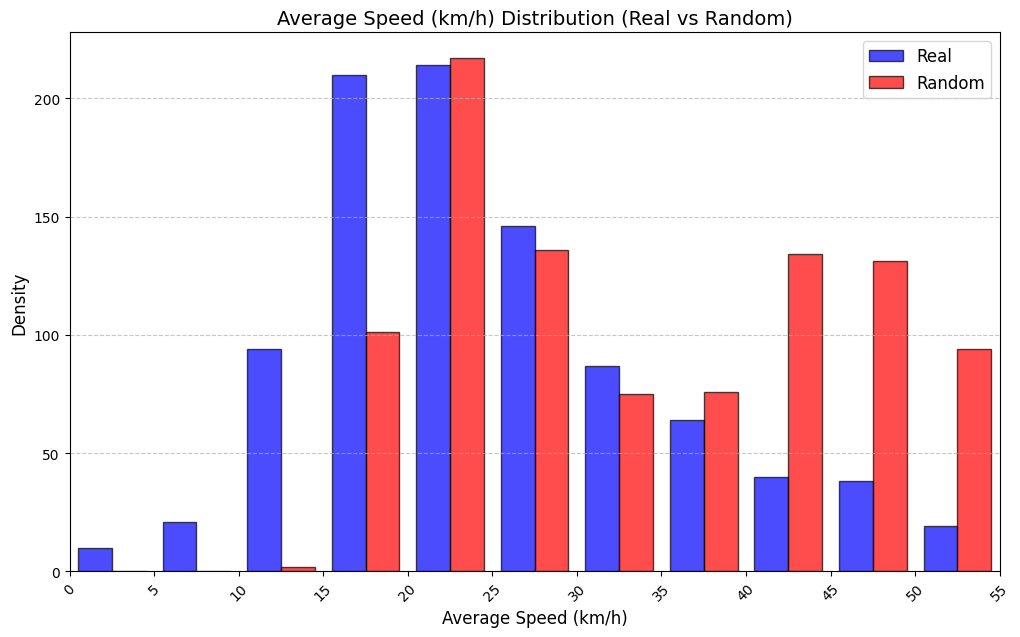
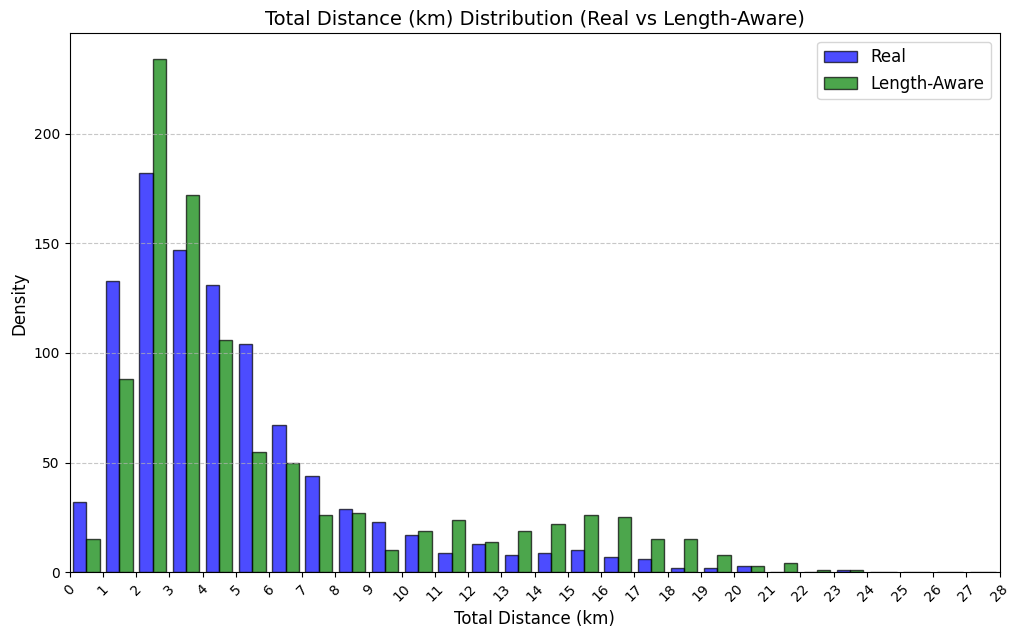
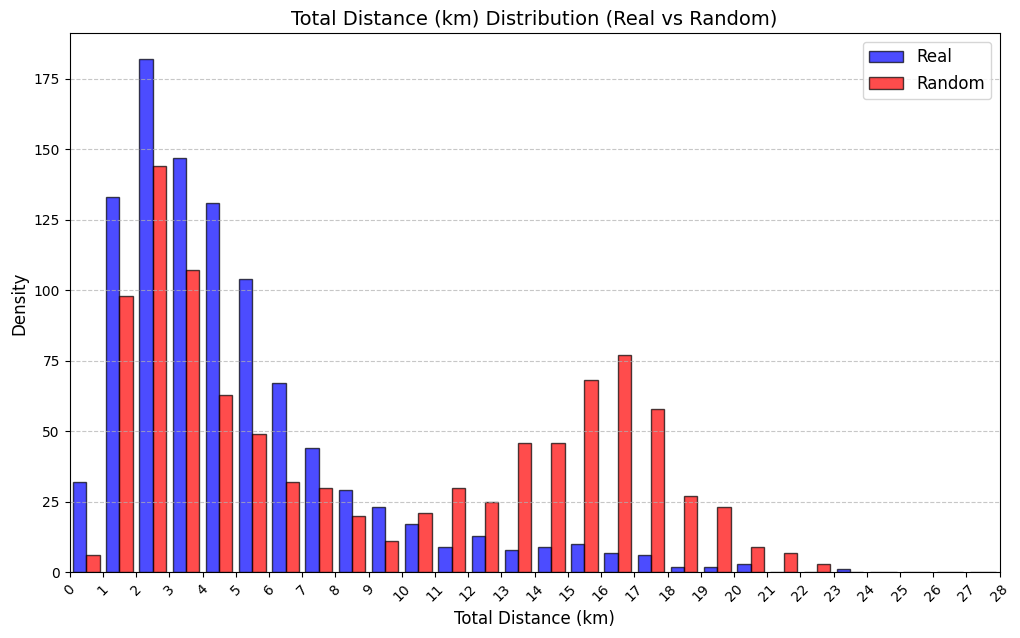
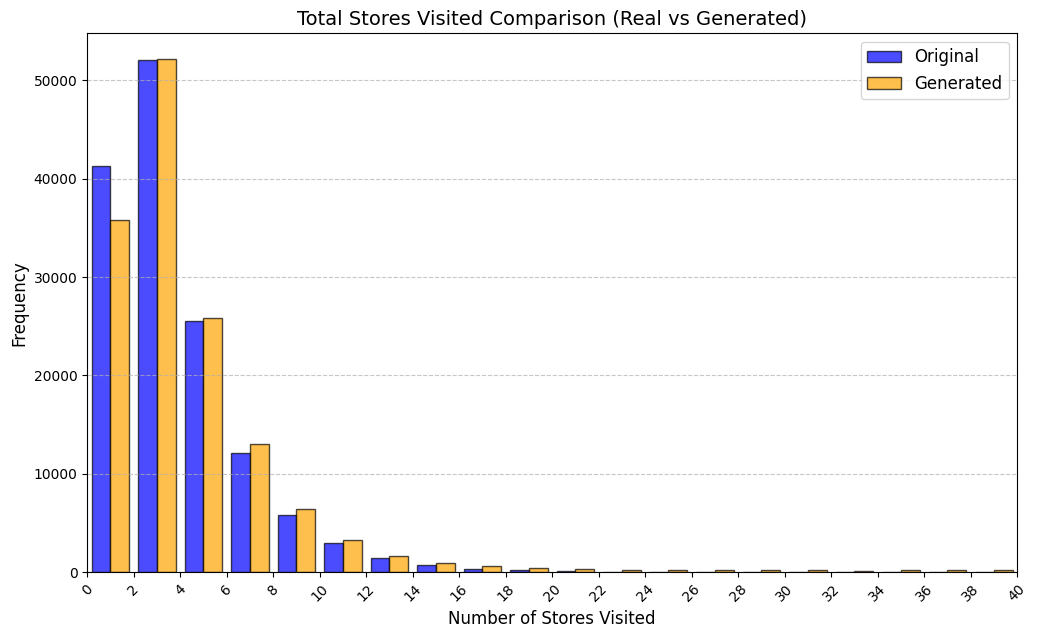
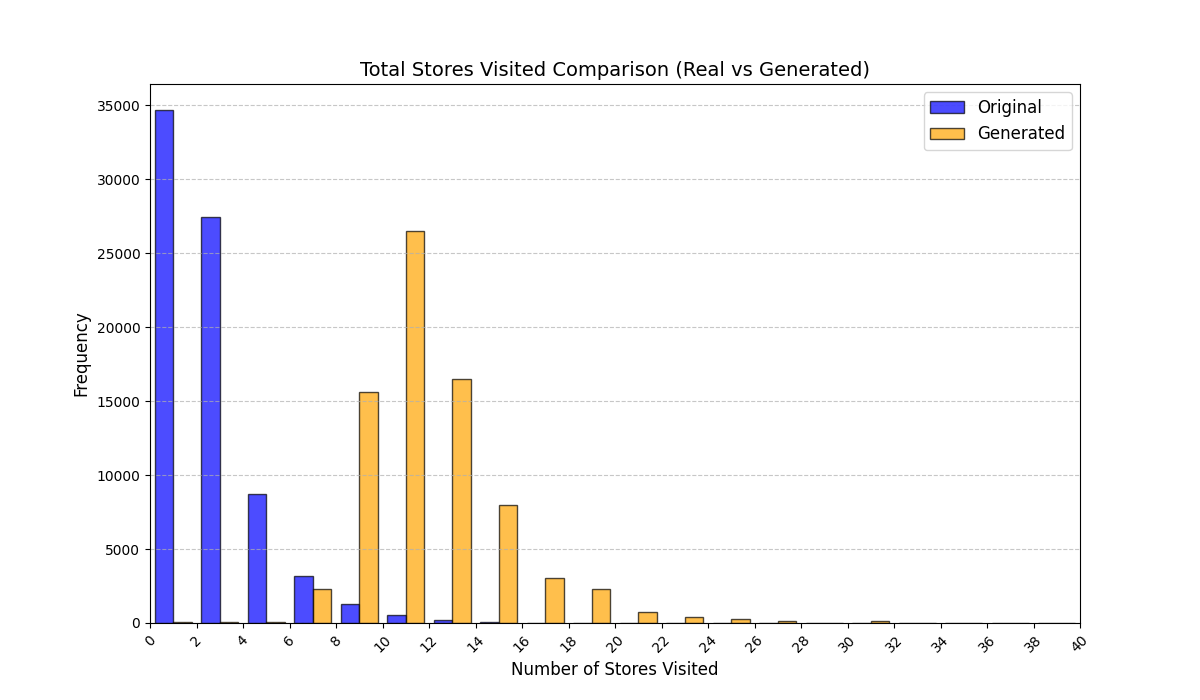
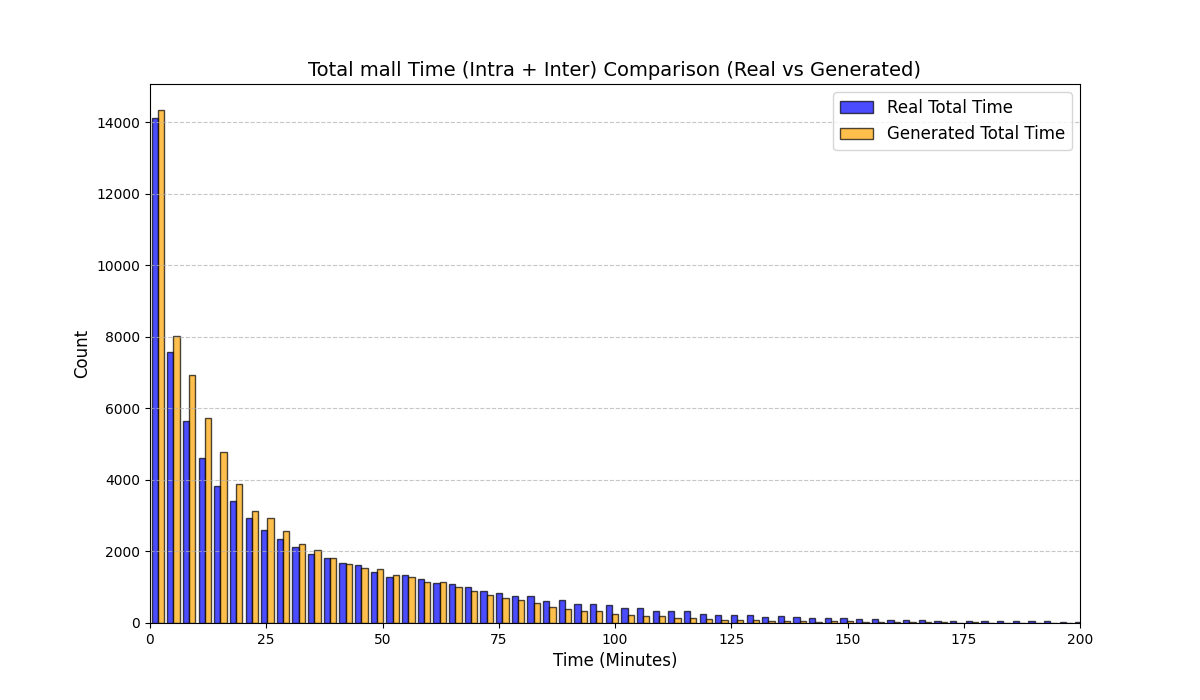
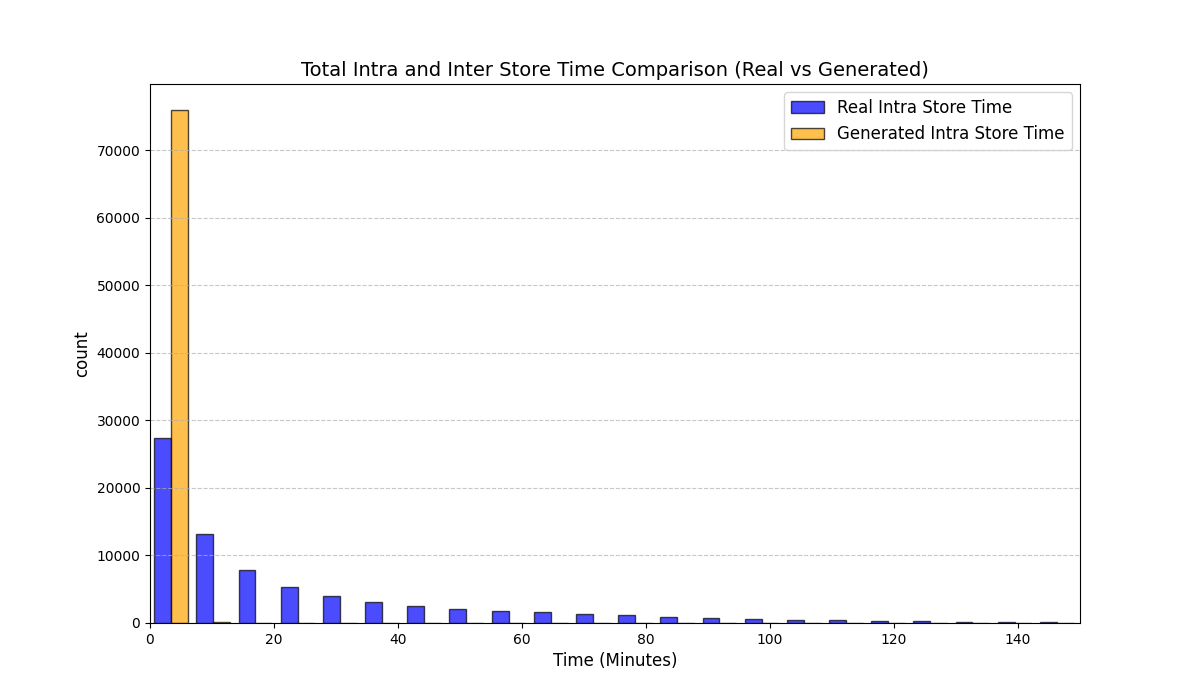
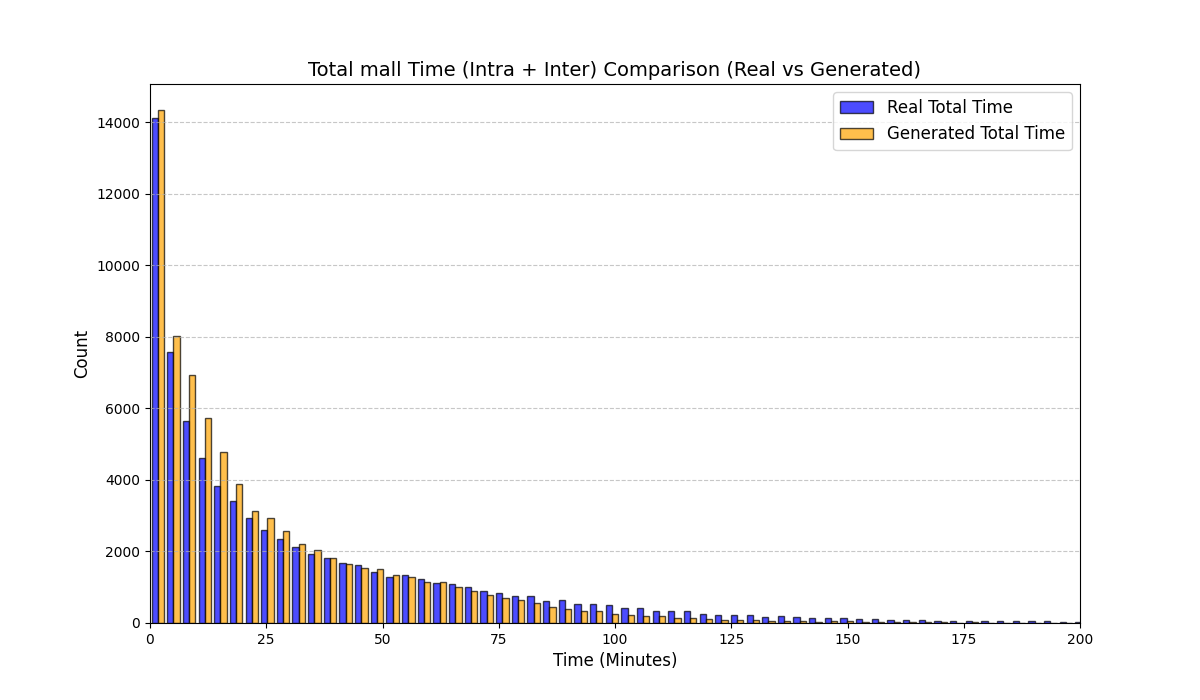
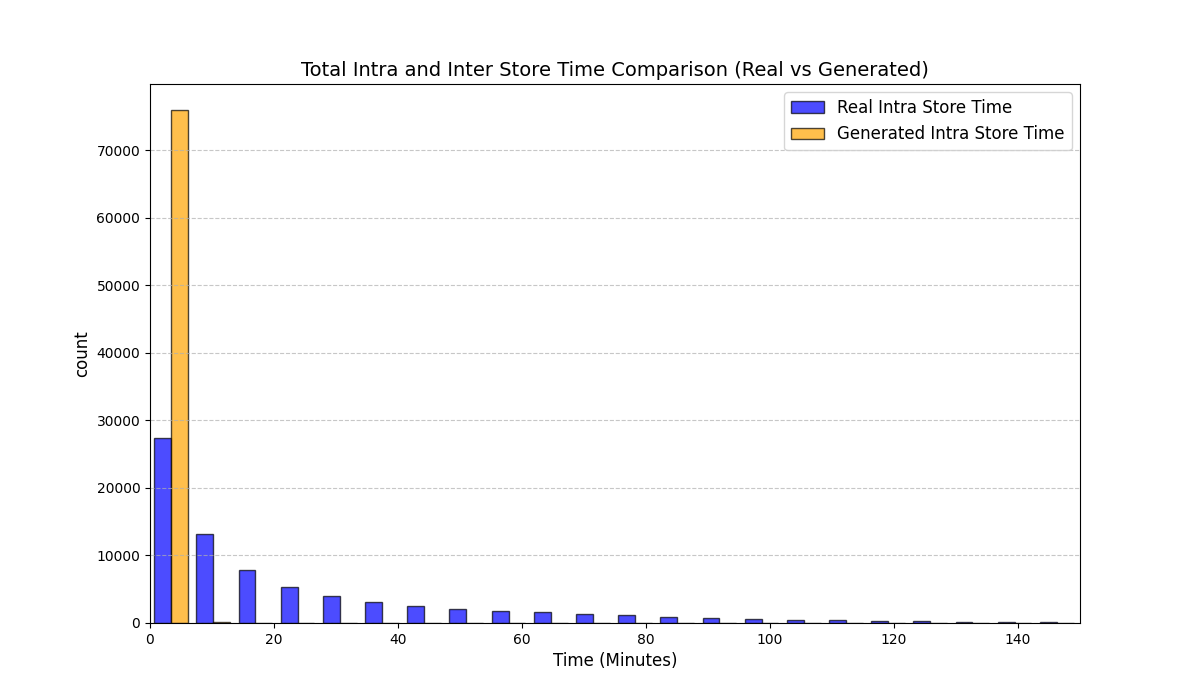
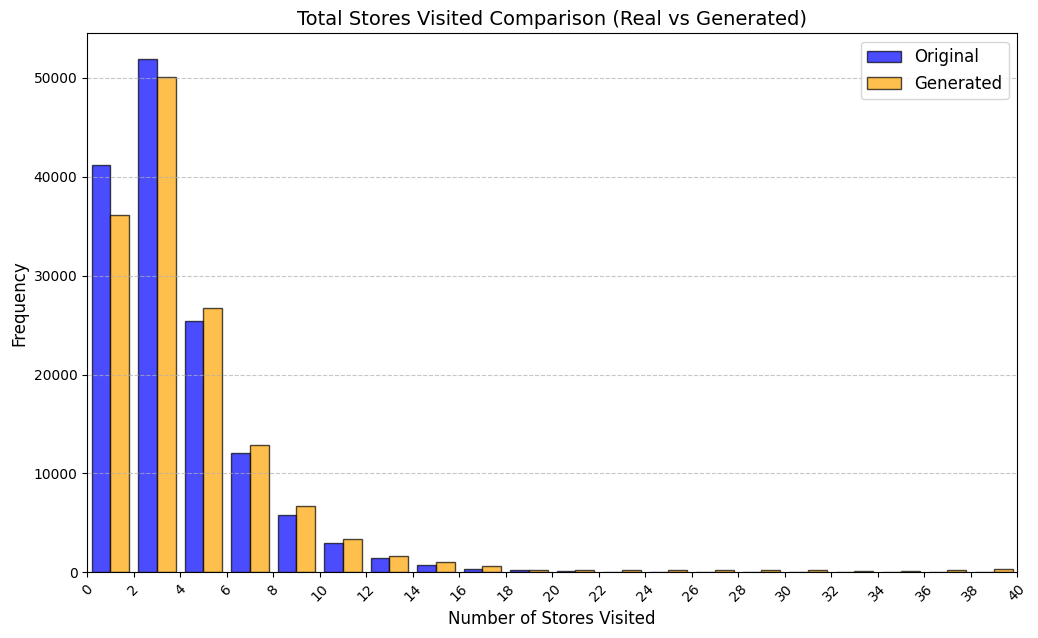
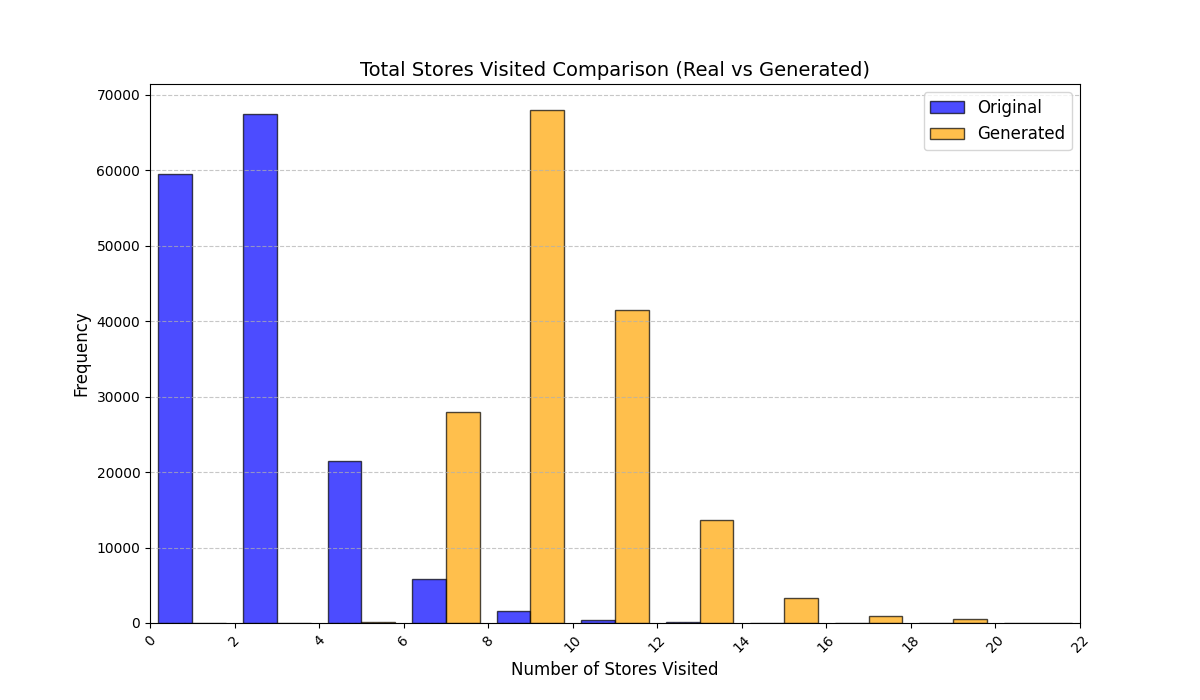
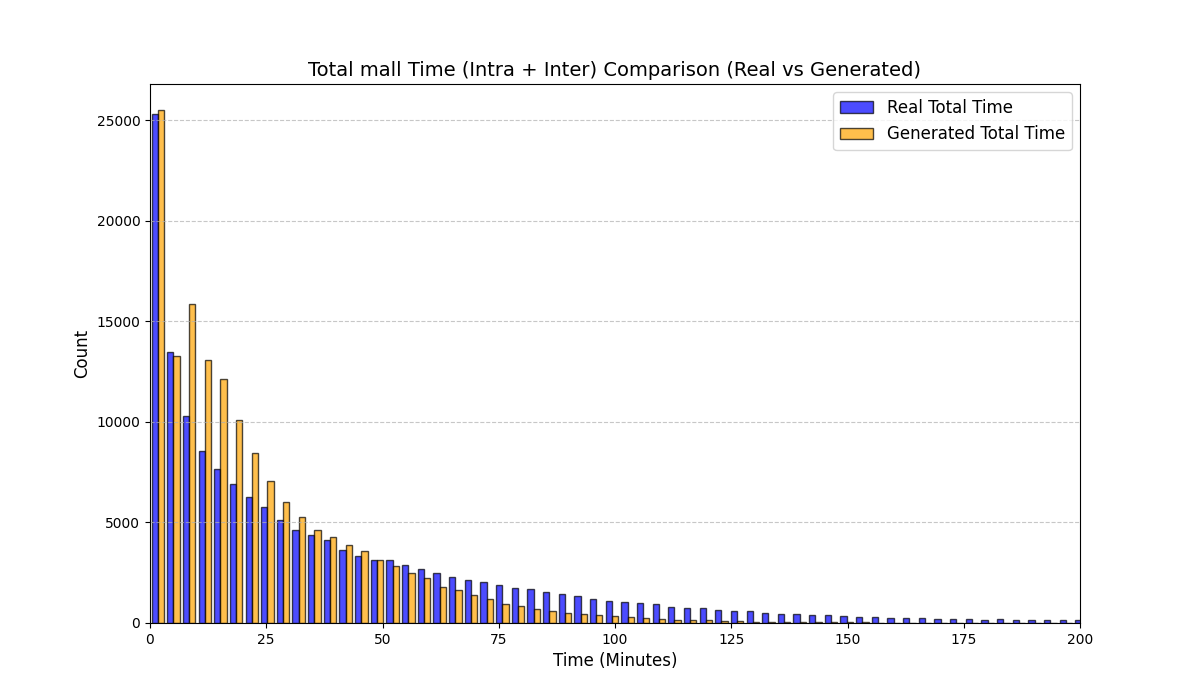
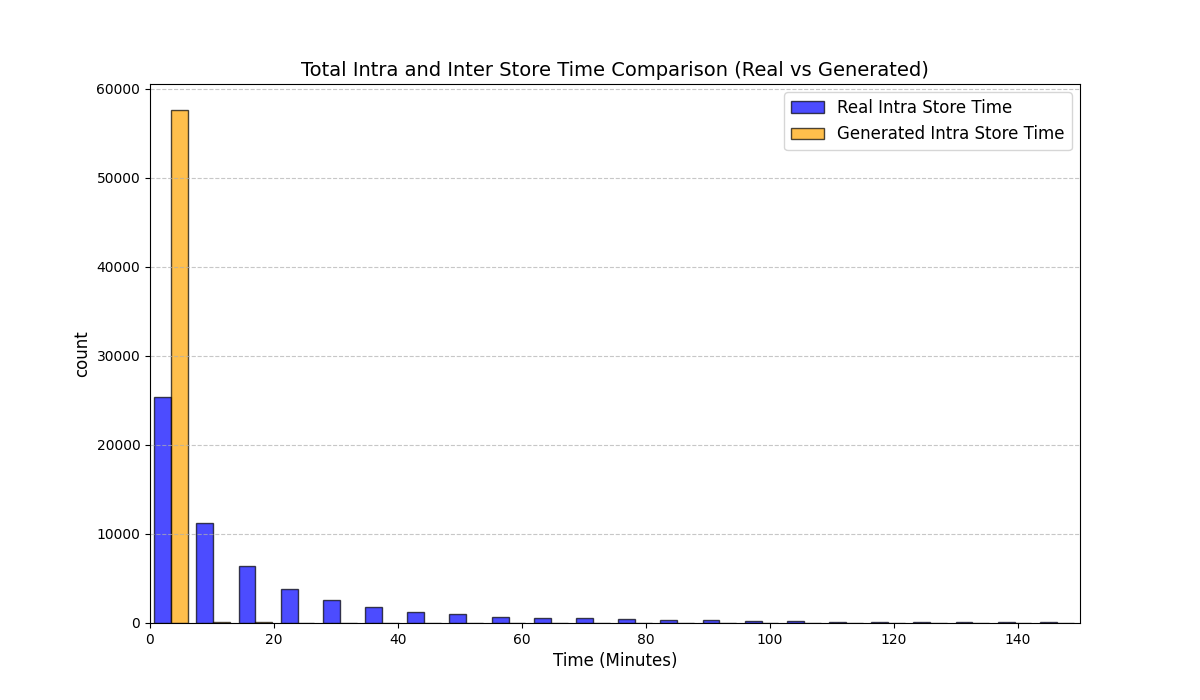
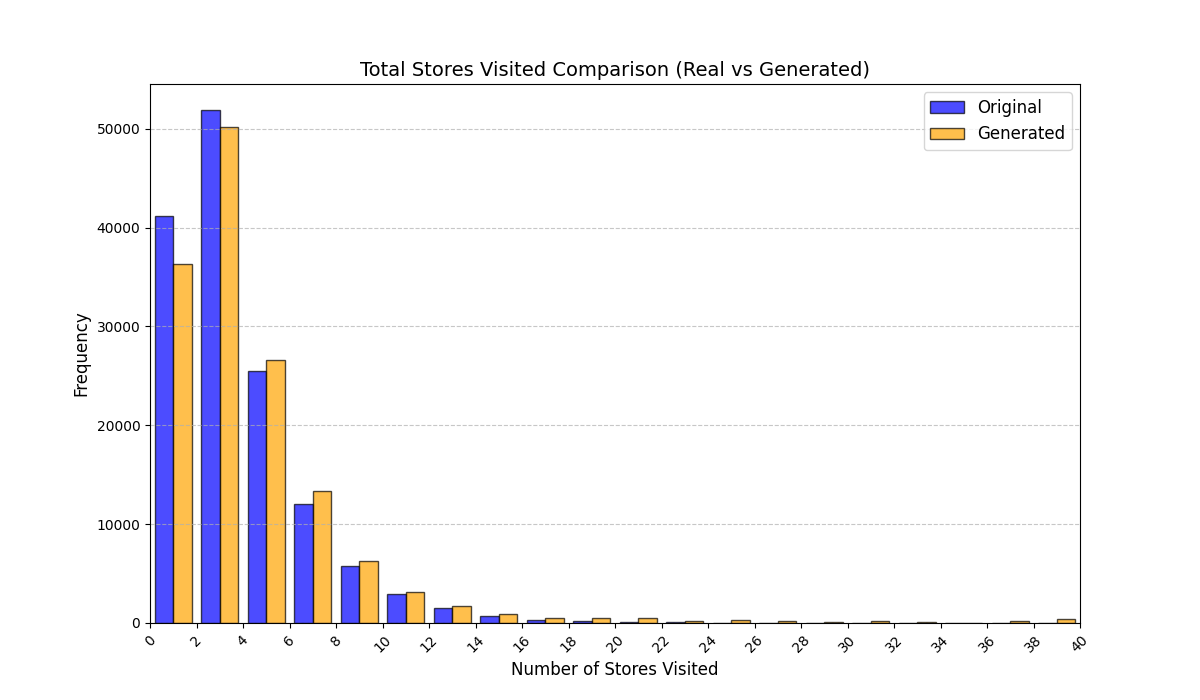
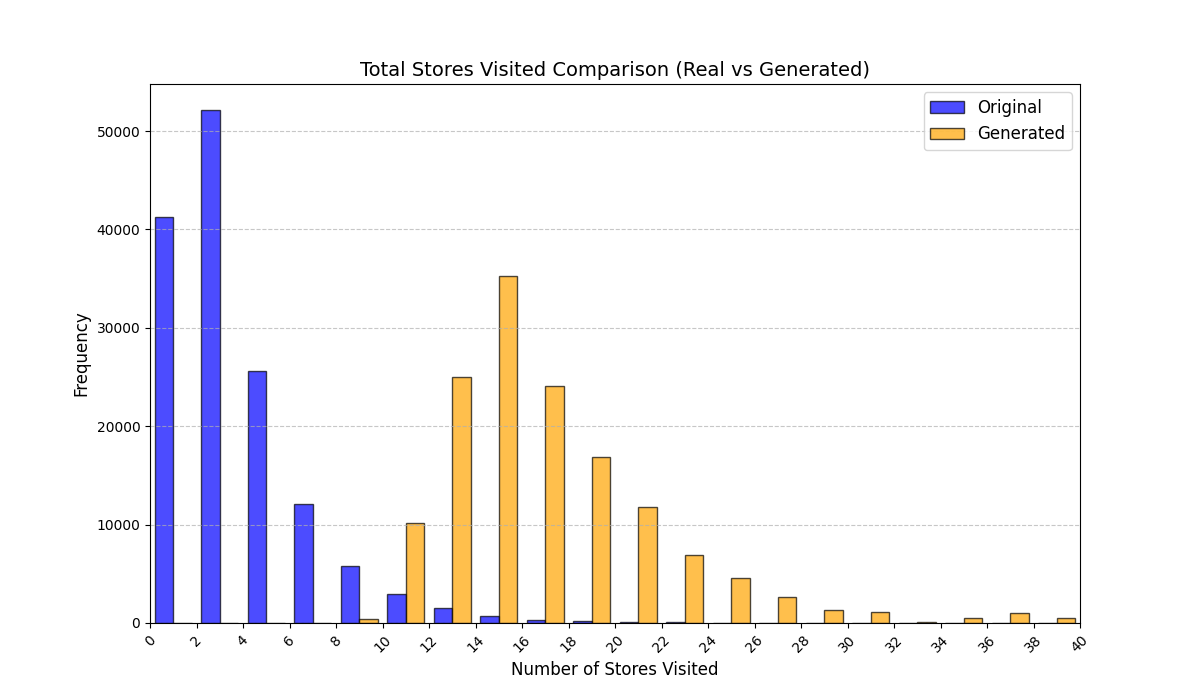
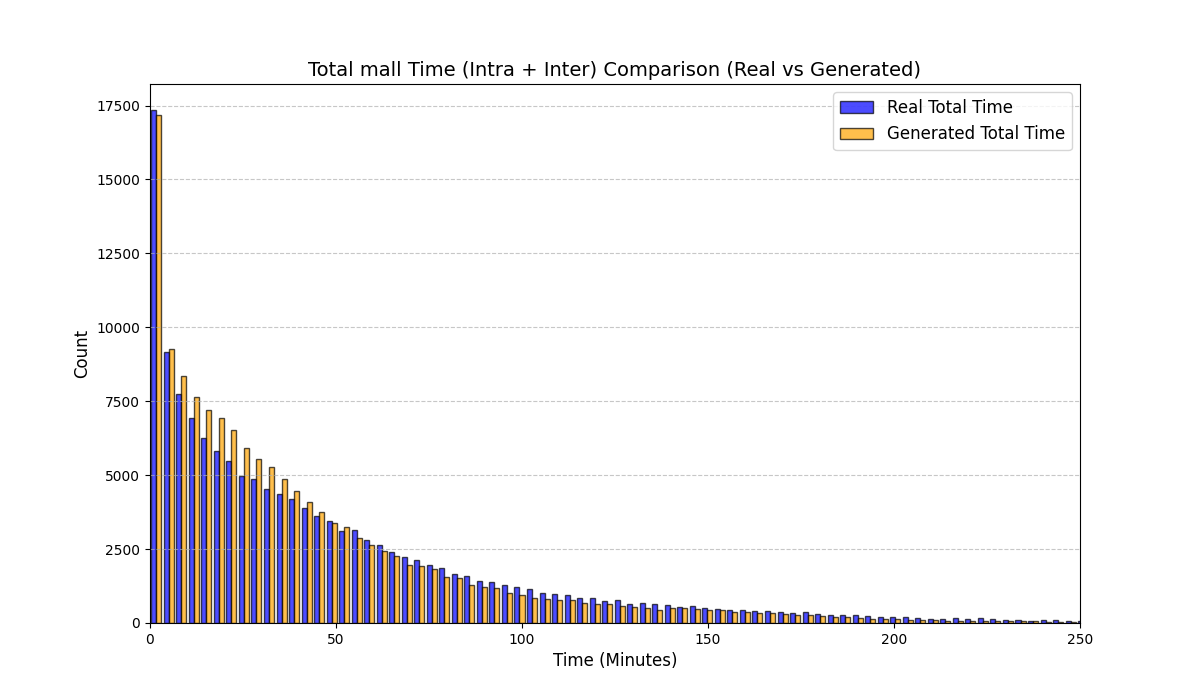
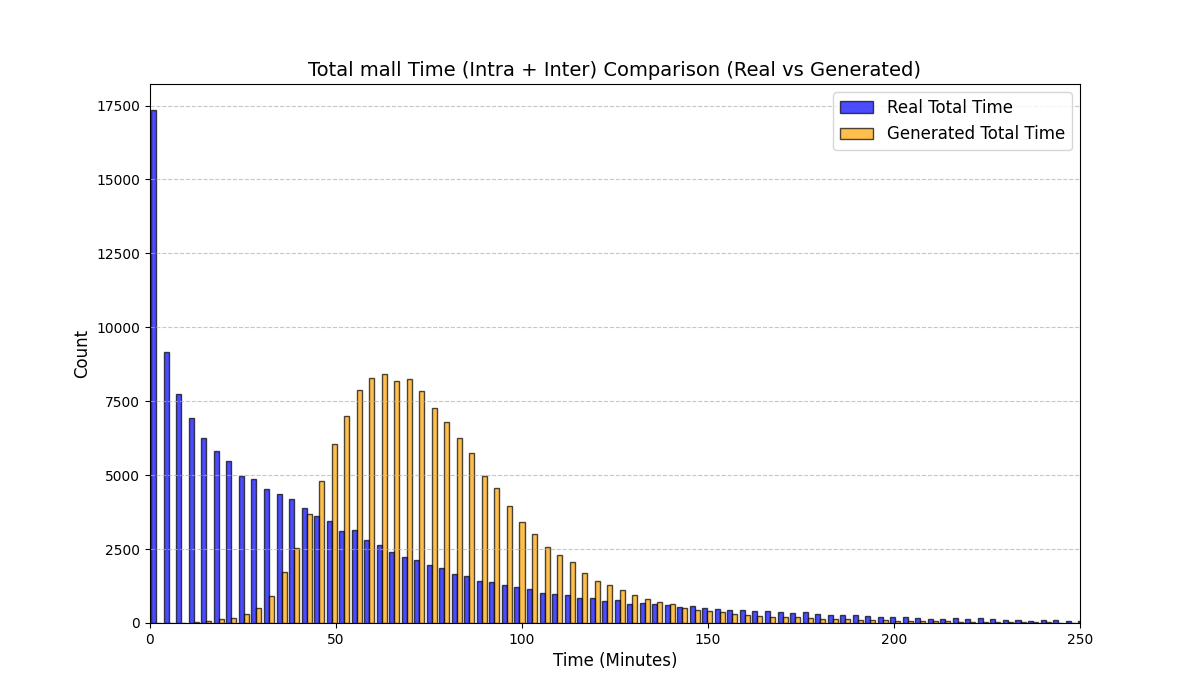
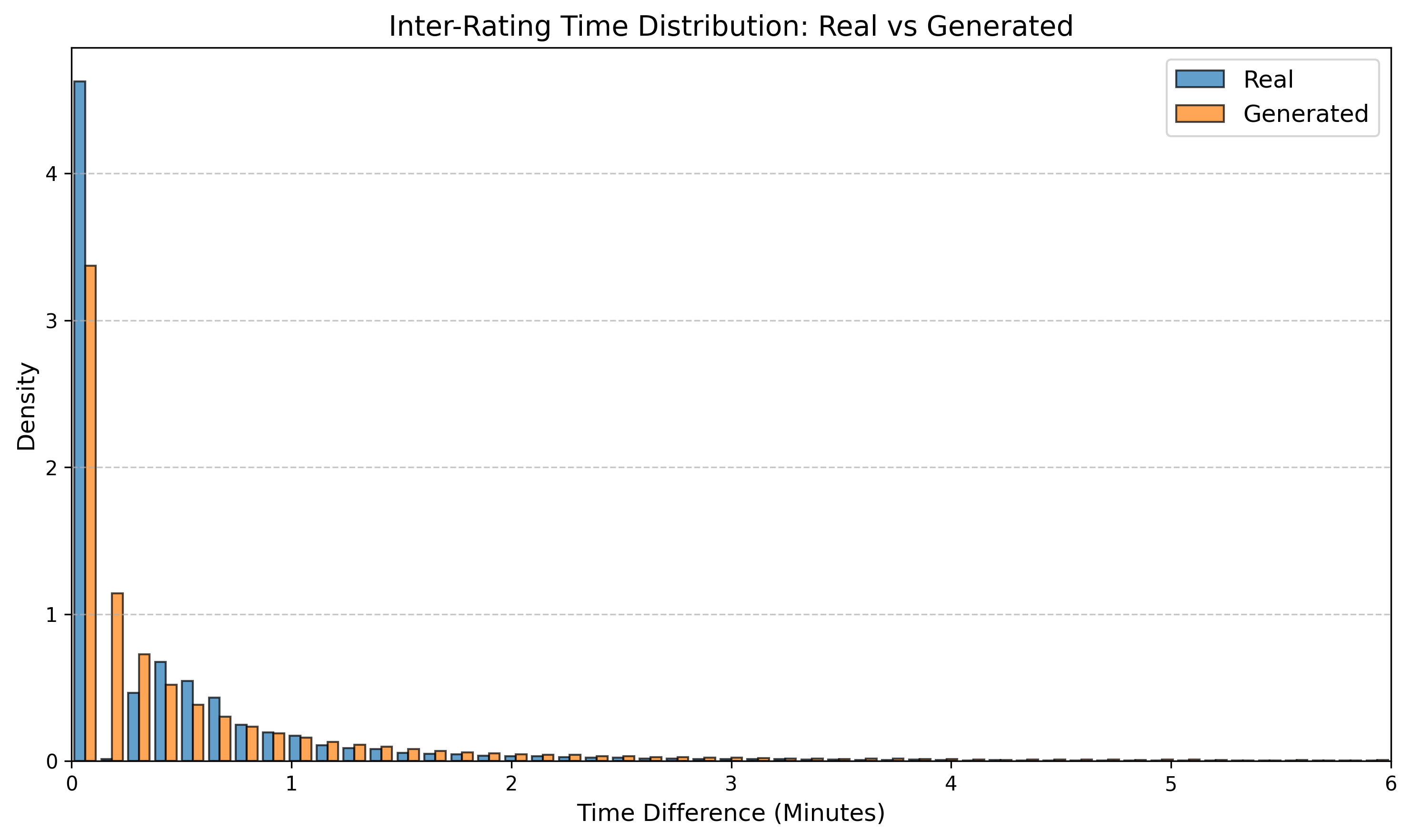
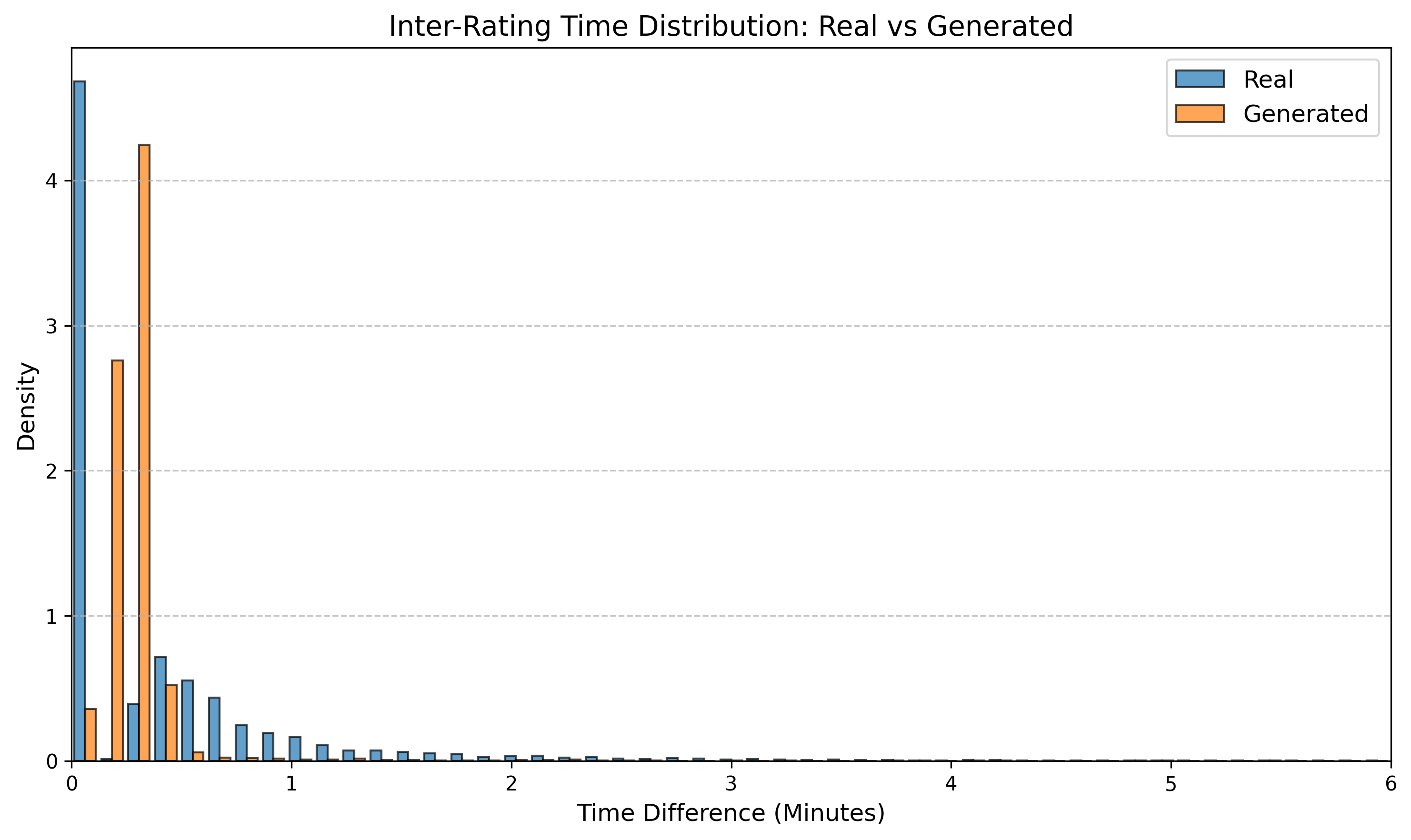
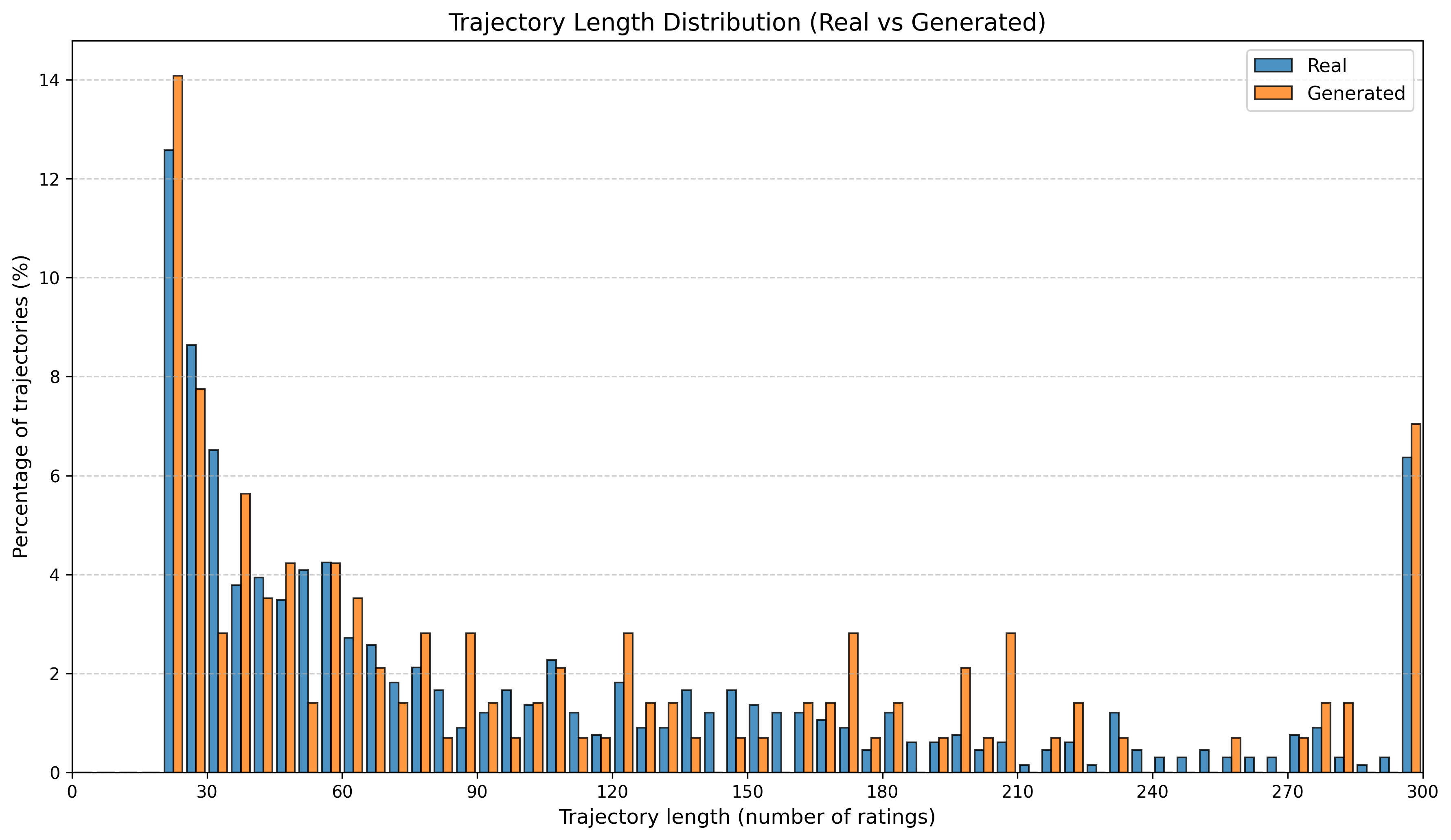
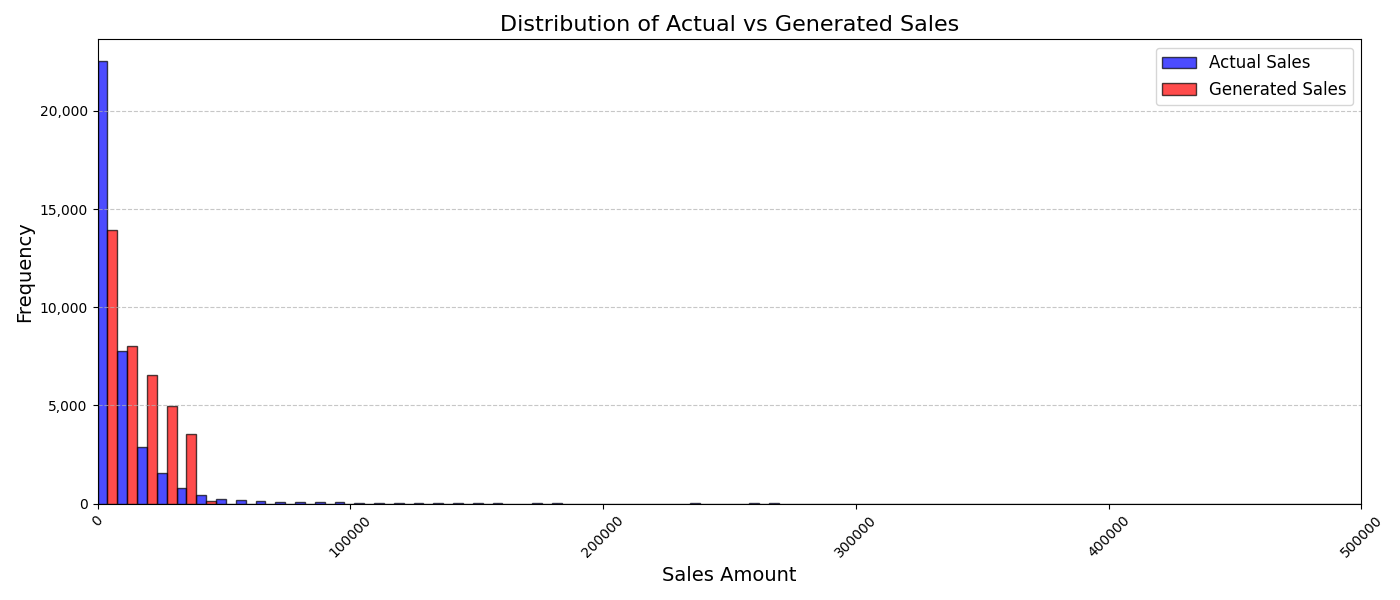
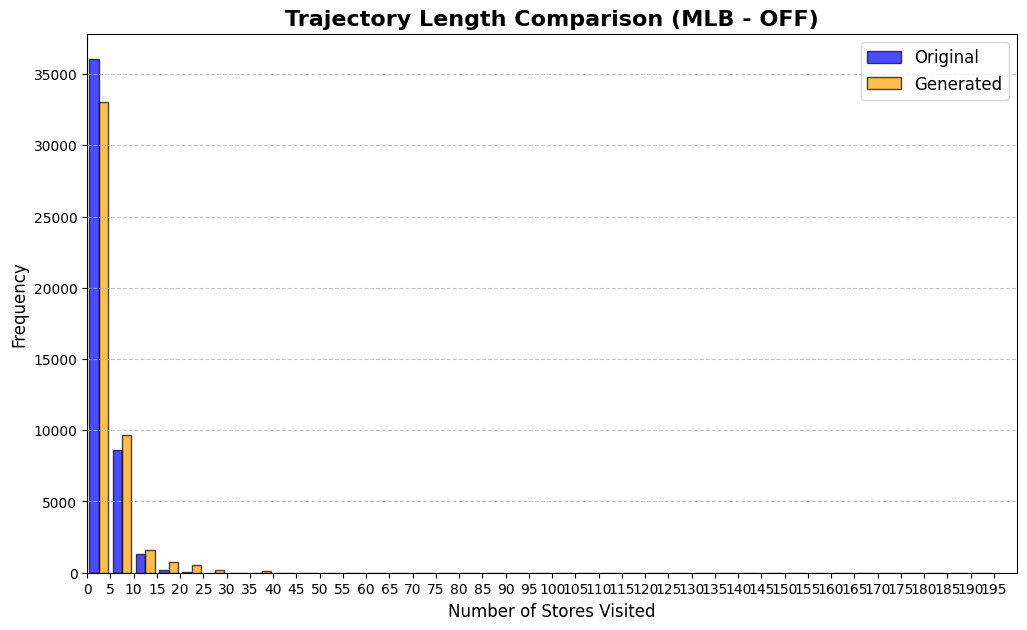
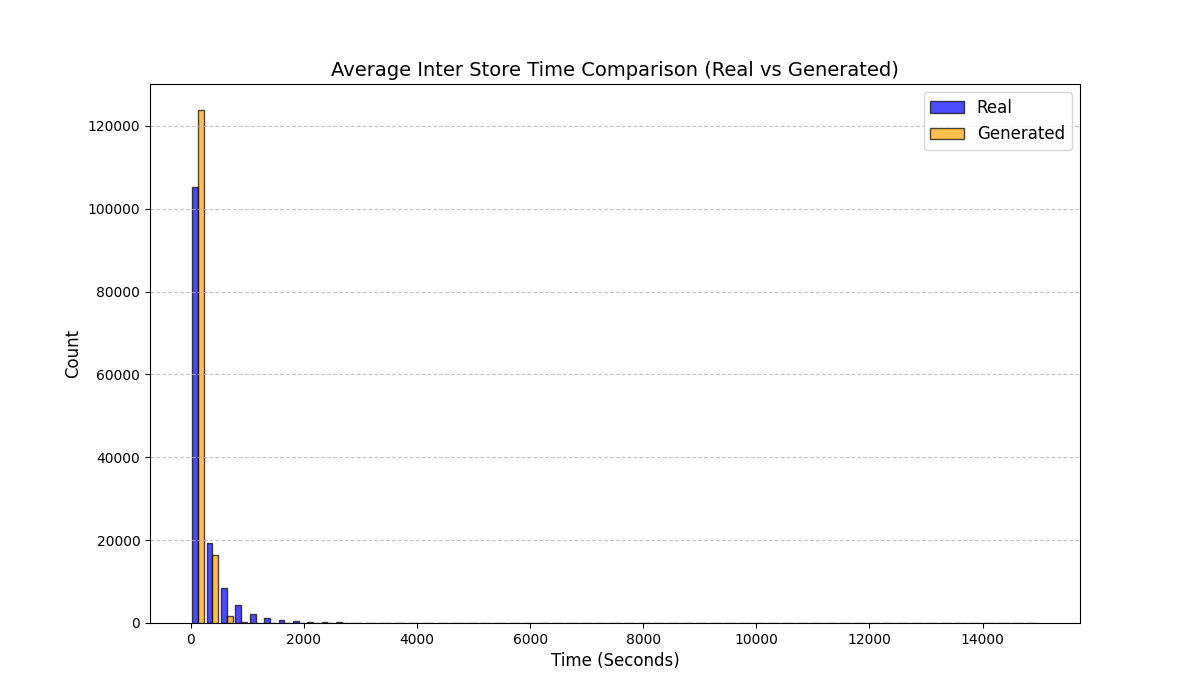
실험에서는 실제 몰 쇼핑 데이터와 4개의 공개 시퀀스 데이터셋(GPS 이동, 교육 로그, 전자상거래 클릭스트림, 영화 시청 기록)을 사용했다. 평가 지표는 각 데이터셋에 특화된 파생 변수(예: 매장 방문 비율, 이동 거리 분포, 학습 진도, 구매 전환율, 장르 선호도)의 KS‑통계량, Wasserstein 거리, 그리고 전체 로그우도 등을 포함한다. 모든 경우에서 LAS는 무작위 샘플링 대비 평균 5~12% 수준의 개선을 보였으며, 특히 길이 이질성이 극심한 GPS와 교육 로그에서 가장 큰 효과를 나타냈다. 또한, 학습 곡선이 더 부드럽고 수렴 속도가 빨라 실제 서비스 환경에서의 온라인 학습에도 유리함을 확인했다.
결론적으로, LAS는 모델 구조를 변경하지 않으면서도 배치 구성만으로 가변 길이 시퀀스 학습의 핵심 병목을 해소한다. 이는 디지털 트윈 구축, 시뮬레이션 기반 정책 설계, 그리고 다양한 도메인에서의 시계열·시퀀스 생성 작업에 바로 적용 가능한 실용적인 기법이다.
📄 논문 본문 발췌 (Excerpt)
📸 추가 이미지 갤러리