단기 전력 수요 예측(STLF)은 발전 단위의 운영, 경제적 배치 및 대비 스케줄링을 포함한 전력 그리드 운영에 근간을 두고 있습니다. 예측 오류는 중대한 결과를 초래합니다: 예측이 낮으면 연쇄적인 정전 위험이 있으며, 과대 예측은 불필요한 비용과 배출량 증가를 초래할 수 있습니다.

캘리포니아의 전력 그리드는 재생 에너지 시스템에 직면한 도전을 상징적으로 보여줍니다. 대규모 태양광 및 풍력 발전이 CAISO 계통에서 약 1/4의 에너지를 공급하며, 캘리포니아에서는 가정용 태양광 용량이 17GW를 넘었습니다. 이러한 비가시적인 발전은 ‘오리 곡선’을 만들어냅니다: 중간 시간대에 깊은 수요 감소와 저녁 시간대의 급격한 증가로 이어집니다. 이를 BMT 용량 확장으로 인해 연도별로 변화합니다. 이러한 비정상성은 기후 변화로 인한 극단적 날씨 사건이 역사적인 패턴을 벗어나는 비선형 수요 증가를 유발함으로써 더욱 복잡해집니다.

기존 예측 방법에는 근본적인 한계가 있습니다. 통계적 접근법(ARIMA)은 비선형 기상 의존성을 포착할 수 없습니다. 순환 네트워크(LSTMs)는 긴 시간 범위의 의존성에 대한 사라짐 경사를 이유로 어려움을 겪습니다. 트랜스포머 아키텍처는 이러한 문제를 해결하지만 $`O(n^2)`$ 복잡도를 도입하여 실제로 가능한 컨텍스트 길이가 제한됩니다.

상태 공간 모델(SSMs)은 신뢰성을 향상시키는 유망한 접근법입니다. 선형 $`O(n)`$ 스케일링을 통해 Mamba는 확장된 역사적 컨텍스트와 낮은 추론 지연을 가능하게 합니다. 그러나 지역 그리드 예측에서 안전 마진을 유지할 수 있는지 여부는 아직 연구되지 않았습니다.

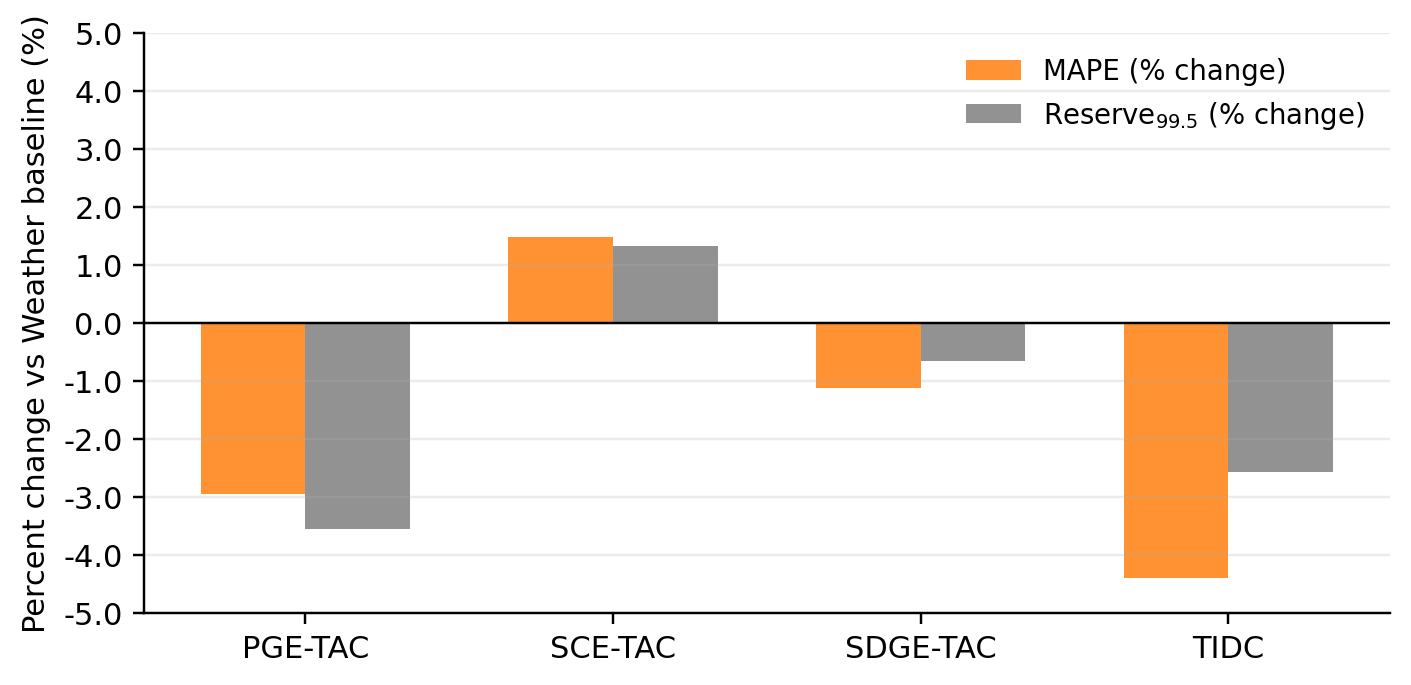
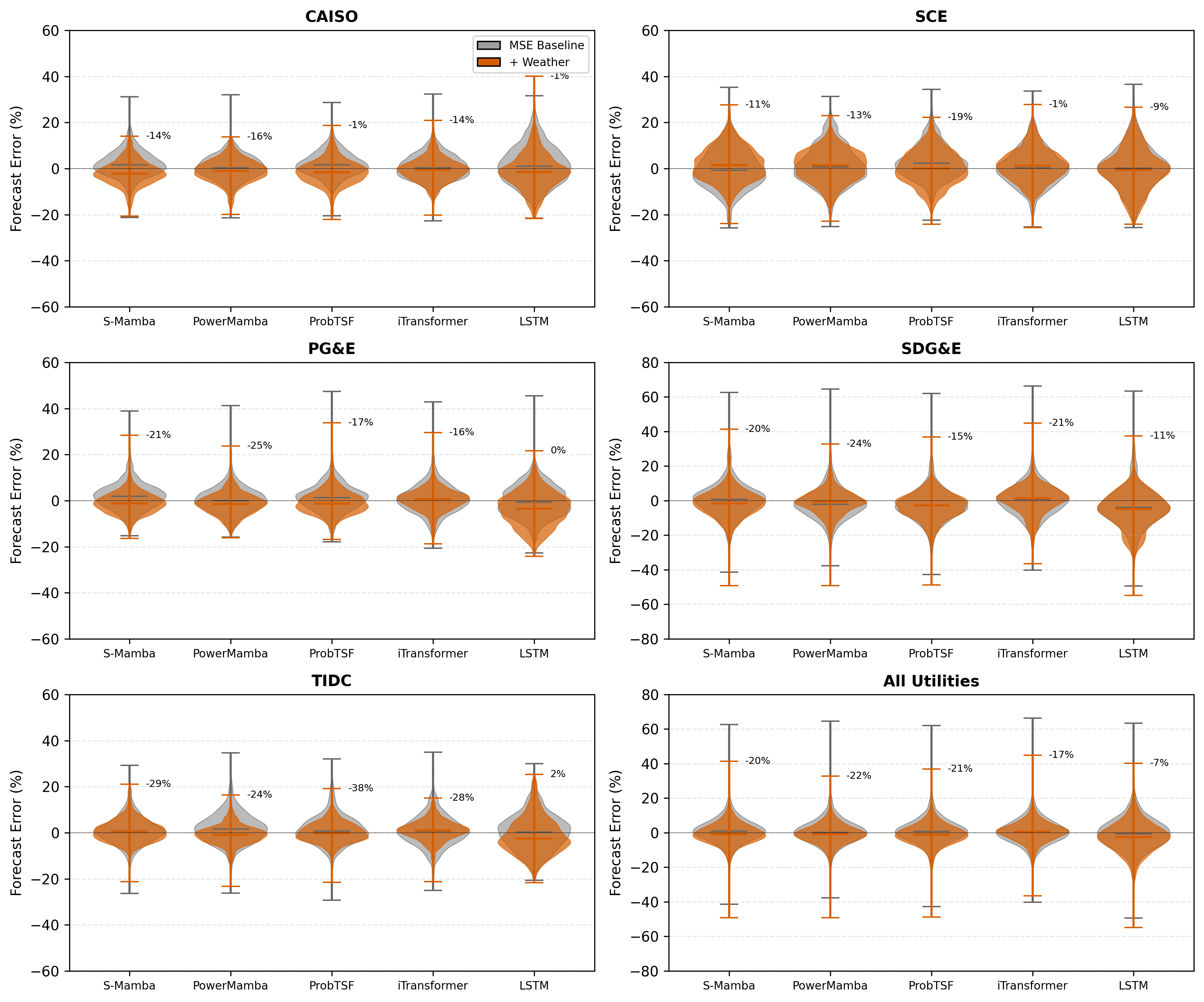
우리는 Mamba 아키텍처의 시스템적인 평가를 통해 캘리포니아 전력 그리드 예측의 신뢰성을 분석합니다. iTransformer와 기초 모델인 Chronos와 비교하여, 평가의 초점을 순수한 정확성에서 운영 안전성으로 이동시킵니다. 우리의 결과는 예측 정확도만으로는 운용적 위험을 충분히 대표하지 못함을 강조합니다: 예를 들어, MAPE가 비슷하더라도 모델 간에 Reserve$`_{99.5}^{\%}`$의 차이가 크다는 것입니다. 또한 우리는 명시적인 기상 통합이 안전성을 향상시키는 데 중요함을 보여줍니다 (섹션 6.3 참조).

기여

캘리포니아 전력 그리드 예측에서 대칭 정확도 지표를 넘어 운영자에게 중요한 신뢰성을 제공하기 위해 다음과 같은 기여를 합니다:

1. Grid-Specific Evaluation Framework: 우리는 비대칭 운영 비용을 포착하고 시스템적인 예측 과대 평가로 인한 ‘위장된 안전성’을 방지하는 운용적 위험 지표(예: Under-Prediction Rate, tail Reserve$`_{99.5}^{\%}`$ 요구사항, Bias/OPR 진단)를 공식화합니다 (섹션 2.3 참조).

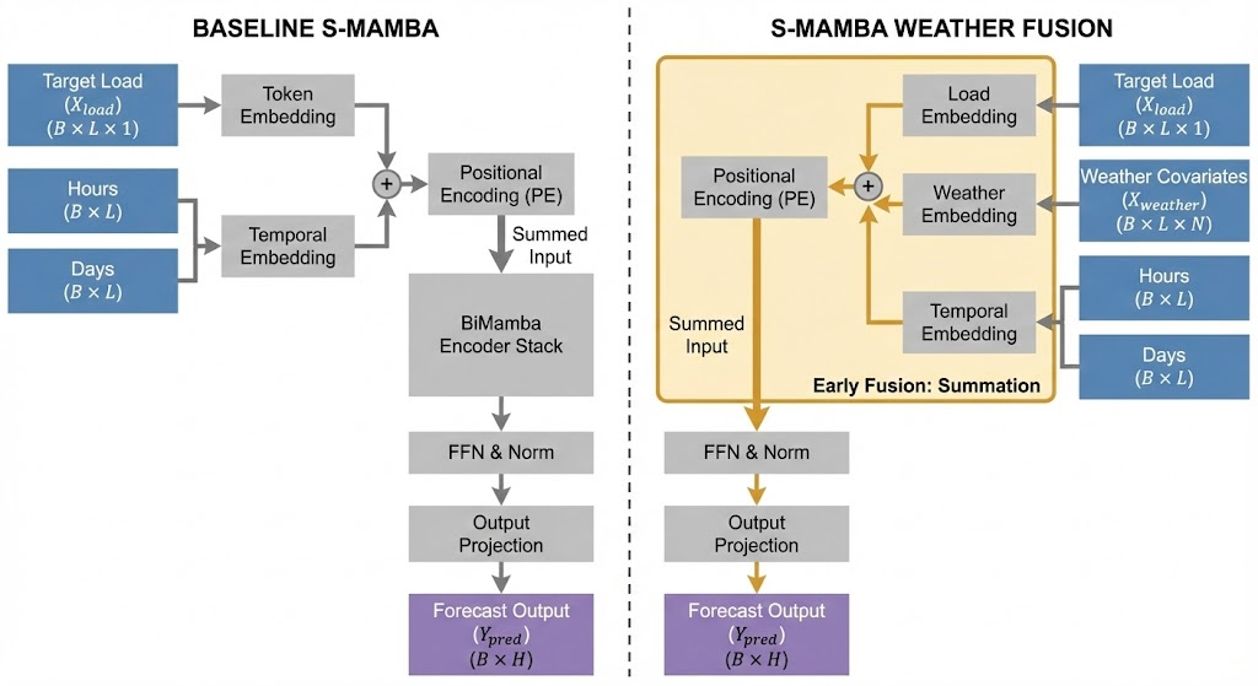
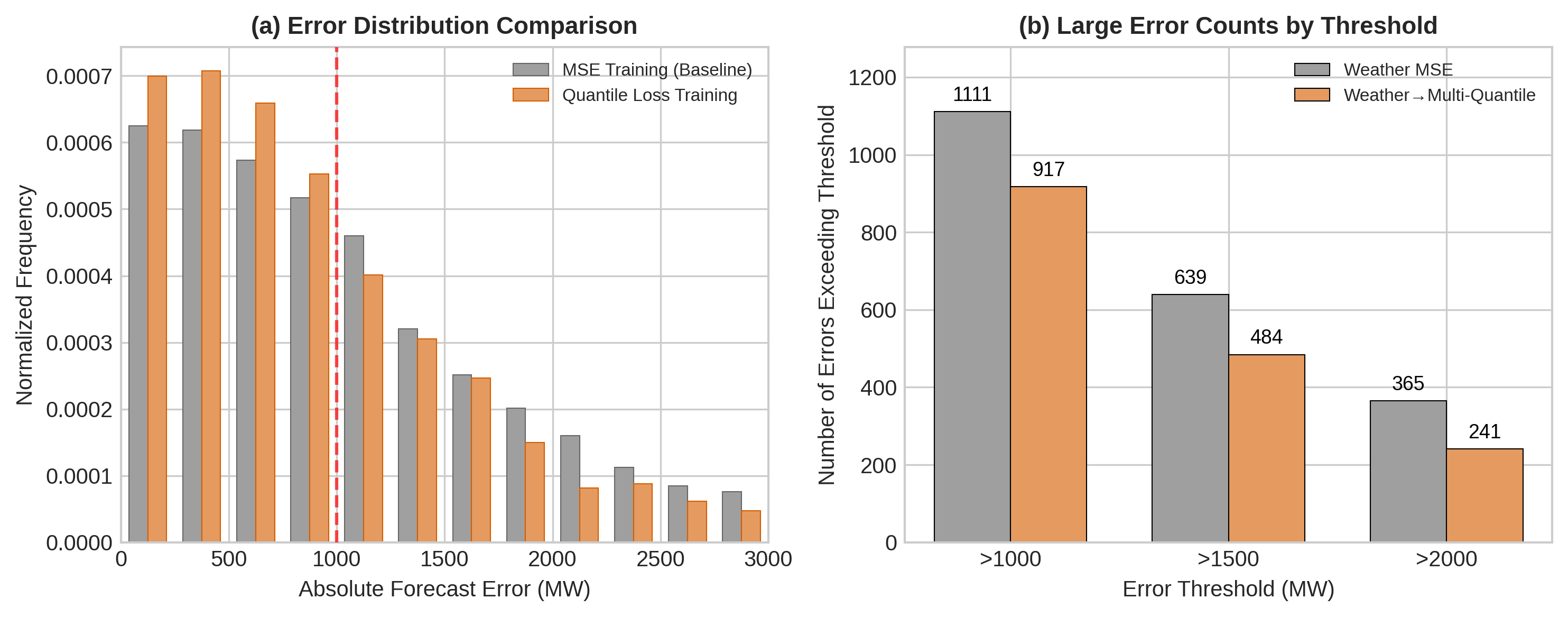
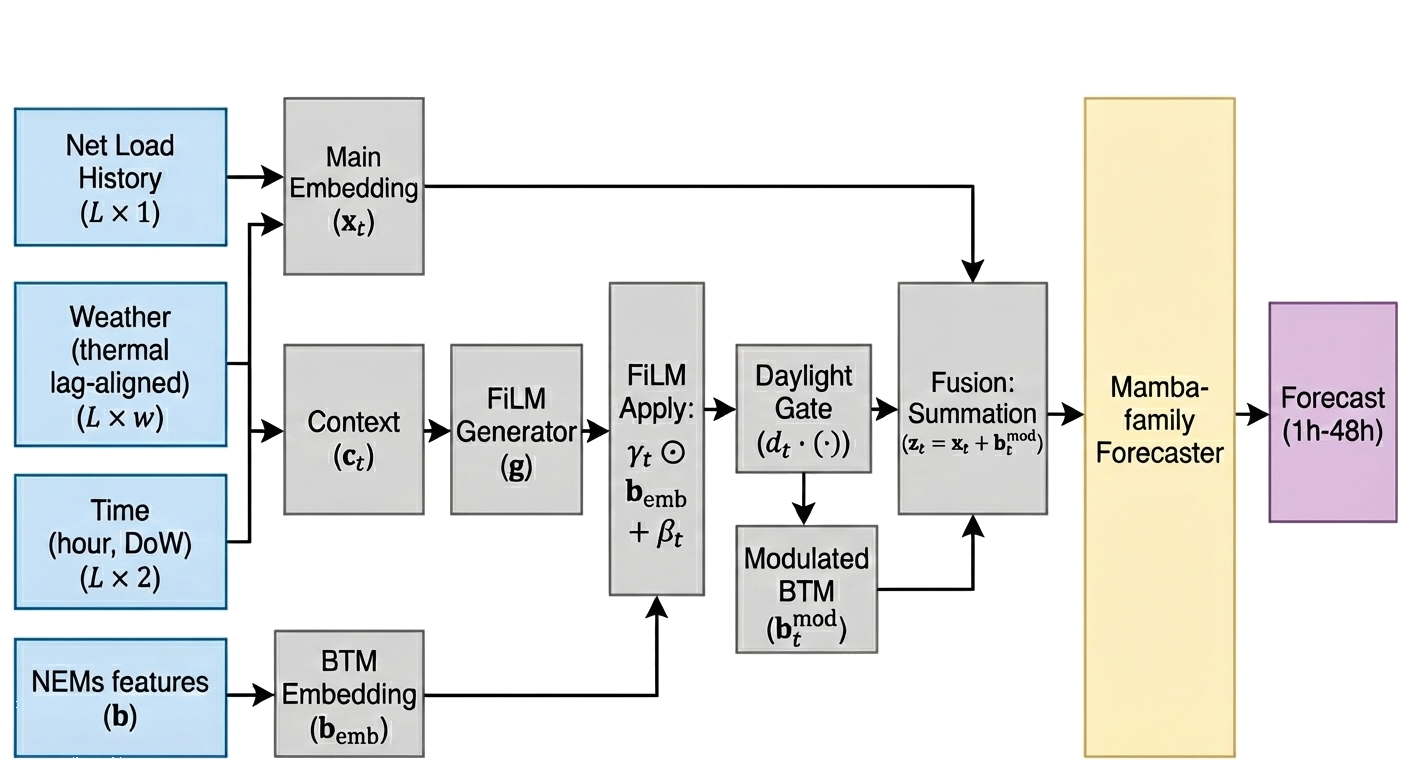
2. Weather Integration for SSMs: 우리는 Mamba 아키텍처에 대한 열적 지연 일치 기상 통합 전략을 개발하고 시스템적으로 평가하여 오류 분포를 좁히고 극단적인 오류를 줄여 안정성을 향상시킵니다 (섹션 4.2, 섹션 6.3 참조).

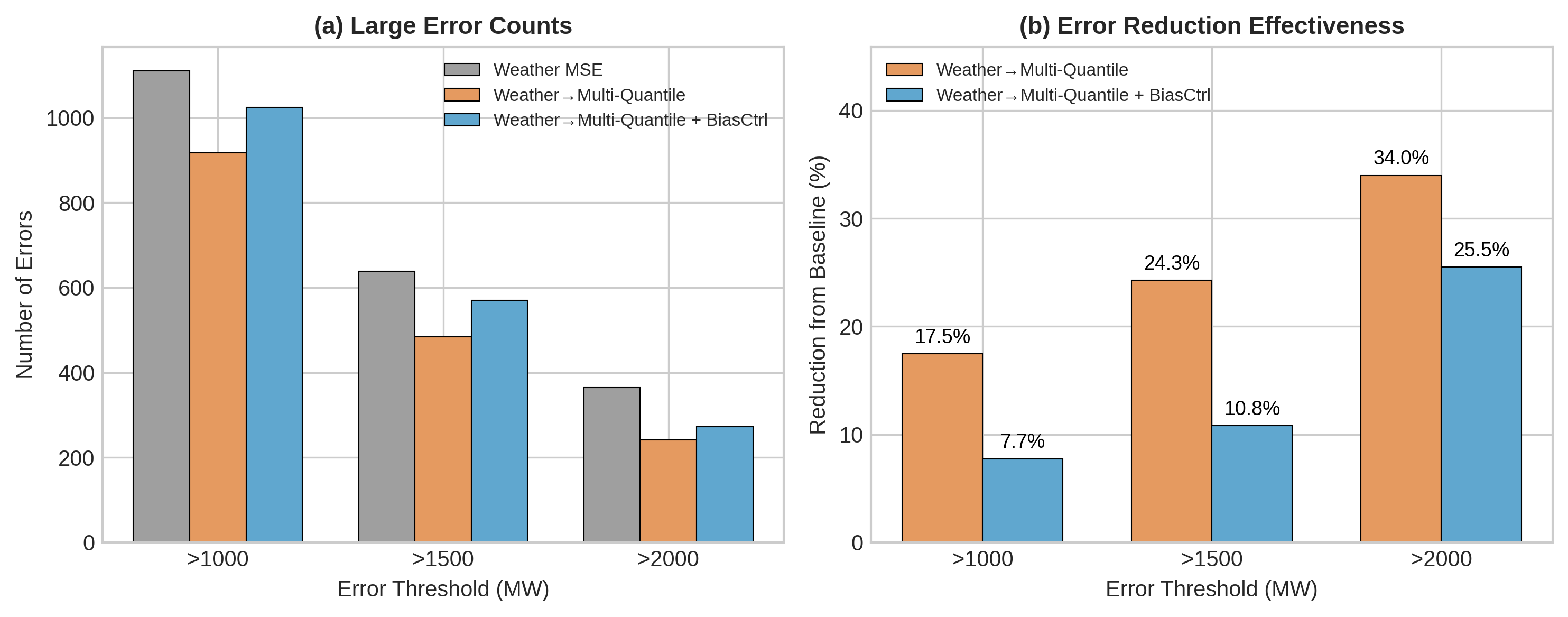
3. Loss vs. Safety Analysis: 우리는 확률적 보정(다중 양위 핀볼)이 고정 평가 분할에서 큰 오류 이벤트를 줄일 수 있지만 편향/OPR을 명시적으로 제약하고 꼬리 위험 지표와 함께 보고하지 않으면 시스템적 과대 예측을 유발할 수 있음을 보여줍니다 (섹션 6 참조).

배경

상태 공간 모델

상태 공간 모델(SSMs)은 연속 시간 동역학계를 통해 순차 데이터를 모델링하는 원칙적인 프레임워크를 제공합니다. 일반 선형 SSM은 다음과 같은 상미분 방정식으로 정의됩니다:

\begin{equation}
h'(t) = Ah(t) + Bx(t), \quad y(t) = Ch(t) + Dx(t)
\end{equation}

여기서 $`x(t) \in \mathbb{R}`$는 입력 신호, $`h(t) \in \mathbb{R}^N`$는 차원이 $`N`$인 잠재 상태이고, $`y(t) \in \mathbb{R}`$은 출력입니다. 행렬 $`A \in \mathbb{R}^{N \times N}`$, $`B \in \mathbb{R}^{N \times 1}`$, $`C \in \mathbb{R}^{1 \times N}`$, 및 $`D \in \mathbb{R}`$는 학습 가능한 매개변수입니다.

샘플 데이터에 대한 이산 시간 계산을 위해 연속 SSM은 이산화되어야 합니다. 0차 보드 디스커테이제이션을 사용하여 시간 단계 $`\Delta`$로, 이산시간 SSM은 다음과 같습니다:

\begin{equation}
h_k = \bar{A}h_{k-1} + \bar{B}x_k, \quad y_k = Ch_k
\end{equation}

여기서 $`\bar{A} = \exp(\Delta A)`$이고 $`\bar{B} = (\Delta A)^{-1}(\exp(\Delta A) - I) \cdot \Delta B`$입니다.

선택적 상태 공간: 전통적인 SSM은 시간 불변(LTI) 매개변수를 사용합니다. Mamba 아키텍처는 이러한 매개변수가 입력에 따라 변하도록 선택 메커니즘을 도입합니다:

\begin{equation}
B_k = s_B(x_k), \quad C_k = s_C(x_k), \quad \Delta_k = \text{softplus}(s_\Delta(x_k))
\end{equation}

여기서 $`s_B`$, $`s_C`$ 및 $`s_\Delta`$는 학습된 투영입니다. 이 선택성은 모델이 관련 정보를 필터링하고 불필요한 컨텍스트를 잊게 함으로써 기존 SSM의 근본적인 한계를 해결합니다.

그리드 데이터에 대한 적합성: Wang et al.의 최근 분석은 Mamba가 트랜스포머보다 우수하게 수행하는 조건을 식별했습니다: “많은 변수들 중 대부분이 주기적"인 데이터셋입니다. 그리드 부하 데이터는 이 특성을 정확히 충족합니다 - 여러 공간 노드를 통해 일주일, 일주일, 연간 주기가 있는 신호입니다. Mamba의 선택적 상태 메커니즘은 이러한 리듬 의존성을 인코딩하고 확률적인 잡음을 필터링합니다.

계산 복잡도: SSMs는 $`O(n)`$ 복잡도를 달성하며 트랜스포머의 $`O(n^2)`$보다 효율적입니다. Menati et al은 멀티 스케일 그리드 동역학을 포착하는 데 240시간 이상의 컨텍스트 윈도우가 최적임을 보여주었으며, 이는 표준 트랜스포머에 대해 계산적으로 불가능한 길이입니다.

부하 예측 기본

정의 및 시각: 단기 전력 수요 예측(STLF)은 몇 시간에서 며칠 미래의 전력 수요를 예측하는 것을 포함합니다. 다른 예측 범위는 다양한 운영 목적을 위해 사용됩니다: 실시간 배치에 1시간, 발전 단위 조정에 46시간, 그리고 장기 시장 운영에 1224시간.

다중 주기성: 전력 부하는 강한 다중 주기 패턴(일간, 주간, 연간)을 보입니다. 우리의 선택은 240시간 (10일) 컨텍스트 길이를 통해 최소한 한 개의 완전한 주기 사이클을 포착하도록 합니다.

평가 지표: 전력 부하 예측에는 평균 절대 백분율 오차(MAPE)가 표준 지표로 사용됩니다:

\begin{equation}
\text{MAPE} = \frac{100}{n} \sum_{i=1}^{n} \left| \frac{y_i - \hat{y}_i}{y_i} \right|
\end{equation}

그리드 특화 평가 지표

MAPE 및 RMSE와 같은 표준 지표는 예측 오류를 대칭적으로 처리합니다: 100MW의 과대 예측은 100MW의 부족 예측과 동일하게 처벌됩니다. 그러나 그리드 운영자에게 이러한 오류들의 경제적 및 신뢰성적인 결과는 근본적으로 비대칭적입니다.

운영 비용 비대칭

• 과대 예측 (False Positive): 모델이 실제 수요보다 높은 부하를 예측하면 유틸리티는 과도한 발전을 커밋하게 됩니다. 이로 인해 재료 낭비, 중단 비용 등 경제적 손실이 발생하지만 시스템 안정성에 거의 위협되지 않습니다.

• 부족 예측 (False Negative): 모델이 실제 수요보다 낮은 부하를 예측하면 유틸리티는 공급 부족을 겪게 될 가능성이 있습니다. 이로 인해 비싼 빠른 발전 설비(예: 피커 플랜트)를 배치하거나 긴급 전력을 시장 가격으로 구입해야 하며, 극단적인 경우 롤링 정전을 시작할 수 있습니다.

따라서 표준 MAPE는 운영 검증에 부적합합니다. 이를 해결하기 위해 우리는 다음의 그리드 특화 지표를 제안합니다:

제안된 지표

• Under-Prediction Rate (UPR):
  예측이 실제보다 낮은 이벤트의 빈도는 실시간 상향 배치가 필요할 확률을 나타냅니다:

\begin{equation}
    \text{UPR} = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(y_i > \hat{y}_i) \times 100\%
\end{equation}

• Over-Prediction Rate (OPR):
  과대 예측 이벤트의 빈도는 예약된(중앙값) 예측에서 시스템적 과대 평가를 드러냅니다:

\begin{equation}
    \text{OPR} = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(\hat{y}_i > y_i) \times 100\%
\end{equation}

• Upward Reserve Requirement (Reserve$`_{99.5}^{\%}`$):
  예측 오차 분포의 99.5%를 커버하기 위해 필요한 추가 상향용 용량입니다:

\begin{equation}
    \text{Reserve}_{99.5}^{MW} = \text{Percentile}_{99.5}\!\left(\max(0, y - \hat{y})\right)
\end{equation}

\begin{equation}
    \text{Reserve}_{99.5}^{\%} = 100 \times \text{Percentile}_{99.5}\!\left(\max\left(0, \frac{y - \hat{y}}{\hat{y}}\right)\right)
\end{equation}

$`\text{Reserve}_{99.5}^{MW}`$를 점 예측에 추가하면 평가된 시간대의 과거 부족 예측 이벤트의 99.5%를 커버합니다. MW와 퍼센티지 형태로 보고: MW는 정규화 없이 보고되며, 퍼센티지 형태는 점 예측에 추가할 수 있는 직접적인 해석을 제공합니다.

동기 부여 사례

이 지표들의 운영 현실성을 설명하기 위해 실제 결과 (후술될 표 2 참조)를 살펴봅니다. 꼬리 위험 및 편향 진단이 서로 다른 방향으로 움직일 수 있습니다. 예를 들어, 꼬리에 초점을 맞춘 손실로 학습된 모델은 $`Reserve_{99.5}^{\%}`$를 줄이는 것처럼 보이지만 전체 예측을 과대 평가함으로써 이를 달성할 수 있습니다.

편향 제약 확률적 목표

UPR 및 꼬리 예비 요구 사항은 우수한 평가 지표입니다만, 직접 최적화하기에는 차별화되지 않고 어려울 수 있습니다. 이러한 간극을 메우기 위해 학습 중에 사용되는 Bias-Constrained Probabilistic Objective (섹션 4.3 참조)를 차별 가능한 대용물로 사용합니다.

가치 지향 학습

전통적인 예측 목표(MSE/MAPE)는 예측 정확도가 결정 품질을 대신한다고 가정합니다. 그러나 그리드 운영에서는 비용 함수가 매우 비대칭적이고 제한적입니다. ‘가치 지향’ 또는 ‘스마트 예측-그리고 최적화’ 패러다임은 예측과 하류 최적화 사이의 분리를 도전하며, 모델이 최종 운영 비용을 최소화하도록 학습되어야 함을 제안합니다. 이론적으로는 최적이나 전반적인 형식 최적화 솔버를 내장하는 완전한 엔드-투-엔드 양레벨 최적화는 대규모 딥러닝에 대해 계산적으로 해결하기 어렵습니다. 본 연구에서는 이러한 철학의 확장 가능한 실현을 채택합니다: 전체 확장형 형식 최적화 솔버를 내장하는 대신 운영 가치 함수를 직접 bias-constrained probabilistic objective (섹션 4.3 참조)에 인코딩합니다.

관련 연구

딥러닝을 통한 시계열 분석

딥러닝은 비선형 관계를 모델링하기 위한 능력으로 인해 통계적 방법(ARIMA, SVR)을 단기 전력 수요 예측에서 대체했습니다. 현재의 연구는 긴 컨텍스트 다변량 모델링을 위한 두 가지 주된 패러다임에 초점을 맞추고 있습니다:

트랜스포머 기반 접근법: 트랜스포머는 전역 주의를 계산하여 장기 의존성을 포착할 수 있지만 $`O(n^2)`$ 복잡도를 가지고 있습니다. 다변량 데이터 처리에 두 가지 주요 전략이 등장했습니다:

• 채널 독립성: PatchTST와 같은 모델은 다변량 시간 시리즈를 독립적인 채널로 취급하고 패치로 분할합니다. 이는 복잡도를 줄이고 현재 트랜스포머 정확도의 최고 수준을 나타내지만, 변수 간의 명시적 상호 연관성을 포착하지 못합니다.

• 다변량 주의: iTransformer와 같은 모델은 시간 단계를 특징으로 임베딩하여 변수 간의 상호 연관성을 명시적으로 모델링합니다. 우리는 이러한 직접적인 공간 관련성 모델링을 통해 Mamba와 대조하는 주요 벤치마크로 iTransformer를 연구하고 있습니다.

효율적 시퀀스 모델링(SSMs): 상태 공간 모델은 근본적으로 다른 접근법을 제공합니다. 트랜스포머의 2차원 전역 주의 대신 Mamba와 같은 SSMs는 입력에 따라 선택하는 순환 모드를 사용하여 선형 $`O(n)`$ 스케일링을 달성합니다. 이 효율성은 동일한 하드웨어에서 유사한 시간 범위의 계절 패턴을 포착하기 위한 훨씬 긴 컨텍스트 윈도우를 가능하게 합니다.

선형 모델: 최근 연구는 시계열 예측에 대해 딥러닝이 필요하지 않음을 주장하고 있습니다. DLinear은 간단한 선형 모델이 표준 벤치마크에서 트랜스포머 성능을 일치하거나 초과할 수 있음을 보여주며, 이는 아키텍처 복잡성에 대한 질문을 제기합니다.