스케일러블 데이터 기반 도달 가능성 분석 및 제어 쿠프만 연산자와 컨포멀 보장
📝 원문 정보
- Title: Scalable Data-Driven Reachability Analysis and Control via Koopman Operators with Conformal Coverage Guarantees
- ArXiv ID: 2601.01076
- 발행일: 2026-01-03
- 저자: Devesh Nath, Haoran Yin, Glen Chou
📝 초록 (Abstract)
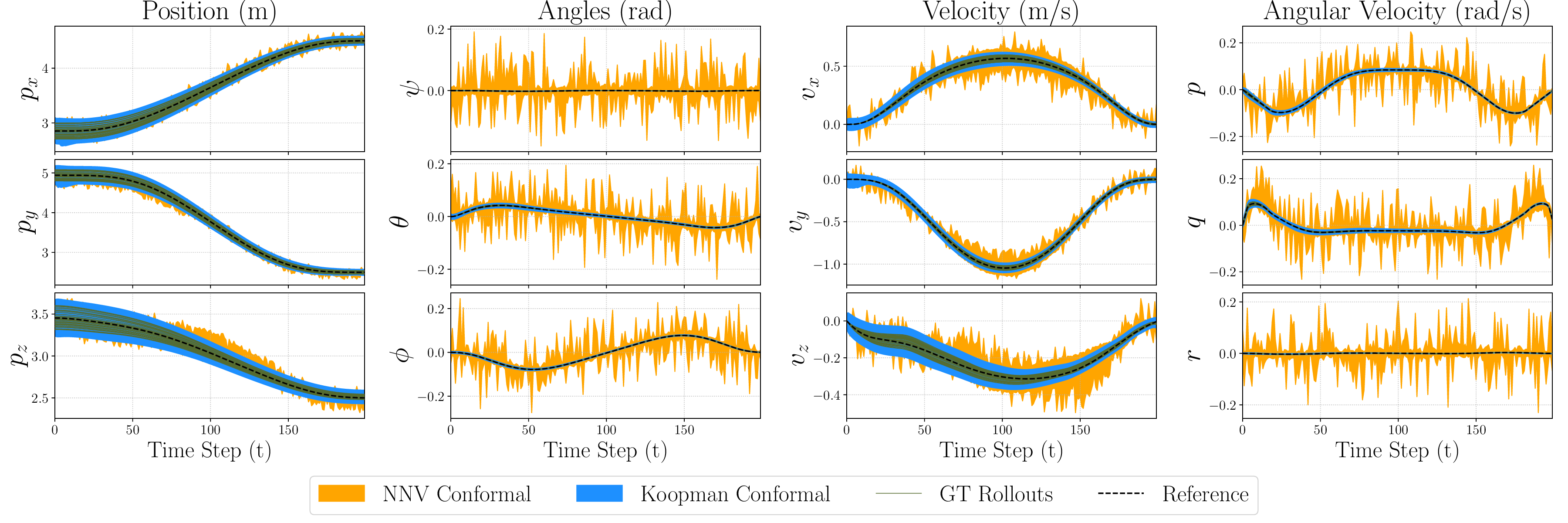
우리는 알려지지 않은 비선형 시스템에 대한 확률적 데이터 기반 안전 검증을 위한 스케일러블 도달 가능성 프레임워크를 제안한다. 쿠프만 이론과 신경망(NN) 리프팅 함수를 결합해 시스템의 근사 선형 표현을 학습하고, 이 선형 공간에서 선형 컨트롤러를 설계하여 레퍼런스 궤적 분포를 추적하도록 한다. 닫힌 루프의 도달 가능 집합은 리프팅된 공간에서 효율적으로 계산되며, NN 검증 도구를 이용해 원래 상태 공간으로 매핑된다. 쿠프만 동역학과 실제 시스템 사이의 모델 불일치를 포착하기 위해 컨포멀 예측을 적용해 통계적으로 유효한 오류 경계를 생성하고, 이 경계를 도달 가능 집합에 팽창시켜 사용자가 지정한 확률로 실제 궤적이 포함되도록 보장한다. 이러한 경계는 레퍼런스 전반에 걸쳐 일반화되어 재계산 없이 재사용이 가능하다. 11차원 Hopper, 28차원 Swimmer와 같은 고차원 MuJoCo 과제 및 12차원 쿼드콥터 실험에서 기존 방법에 비해 도달 가능성 커버리지, 계산 효율성, 보수성 측면에서 향상된 결과를 보여준다.💡 논문 핵심 해설 (Deep Analysis)
선형화된 공간에서는 전통적인 선형 제어 설계 기법—예를 들어 LQR이나 H∞—을 바로 적용할 수 있어, 레퍼런스 궤적 분포를 추적하는 최적 제어 입력을 손쉽게 구한다. 이때 레퍼런스가 확률적 분포라는 점은 실제 로봇이나 물리 시뮬레이션에서 발생하는 외란 및 초기 상태 불확실성을 자연스럽게 반영한다는 장점을 제공한다.
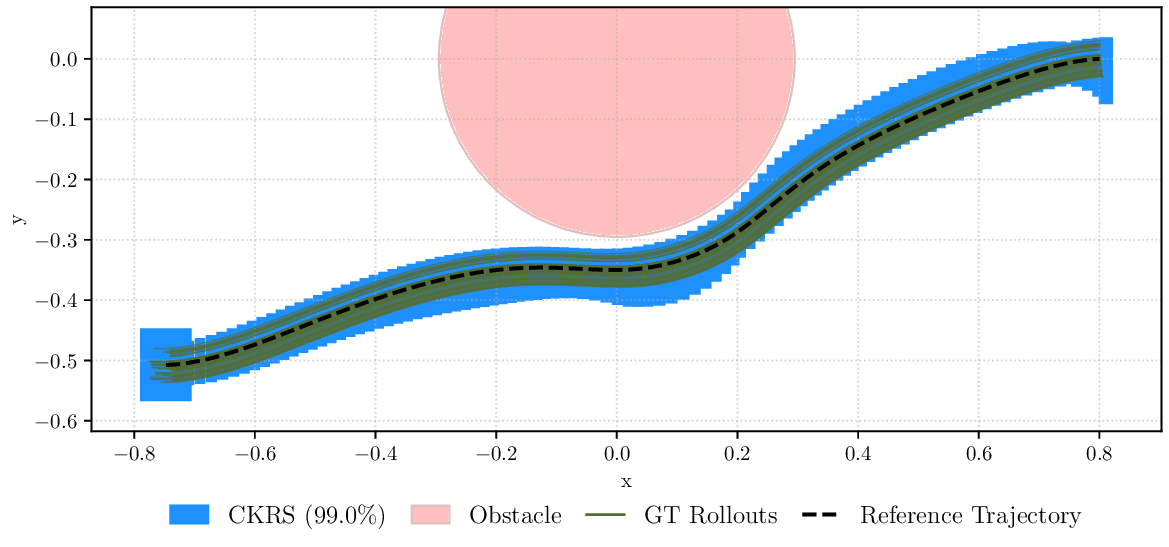
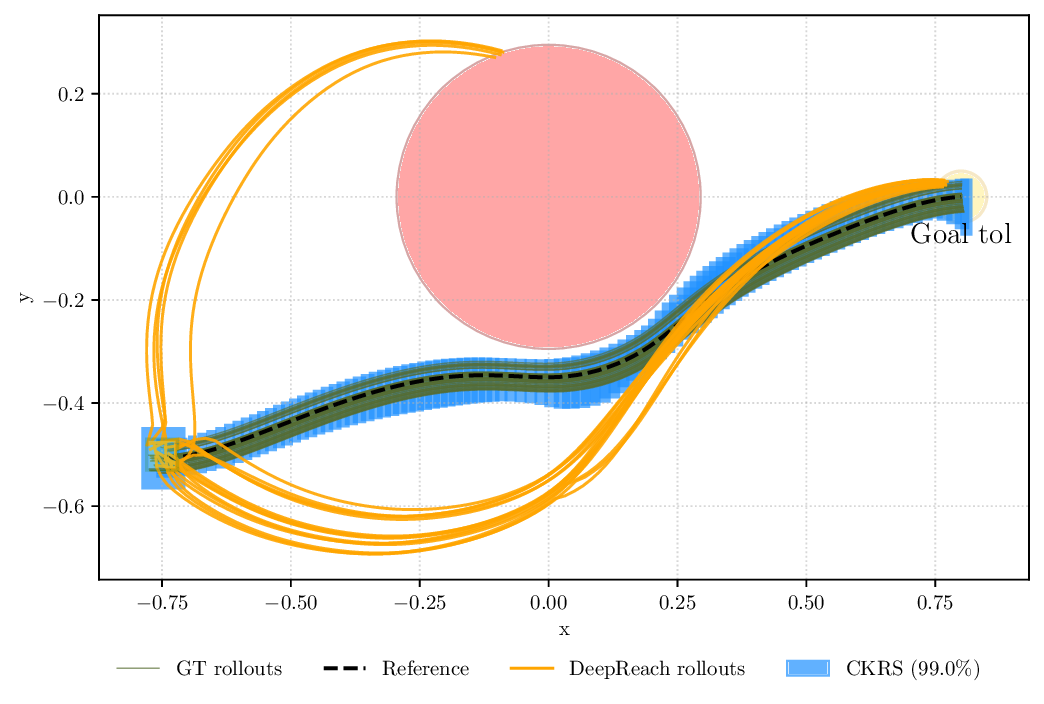
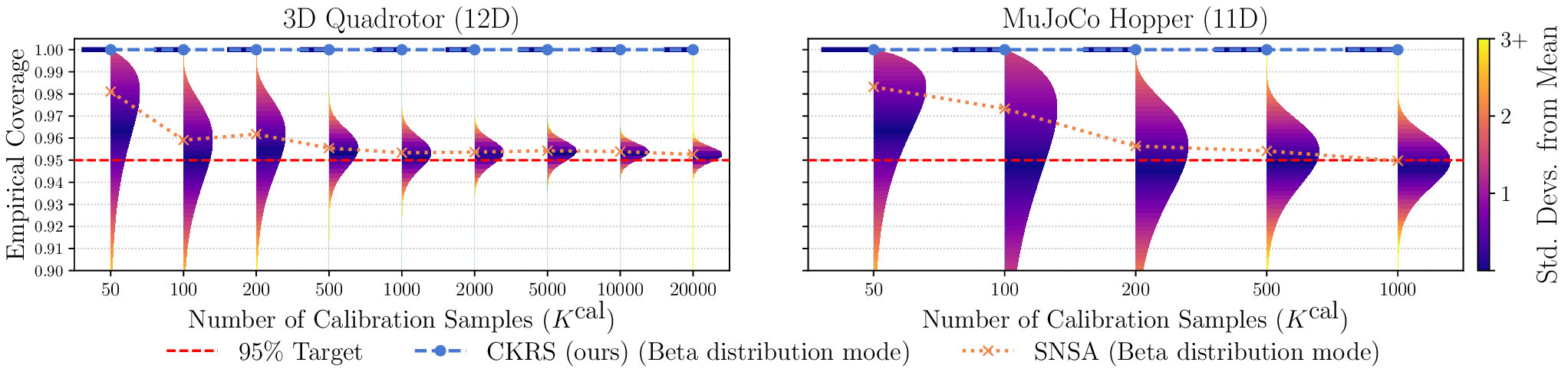
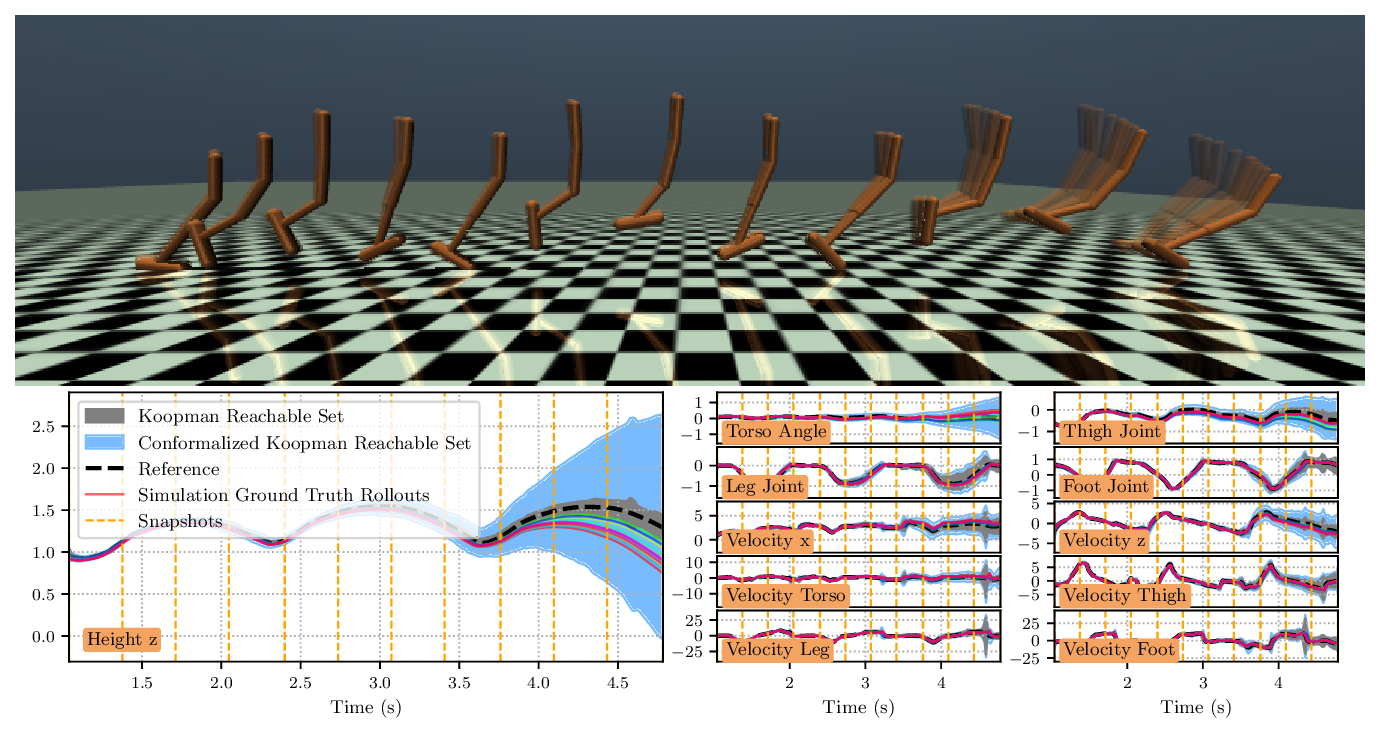
도달 가능 집합을 계산할 때는 선형 시스템의 특성을 이용해 다각형(또는 다면체) 형태로 빠르게 전파한다. 그러나 쿠프만 모델과 실제 시스템 사이에는 불가피하게 모델링 오차가 존재한다. 이 논문은 이러한 오차를 정량화하기 위해 최신 통계 학습 기법인 컨포멀 예측(conformal prediction)을 도입한다. 컨포멀 예측은 데이터에 대한 비정형적 분포 가정을 최소화하면서, 사전 정의된 신뢰 수준(예: 95%)에 대해 유효한 오류 구간을 제공한다. 따라서 도달 가능 집합에 이 오류 구간을 팽창시키면, 지정된 확률로 실제 시스템 궤적이 포함된다는 통계적 보장을 얻을 수 있다. 특히, 한 번 계산된 오류 구간이 레퍼런스 궤적 전반에 걸쳐 재사용 가능하다는 점은 실시간 혹은 반복적인 검증 작업에서 계산 비용을 크게 절감한다는 의미이다.
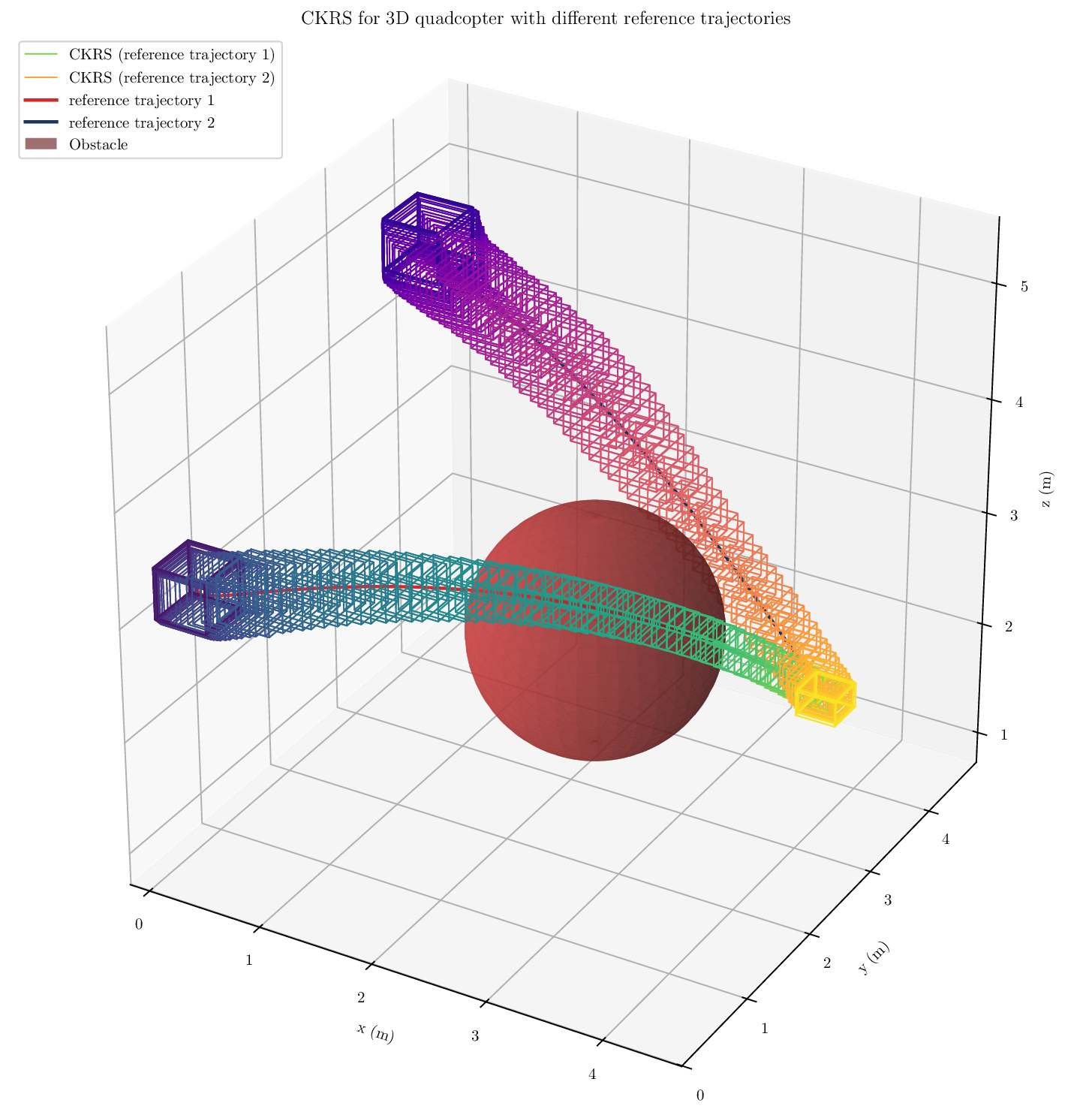
실험에서는 11차원 Hopper, 28차원 Swimmer, 12차원 쿼드콥터 등 고차원 연속 제어 문제에 적용해 기존 방법(예: 샘플 기반 시뮬레이션, 비선형 세트 연산) 대비 도달 가능성 커버리지 비율이 현저히 높고, 계산 시간은 수십 배 가량 단축되었음을 보고한다. 특히, 보수성 측면에서 과도하게 큰 안전 마진을 부여하지 않으면서도 높은 커버리지를 달성한 점은 실용적인 안전 검증에 큰 의미가 있다.
하지만 몇 가지 한계도 존재한다. 첫째, 리프팅 함수 학습에 필요한 데이터 양이 충분히 풍부해야 한다는 전제가 있다. 데이터가 부족하거나 편향될 경우 쿠프만 모델 자체가 부정확해져 전체 프레임워크의 신뢰성이 저하될 수 있다. 둘째, 컨포멀 예측 구간은 데이터의 독립성 가정을 필요로 하는데, 시간 연속적인 시스템 데이터에서는 이 가정이 완벽히 만족되지 않을 가능성이 있다. 셋째, 현재 구현은 오프라인 학습과 오프라인 검증에 초점을 맞추고 있어, 급격히 변하는 환경에서의 온라인 적응성은 추가 연구가 필요하다.
향후 연구 방향으로는 (1) 적응형 리프팅 함수 학습을 통해 온라인 데이터 스트림에 대응하는 방법, (2) 비독립성 데이터를 고려한 확장된 컨포멀 프레임워크, (3) 다중 로봇 혹은 협동 시스템에 대한 확장성을 탐색하는 것이 제시된다. 전반적으로 본 논문은 쿠프만 이론과 최신 머신러닝·통계 기법을 융합해 고차원 비선형 시스템의 안전 검증을 실시간에 가깝게 수행할 수 있는 새로운 패러다임을 제시한다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리