서론

모든 인간의 의사소통은 언어 자체보다 훨씬 더 풍부한 공간에서 시작된다. 말하는 사람이 단 한 마디도 발하지 않기 전에, 기억, 감정, 목표, 유사성, 미완의 주장 등이 구성되는 고차원적이고 언어 이전의 매니폴드가 존재한다. 이 무한히 많은 가능성이 있는 의미의 구름에서, 실제로 생산되는 것은 단 하나의 선형적인 단어 시퀀스다. 같은 내부 상태는 “나는 피곤하다,” “거의 잠을 못잤다,” “오늘은 머리가 멍하다” 등 무한히 많은 변형으로 표현될 수 있지만, 정확히 한 가지 발화만이 이 특정 순간에 결정된다.

우리는 이러한 불가역적인 축소를 *의도 붕괴(intention collapse)*라고 부른다: 인공적이든 생물학적이든 인지 시스템이 방대하고 암시적인 의미 구성에서 단일한 구체적인 언어 메시지로 압축되는 과정. 의도 붕괴는 언어 생성의 주변적 부산물이 아니라, 풍부한 내부 상태를 이산적이고 연속적인 표면에 고착시키는 어떤 시스템에도 필수적인 구조적 특징이다.

현대의 대형 언어 모델(LLMs)은 유사한 패턴을 보여준다. 다음 토큰 예측이라는 친숙한 형식 아래에는 두 단계 계산이 숨겨져 있다: 첫째, 모델은 입력과 매개변수 및 컨텍스트를 통합하여 고차원의 내부 표현을 형성하고; 둘째, 이 표현은 이산적인 토큰 시퀀스로 투영된다. 우리는 이를 의도 상태 $`I`$—첫 번째 토큰이 방출되기 직전에 조건화된 잠재적 표현—and 붕괴 연산자 $`\kappa_\theta`$라고 정의한다, 이는 $`I`$를 언어로 매핑하는 과정이다. 이 매핑은 다대일이며 본질적으로 손실이 있는 과정이다: $`I`$에 포함된 정보가 출력으로 투영될 때 상실될 수 있다.

이 프레임워크는 다양한 추론 강화 기법에 대한 통합적인 관점을 제공한다. 체인 오브 씽크 프롬프팅, 자가 학습 추론, 시간당 훈련 모델, 시험시간 훈련, 그리고 자기 정교화 방법들은 모델이 “생성의 가장자리"에 무엇을 가져오는지, 즉 붕괴 전의 $`I`$의 정보적이고 기하학적인 속성을 어떻게 변화시키는지를 개입하는 것으로 볼 수 있다. $`I`$를 명시적으로 만드는 것은 단순히 방법이 벤치마크 점수를 향상시키는지뿐만 아니라 어떻게 붕괴 전 상태를 재구성하고 그러한 재구성이 성능에 어떻게 영향을 미치는지를 묻게 한다.

이 프레임워크를 구현하기 위해, 우리는 세 가지 간단하고 모델agnostic 의도 지표를 제안한다:

• 의도 엔트로피 $`H_{\text{int}}(I)`$: 붕괴 직전 시점에서 다음 토큰 분포의 샤논 엔트로피, 즉 모델의 즉시 이어짐이 얼마나 집중적이거나 확산되었는지를 측정한다.

• 효과적 차원성 $`d_{\text{eff}}(I)`$: 붕괴 직전 숨겨진 상태에 대한 PCA 고유값 참여 비율, 의도 표현의 기하학적 풍부성을 포착하는 지표이다.

• 잠재적 정보 복구 가능성 $`\text{Recov}(I; Z)`$: $`I`$를 학습하여 작업 결과(예: 정답 여부)를 예측하는 선형 탐색자의 성능, 즉 붕괴 직전에 존재하나 최종 출력에서는 표현되지 않을 수 있는 정보의 양을 측정한다.

이 지표들은 계산 비용이 적게 들며, 아키텍처 수정 없이 적용 가능하며 모든 트랜스포머 기반 모델에 적용할 수 있다.

실증적 기여

우리는 의도 붕괴 프레임워크를 다음을 포함하는 체계적인 실험 연구로 구현한다:

• 세 가지 모델 패밀리: Mistral-7B-Instruct, Llama-3.1-8B-Instruct, 그리고 Qwen-2.5-7B-Instruct, 다양한 지시어 조정된 모델 패밀리를 포함한다.

• 세 가지 추론 벤치마크: GSM8K (자유응답 초등학교 수학), ARC-Challenge (다중 선택 추상적 추론), 그리고 AQUA-RAT (다중 선택 수학 문제), 응답 형식과 문제 구조를 대비하기 위해 선택되었다.

• 세 가지 추론 방식: 직접 답변 기준, 체인 오브 씽크(CoT), 및 빈말 제어(verbosity confounds).

이 $`3\times3`$ 행렬에서 우리는 의도 붕괴 관점을 더욱 구체화하는 다양한 효과를 발견한다:

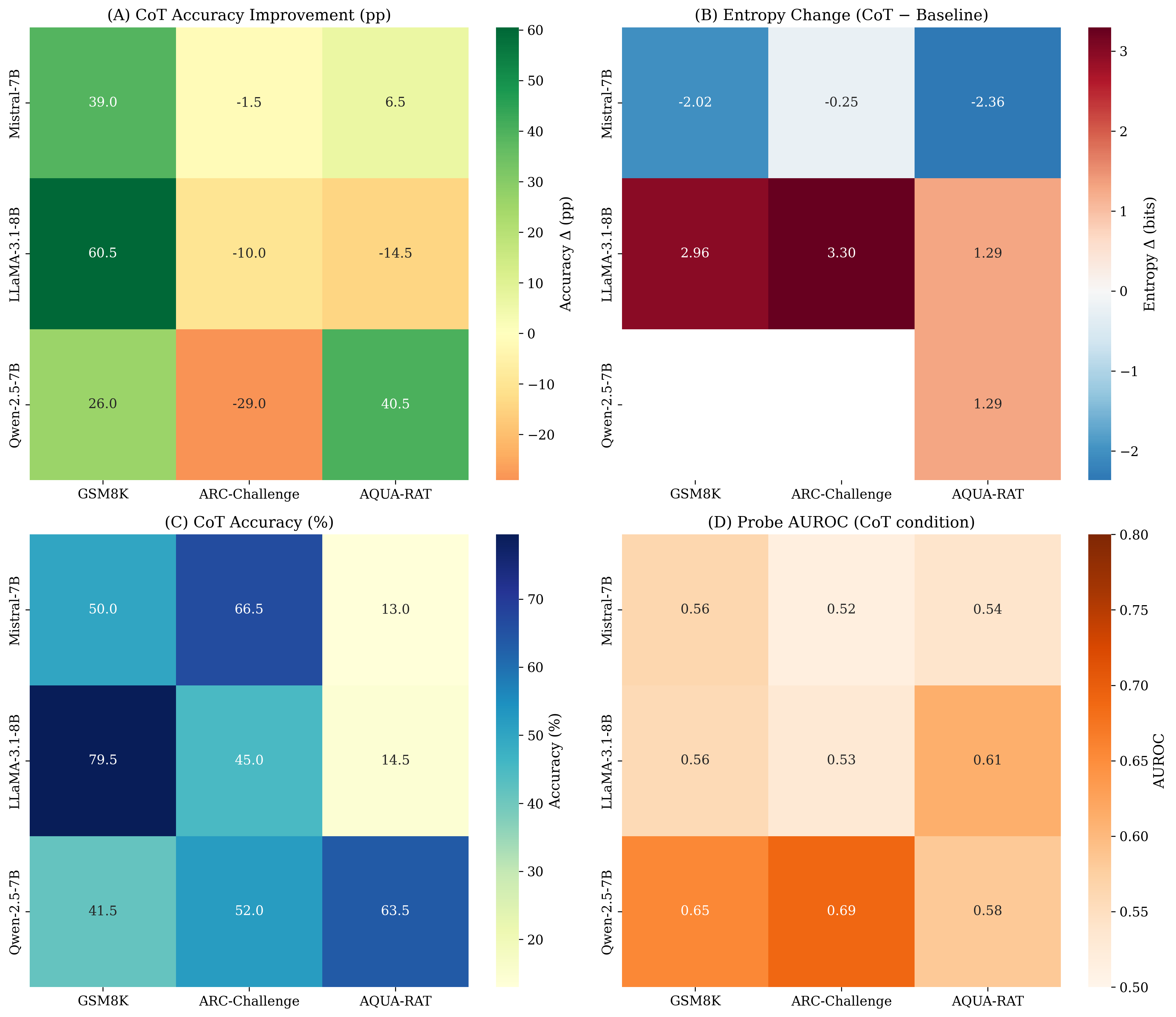
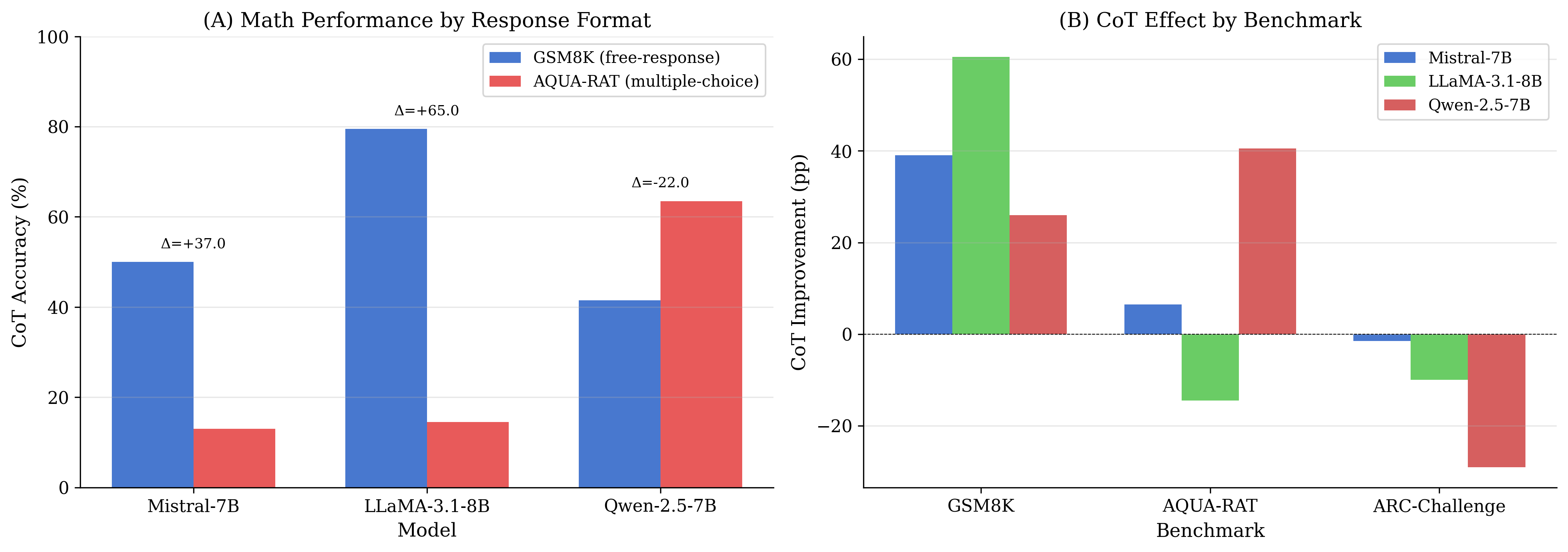
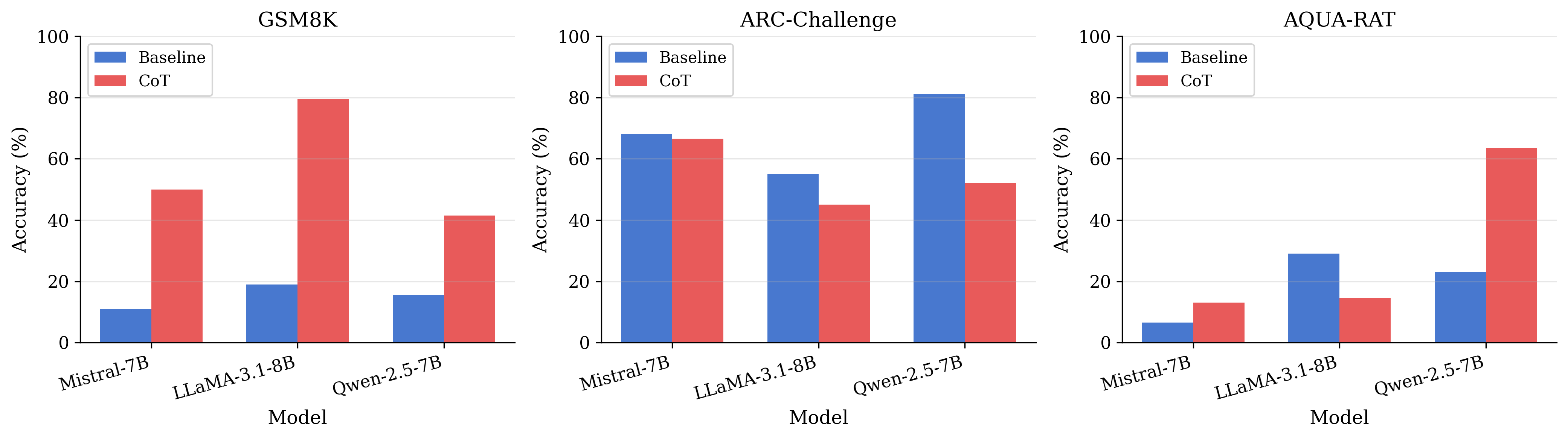
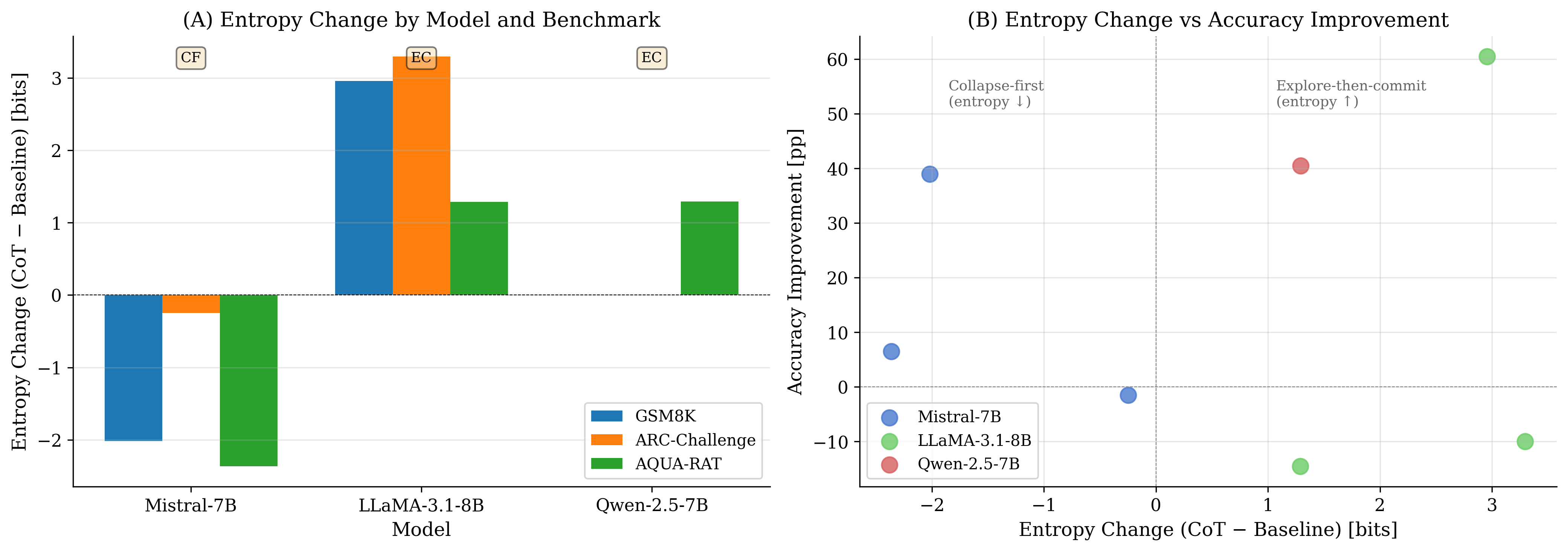
• CoT은 전적으로 유익하지 않다. CoT은 모든 세 모델에 걸쳐 GSM8K에서 큰 성능 향상을 보이지만, ARC-Challenge에서는 일관되게 성능을 저하시키며 AQUA-RAT에서는 혼합된 결과를 내놓는다(특정 모델에 대한 강력한 개선과 다른 모델에 대한 상당한 하락 포함). 이는 최종 이산적 결단의 신뢰성을 변경하는 것에서 내부 상태 변화를 분리하도록 동기화한다.

• CoT은 모델 간 서로 다른 내부 엔트로피 구간을 유발한다. CoT과 기준을 비교한 $`\Delta H = H_{\text{int}}(\text{CoT}) - H_{\text{int}}(\text{Base})`$를 통해, 우리는 질적으로 다른 구간을 관찰한다: Mistral은 CoT에서 더 낮은 붕괴 직전 엔트로피($`\Delta H<0`$) 아래서 작동하고 LLaMA는 CoT에서 더 높은 붕괴 직전 엔트로피($`\Delta H>0`$) 아래서 작동한다. 이러한 레이블은 CoT 대비 기준의 비교적 불확실성을 묘사하며 토큰 수준 시간 동태를 가정하지 않는다.

• 응답 형식은 주요 변인이다. 같은 도메인 내에서 자유 응답과 다중 선택 설정 사이(예: GSM8K의 수학 vs AQUA-RAT의 수학)에 큰 간격이 있음을 나타내며, 형식 선호도가 모델 패밀리 전체에 걸쳐 균일하지 않다는 것을 암시한다.

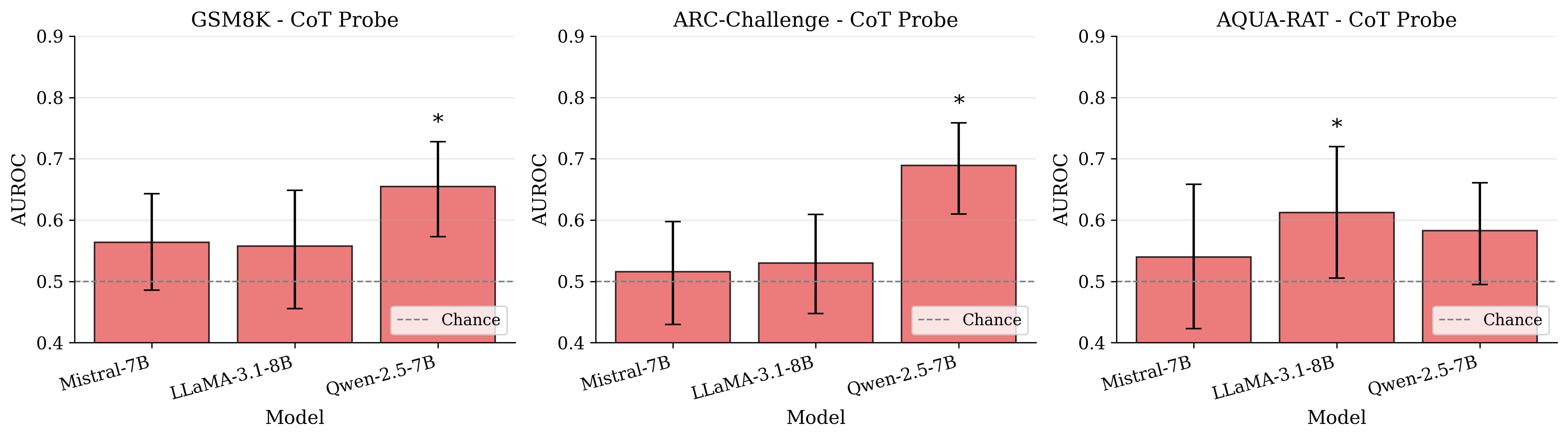
• 복구 신호는 실재하지만 정확도와 분리될 수 있다. $`I`$에서 훈련된 선형 탐색자는 일부 설정에서 AUROC이 기대치를 초과하며, 다중 선택 형식에서 높은 AUROC가 CoT 정확도 저하와 동시에 발생할 수 있다는 사실을 암시한다. 즉, 정보적인 내부 신호가 특정 형식 아래에서는 최종 결정으로 안정적으로 변환되지 않을 수 있다.

• 빈말은 길이 효과를 분리하는데 도움을 주지만 CoT의 특징을 재현하지는 않는다. 긴 출력을 생성하더라도, 빈말은 CoT에서 관찰된 동일한 지표–성능 관계를 체계적으로 재현하지 않아, CoT이 단순히 출력 길이 이상을 변화시킨다는 시각을 지원한다.

또한 중요한 제한 사항도 보고한다. $`H_{\text{int}}(I)`$의 항목별 예측력은 여러 설정에서 약하며; 탐색자의 성능은 층, 작업 및 모델 간에 변화하며; 의도 지표와 하류 정확성 사이의 관계는 인과관계가 아니라 상관관계이다. 또한 CoT은 기준 대비 출력 길이를 크게 증가시키므로, 정확도 향상을 해석할 때 연산 비용 혼란을 고려해야 한다.

개념적 기여

실증 결과를 넘어서, 우리는 의도 붕괴가 LLM 행동에 대해 생각하는 데 유용한 용어장을 제공한다는 주장한다:

• 다양한 추론 시 방법들을 공통의 대상($`I`$)에 대한 개입으로 재구성하여 같은 지표로 직접 비교할 수 있다.

• 잠재적 지식 발현, 생성 전 적합성 및 불확실도 추정과 관련된 평행 문헌을 연결하며, 이러한 스레드를 개념적으로 연결하는 다리 역할을 한다.

• 구체적인 연구 방향을 제안하며, $`I`$ 기반 샘플링 온도 조절 정책 및 $`\text{Recov}(I; Z)`$를 사용한 조기 종료 전략 등이 포함된다.

우리는 LLM들이 의식적 또는 현상학적 의미에서 “의도가 있다"는 것을 주장하지 않는다. 대신, 생물학적이고 인공적인 시스템 모두 복잡하고 풍부한 내부 동적을 가진 다음 이를 급격히 축소된 언어 표면으로 압축하는 공유 계산 모양을 갖는다고 주장한다. 의도 붕괴는 이 구조적 유사성을 포착하되, 인간 인지와 신경망 계산 간의 많은 실질적인 차이를 지우지 않는다. 의도 붕괴의 개념은 모달에 무관하며 텍스트뿐만 아니라 이미지 또는 다중모달 입력에도 적용된다; 여기서는 텍스트만을 벤치마크로 사용하고 미래 연구에서 다중모달 검증을 진행할 예정이다.

구성

제2장에서는 의도 붕괴를 정확한 정의와 추출 프로토콜을 통해 측정 가능한 것으로 구현한다. 제3장은 우리의 프레임워크를 현대의 추론 기법과 연결시킨다. 제4장은 실험 연구를 보여준다. 제5장에서는 관련 작업을 논의하고, 제6장은 한계를 다루며, 제7장은 미래 연구 방향에 대해 결론짓는다.

의도 붕괴 구현화

의도 붕괴를 메타포에서 측정 가능한 것으로 전환하기 위해 필요한 것은 (i) transformer 기반 LLMs에서의 붕괴 직전의 의도 상태 $`I`$의 정확한 정의, (ii) 재생산 가능한 추출 포인트, 그리고 (iii) $`I`$ 내부의 불확실성, 기하학적 특징 및 복구 가능 태스크 관련 신호를 측정하는 지표들이다. 우리는 이 정의들을 모델(Mistral-7B-Instruct, Llama-3.1-8B-Instruct, Qwen-2.5-7B-Instruct)과 벤치마크(GSM8K, ARC-Challenge, AQUA-RAT)를 가로지르는 통제된 $`3\times 3`$ 실험 설계에서 구현하고, 세 가지 추론 방식(Baseline, CoT, Babble)을 사용하며 각 모델–벤치마크 셀당 $`n=200`$ 개의 항목을 포함한다. 전체적으로 우리는 $`I`$를 생성 전 객체로 취급한다: 프롬프트 조건화 후에 추출되며 첫 번째 출력 토큰이 선택되기 직전이다.

의도 상태: 정의 및 추출 프로토콜

정의 1 (의도 상태). $`L`$ 층을 가진 transformer 기반 언어 모델에서 프롬프트 $`x_{1:S}`$를 처리할 때, 의도 상태 $`I`$는 첫 번째 디코딩 단계에서 첫 번째 출력 토큰이 선택되기 직전에 숨겨진 표현을 수집한 것이다:

\begin{equation}
I \triangleq \{h^{(\ell)}_{\text{pre}}\}_{\ell \in \mathcal{L}} \in \mathbb{R}^{|\mathcal{L}| \times d},
\end{equation}

여기서 $`h^{(\ell)}_{\text{pre}} \in \mathbb{R}^{d}`$는 층 $`\ell`$에서 프롬프트의 마지막 위치(첫 번째 출력 토큰이 생성될 위치)에 있는 숨겨진 상태이며, $`\mathcal{L} \subseteq \{1,\ldots,L\}`$는 선택된 층들의 부분 집합이다.

추출 프로토콜

$`I`$를 고정되고 잘 정의된 순간에 추출한다:

1. 모델은 완전한 프롬프트 $`x_{1:S}`$(Baseline vs CoT vs Babble 등 조건별 지시어 포함)을 처리한다.

2. 포워드 패스는 모든 층에서 숨겨진 상태를 계산한다.

3. 각 $`\ell \in \mathcal{L}`$에 대해 프롬프트의 마지막 위치에서 $`h^{(\ell)}_{\text{pre}}`$를 기록한다.

붕괴는 모델이 첫 번째 출력 토큰 $`y_1`$(탐욕적 선택 또는 샘플링을 통해)으로 이산적인 선택을 할 때 시작된다.

이 정의는 $`I`$가 엄격하게 붕괴 전임을 보장한다: 프롬프트 조건화 후에 있지만 첫 번째 토큰의 이산적 결단을 내리기 전이다. 모든 실험 방식에서는 동일한 추출 포인트를 사용하여 프롬프트 전략이 생성 시작 직전 상태를 어떻게 형성하는지를 비교할 수 있다.

내부 계산 및 “생각 시간"에 대한 명확화

모델이 첫 번째 토큰을 즉시 발행하더라도, 층 $`1`$에서 층 $`L`$까지 프롬프트에 대해 비중요하지 않은 내부 계산을 수행한다. 우리의 프레임워크에서는 이 계층별 계산이 붕괴 전 처리를 이루며 $`I`$로 귀결된다. 체인 오브 씽크와 같은 프롬핑 전략은 “생각 토큰"을 내부적으로 요구하지 않고도 $`I`$를 재구성할 수 있다: 그들은 단지 프롬프트 조건화를 통해 처음으로 선택되기 이전의 내부 표현을 변화시킬 뿐이다(첫 번째 토큰 이후에 추가로 생성된 추론 토큰은 정의상 붕괴 후이며 관련이 있을 경우 별도로 분석된다).

모달 무관한 포뮬레이션

우리는 이 프레임워크를 단순히 텍스트 작업에서 평가하지만, 정의는 모달에 무관하다: 다중모달 모델에서는 입력을 공동으로 인코딩한 직후에 추출되지만 여전히 첫 번째 생성된 토큰 바로 전이다. 우리는 교차 모달 검증을 미래 작업에 남겨두었다.

의도 지표

우리는 붕괴 직전의 의도 상태를 측정하기 위한 세 가지 보완적인 지표를 제안한다. 모두 계산 비용이 적게 들며 아키텍처 변경 없이 표준 포워드 패스 출력에서 구할 수 있다.

의도 엔트로피 $`H_{\text{int}}(I)`$

정의 2 (의도 엔트로피). 의도 엔트로피는 붕괴 직전 시점에서 다음 토큰 분포의 샤논 엔트로피다:

\begin{equation}
H_{\text{int}}(I) \triangleq H\bigl(p_\theta(y_1 \mid x_{1:S})\bigr)
= -\sum_{v \in \mathcal{V}} p_\theta(y_1 = v \mid x_{1:S}) \log_2 p_\theta(y_1 = v \mid x_{1:S}),
\end{equation}

여기서 $`\mathcal{V}`$는 어휘이다. 더 낮은 엔트로피는 결단 시점에서의 이어짐 분포가 더 집중된 것을 의미한다.

계산

우리는 붕괴 직전 마지막 프롬프트 위치에서 선택하기 전에 $`H_{\text{int}}(I)`$를 로짓으로부터 구하고 엔트로피는 비트 단위(기수 2)로 보고하며 수치적으로 안정적인 log-sum-exp 계산을 사용한다.

범위 및 해석

전반적으로, $`H_{\text{int}}(I)`$는 전체 어휘에 대한 제약 없는 다음 토큰 엔트로피다. 따라서 이는 붕괴 경계에서의 지역 생성 분산을 측정하며 특정 작업에 대한 답변 선택에 대한 불확실성의 교정된 측정치는 아니다. 특히, $`H_{\text{int}}(I)`$는 프롬프트 끝부분의 어휘 및 토크나이징 세부 사항에 민감할 수 있다(e.g., 접미사 또는 구분자). 따라서 우리는 주로 모델의 붕괴 직전 분포가 조건들 간에 더 집중되거나 확산되는지를 캐릭터라이즈하기 위해 $`H_{\text{int}}`$ 변화를 사용한다.

결정 공간과 대응하는 대체 방안 (MCQ)

다중 선택 벤치마크에서는 옵션 토큰(예: $`\{A,B,C,D,E\}`$)에 대한 분포를 제한하고 붕괴 직전 옵션 정규화된 엔트로피와 *로그 마진을 보고하는 더 결정 공간과 대응하는 진단을 사용할 수 있다. 이러한 양은 최초 토큰 경계에서 옵션별 로그 확률을 기록해야 하며, 현재의 체크포인트 형식은 집계된 엔트로피 값을 저장하지만 옵션별 로그 확률을 보고하지 않으므로 이 리비전에서는 옵션 정규화된 엔트로피나 마진을 보고하지 않는다; 대신, $`H_{\text{int}}`$에 대한 주장은 제약 없는 분포 범위 내에서만 유효하며 이러한 로깅을 미래 작업(Sec. 6)으로 포함한다.

효과적 차원성 $`d_{\text{eff}}(I)`$

정의 3 (층별 효과적 차원성). 예제들에 걸친 의도 상태 셋 $`\{I_i\}_{i=1}^N`$에서 층 $`\ell`$의 층별 효과적 차원성은 PCA 고유값 스펙트럼의 참여 비율이다:

\begin{equation}
d_{\text{eff}}^{(\ell)} \triangleq
\frac{\left(\sum_{j=1}^{d} \lambda_{j}^{(\ell)}\right)^2}{
\sum_{j=1}^{d} \left(\lambda_{j}^{(\ell)}\right)^2},
\end{equation}

여기서 $`\{\lambda_{j}^{(\ell)}\}_{j=1}^{d}`$는 층 $`\ell`$에서 숨겨진 상태의 샘플 공분산 행렬의 고유값이다.

PCA 프로토콜

각 층 $`\ell \in \mathcal{L}`$에 대해:

1. 예제들 $`N`$ 개를 거쳐 층 $`\ell`$에서 숨겨진 상태 $`\{h^{(\ell)}_{\text{pre},i}\}_{i=1}^{N}`$을 수집한다.

2. 데이터 행렬 $`X^{(\ell)} \in \mathbb{R}^{N \times d}`$