/>

서론

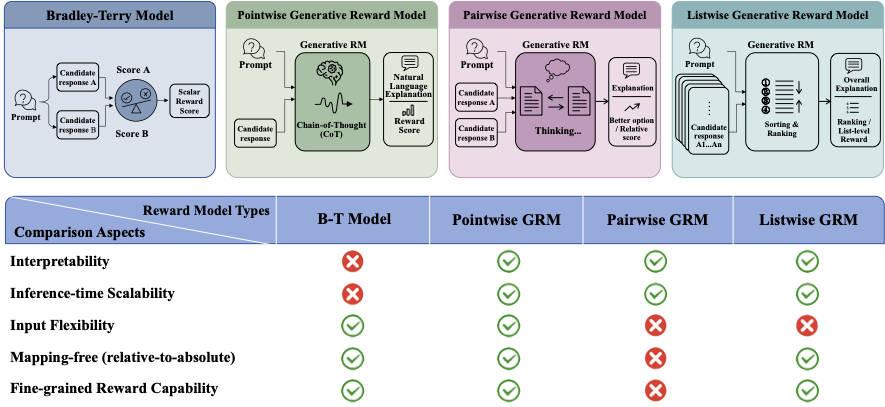
대형 언어 모델(Large Language Models, LLMs)은 다양한 애플리케이션에서 인상적인 성능을 달성했습니다. 그러나 그 행동을 인간의 선호도와 일관되게 맞추는 것은 여전히 중앙 도전 과제입니다. 보상 모델(RMs)은 현대 정렬 파이프라인의 핵심 구성 요소로, 인적 피드백에서 강화학습(Reinforcement Learning from Human Feedback, RLHF)을 위한 훈련 신호를 제공합니다. 명시적인 보상 모델링 접근 방식은 주로 두 가지 유형으로 구분됩니다: 스칼라 보상 모델과 비판 기반 보상 모델입니다. 스칼라 보상 모델은 인간 선호 데이터에 대해 훈련되며, 일반적으로 선택된 응답과 거절된 응답 간의 쌍별 비교 형태로 제공됩니다. 이러한 보상 모델은 일반적으로 값 헤드가 스칼라 점수를 출력하는 LLM을 사용하여 훈련되며, Bradley-Terry(B-T) 모델 기반 목표를 사용합니다. B-T 모델은 우아하고 효과적이지만 여러 실용적인 제한 사항이 있습니다: (i) 해석 가능성의 한계; (ii) 분포 이동에 대한 나쁜 일반화 능력; (iii) 예측을 단일 순방향 패스에서 생성하므로 추론 시간 계산량을 증가시켜 성능 향상을 얻는 잠재력이 제한적입니다.

비판 기반 보상 모델은 종종 LLM-as-a-judge 패러다임으로 구현되며, 자연어 합리화와 연관된 점수를 생성합니다. 이 패러다임은 본질적으로 더 해석 가능하며 추론 시간 확장성을 자연스럽게 지원합니다. 예를 들어 더 많은 계산을 토의나 샘플링 기반 집계에 할당할 수 있습니다. 그럼에도 불구하고, 대부분의 현존하는 LLM 판사 응용 프로그램은 여전히 본질적으로 쌍별로 작동하여 두 개의 응답 중 어느 것이 더 좋은지를 결정하는 데 초점을 맞춥니다. 쌍별 보상 모델을 RL 훈련에 직접 통합하는 것은 중요한 계산 병목 현상을 겪습니다. 이 도전은 표준 평가 프로토콜에서 일어나며, 후보 응답 집합 내의 모든 쌍을 비교해야 합니다. 이 과정은 $`\mathcal{O}(n^2)`$의 시간 복잡도를 가지고 있어 대규모 애플리케이션에 대해 계산적으로 금지되며 효율적인 훈련에 대한 주요 장애물입니다. 게다가 쌍별 판정은 변수 크기 후보 집합에 대한 세밀한, 교정된 보상을 도출하는 데 어려움을 줍니다.

우리는 이상적인 보상 모델이 다음 다섯 가지의 핵심 속성을 충족해야 한다고 주장합니다: (1) 관리 가능한 계산 오버헤드로 RL 훈련 루프에 통합할 수 있는 능력; (2) 크기 조정 가능한 후보 집합에 세밀한, 점별 스코어를 할당하는 능력; (3) 해석 가능한 이유 제공; (4) 분포 이동에 대한 견고성; (5) 추론 시간 확장성을 통해 계산을 향상된 판단으로 교환할 수 있는 잠재력.

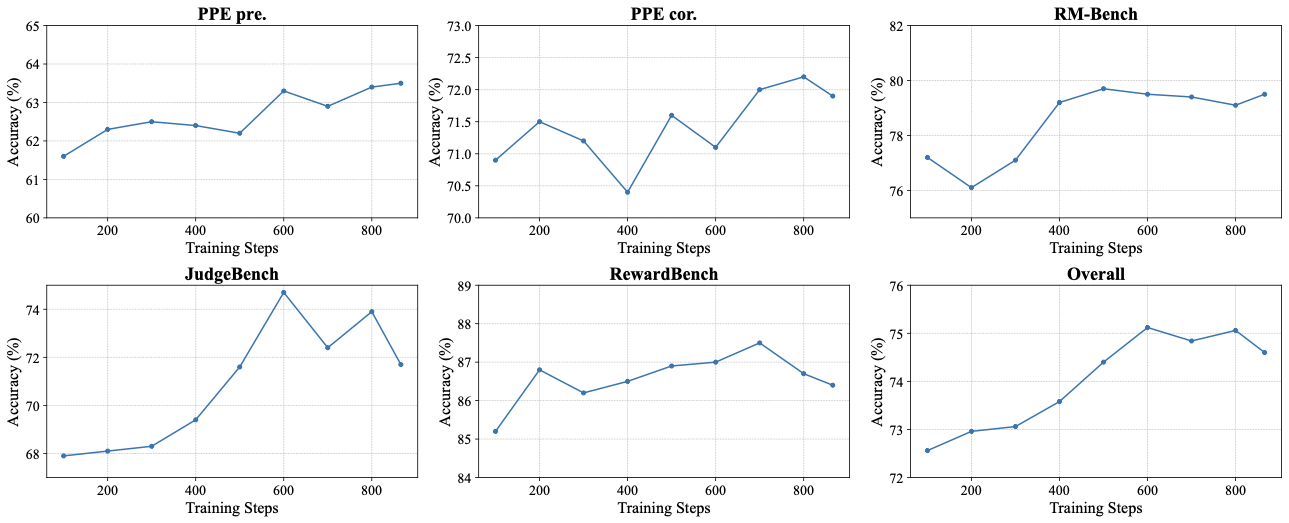
이를 위해, 우리는 Intergroup Relative Preference Optimization (IRPO), 다섯 가지 기준 모두를 충족하도록 설계된 새로운 강화학습 프레임워크를 소개합니다. IRPO는 점별 Generative Reward Models(GRMs)을 훈련하며, Bradley-Terry 스타일의 측정을 유지하면서 임의 수의 후보를 평가할 수 있게 합니다. IRPO는 GRMs으로부터 해석 가능성, 강력한 일반화 능력 및 추론 시간 확장성을 상속합니다. 핵심적으로, IRPO는 RL 훈련 중 선형 시간 복잡도 $`\mathcal{O}(n)`$을 달성하며, 쌍별 방법의 $`\mathcal{O}(n^2)`$ 시간 복잡도와 비교하여 GRMs을 RL 훈련 내에서 배치하는 계산 비용을 크게 줄입니다. 실험 결과는 IRPO가 네 가지 벤치마크에 걸쳐 평균 4.2% 이상 기존 최고 수준(SOTA)의 점별 GRMs보다 우수하다는 것을 보여줍니다. 또한 이 벤치마크 중 일부에서 그 성능은 선두 쌍별 GRMs과 경쟁적이고 접근합니다.

이 작업의 주요 기여 사항은 다음과 같습니다:

• 다섯 가지 핵심 속성을 충족하고 여러 벤치마크에 걸쳐 경쟁적인 성능을 달성하는 IRPO 방법을 소개합니다.
• 체인오브사유(Chain-of-Thought, CoT) 추론을 통한 강화학습으로 GRMs을 개선하기 위한 실용적 전략을 조사하며, CoT 추론이 모델 성능에 결정적인 역할을 한다는 것을 발견합니다.
• 점별 및 쌍별 GRMs을 정책 최적화를 위한 보상 신호로 체계적으로 비교합니다. 우리의 연구 결과는 점별 GRMs이 후속 훈련 단계에서 쌍별 GRMs과 경쟁하거나 우수한 성능을 달성하면서 계산 비용을 크게 줄일 수 있음을 나타냅니다.

관련 작업

Bradley-Terry(B-T) 모델.

선호 데이터 세트가 주어졌을 때,

\begin{equation}
\mathcal{D} = \{ (x^{(i)}, y_c^{(i)}, y_r^{(i)}) \}_{i=1}^N ,
\end{equation}

여기서 $`x`$는 프롬프트, $`y_c`$는 선택된 응답, 그리고 $`y_r`$은 거절된 응답을 나타냅니다. B-T 모델에 따르면 선호 분포는 보상 함수 $`r_{\theta}`$를 사용하여 다음과 같이 정의됩니다:

\begin{equation}
\begin{aligned}
p_{\theta}(y_c \succ y_r \mid x)
&= \frac{\exp\!\big(r_{\theta}(x,y_c)\big)}
{\exp\!\big(r_{\theta}(x,y_c)\big) + \exp\!\big(r_{\theta}(x,y_r)\big)} \\
&= \sigma\!\big(r_{\theta}(x,y_c) - r_{\theta}(x,y_r)\big).
\end{aligned}
\end{equation}

여기서 $`\sigma`$는 로지스틱 함수를 나타냅니다. 이 작업을 이진 분류 문제로 취급하면 음의 로그 우도 목적함수를 얻습니다:

\begin{equation}
\mathcal{L}(r_{\theta})
= -\mathbb{E}_{(x,y)\sim\mathcal{D}}
\!\left[\log \sigma\!\big(r_{\theta}(x,y_c) - r_{\theta}(x,y_r)\big)\right].
\end{equation}

생성적 보상 모델.

인공지능을 인간 선호도와 정렬하는 데 있어 보상 모델(RMs)을 훈련시키는 것은 핵심입니다. 이 분야의 주요 발전 중 하나는 강력한 LLMs를 대규모로 사용하고 정확하게 응답 질을 판단함으로써 AI 기반 피드백 루프의 가능성을 증명하는 것입니다. 후속 연구는 RMs에 대한 더 고급 아키텍처와 훈련 방법론을 탐구했습니다. 예를 들어, Generative Verifiers는 보상 모델링을 다음 토큰 예측 작업으로 재형식화하여 주어진 점수를 정당화하는 설명이나 비판을 생성합니다. 또 다른 중요한 연구 방향은 명시적인 추론 능력을 보상 모델링 과정에 통합하는 것입니다. Critic-RM과 RM-R1 같은 작업들은 RMs에 추론 능력을 부여함으로써 복잡한 작업에 특히 그 평가 정확도를 크게 향상시킬 수 있음을 보였습니다. 또한, RRM은 추론 시간 추론을 확장하는 데 대한 보상 모델 성능의 영향을 조사했습니다. DeepSeek-GRM은 투표 과정을 안내하는 메타 RM을 도입하여 확장 성능을 개선하고 긍정적인 확장 효과를 드러냈습니다. 에이전트 추론을 유인하기 위해 TIR은 외부 도구의 판단을 통합하면 상당한 성능 향상이 가능함을 보였습니다. 우리의 작업과 가장 밀접하게 관련된 것은 J1으로, 이는 최종 쌍별 보상 모델을 개선하기 위한 점별 보조 목표를 갖춘 멀티태스크 학습 프레임워크를 제안합니다. 점별 목표를 포함하더라도 그 훈련 및 평가 파이프라인은 전통적인 쌍별 선호도 설정에 기반하고 있습니다. 대신, 우리는 순수한 점별 강화학습 프레임워크를 제안합니다. 우리의 접근 방식은 대신 그룹 간 평가를 수행하며 두 그룹에 별개의 보상 신호를 할당합니다; 자세한 내용은 [reward-design] 참조.

LLM 정렬을 위한 강화학습

인간 피드백에서의 강화학습(RLHF)은 원하는 행동과 일치하도록 LLMs을 미세 조정하기 위한 표준 기법이 되었습니다. Proximal Policy Optimization(PPO)는 그 안정성과 샘플 효율성으로 인해 대부분의 RLHF 구현에서 핵심 구성 요소였습니다. 초기 응용 프로그램은 이 방법론의 효과성을 입증했습니다. Group Relative Policy Optimization(GRPO)은 추가적인 가치 함수 근사가 필요하지 않으며 동일한 프롬프트에 대한 여러 샘플링 출력의 평균 보상을 기준으로 하는 PPO 변형입니다. 최적화 목표는 기준을 초과하는 출력의 가능성을 증가시키고 부족한 출력은 처벌하는 것입니다; 자세한 내용은 [appendixC] 참조. 최근에는 LLMs에 맞춤화된 강화학습 알고리즘의 개선 사항이 등장했습니다. DeepSeek-R1은 검증 보상과 함께 강화학습을 통해 LLMs의 추론 능력을 크게 향상시켰습니다.

RL 훈련을 위한 쌍별 보상 모델

선호도 기반 보상 모델링의 전통적인 접근 방식은haustive 쌍별 비교를 포함합니다. 이 방법에는 ELO 등급 시스템이 포함되며, 승-패 기록에서 점수를 유도하고 PREF-GRPO는 승률을 보상 신호로 사용합니다. 그러나 이러한 방법들은 계산적으로 요구사항이 높습니다. 그들의 $`\mathcal{O}(n^2)`$ 시간 복잡도가 중요한 병목 현상을 만듭니다. 이 효율성 저하를 해결하기 위해, RRM은 시간 복잡도를 $`\mathcal{O}(n\log(n))`$로 줄이는 쿠오토 토너먼트 전략을 도입합니다. Bootstrapped Relative Policy Optimization(BRPO)은 전체 비교 행렬을 피하고 대신 강화학습 중 임시 참조로서 무작위 샘플링 후보를 사용하여 이득 추정을 수행함으로써 $`\mathcal{O}(n)`$ 복잡도를 달성합니다; 이 접근 방식은 창의적 글쓰기에 대해 실증적으로 효과적이었습니다.

/>

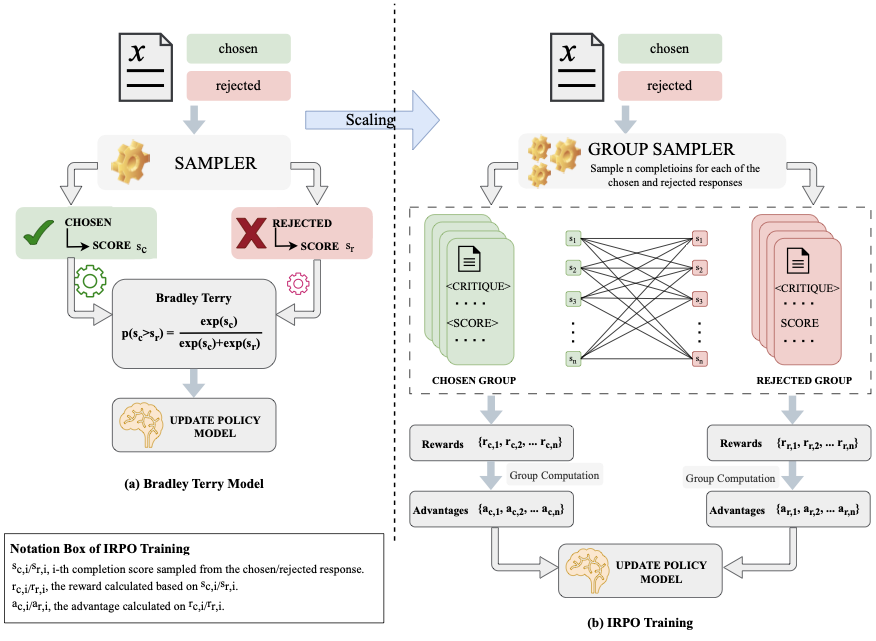
그룹 간 상대 선호도 최적화

IRPO 프레임워크에서는 먼저 응답을 점수화하기 전에 CoT 추론을 생성하여 모델이 추론 시간 계산량을 적응적으로 활용할 수 있도록 합니다. 보상 점수는 다음과 같이 보상 함수 $`r_\theta`$를 사용하여 정의됩니다:

\begin{equation}
r_\theta(s|x,y)=r_\theta(c|x,y) \cdot r_\theta(s|x,y,c),
\end{equation}

여기서 $`x`$는 프롬프트, $`y`$는 응답, $`c`$는 CoT 추론 (예: 기준이나 비판), 그리고 $`s`$는 보상 점수를 나타냅니다. 프롬프트 템플릿은 [appendixA.1] 참조.

기존의 정제된 추론 추적에 의존하는 전통적인 감독 학습 미세 조정과 달리, IRPO는 규칙 기반 보상 설정 하에서 강화학습을 통해 모델이 반복적으로 추론 능력을 정교하게 개선하고 확장하도록 장려합니다.

B-T 모델 확장

우리의 훈련 절차는 점별 생성 학습 프레임워크를 따릅니다. 선호 튜플 $`(x, y_c, y_r)`$이 주어졌을 때, 선택된 응답과 거절된 응답 각각에 대해 보상 점수를 계산하고 모델을 최적화합니다. 구체적으로 [2]에서 설명한 것처럼 B-T 모델은 선택된 응답과 거절된 응답에 대한 점수 샘플링을 통해 학습하며, 그 간격을 늘립니다. GRPO를 기반으로, 우리는 이를 확장하여 각 $`(x,y_c)`$와 $`(x,y_r)`$에 대해 $`G`$ 개의 완성물을 조건부로 샘플링하고 선택된 집합과 거절된 집합을 형성한 후 이 두 집합 간 선호도 강도를 그룹간 보상으로 추정합니다. 구체적으로, 샘플링 후 각 선택된 집합 점수 $`s_i^c`$의 선호도 강도 $`p_i^c`$는 다음과 같이 정의됩니다:

\begin{equation}
    p_i^c = \frac{1}{G}\sum_{j=1}^G \sigma(s_i^c-s_j^r),
\end{equation}

여기서 G는 롤아웃 수를 나타냅니다. 마찬가지로 각 완성 점수 $`s_i^r`$의 선호도 강도 $`p_i^r`$은 다음과 같이 정의됩니다:

\begin{equation}
    p_i^r = \frac{1}{G}\sum_{j=1}^G \sigma(s_i^r-s_j^c).
\end{equation}

우리는 각 샘플의 선호도 강도($`p_i`$)를 그 보상($`r_i`$)으로 취하고, 각 그룹 내에서 이득을 계산한 후 정책 모델을 업데이트합니다. 이를 IRPO의 초기 그룹간 보상 설계로 간주할 수 있습니다.

또한 AUC 지표에 영감을 받아 선호도 강도를 측정하는 대체 방법으로, AUC를 계산합니다:

\begin{equation*}
    r_i^c = \frac{1}{G}\sum_{j=1}^{G} \mathbf{I}(s_i^c > s_j^r),\quad
    r_i^r = \frac{1}{G}\sum_{j=1}^{G} \mathbf{I}(s_i^r < s_j^c).
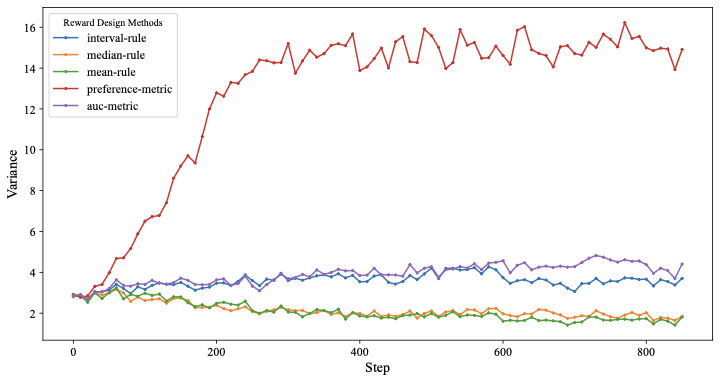
\end{equation*}

보상 설계

선호도 강도를 그룹간 보상으로 사용할 때 문제가 발생합니다. 이 설계에서 선택된 응답과 거절된 응답의 쌍에 대해 선택된 응답의 샘플링 완성 점수가 높아질수록 보상이 증가하고, 마찬가지로 거절된 응답의 점수가 낮아질수록 보상이 증가합니다. 그러나 이는 쌍의 응답 간 본래적인 질 차이가 작을 때 바람직하지 않습니다. 이를 보상 모델의 목표와 상충됩니다. 즉, 일관된 기준 하에서 서로 비교 가능한 점수를 다양한 응답에 할당하는 것입니다. 이 문제를 완화하기 위해 규칙 기반 방법으로 보상 값을 제약합니다:

\begin{equation*}
    r_i^{c} =
    \begin{cases}
    1, & s_i^{c} > \hat{\theta}_r \\
    -1, & \text{otherwise}
    \end{cases},\quad
    r_j^{r} =
    \begin{cases}
    1, & s_j^{r} < \hat{\theta}_c \\
    -1, & \text{otherwise}
    \end{cases}
\end{equation*}

여기서 $`\hat{\theta}`$는 샘플링된 완성 점수 집합에서 계산된 추정값을 나타냅니다. 우리는 다음과 같은 세 가지 추정 방법을 고려합니다.

산술 평균(점추정)

산술 평균은 응답 점수의 간단한 점 추정치를 제공하며 샘플 평균을 계산함으로써 얻습니다:

\begin{equation*}
\hat{\theta} = \frac{1}{G}\sum_{i=1}^{G} s_i
\end{equation*}

중앙값(점추정)

중앙값은 응답 점수의 다른 점 추정치를 제공합니다. 완성 점수는 오름차순으로 정렬됩니다 $`s_1

\begin{equation*}
\hat{\theta} = s_{\lcei
</div>
<div style="margin-top: 20px;"><a href="https://arxiv.org/pdf/2601.00677.pdf" target="_blank">ArXiv 원문 PDF 보기</a></div>
<div class="mobile-ad w-full my-6 text-center" style="border: 2px dashed red; background: #ffe6e6;"><ins class="adsbygoogle" style="display:block" data-ad-client="ca-pub-1873718820012422" data-ad-slot="auto"></ins><script>(adsbygoogle = window.adsbygoogle || []).push({});</script></div>

<br>
<h4>📊 논문 시각자료 (Figures)</h4>

![Figure 1](/posts/2026/01/2026-01-02-190710-irpo__scaling_the_bradley_terry_model_via_reinforc/irpo.drawio.png)

<br>
<br>

![Figure 2](/posts/2026/01/2026-01-02-190710-irpo__scaling_the_bradley_terry_model_via_reinforc/model_var.png)

<br>
<br>

![Figure 3](/posts/2026/01/2026-01-02-190710-irpo__scaling_the_bradley_terry_model_via_reinforc/model_performance_6_benchmarks2.png)

<br>
<br>

![Figure 4](/posts/2026/01/2026-01-02-190710-irpo__scaling_the_bradley_terry_model_via_reinforc/con7.png)

<br>
<br>


<h4 style="margin-top: 3rem; margin-bottom: 1rem; border-bottom: 1px solid #e5e7eb; padding-bottom: 0.5rem;">감사의 말씀</h4>
이 글의 저작권은 연구하신 과학자분들께 있으며, 인류 문명 발전에 공헌해주신 노고에 감사를 드립니다.