맥락

대리적 대형 언어 모델(LLM)은 물류, 관리, 의료, 도시 계획, 교통 등 다양한 분야에서 큰 워크플로우 자동화와 의사결정 지원 시스템의 중요한 요소로 부상하고 있다. 따라서 LLM 에이전트는 스케줄링과 같은 관련 조합 최적화 문제에 대한 알고리즘 개발 도구로 활용되고 있다. 자연어 처리에서 최적화를 위한 연구가 이루어졌으며, 자연어 기반 문제 설명을 가치 있는 수학적 형식으로 효과적으로 변환하였다. 언어 모델 에이전트는 자연어 설명과 수학적 형식을 제공받아 최적화 문제에 대한 알고리즘 해법을 생성하는 데 능숙하며, 시간 제약 상황에서 인간 전문가의 성능을 초월하는 것으로 입증되었다.

연구자와 산업계 모두 이러한 프레임워크에 큰 관심을 보이고 있으며, 이는 LLMs의 주요 응용 분야를 위한 귀중한 벤치마크로서 역할을 한다. 이러한 응용은 LLM 성능의 두 가지 중요한 측면인 자연어 처리(NLP)와 프로그래밍을 자극한다. 그러나 언어 모델 에이전트는 조합 최적화 문제에 적용되어 왔으나, 주로 학술 사례에서만 이루어졌으며, 이러한 문제들은 직접적으로 또는 인간 교육용 텍스트북으로부터 영감을 받은 프레임워크를 사용한다. 이러한 연구는 LLM 에이전트를 위한 구조화된 벤치마크를 제공하지만, 단일 목표에 한정되며 정확한 해법 접근 방식으로 해결할 수 있다.

현실을 반영하는 조합 최적화 문제에 대한 제한적인 작업이 이루어졌다. 현실을 반영하는 문제는 텍스트북에 거의 기록되지 않고 계산 자원의 제약이나 문제의 불확실성 때문에 정확하게 해결하기 어렵다. 게다가, 실제 문제에는 빠짐없이 타협점이 있으며, 실제 의사결정자는 이러한 타협점의 의미를 알아야 한다는 것을 요구한다. 즉, 다목적 최적화 작업에서 발생하는 파레토 프론트의 결과를 이해해야 한다. LLM 에이전트는 정확한 해법자가 해결하기 어려운 문제에 대한 휴리스틱 알고리즘을 개발하는데 적용되었다. 그러나 다목적 최적화 문제에 대한 LLM 에이전트 솔루션은 제한적으로 연구되었다.

논거

본 연구의 주요 관심사는 조합 최적화 문제를 해결하는 언어 모델 프레임워크의 개발이다. 이는 현실 세계에서 발생할 수 있는 최악의 시나리오를 반영한다(여러 벤치마크 연구와 달리, 문제 설정이 이상적인 시나리오인 경우). 조합 최적화 문제는 NP-난해 문제로 인해 종종 해결하기 어렵고, 부분 집합의 조합 폭발로 정확한 해법을 찾기 어려워진다. 또한 실제 문제는 다목적이며 의사결정자는 상충되는 비즈니스 요구사항 등을 직면한다.

정확한 해법자가 해결하기 어려운 문제에 대한 휴리스틱 알고리즘 개발을 위한 에이전트 프레임워크는 이러한 경우에서 귀중한 도구로 사용될 수 있다. 정확한 해법자에게 해결하기 어려운 문제는 메타휴리스틱으로부터 근사해를 찾아야 한다. 또한 다목적 최적화 문제에서는 휴리스틱 해의 결합이 때때로 큰 성능 향상을 가져올 수 있으며, 이러한 해는 더욱 높은 수렴성과 다양성을 가진 비지배 프론트를 형성한다. 예를 들어, 카디널리티 제약 평균-분산 포트폴리오 최적화(CCPO)가 이와 잘 맞는다. 표준 마코위츠 평균-분산 포트폴리오 최적화와 달리 CCPO는 NP-난해 문제이며, 비볼록하고 불연속적인 효율 프론트를 가진다. 메타휴리스틱 CCPO 솔루션에 대한 연구가 광범위하게 이루어졌으며, 결합된 휴리스틱의 성능이 단일 휴리스틱보다 크게 향상된다는 것이 입증되었다.

기여

본 논거에 따라 본 연구는 다음과 같은 몇 가지 발견을 제공한다:

• 이 연구는 NP-난해 다목적 조합 최적화 문제를 해결하는 알고리즘 포트폴리오의 생성에 사용되는 에이전트 언어 모델 프레임워크를 제시한다. 이 에이전트 프레임워크는 알고리즘 포트폴리오 구축과 관련된 막대한 개발 부담을 단순화하며, 새로운 알고리즘의 발견 가능성이라는 추가적인 이점을 제공한다.
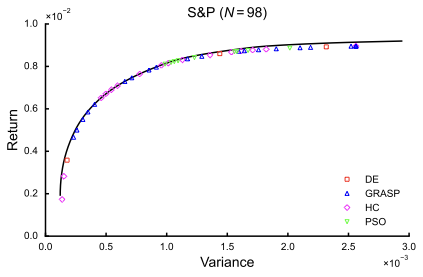
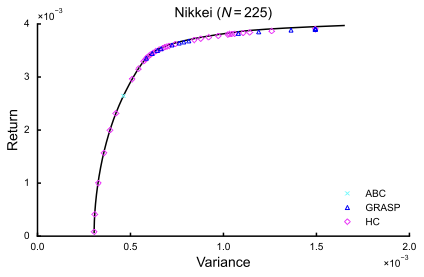
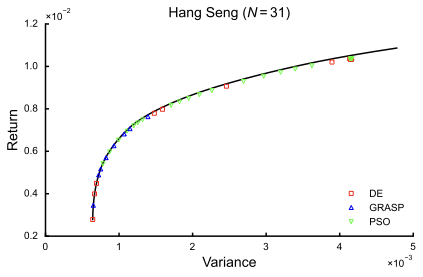
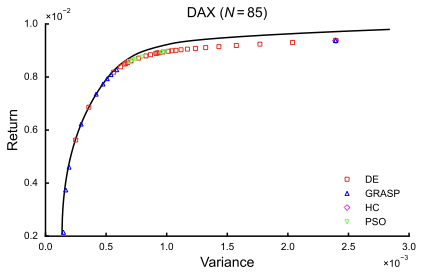
• 본 연구는 여러 학술적으로 광범위하게 연구된 다목적 투자 포트폴리오 최적화 벤치마크 문제에서 에이전트 프레임워크와 생성된 알고리즘 포트폴리오를 검증한다. 이 에이전트 프레임워크는 OR-Library로부터 가져온 CCPO 사례에 대해 현존하는 상태와 비슷한 알고리즘을 생성하고, 그 결과 결합된 알고리즘이 성능을 크게 향상시킨다는 것이 입증되었다.

예비

LLM 에이전트

프로그래밍 에이전트는 컴퓨터 과학과 기계 학습 커뮤니티에서 많은 주목을 받고 있다. 프로그래밍 능력과 복잡한 워크플로우를 단순화하는 데 매우 유망하다는 것이 입증되었다. 또한 조합 최적화 분야에서도 크게 주목받았으며, 불가능하거나 NP-난해 문제를 해결하기 위한 알고리즘 설계 부담이 크기 때문이다. Self-Refine, FunSearch 및 ReEvo와 같은 여러 프로그래밍 에이전트 프레임워크는 성공적으로 조합 최적화 문제를 해결하는 데 사용되었다.

에이전트 프레임워크

본 연구에서 사용된 프로그래밍 에이전트 프레임워크는 알고리즘 포트폴리오 개발의 핵심 요소로 기능한다. 반복적인 에이전트를 이용한 알고리즘 생성 및 발견에 성공적으로 활용되었기 때문에, 본 연구의 프레임워크는 이러한 아키텍처를 기반으로 한다. 언어 모델을 사용하여 한 번만 생성하면 자주 하위 최적 성능이나 실행 오류가 발생하는 것으로 나타났다. 따라서 본 연구에서 사용된 에이전트 프레임워크는 외부 환경과의 반복적인 세밀화에 의존한다.

본 연구에서는 언어 모델을 $`\mathcal{M}`$으로 지칭하며, 이를 코딩 에이전트로 설정하였다. [[IMG_PROTECT_N]]은 코딩 에이전트 $`\mathcal{M}`$을 통해 알고리즘 $`\mathcal{A}`$를 생성하는 과정을 설명한다. 여기서 $`\mathbf{p}`$는 공학적으로 설계된 프롬프트 템플릿 벡터이며, $`a`$, $`f`$, 그리고 $`s`$는 이전 반복에서의 알고리즘, 피드백 및 점수이다.

\begin{align}
    \mathcal{M}(\mathbf{p}, a, f, s) \;\mapsto\; \mathcal{A} [[IMG_PROTECT_N]]
\end{align}

본 연구의 에이전트 프레임워크는 Self-Refine을 기반으로 하는, 반복적인 흉내 내기 에이전트 프레임워크에 근거한다. 이 프레임워크는 반복적으로 사용되는 탐욕적 세밀화를 통해 알고리즘을 생성한다. [[IMG_PROTECT_N]]은 본 연구의 에이전트 프레임워크의 추론-액션 반복을 설명한다. 여기서 추론은 공학적으로 설계된 프롬프트 템플릿 벡터 $`\mathbf{p}=\{p,p_\text{PF},p_\text{RA},p_\text{I/O}\}`$를 포함하며, 이는 각각 일반 반복 지시문($`p`$), 문제 형식화($`p_{\text{PF}}`$), 역할 할당($`p_{\text{RA}}`$) 및 포맷팅 지침($`p_{\text{I/O}}`$)을 나타낸다. 또한 $`a_t^*`$, $`f_t^*`$, 그리고 $`s_t^*`$는 각각 반복 $`t`$에서 가장 좋은 점수를 받은 이전 반복의 알고리즘, 피드백 및 점수이며, 적절한 위치에 프롬프트 템플릿에 주입된다. 액션은 문제 매개변수 및 입력($`x`$, 반복을 통해 일정함)과 생성된 알고리즘 $`\mathcal{A}`$를 요구한다.

\begin{align}
    \mathcal{A}_{t} \sim \mathcal{M}(\mathbf{p}, a_{t-1}^*, f_{t-1}^*, s_{t-1}^*) \quad \& \quad \{f_{t},s_{t}\}\sim\mathcal{A}_{t}(x) [[IMG_PROTECT_N]]
\end{align}

점수

본 연구에서는 알고리즘 해법이 언어 모델 에이전트 $`\mathcal{M}`$ 외부에서 평가되며, 환상적인 자기평가를 방지한다. 생성된 알고리즘 $`\mathcal{A}`$는 다목적 조합 최적화 문제에 대한 메타휴리스틱 해법을 제공해야 한다. 따라서 추론-액션 반복의 액션 부분은 간단한 목적 함수 적합도 점수를 넘어서 더 많은 지표를 요구한다. 여기서 다목적 최적화 문제를 연구하는 의사결정자는 솔루션의 효율 프론트, 즉 가장 가까운 근사해 집합에 대한 정보를 필요로 한다. 예를 들어, 투자 포트폴리오 최적화에서 합리적인 의사결정자는 위험이 더 크고 동일한 수익률을 가진 자산 포트폴리오를 선택하지 않을 것이다. 반대로 그들은 위험이 같지만 수익률이 낮은 포트폴리오도 선택하지 않을 것이다. 본 연구에서는 효율 프론트, 또는 형식적으로는 파레토 프론트를 솔루션 집합 $`Y`$에서 엄격히 비지배 해의 부분집합 $`H \subseteq Y`$로 정의한다. [[IMG_PROTECT_N]]은 점 $`y' \in Y`$가 다른 점 $`y \in Y`$를 목적 함수 차원 $`n`$에서 엄격히 지배하는 것을 정의하며, [[IMG_PROTECT_N]]은 엄격히 비지배 해의 부분집합 $`H`$를 정의한다.

\begin{align}
 y' \prec y \;\Longleftrightarrow\; y'_i < y_i \quad \forall i \in \{1,\dots,m\} [[IMG_PROTECT_N]] \\
 H = \{ y \in Y \mid \forall y' \in Y,\; y' \not\prec y \} [[IMG_PROTECT_N]]
\end{align}

생성된 해집합 $`H`$의 성능을 측정하기 위해 여러 성능 지표가 사용될 수 있다. 효율 프론트 성능은 주로 수렴성과 커버리지/다양성을 통해 측정된다. 수렴성은 근사해 프론트와 이론적 파레토 최적 프론트 간의 가까움을 나타낸다. 커버리지는 효율 프론트를 따라 얻어진 근사해의 분포 균일성을 나타낸다. 또한 도메인에 특화된 지표를 사용하여 파레토 프론트 성능을 측정할 수 있다. 예를 들어, 퍼센티지-오차(PERCENTAGE-DEVIATION ERROR)는 CCPO의 수렴성 성능을 벤치마킹하는 데 일반적으로 사용된다. 그러나 본 연구에서는 수렴성과 커버리지를 측정하는 하이브리드 지표에 의존한다. 이러한 효과를 위해 히퍼볼륨 지시자와 역 생성 거리(IGD)가 일반적으로 사용되며, 본 연구에서는 IGD를 표준 마코위츠 포트폴리오 최적화의 제약 없는 효율 프론트(UEF)를 점수 매기기 위한 참조로 활용한다. [[IMG_PROTECT_N]]은 IGD 지표의 계산을 설명하며, 여기서 $`P`$는 본 연구에서 UEF로 취급되며 이론적 최적 파레토 해 $`y^*`$ 집합을 나타내고, $`H`$는 비지배 근사 파레토 해 $`y`$ 집합이며, $`\| y^* - y \|`$는 근사해 $`y`$와 가장 가까운 최적해 $`y^*`$ 간의 유클리드 거리를 나타낸다.

\begin{align}
\text{IGD}(P, H) = \frac{1}{\text{card}(P)} \sum_{y^* \in P} \min_{y \in H} \| y^* - y \| [[IMG_PROTECT_N]]
\end{align}

문제 형식화

본 연구는 문헌에서 광범위하게 연구된 카디널리티 제약 평균-분산 포트폴리오 최적화(CCPO) 문제를 사용하며, 여기서 현존하는 알고리즘 성능을 참조로 맵핑할 수 있다. CCPO는 표준 마코위츠 평균-분산 포트폴리오 최적화의 제약된 버전이다. 표준 마코위츠 접근법과 마찬가지로 분산은 투자 포트폴리오와 관련된 위험을 충분히 측정하는 것으로 가정된다.

목표

CCPO는 다목적 최적화 문제로 표현될 수 있으며, 목적은 $`N`$ 자산의 우주에서 구성 가능한 잠재적인 포트폴리오에 대해 포트폴리오 위험을 최소화하고 포트폴리오 수익률을 최대화하는 것이다. 표준 마코위츠 접근법과 동일하게 [[IMG_PROTECT_N]]은 위험을 정의하며, 여기서 $`w_i`$는 자산 $`i`$($`\forall i \in \{1,\ldots,N\}`$)에 대한 보유 비율이고, $`\sigma_{ij}`$는 자산 $`i`$와 $`j`$($`\forall i \in \{1,\ldots,N\}`$ 및 $`\forall j \in \{1,\ldots,N\}`$) 간의 공분산이다. 수익률은 [[IMG_PROTECT_N]]에 따라 단순히 자산 $`i`$($`\forall i \in \{1,\ldots,N\}`$)의 기대 수익률 $`\mu_i`$의 가중 합이다.

\begin{align}
    \min \quad &\sum_{i=1}^{N} \sum_{j=1}^{N} w_i w_j \sigma_{ij} [[IMG_PROTECT_N]] \\
    \min \quad &-\sum_{i=1}^{N} w_i \mu_i [[IMG_PROTECT_N]]
\end{align}

위의 CCPO 문제의 계산 복잡성으로 인해 단일 목적 함수로 변환하는 것이 바람직하며, 이는 단일 목표 메타휴리스틱을 사용할 수 있게 한다. 다목적 메타휴리스틱은 이미 도전적인 문제에 추가적인 계산 부담을 가한다. 따라서 여러 목표를 단일 목표로 변환하기 위한 기법이 필요하며, 여기서는 $`\varepsilon`$-제약 조건 목적 함수 대신 선형 스칼라화를 위해 가중합(WS) 방법을 사용한다. $`\varepsilon`$-제약 조건 목적 함수와 달리 WS 목적 함수는 효율 프론트의 비볼록 영역을 커버하지 않으며, 그 성질상 오직 목적 집합의 볼록 껍데기에 속한 해점을 찾을 수 있다. 그러나 CCPO 효율 프론트에 관심 있는 의사결정자는 정확한 프론트 모양보다는 이를 제공하는 타협 정보에 만족한다. 따라서 본 연구에서는 계산 효율성을 위해 WS를 사용하며, 비볼록 영역은 고려하지 않는다. 다목적 최적화 문제에서 완전한 프론트 다양성과 커버리지를 요구하는 경우 $`\varepsilon`$-제약 조건 목적 함수를 선택해야 한다.

여기서 위험 및 수익률 목표 사이에 사전 선호도는 없다. 이 연구에서는 투자 포트폴리오 솔루션의 효율 프론트에 관심이 있다. 따라서 WS 방법의 선형 가중치를 스캔하여 효율 프론트를 찾을 필요가 있으며, 메타휴리스틱만으로 효율 프론트를 커버할 수 없다는 가정은 합리적이지 않다. 일반적인 $`n`$ 개의 목표에 대해 가중 벡터 $`\boldsymbol{\lambda}`$는 무게 단위 단체를 탐색하여 찾을 수 있다. 타협 비율을 스캔하는 것은 단순히 무게 단체 $`\Lambda^{n-1}`$를 스캔하는 것으로 정의된다.

\begin{align}
    \min \quad &\sum_{i=1}^{N} w_i \mu_i \\
    s.t. \quad &\sum_{i=1}^{N} w_i^2 = 1, \; w_i \geq 0 \label{risk}\\
    \min \quad &-\sum_{i=1}^{N} w_i \mu_i \label{return}
\end{align}