영향력 최대화(IM) 문제는 소셜 네트워크 분석에서 중요한 과제로, 네트워크 내의 영향력 있는 노드(시드 사용자)를 식별하여 그들의 활성화가 영향력 확산을 최대로 하는 방식입니다. 이 문제는 바이럴 마케팅, 소셜 네트워크 분석, 루머 제어, 공중 보건 캠페인 등 다양한 도메인에서 중요하며, 네트워크 동역학 이해와 활용이 필수적입니다. 기업들은 단순히 말하기 마케팅을 통해 제품을 홍보하고자 하며, 정책 입안자는 최소 자원으로 인식 캠페인의 도달 범위를 최대화하려고 합니다. 영향력 최대화는 이러한 과정을 최적화하여 가장 효과적인 영향자를 선택하는 데 도움이 됩니다.

IM 문제는 네트워크 지식과 의사결정 과정에 따라 오프라인 및 온라인 설정으로 분류할 수 있습니다. 일부 IM 연구는 전체 네트워크 구조와 영향력 확산 확률을 사전에 알고 있는 오프라인 설정에 초점을 맞추며, 최적의 시드 세트를 사전 계산합니다. 그러나 실제 상황에서는 네트워크가 동적으로 변화하고 실시간으로 영향력이 전파되므로 온라인 설정에서 IM을 연구해야 합니다. 우리의 연구는 네트워크가 변하거나 새로운 정보가 제공되는 경우 의사결정을 적응적으로 하는 온라인 IM 문제에 중점을 둡니다.

문헌 고찰

IM은 다양한 상황에서 광범위하게 연구되어 왔습니다. 다음은 대표적인 작업들을 간략히 조사한 것입니다: 기본적인 IM 프레임워크를 Independent Cascade(IC) 모델과 Linear Threshold(LT) 모델 하에 소개하여 영향력 함수의 submodularity를 증명하고 $`(1-1/e)`$ 근사도를 갖는 그리디 알고리즘을 가능하게 했습니다. Cost-Effective Lazy Forward(CELF) 알고리즘은 submodularity를 활용해 그리디 효율성을 높였으며, CELF++로 더욱 개선되었습니다. Reverse Influence Sampling(RIS)을 사용하여 오프라인 확장성을 개선했지만, 온라인 설정에서는 제한적이었습니다. 최근에는 실행 시간을 더 개선하기 위해 커뮤니티 기반 방법도 탐구되었습니다.

다음으로, Combinatorial Multi-Armed Bandit(CMAB) 접근법은 submodular 보상에 Upper Confidence Bound(UCB), Thompson Sampling 및 관련 전략을 적용하여 반대 피드백 하에서 후회 경계를 설정했습니다. Explore-Then-Commit Greedy는 전체 피드백을 받는 경우 확률적 submodular 보상을 위해 개발되었으며, LT 하에서는 노드를 분할하는 ClusterGreedy를 소개했습니다. Moth-Flame 최적화 알고리즘은 영향자를 식별하고, Combinatorial UCB(CUCB)는 확률적으로 트리거되는 아ーム을 위한 것입니다. 또한 온라인 IM 연구는 동적인 네트워크와 부분 피드백에 초점을 맞추었습니다. 적응적 시드 선택 방법을 제안하였으며, CMAB 프레임워크를 사용하여 피드백이 제한적인 상황에서 탐색과 활용을 균형 있게 유지했습니다. 그러나 계산적으로 집약적이었습니다.

기여

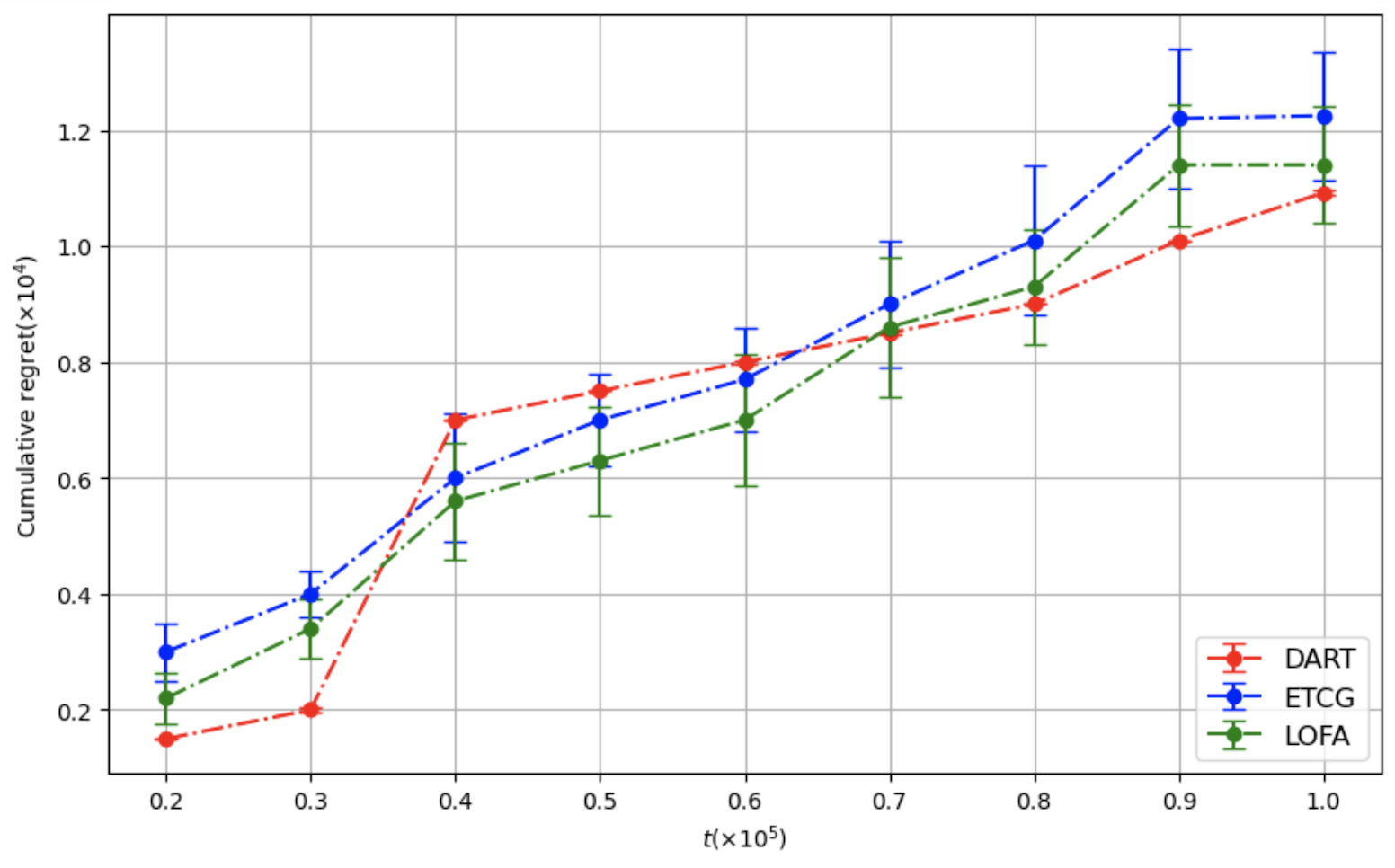
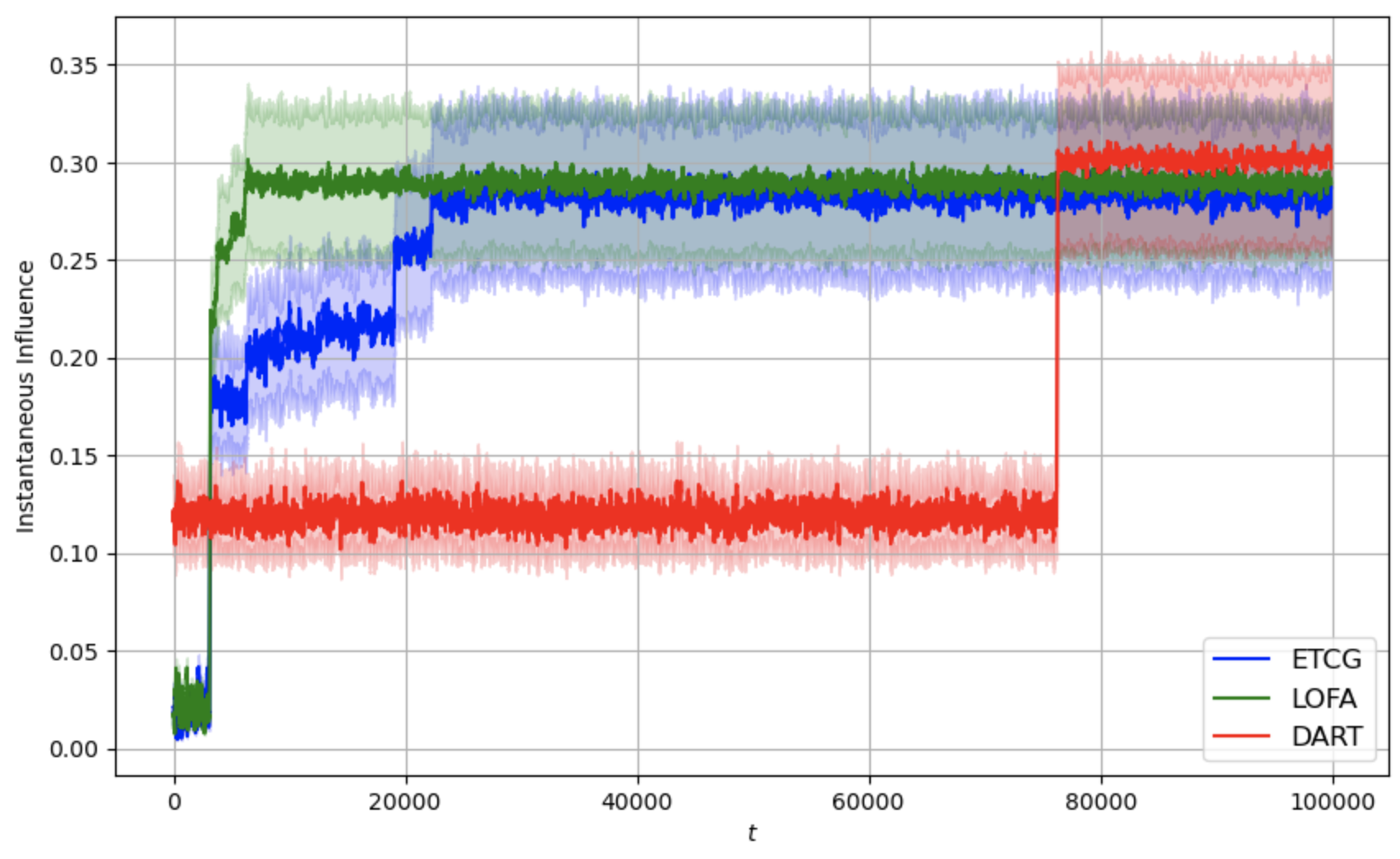
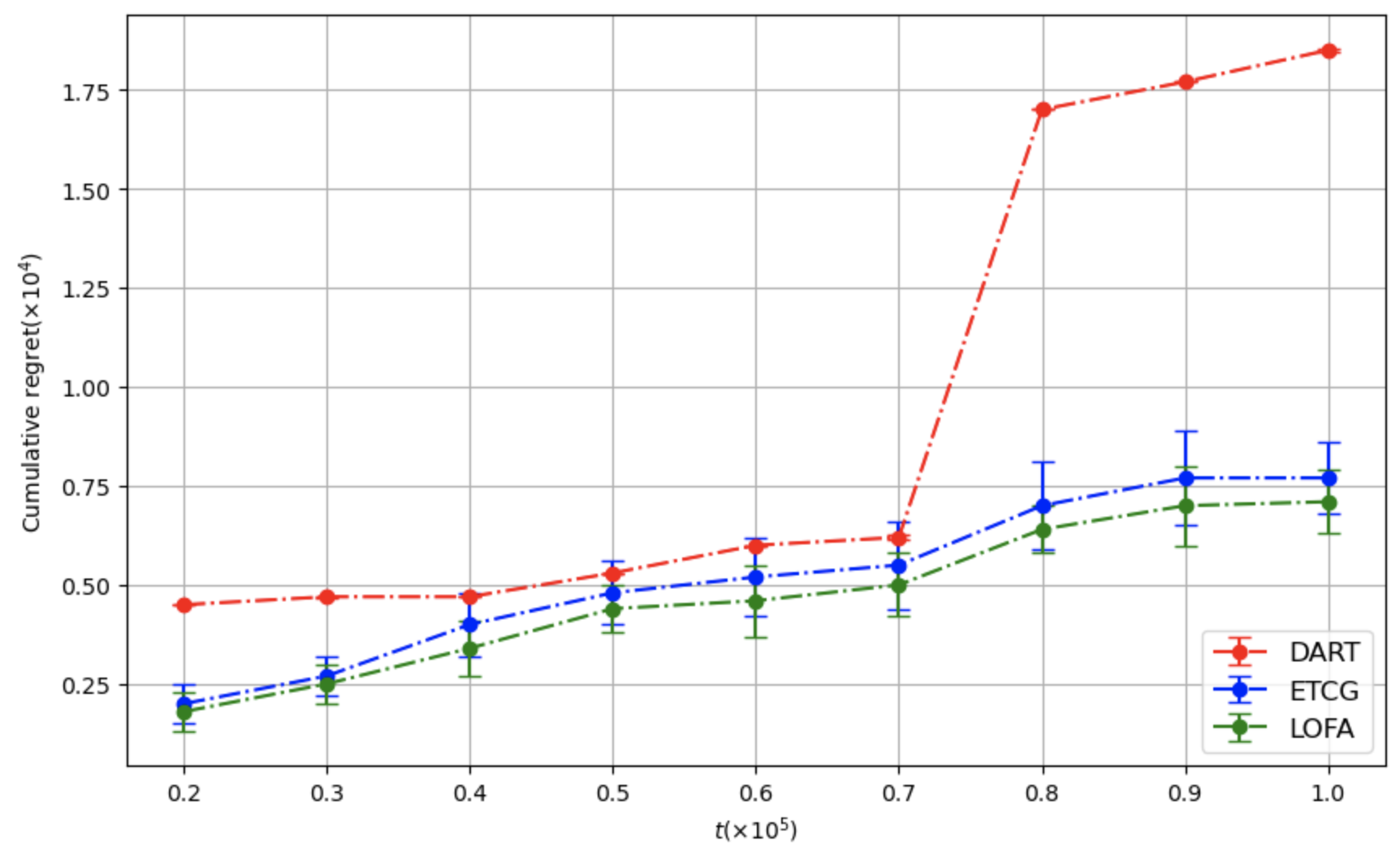
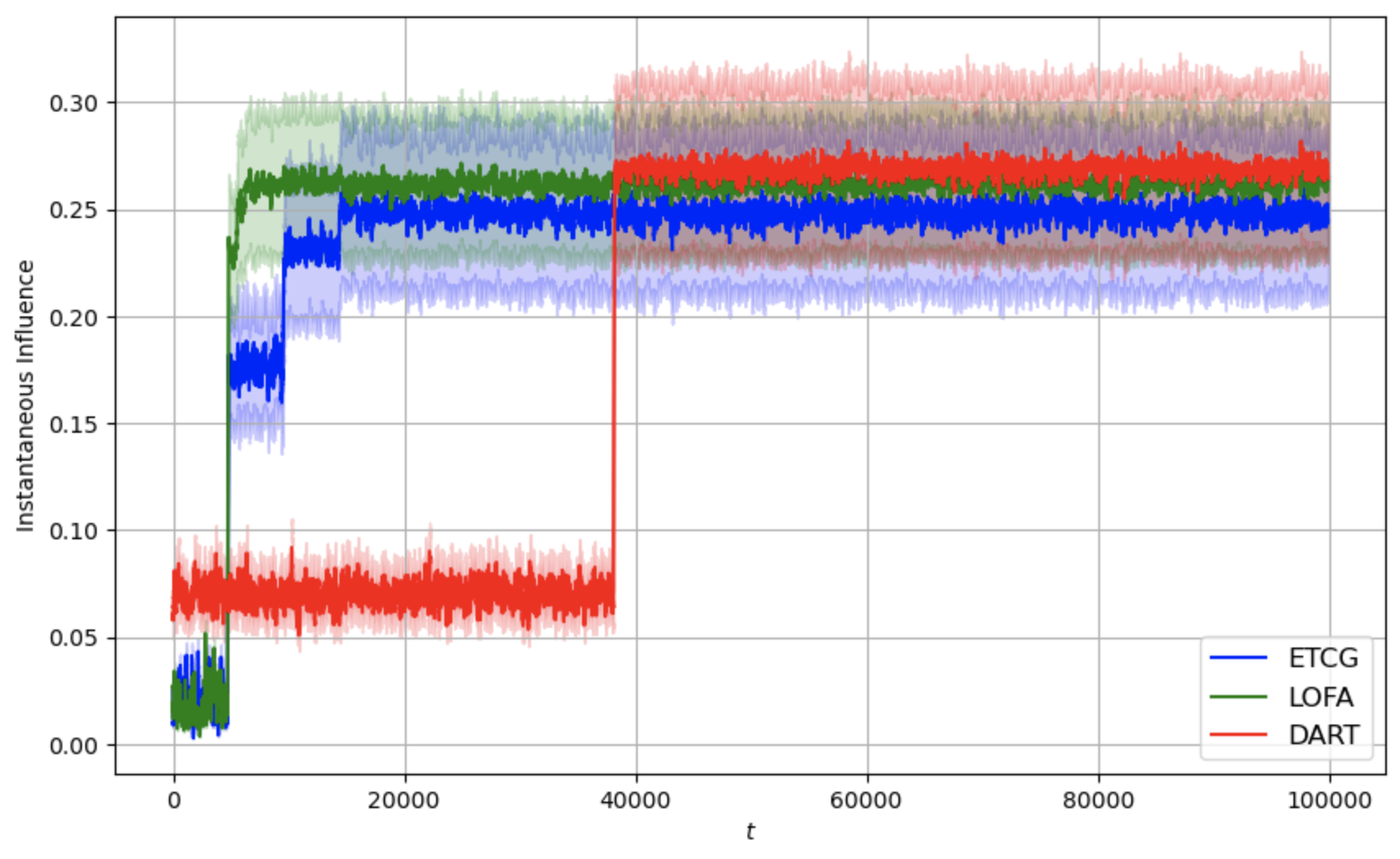
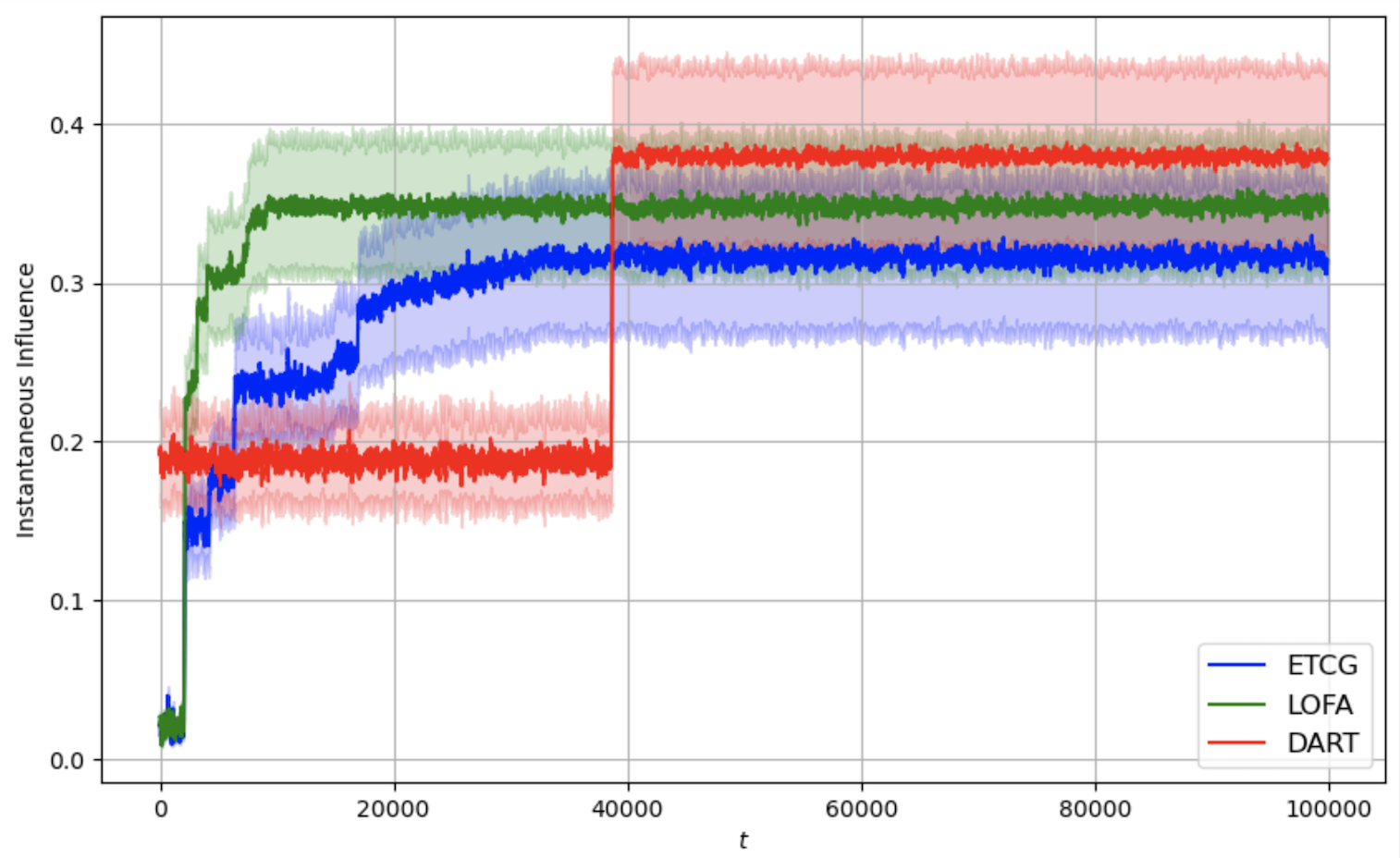
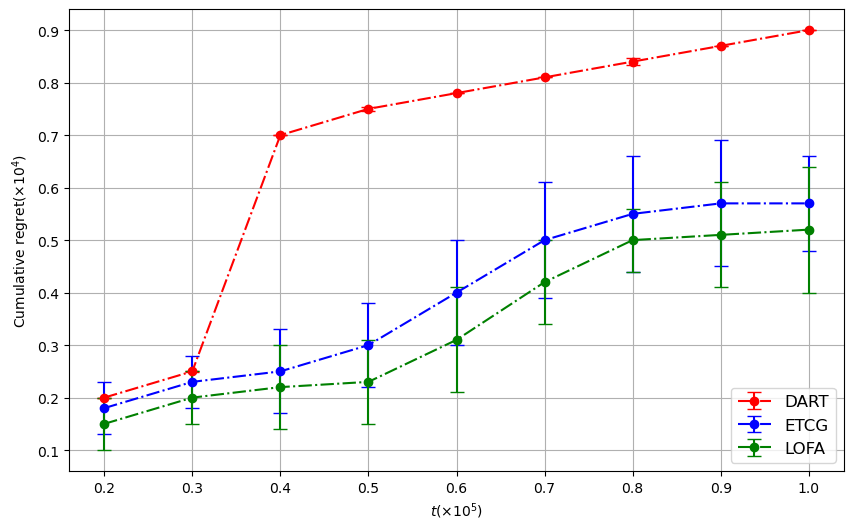
본 논문은 전체 피드백을 받는 온라인 설정 하의 영향력 최대화(IM) 문제를 위한 Lazy Online Forward Algorithm(LOFA)을 제안합니다. 실제 소셜 네트워크에서 LOFA가 다른 방법보다 경험적인 보상과 후회 측면에서 우수한 성능을 보이는 것을 실험으로 확인하였습니다.

구성

이 논문의 나머지 부분은 다음과 같이 구성됩니다. 2에서는 기본 개념과 관심 있는 문제를 정식화합니다. 3에서는 제안된 Online Lazy Forward Algorithm(LOFA)에 대해 논의하고, 4에서는 LOFA를 실제 소셜 네트워크에서 수행하여 경쟁 기준선과 비교한 성능을 보여줍니다. 마지막으로 5에서는 논문을 결론짓고 향후 방향성을 제시합니다.

기본 개념 및 문제 정식화

온라인 영향력 최대화(IM) 문제는 고전적인 IM 문제의 확장으로, 시간이 지남에 따라 소셜 네트워크에서 시드 노드를 순차적으로 선택하여 기대되는 영향력 확산을 최대로 하는 것이 목표입니다. 이 섹션에서는 논문에서 다루고자 하는 문제를 정식화합니다.

확산 모델 및 사회적 영향

확산 모델은 네트워크를 통해 영향력이 전파되는 과정을 설명합니다. 그 중 가장 광범위하게 연구된 것은 Independent Cascade(IC) 모델입니다. 다른 고전적인 모델로는 Linear Threshold 모델과 최근에 제안된 Pressure Threshold 모델이 있습니다.

본 논문에서는 IC 모델에 초점을 맞춥니다. IC 모델은 확률적 확산 프레임워크로서, 영향력이 이산 시간 단계를 통해 네트워크를 가로지르는 방식입니다. 유도 그래프 $`G = (V,E)`$에서 $`V`$는 노드 집합이고 $`E`$는 엣지 집합을 나타냅니다. 각 엣지 $(u, v) \in E$에는 영향력 확률 $p_{u,v} \in [0,1]$이 연결되어 있으며, 이는 노드 $u$가 노드 $v$를 성공적으로 활성화하는 가능성입니다.

시간 $t'=0$에서 시드 집합 $S \subseteq V$가 초기에 활성화됩니다. 각 후속 단계 $t' \geq 1$에서는 시간 $t'-1$에 활성화된 모든 노드 $u$가 현재 비활성 상태인 이웃 노드 $v$를 확률 $p_{u,v}$로 한 번만 활성화할 기회가 있습니다. 만약 활성화 성공 시, 노드 $v$는 시간 $t'$에 활성화되고 다음 라운드에서 이웃을 활성화하려고 합니다. 확산 과정은 더 이상 활성화가 발생하지 않는 시간 단계를 지나면 종료됩니다.

노드가 한 번 활성화되면, 그 후까지 계속 활성 상태로 유지되는 것이 중요합니다.

시드 집합 $S$의 영향력은 확산이 끝난 후 활성 노드의 수로 정의됩니다.

문제 진술

온라인 영향력 최대화(IM) 문제를 Independent Cascade(IC) 모델 하에서 이산 시간 단계에 걸쳐 시드 노드를 선택하는 순차 과정으로 정식화합니다. 각 엣지 $(u, v)$는 확률 $p_{u,v} \in [0,1]$로 활성화되며, 이 확률은 고정되어 있지만 학습자에게 알려져 있지 않습니다. 이러한 확률들은 라운드를 거치면서 변하지 않지만, 확산 결과는 확률적입니다. 이런 설정에서 엣지의 활성화 확률은 처음에는 알려져 있지 않고 밴딧 피드백을 통해 학습되어야 합니다.

주어진 시간 $T$ 동안 순차적인 의사결정 문제를 고려합니다. 각 라운드 $t \in {1, \dots, T}$에서 학습자는 제약 조건 $|S^t| \leq k$를 충족하는 서브셋 $S^t \subseteq \Omega$을 선택합니다.

라운드 $t$에서 서브셋 $S^t$을 선택한 후, 학습자는 영향력 $f_t(S^t)$을 관찰하며, 이는 네트워크에서 활성화 확산의 기대치를 측정하는 사회적 영향입니다. 액션 $S \subseteq V$의 수행은 시드 집합 $S$에서 시작되는 Independent Cascade 확산 과정의 한 실행을 의미합니다.

LOFA 알고리즘은 시간이 지남에 따라 서브셋 노드를 선택하고, 카디널리티 제약 조건을 만족할 때까지 그리디하게 추가한 후 해당 노드 집합을 활용하는 방법입니다.