신경망 체인과 이산 동역학 시스템
📝 원문 정보
- Title: Neural Chains and Discrete Dynamical Systems
- ArXiv ID: 2601.00473
- 발행일: 2026-01-01
- 저자: Sauro Succi, Abhisek Ganguly, Santosh Ansumali
📝 초록 (Abstract)
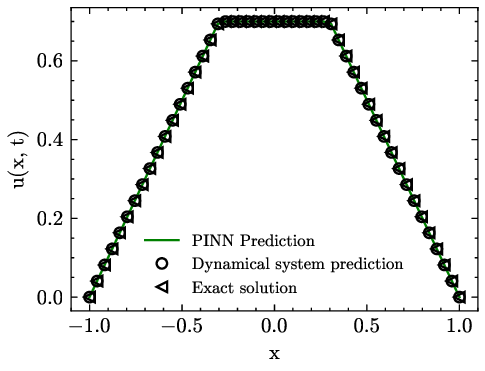
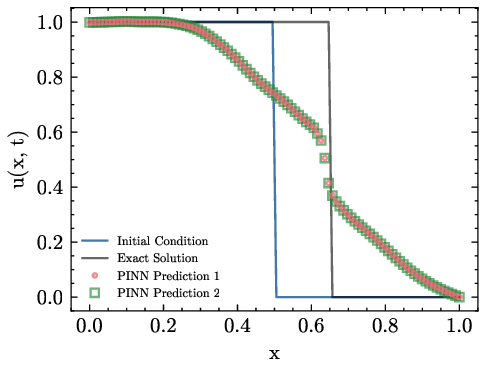
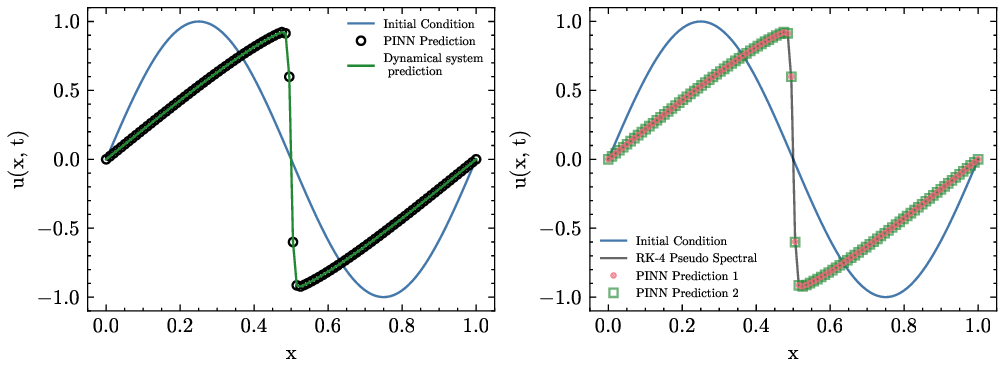
본 연구는 1차원 동적 문제에 대해 물리 기반 신경망(PINN)이 전통적인 유한 차분(FD) 방법과 비교했을 때, 매개변수 수가 크게 증가하고 물리적 투명성(설명 가능성)이 저하되는 이유를 밝힌다. 구체적으로, 행렬 공간에서 유일한 삼대각(tridiagonal) 형태가 존재함을 보이며, 이는 PINN이 무작위 매개변수 집합에 수렴하는 메커니즘을 설명한다. 이러한 대가로 학습 비용이 급증하고, FD 절차와는 달리 물리적 해석이 어려워진다. 다만, 연구 결과는 1차원 문제에 한정되므로, 고차원 문제에서는 PINN 및 머신러닝이 보다 유리한 전략을 제공할 가능성을 배제하지 않는다.💡 논문 핵심 해설 (Deep Analysis)
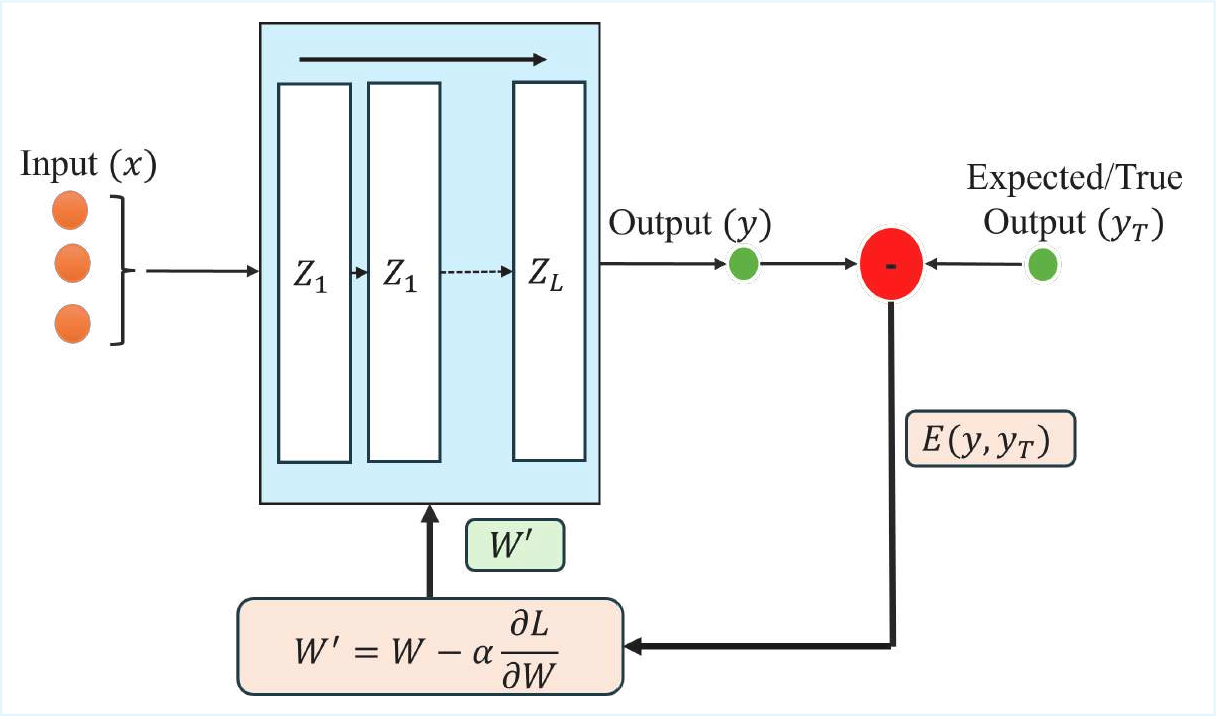
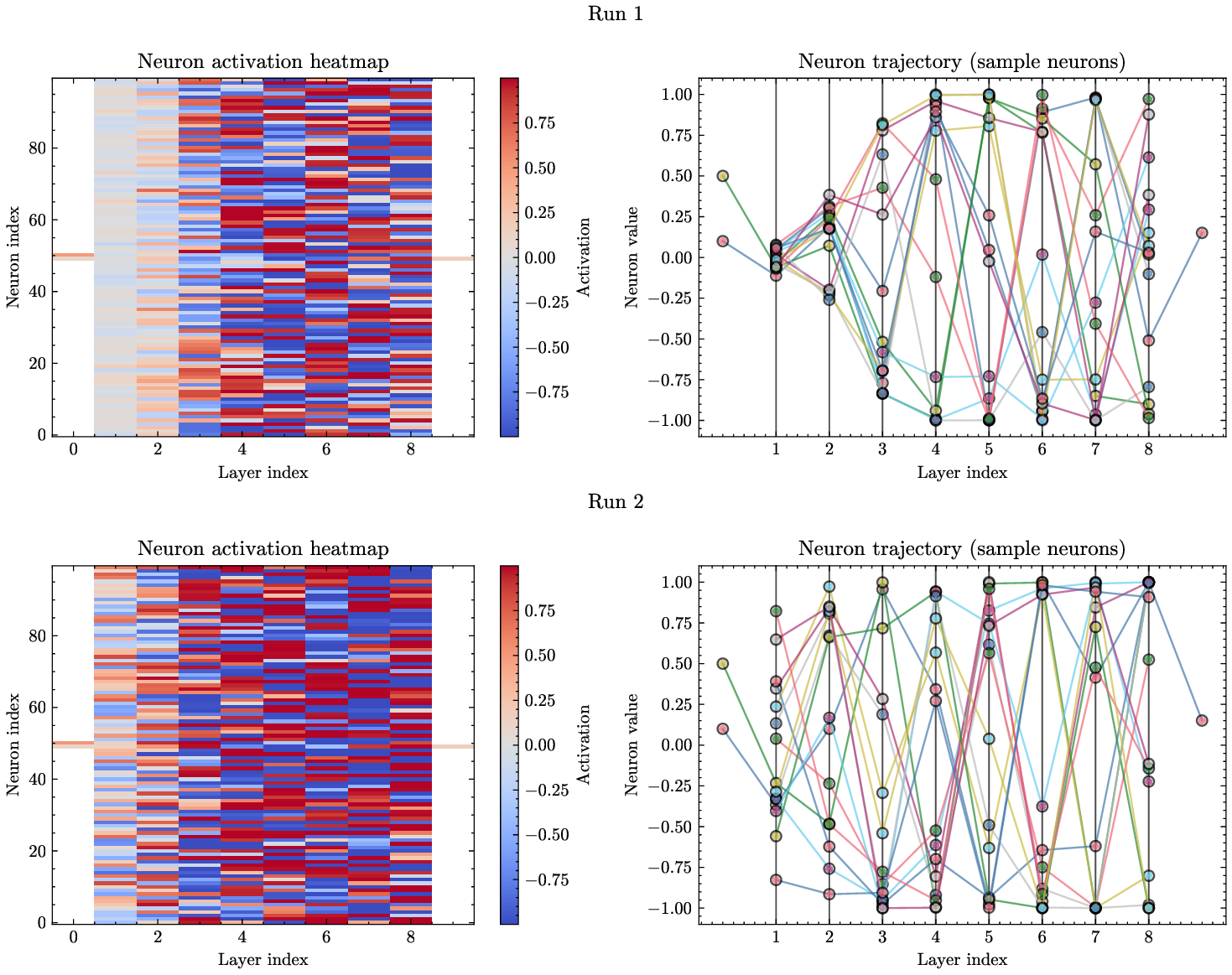
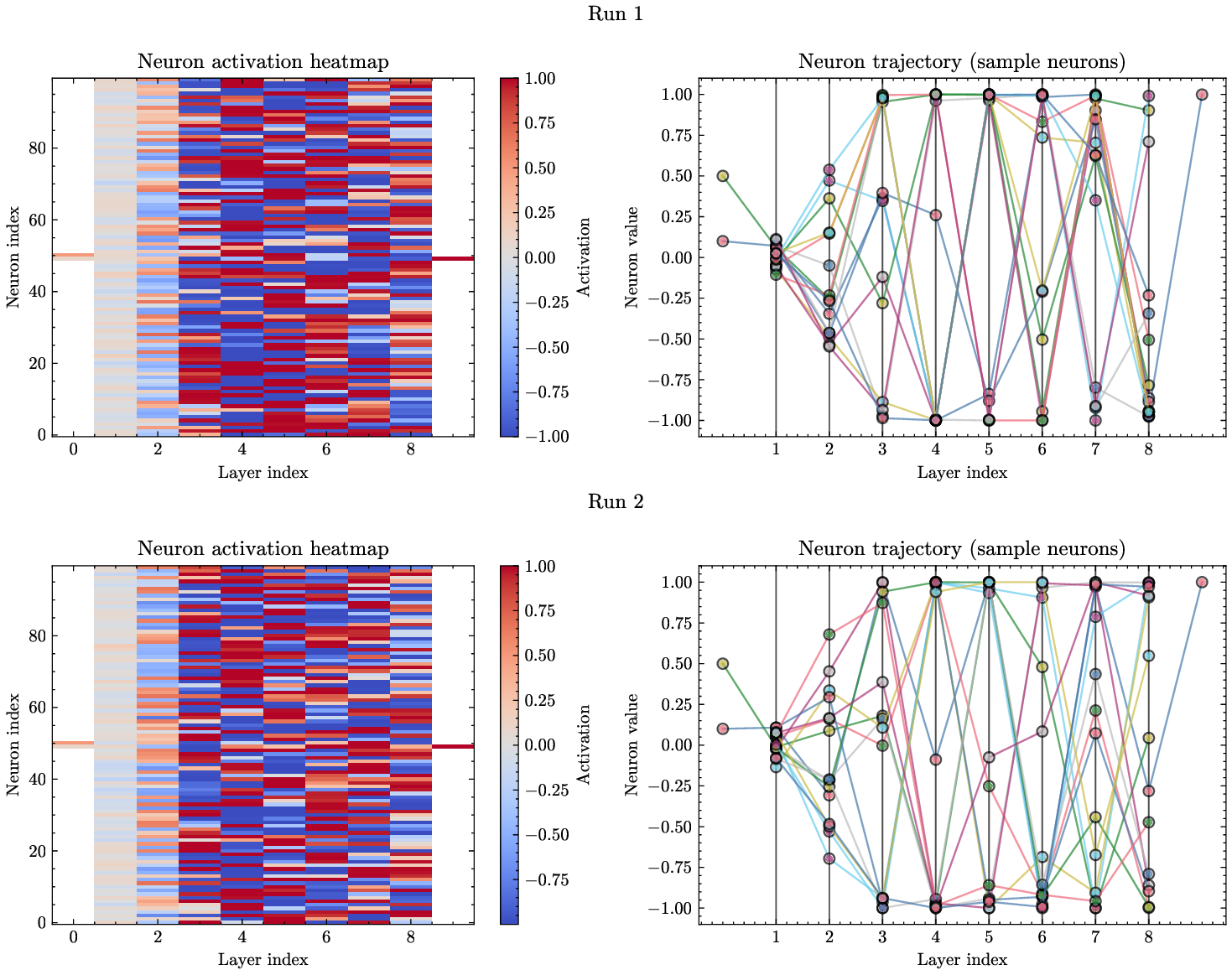
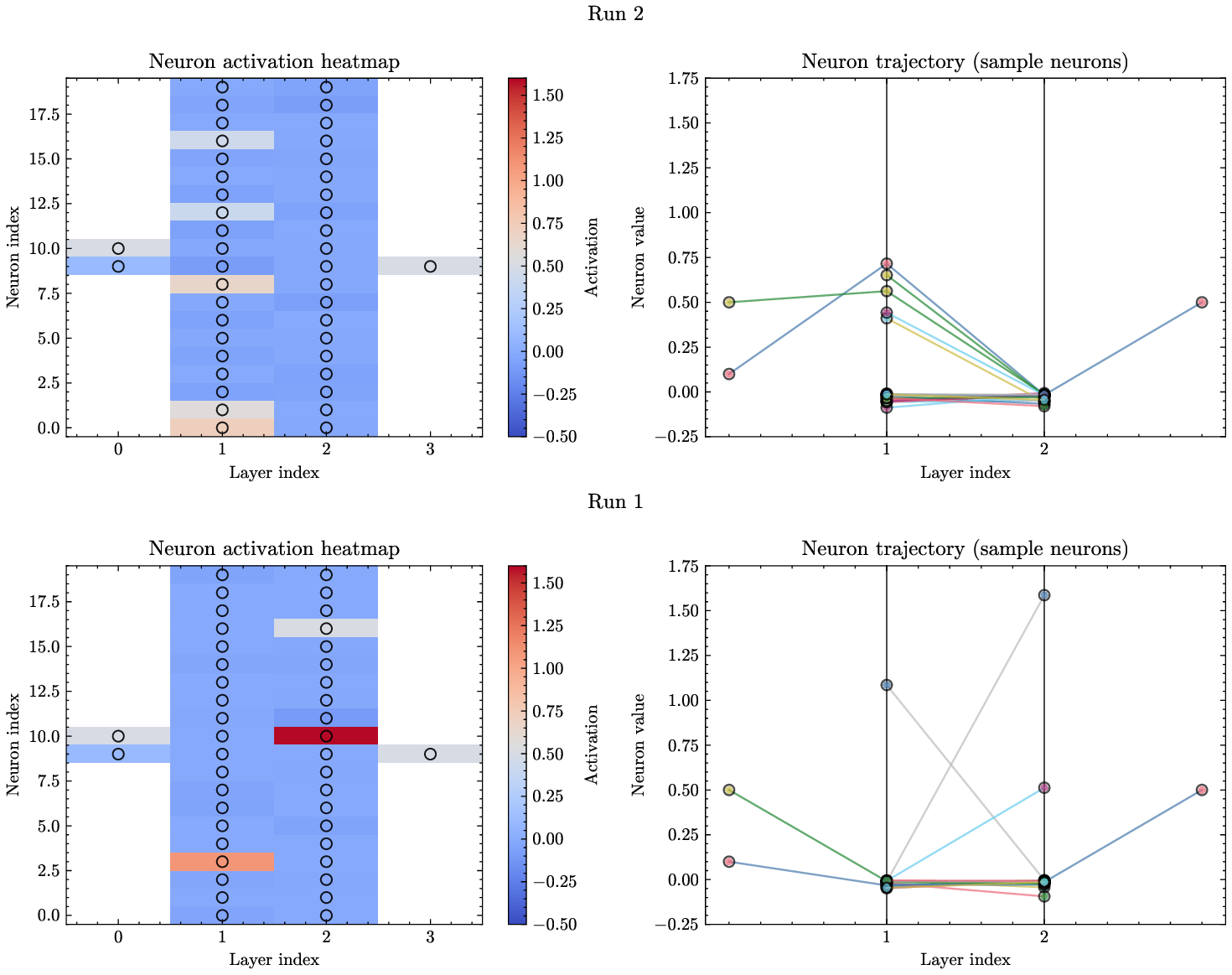
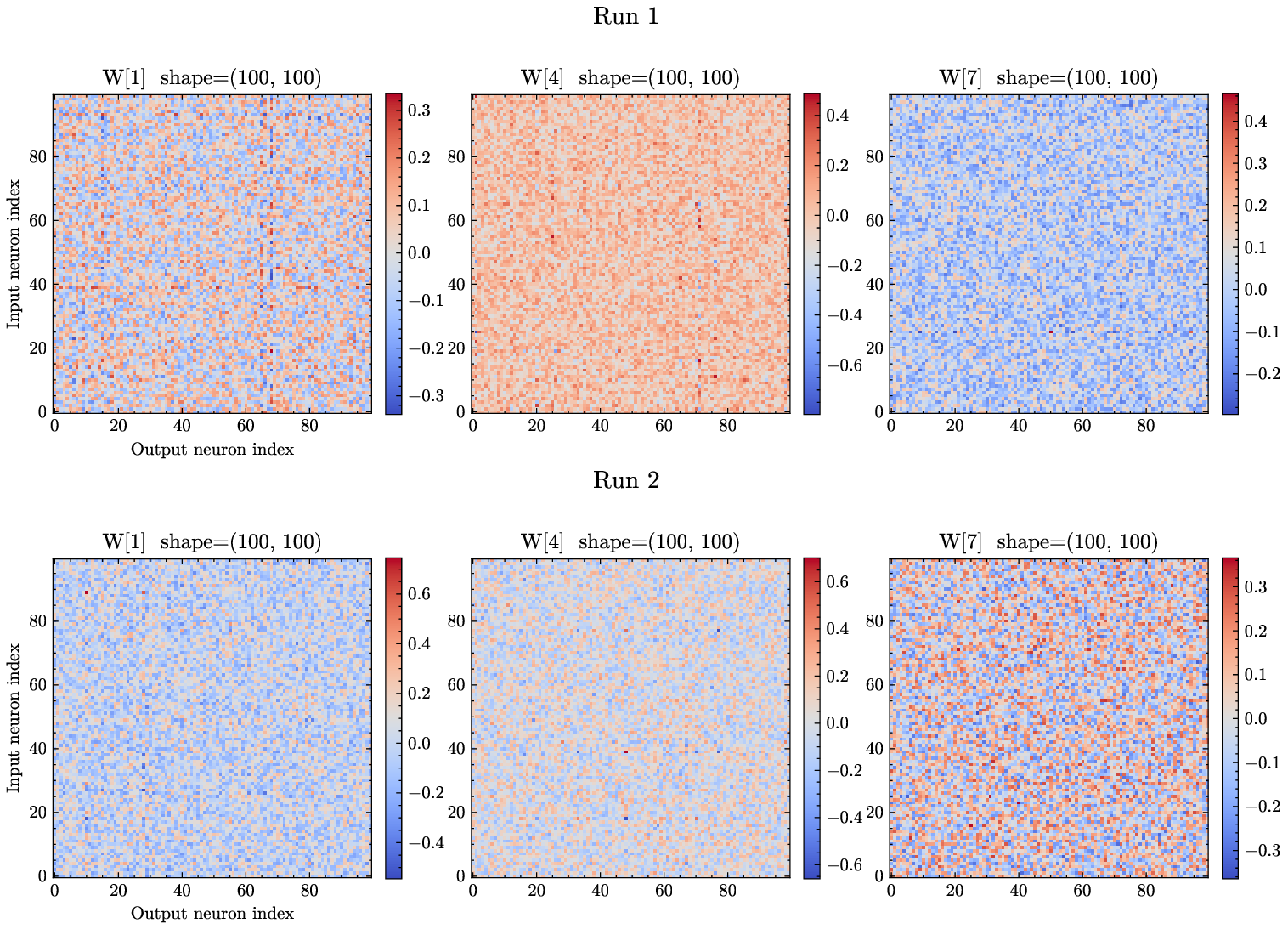
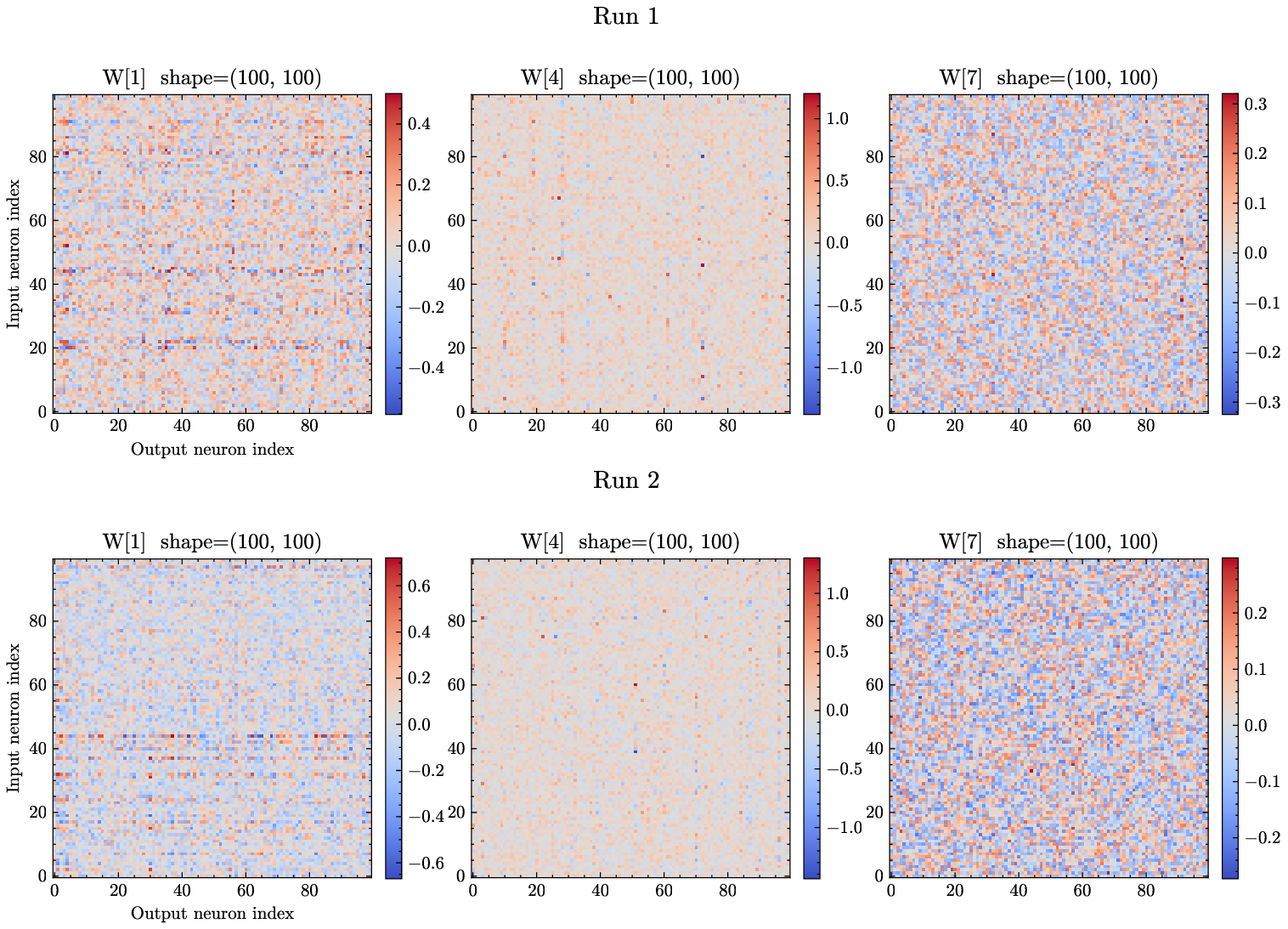
반면 PINN은 신경망 가중치를 최적화함으로써 미분 방정식의 잔차를 최소화한다. 신경망 자체는 완전 연결(fully‑connected) 혹은 복합적인 구조를 가지며, 가중치 매개변수는 일반적으로 수천에서 수백만 개에 달한다. 논문은 이러한 매개변수 공간이 “무작위 앙상블(random ensemble)”에 빠지기 쉬운 이유를, 삼대각 형태가 아닌 일반적인 밀집 행렬 형태로 표현되는 점에 기인한다고 설명한다. 즉, PINN이 찾는 최적해는 물리적으로 의미 있는 삼대각 구조를 강제하지 않으므로, 학습 과정에서 물리적 투명성(Explainability)이 크게 손상된다.
이러한 구조적 차이는 두 가지 실질적인 비용을 초래한다. 첫째, 매개변수 수가 급증함에 따라 학습에 필요한 데이터 양과 연산량이 크게 늘어난다. 특히 고정밀도 시뮬레이션을 위해 수천 번의 에포크를 수행해야 하는 경우, GPU 메모리와 전력 소모가 전통적인 FD 방법에 비해 수십 배 이상 증가한다. 둘째, 결과 해석이 어려워진다. FD는 각 격자점의 값이 직접 물리량에 대응하므로, 해석이 직관적이다. 반면 PINN은 가중치와 활성화 함수의 복합적인 조합으로 결과가 도출되므로, 왜 특정 해가 도출됐는지에 대한 설명이 복잡하고, 과학적 신뢰성을 확보하기 어렵다.
하지만 논문은 이 결론을 1차원 문제에 한정된다고 명시한다. 고차원(예: 3D 유체역학, 다변량 파동 방정식)에서는 격자 수가 기하급수적으로 증가해 FD의 메모리·시간 복잡도가 급격히 악화된다. 이때는 PINN이 “차원 저주(Curse of Dimensionality)”를 회피할 수 있는 잠재력을 가질 수 있다. 예를 들어, 신경망은 입력 차원을 자유롭게 확장하면서도 파라미터 수를 상대적으로 일정하게 유지할 수 있다. 또한 물리적 제약(예: 보존 법칙, 대칭성)을 네트워크 구조에 직접 인코딩함으로써, 무작위 앙상블에 빠지는 위험을 줄이고 설명 가능성을 향상시킬 수 있다.
결론적으로, 이 연구는 PINN이 1차원 동적 문제에서는 전통적인 FD에 비해 효율성·투명성 측면에서 열위에 있음을 명확히 밝히면서도, 고차원 복합 시스템에서는 아직 검증되지 않은 가능성을 남겨두고 있다. 향후 연구는 (1) 신경망 구조에 삼대각성 혹은 희소성을 강제하는 정규화 기법, (2) 물리 기반 손실 함수와 데이터 기반 손실 함수의 균형을 최적화하는 하이브리드 접근법, (3) 고차원 문제에 대한 벤치마크를 구축해 PINN과 전통적 수치법의 성능을 정량적으로 비교하는 작업이 필요하다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리