/>

최근 생성 모델의 발전은 시각적 콘텐츠 창작 분야를 크게 진보시켰으며, 예술 디자인과 엔터테인먼트부터 의료 영상 및 가상 현실에 이르기까지 다양한 응용 분야에서 활용되고 있습니다. 최신 확산 모델과 흐름 기반 접근법은 높은 품질의 이미지와 비디오 생성에 대한 뛰어난 정확도를 달성하였습니다.

대형 언어 모델에서는 강화 학습이 인간 선호와의 정합성을 증진하는 데 효과적이었습니다. Proximal Policy Optimization (PPO), Direct Policy Optimization (DPO), 그리고 Group Relative Policy Optimization (GRPO) 등은 이에 대한 좋은 예입니다. 따라서 강화학습에서 인류 피드백 (RLHF)이 시각적 생성의 후 훈련 단계에서 활용되었습니다. GRPO는 가치 네트워크를 제거하여 군 내 상대 보상을 사용해 직접적으로 이점을 계산함으로써 구조를 단순화합니다. 최근 연구들은 이를 확률론적 미분 방정식 (SDE)을 사용한 흐름 모델에 통합하였습니다. 샘플링 효율성을 높이기 위해 일부 방법은 SDE 샘플링과 ODE 샘플링의 혼합을 도입하였으며, 다른 방법들은 더 적은 샘플링 단계를 위한 트리 기반 구조를 제안하였습니다.

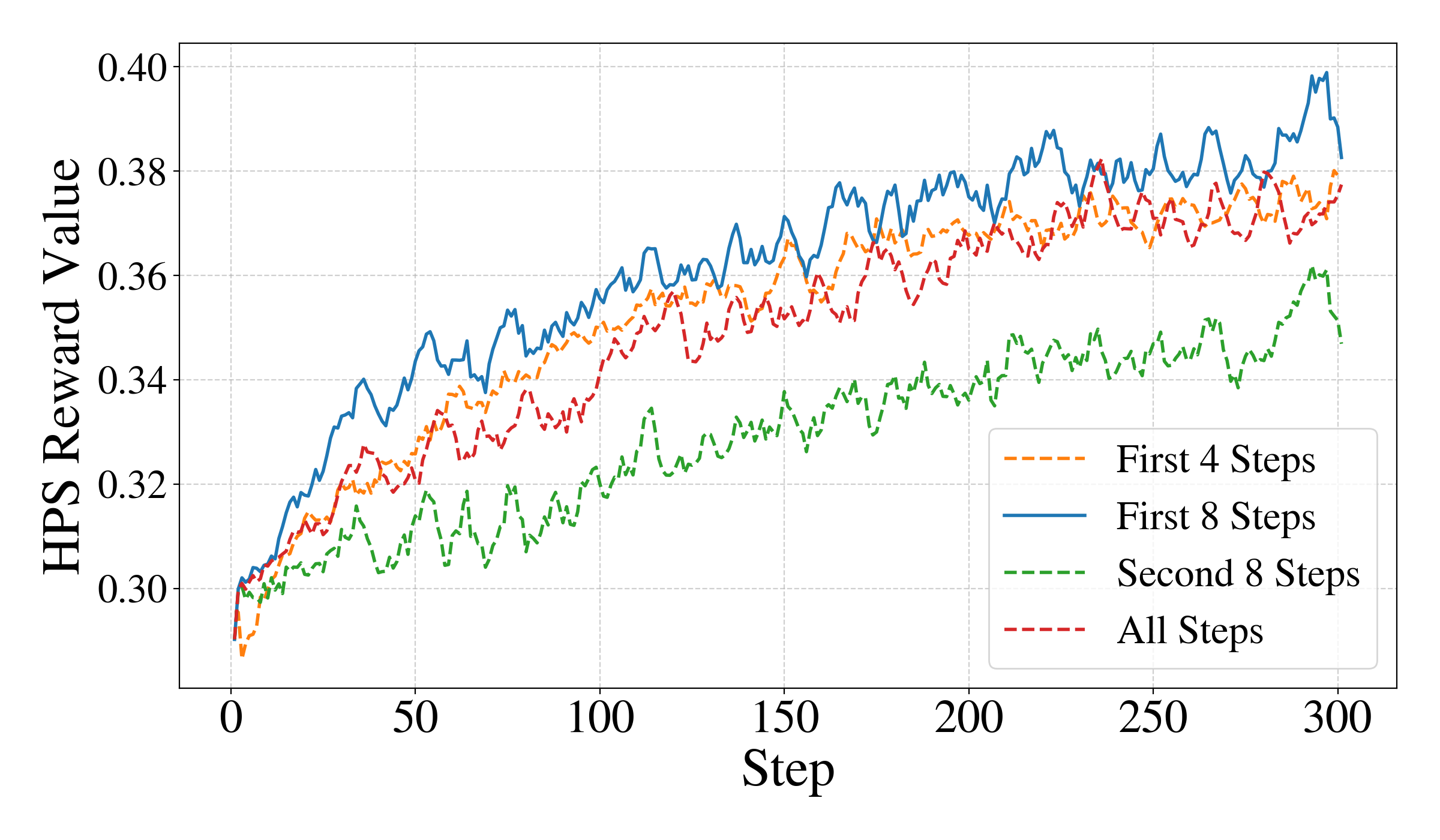
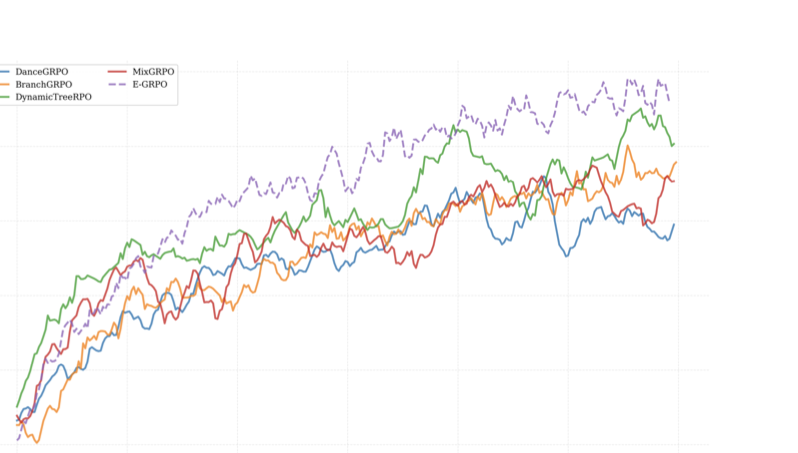
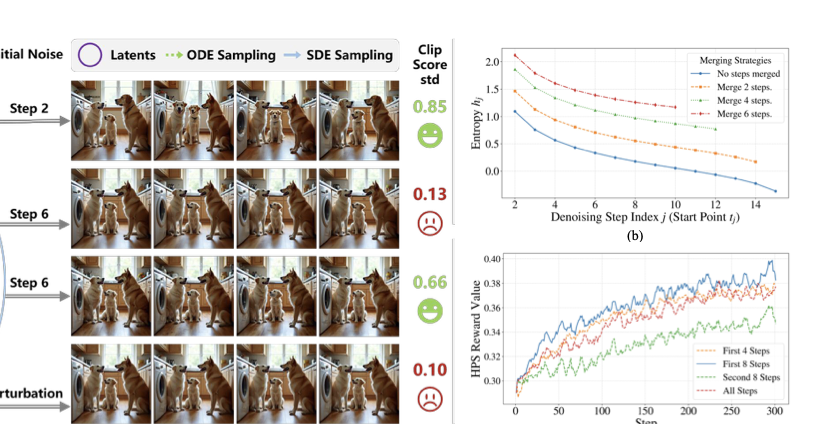
그럼에도 불구하고 현재 GRPO 기반 방법은 여러 해노이스 단계에 걸친 정책 최적화를 적용하여 희박하고 모호한 보상 신호를 생성함으로써 효과적인 정합을 방해합니다. 우리는 높은 엔트로피 단계만이 훈련 동력학에 의미있게 기여한다는 것을 관찰했습니다. Figure 1 (b)에서 볼 수 있듯이, 더 높은 잡음 수준의 타임스텝에서는 SDE를 통해 확률론적 탐색을 수행하며 엔트로피가 크게 증가합니다. 다양한 상황 하에서 생성된 이미지를 시각화하였으며, 높은 엔트로피 단계는 다양하고 구별 가능한 보상 변동성을 가지는 이미지들을 생성하지만, 낮은 엔트로피 단계에서는 거의 차이가 없는 보상 변화를 보여줍니다. 이 현상은 보상 모델들이 낮은 엔트로피 환경에서 미세한 경로 편차를 구별하기 어려움을 시사합니다. 더불어, 우리는 GRPO와 SDE 샘플링을 네 가지 설정에 적용하였습니다: (i) 처음 4 단계, (ii) 처음 8 단계, (iii) 두 번째 8 단계, 그리고 (iv) 전체 16 단계. 특히 첫 번째 반의 단계에서 최적화가 전체 단계보다 더 좋은 성능을 보여주며, 이는 두 번째 반의 단계들이 대부분 정보성이 낮다는 것을 시사합니다.

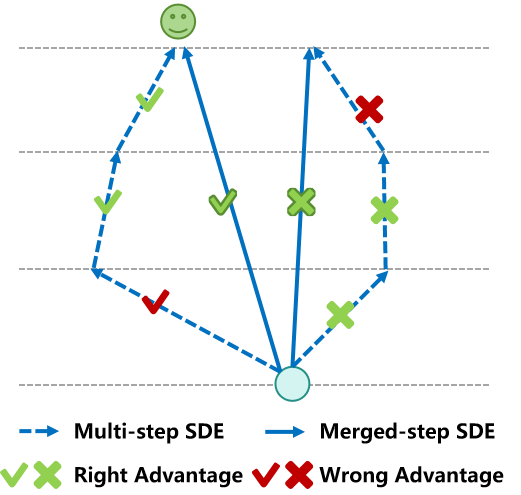
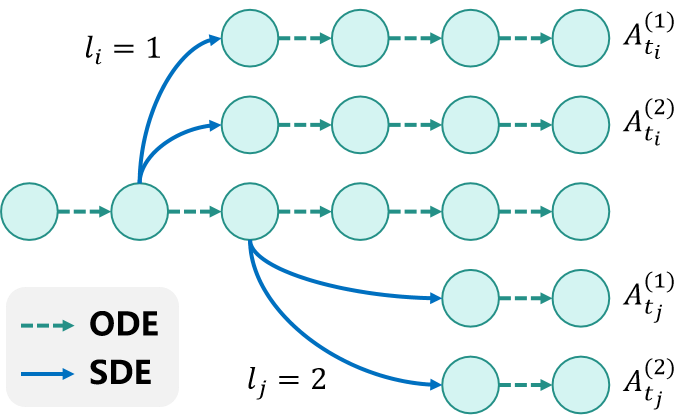
이 한계를 극복하기 위해 우리는 E-GRPO를 제안합니다. 이는 GRPO 훈련 중 효과적인 탐색을 위한 엔트로피 기반 SDE 샘플링 전략입니다. 직관적으로 다중 연속 SDE 샘플링을 사용하여 탐색 영역을 확장할 수 있지만, 이 방법은 누적 확률론성을 가져와 각 단계에서 보상 귀속이 모호해지게 합니다. 따라서 우리는 여러 낮은 엔트로피 SDE 단계를 하나의 효과적인 SDE 단계로 통합하고 나머지 단계들을 결정론적 ODE 샘플링으로 유지하여 정보성이 있는 곳에서만 높은 엔트로피 탐색을 보장합니다. 이를 기반으로, 우리는 동일한 병합된 SDE 단계를 공유하는 샘플들 내에서 군 상대 이점을 계산하기 위한 다중 단계 그룹 정규화 이점을 도입하였습니다. 이 메커니즘은 밀도가 높고 신뢰할 수 있는 보상 신호를 제공하여 생성 경로를 인간 선호와 더욱 정합되게 만듭니다.

우리는 싱글 보상 설정과 멀티 보상 설정, 그리고 in-domain 및 out-of-domain 평가 매트릭스에 대한 실험을 수행하였습니다. 실험 결과는 우리의 방법의 효과성과 효율성을 입증합니다. 주요 기여를 다음과 같이 요약할 수 있습니다:

1. GRPO 훈련 과정에서 해노이스 단계들의 엔트로피에 대한 포괄적인 분석을 제공하며, 효과적인 정합은 높은 엔트로피 단계만 최적화함으로써 달성될 수 있음을 밝혔습니다.
2. E-GRPO는 GRPO 훈련 중 낮은 엔트로피 단계를 하나의 높은 엔트로피 SDE 단계로 통합하여 의미있는 탐색을 확장하고 보상 귀속 모호성을 해소하는 엔트로피 기반 SDE 샘플링 전략입니다.
3. 싱글 보상 및 멀티 보상 설정에서 광범위한 실험을 수행하여 E-GRPO가 항상 이전 방법보다 우수한 성능을 보여주며, 엔트로피 기반의 정확하고 안정적인 확률론적 최적화 효과를 입증하였습니다.

관련 연구

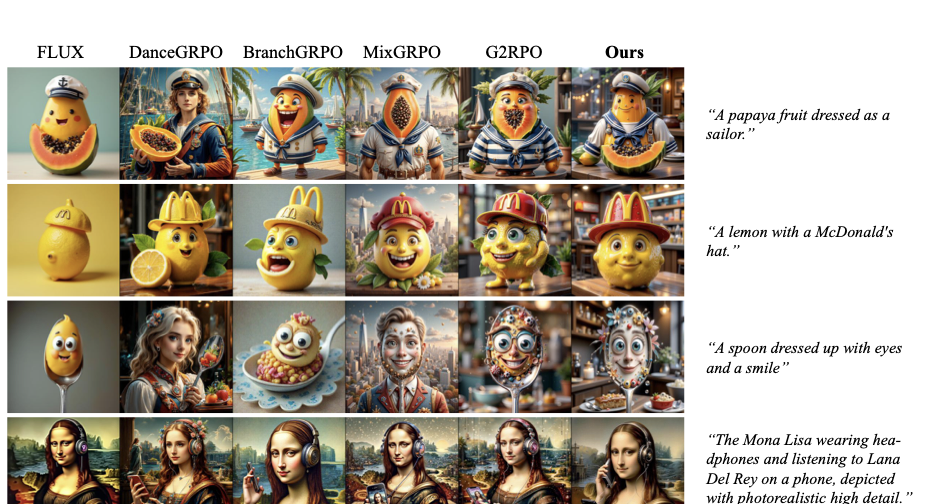
이미지 생성을 위한 강화 학습 정합. 인류 피드백에서 강화 학습 (RLHF) 및 검증 가능한 보상과 함께 강화 학습 (RLVR)은 대형 언어 모델 (LLMs)과 인간 선호의 정합성에 대한 강력한 패러다임을 제공하였습니다. 초기 프레임워크는 Proximal Policy Optimization (PPO)를 기반으로 가치 모델을 사용하여 정책 업데이트를 안내하였으나, 최근 Group Relative Policy Optimization (GRPO)와 같은 접근법은 절대 보상 대신 상대 군별 비교를 활용함으로써 더 큰 안정성과 효율성을 달성하였습니다. 이러한 언어 모델의 정합성 향상에 대한 연구는 시각적 생성 모델을 인간 선호와 정합시키기 위한 강화 학습 기법 전이에 대한 관심을 더욱 높였습니다. 시각적 생성 분야에서는 확산 및 흐름 일치 모델이 반복적인 해노이스 과정을 통해 강력한 생성 능력을 입증하였습니다. 인간 피드백과의 정합성을 개선하기 위해 최근 연구들은 이러한 모델에 RLHF를 적용하였습니다. Diffusion-DPO와 D3PO는 Direct Preference Optimization (DPO)를 확산 모델로 확장하였으나, 이 방법들은 훈련 과정에서 새로운 샘플을 생성하지 않아 분포 변화의 문제를 겪었습니다. DanceGRPO 및 Flow-GRPO는 결정론적 ODE 기반 샘플링을 확률론적 SDE 경로로 재구성하여 시각 도메인에서 GRPO 스타일의 정책 업데이트가 가능하도록 하였습니다. 이를 기반으로 Granular-GRPO는 더 정밀하고 밀도 높은 신용 할당을 위해 해노이스 단계의 세분화를 개선했으며, TempFlow-GRPO는 일정한 시간스텝에 걸친 최적화 한계를 완화하기 위한 시점 인식 가중치를 도입하였습니다. MixGRPO는 하이브리드 ODE-SDE 샘플링 메커니즘을 통해 훈련 효율성을 개선했으며, BranchGRPO는 분기 롤아웃 및 구조적 가지치기를 통해 탐색 효율성을 높였습니다. 그러나 이러한 발전에도 불구하고 기존의 흐름 모델에 대한 GRPO 프레임워크는 해노이스 과정에서 탐색 잠재력의 이질성을 무시하고 모든 시간스텝에 걸친 균일한 최적화를 적용하여 희박하거나 노이지 보상 신호 문제를 겪습니다. 본 연구에서는 각 단계별 엔트로피를 탐색 능력을 측정하는 지표로 활용하여 높은 엔트로피 단계에서 최적화를 통해 안정성과 효율성을 개선합니다.

엔트로피 기반 탐색 및 정합. 초기 강화 학습 연구는 효과적인 탐사를 촉진하는 메커니즘으로 엔트로피의 중요성을 인식하였습니다. 특히, 정책 엔트로피 정규화와 같은 전략은 다양하고 안정적인 학습을 촉진하기 위해 널리 사용되었습니다. 예를 들어 Soft Actor-Critic (SAC)는 기대 보상과 함께 정책 엔트로피를 최대화하여 더 강건하고 샘플 효율적인 탐사를 실현합니다. 최근에는 엔트로피에 대한 통찰이 대형 언어 모델(Large Language Models, LLMs)의 추론을 위한 강화 학습에서 활용되었습니다. 연구 결과, 소수의 높은 엔트로피 토큰이 정책 개선을 주도함으로써 토큰 수준의 불확실성이 탐사를 안내하는 데 중요하다는 것을 보여주었습니다. 이에 대한 추가적인 연구에서는 엔트로피를 탐색 동력학을 이해하는 렌즈로 체계화하여, 높은 엔트로피 영역이 학습에 가장 정보성이 있는 중요한 결정 지점임을 입증하였습니다. 이러한 발견에 착안해 우리는 유사한 엔트로피 기반 패턴이 흐름 일치 모델에서도 나타나는지 조사하였고, 인간 선호와의 정합성을 더욱 효율적이고 안정적으로 만드는 엔트로피 기반 GRPO 프레임워크를 제안하였습니다.

방법

개요

강화 학습에서 탐색을 가능하게 하기 위해 흐름 기반 Group Relative Policy Optimization (GRPO)은 결정론적 ODE 샘플링:

\begin{equation}
\mathrm{d}\mathbf{x}_t = \mathbf{v}_\theta(\mathbf{x}_t, t) \, \mathrm{d}t
\end{equation}

를 다음과 같은 동등한 SDE로 변환합니다:

\begin{align}
\mathbf{x}_{t+\Delta t} = & \mathbf{x}_t + \left[ \mathbf{v}_\theta(\mathbf{x}_t, t) + \frac{\sigma_t^2}{2t} \big(\mathbf{x}_t + (1-t)\mathbf{v}_\theta(\mathbf{x}_t, t)\big) \right] \Delta t \nonumber
\\ &+ \sigma_t \sqrt{\Delta t} \, \boldsymbol{\epsilon},
\end{align}

여기서 $`\boldsymbol{\epsilon} \sim \mathcal{N}(0, I)`$이고, $`\sigma_t = a \sqrt{\frac{t}{1-t}}`$. SDE 샘플링을 통해 흐름 일치 모델에 온라인 강화 학습을 통합하여 역방향 샘플링을 상태 $`\mathbf{s}_t = (\mathbf{x}_t, t)`$, 행동 $`\mathbf{a}_t = \mathbf{x}_{t-1} \sim \pi_\theta(\cdot | \mathbf{s}_t)`$, 그리고 프롬프트 $`c`$에 대한 종료 보상 $`R(\mathbf{x}_0, c)`$를 갖는 Markov Decision Process (MDP)로 표현합니다. 정책은 다음과 같이 최적화됩니다:

\begin{equation}
J_{\text{Flow-GRPO}}(\theta) = \mathbb{E}_{c \sim \mathcal{C},\ \{\mathbf{x}^{(i)}\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|c)} \left[ f(r, A, \theta, \epsilon) \right]. \nonumber
\end{equation}

자르기된 서로대상 함수 $`f(r, A, \theta, \epsilon)`$는 다음과 같이 정의됩니다:

\begin{align}
\frac{1}{G} \sum_{i=1}^G \frac{1}{T} \sum_{t=0}^{T-1} \Big[ \min\!\big(r_t^{(i)} A^{(i)}, \text{clip}(r_t^{(i)}, 1-\epsilon, 1+\epsilon) A^{(i)}\big) \notag 
\Big], \nonumber
\end{align}

여기서 $`r_t^{(i)}(\theta) = \frac{p_\theta(\mathbf{x}_{t-1}^{(i)} \mid \mathbf{x}_t^{(i)}, c)}{p_{\theta_{\text{old}}}(\mathbf{x}_{t-1}^{(i)} \mid \mathbf{x}_t^{(i)}, c)}`$, 그리고 $`p_\theta(\mathbf{x}_{t-1}^{(i)} \mid \mathbf{x}_t^{(i)}, c)`$는 타임스텝 $`t-1`$에서 출력 $`\mathbf{x}^{(i)}`$에 대한 정책 함수입니다. 군 정규화 이점 $`A^{(i)}`$는 다음과 같이 표현됩니다:

\begin{equation}
A^{(i)} = \frac{R(\mathbf{x}_0^{(i)}, c) - \text{mean}\{R(\mathbf{x}_0^{(j)}, c)\}_{j=1}^G}{\text{std}\{R(\mathbf{x}_0^{(j)}, c)\}_{j=1}^G}.
\end{equation}

이전 방법의 관행에 따라 목적 함수에서는 KL 정규화 항을 생략합니다.

엔트로피 분석

흐름 기반 Group Relative Policy Optimization에서는 역방향 SDE 샘플링 과정을 Markov Decision Process (MDP)로 표현합니다. 역방향 SDE 단계의 엔트로피를 파악하기 위해 주어진 전방향 SDE로부터 베이즈 정리를 적용합니다. 전방향 SDE는 다음과 같습니다:

\begin{align}
\mathbf{x}_{t+\Delta t} = \mathbf{x}_t + \mu_{\theta}(\mathbf{x}_t, t) \Delta t + \sigma_t \sqrt{\Delta t}\boldsymbol{\epsilon}, \label{eq:forward SDE}
\end{align}

여기서 $`\boldsymbol{\epsilon} \sim \mathcal{N}(0, I)`$는 확률론성을 주입하며, 유동 항은 다음과 같습니다:

\begin{align}
\mu_{\theta}(\mathbf{x}_t, t) = \mathbf{v}_\theta(\mathbf{x}_t, t) + \frac{\sigma_t^2}{2t} \big(\mathbf{x}_t + (1-t)\mathbf{v}_\theta(\mathbf{x}_t, t)\big). \nonumber
\end{align}

전방향 SDE의 전이 확률은 가우시안 분포입니다:

\begin{align}
p_{\text{f}}(\mathbf{x}_{t+\Delta t} \mid \mathbf{x}_t) = \mathcal{N}\left( \mathbf{x}_{t+\Delta t} \mid \mathbf{x}_t + \mu_{\theta}(\mathbf{x}_t, t) \Delta t,\ \sigma_t^2 \Delta t \, I \right). \nonumber
\end{align}

베이즈 정리를 통한 역방향 SDE. 역방향 전이 확률 $`p_{\text{r}}(\mathbf{x}_t \mid \mathbf{x}_{t+\Delta t})`$, GRPO에서의 정책 $`\pi_\theta`$를 나타내는 이전 단계에서는 베이즈 정리를 사용하여 도출됩니다:

\begin{align}
p_{\text{r}}(\mathbf{x}_t \mid \mathbf{x}_{t+\Delta t}) = \frac{p_{\text{f}}(\mathbf{x}_{t+\Delta t} \mid \mathbf{x}_t) \, p(\mathbf{x}_t)}{p(\mathbf{x}_{t+\Delta t})}. \nonumber
\end{align}

가우시안 프로세스에 대한 역방향 전이 또한 가우시안 분포입니다:

\begin{align}
p_{\text{r}}(\mathbf{x}_t \mid \mathbf{x}_{t+\Delta t}) = \mathcal{N}\left( \mathbf{x}_t \mid \tilde{\mu}_{\theta}(\mathbf{x}_{t+\Delta t}, t),\ \tilde{\sigma}_t^2 \Delta t \, I \right), \nonumber
\end{align}

여기서 $`\tilde{\mu}_{\theta}`$는 역방향 유동이며 $`\tilde{\sigma}_t`$는 역방향 확산 계수입니다. 선형 가우시안 SDE에서는 프로세스가 시간 반전 가능할 때 양 방향의 확산 계수가 동일하여 $`\tilde{\sigma}_t = \sigma_t`$. 역방향 유동 $`\tilde{\mu}_{\theta}`$에 대해 전방향 전이 확률의 로그는 다음과 같습니다:

\begin{align}
\log p_{\text{f}} = & -\frac{1}{2} \log \det(2\pi \sigma_t^2 \Delta t I) \nonumber \\
& -\frac{1}{2\sigma_t^2 \Delta t} \left\| \mathbf{x}_{t+\Delta t} - \mathbf{x}_t - \mu_{\theta}(\mathbf{x}_t, t) \Delta t \right\|^2 \nonumber
\end{align}

$`\mathbf{x}_t`$에 대해 미분을 취하면 역방향 유동은 다음과 같이 표현됩니다:

\begin{align}
\tilde{\mu}_{\theta}(\mathbf{x}_{t+\Delta t}, t) = \mathbf{x}_{t+\Delta t} - \mu_{\theta}(\mathbf{x}_t, t) \Delta t + \sigma_t^2 \Delta t \, \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t). \nonumber
\end{align}

역방향 SDE 단계의 엔트로피. 다변량 가우시안 분포 $`\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})`$의 엔트로피는 다음과 같습니다:

\begin{align}
h(\mathbf{y}) = \frac{d}{2} \log\left( (2\pi e)^d \det(\boldsymbol{\Sigma}) \right)
\end{align}

여기서 $`d`$는